1.9. Высшая категория сингоний

Кубическая сингония

Формулы и виды симметрии:

1) 3L₄ 4L₃ 6L₂ 9PC – планальный вид симметрии;

2) 3L₄ 4L₃ 6L₂ – аксиальный;

3) 4L₃ 6L₂ 6P – планальный;

4) 4L₃ 3L₂ 3PC – центральный;

5) 4L₃ 3L₂ – примитивный.

Простые формы: в кубической сингонии существует 5 основных простых форм и 10 производных.

Основные простые формы (рис.4.1-4.15):

1) кубический тетраэдр – 4 равные грани в форме правильного треугольника, из которого каждые 3 грани пересекаются в одной точке (рис.4.1);

2) октаэдр – 8 граней в форме правильных треугольников (рис.4.2);

3) гексаэдр (куб) – 6 граней в форме квадратов (рис.4.3);

4) ромбо-додекаэдр – 12 граней в форме ромбов (рис.4.4);

5) пентагон-додекаэдр – 12 граней в форме пятиугольников (рис.4.5).

Производные простые формы:

из кубического тетраэдра образуются следующие производные:

6) тригон-тритетраэдр – состоит из 12 граней в форме равнобедренных треугольников, образуется путём расщепления каждой грани тетраэдра на 3 треугольные грани следующим образом (рис.4.6);

7) тетрагон-тритетраэдр – 12 граней в форме четырёхугольников, образуется посредством утроения каждой грани тетраэдра следующим образом (рис.4.7);

8) пентагон-тритетраэдр – 12 граней в форме пятиугольников (рис. 4.8);

9) гексатетраэдр – 24 грани в форме треугольников, образуется посредством ушестерения каждой грани тетраэдра (рис.4.9).

Все производные от тетраэдра в первом приближении похожи на тетраэдр.

Из октаэдра аналогичным способом образуются следующие производные:

10) тригон-триоктаэдр – 24 грани в форме равнобедренных треугольников (рис.4.10);

11) тетрагон-триоктаэдр – 24 грани в форме четырёхугольников (рис.4.11);

12) пентагон-триоктаэдр – 24 грани в форме пятиугольников (рис.4.12);

13) гексоктаэдр – 48 граней в форме разносторонних треугольников (самая большая простая форма по количеству граней) (рис.4.13);

Из гексаэдра образуется одна производная форма:

14) тетрагексаэдр – 24 грани в форме равнобедренных треугольников, образуется посредством учетверения каждой грани гексаэдра (рис.4.14).

Из пентагон-додекэдра образуется одна производная:

15) дидодекаэдр – 24 грани в форме четырёхугольников, образуется посредством удвоения каждой грани пентагон-додекаэдра (рис.4.15).

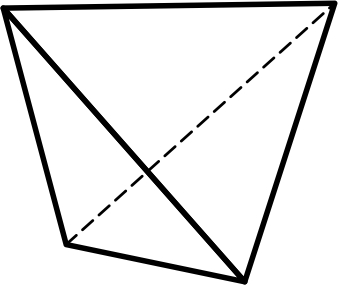
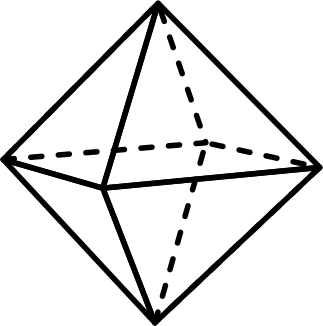
4.1 4.2 4.3

Тетраэдр Октаэдр Гексаэдр (куб)

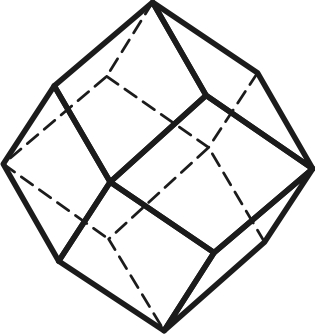
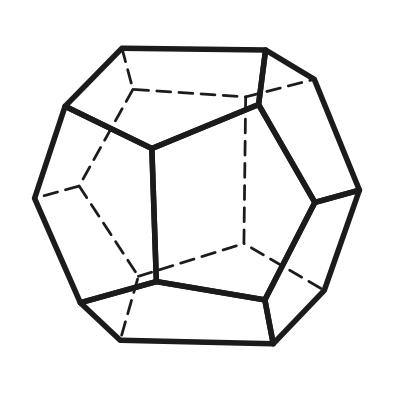
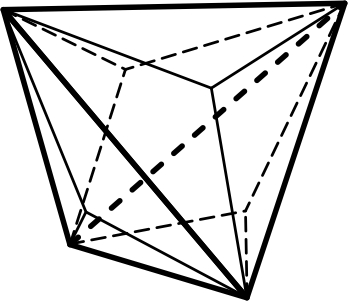
4. 4.5 4.6

Ромбо-додекаэдр Пентагон-додекаэдр Тригон-тритетраэдр

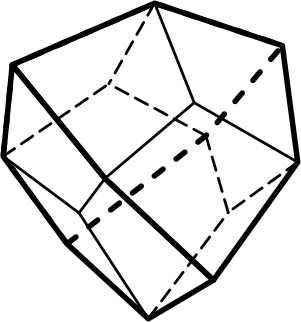
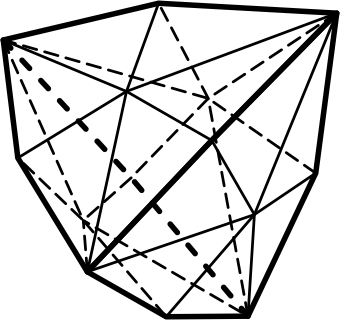
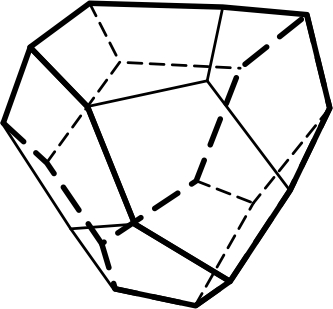
4.7 4.8 4.9

Тетрагон-тритетраэдр Гексатетраэдр Пентагон-тритетраэдр

Рис. 4. Простые формы кубической сингонии

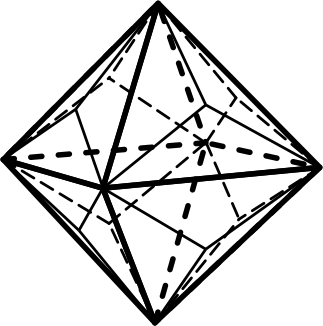
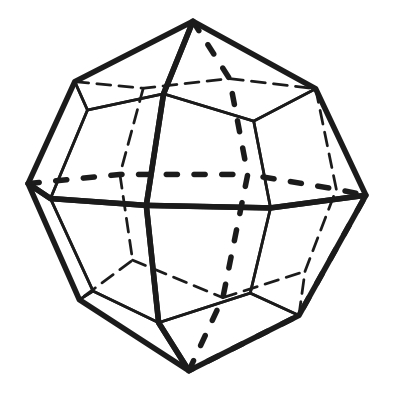
4.10 4.11 4.12

Тригон-триоктаэдр Тетрагон-триоктаэдр Гексоктаэдр

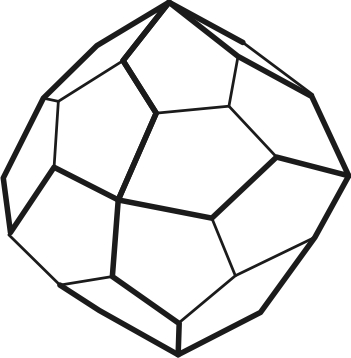
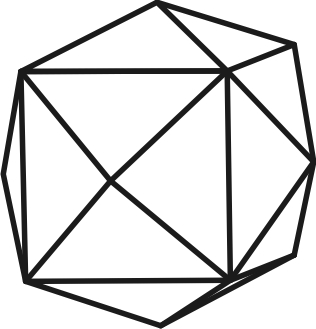
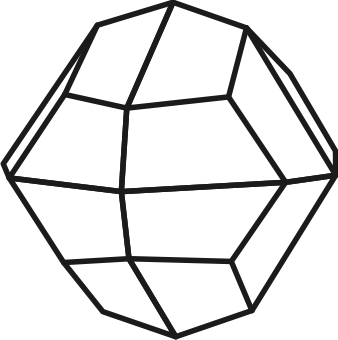
4.13 4.14 4.15

Пентагон-триоктаэдр Тетрагексаэдр Дидодекаэдр

Рис. 4. Простые формы высшей категории сингонии (окончание)

Принцип наименования простых форм кубической сингонии заключается в следующем. В сложных названиях первое слово означает форму грани (тригон – треугольник, тетрагон – четырёхугольник, пентагон – пятиугольник)\. Второе слово – количество граней в простой форме.

При указании количества граней используют следующие греческие числительные:

ди – 2; три – 3; тетра – 4; гекса – 6; окта – 8; додека – 12,

при этом 12-гранники называются по разному: додекаэдр и тритетраэдр (три – 3, тетра – 4, 3Х4 = 12). Различие в том, что тритетраэдр является производной формой и корень этого слова даёт указание, из какой основной формы она образована (из тетраэдра). Поэтому 24-гранники называются также неодинаково: триоктаэдр, гексатетрадр, дидодекаэдр, тетрагексаэдр.

Все 15 простых форм кубической сингонии являются закрытыми.