В. Ромбическая сингония

Формулы и виды симметрии:

1) 3L₂3PC – планаксиальный вид симметрии;

2) L₂2P – планальный вид симметрии;

3) 3L₂ – аксиальный вид симметрии.

Простые формы (рис. 2.1 – 2.7):

1) моноэдр (рис. 2.1);

2) пинакоид (рис. 2.2);

3) диэдр (рис. 2.3);

4) ромбическая призма (рис. 2.4);

5) ромбическая пирамида – четыре равные грани, пересекающиеся в одной точке (в поперечном сечении – ромб) (рис. 2.6);

6) ромбический тетраэдр – четыре равные грани, из которых каждые три пересекаются в одной точке (поперечное сечение через центр – ромб) (рис. 2.5);

7) ромбическая дипирамида – 8 равных граней, состоит как бы из двух равных пирамид (поперечное сечение – ромб) (рис.2.7).

Габитусы:

моноэдрический, пинакоидальный, диэдрический, ромбо-призматический, ромбо-пирамидальный, ромбо-дипирамидальный, ромбо-тетраэдрический и смешанный.

2.1 2.2 2.3

Моноэдр Пинакоид Диэдр;

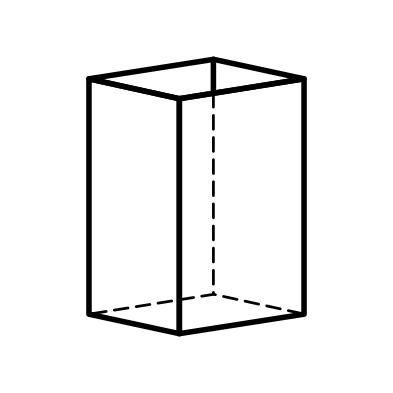
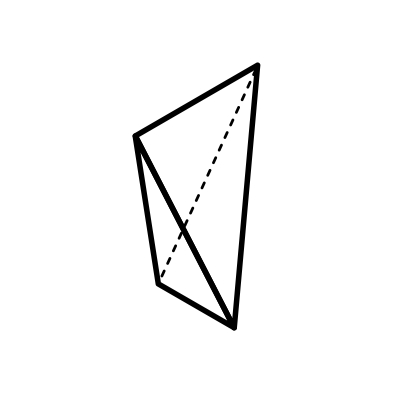
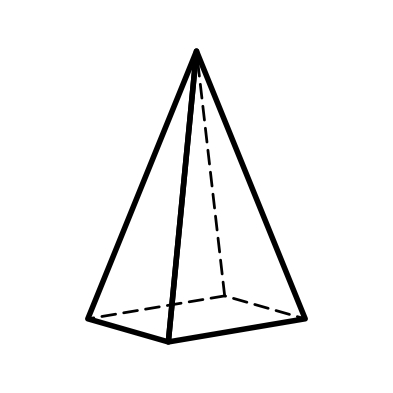
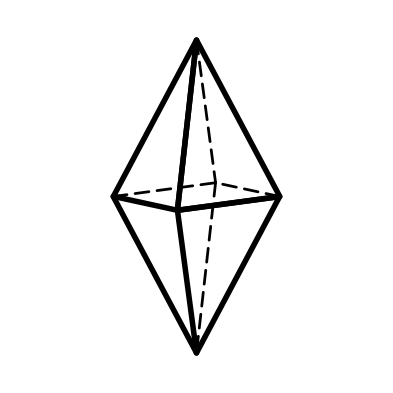
2.4 2.5 2.6 2.7

Ромбическая Ромбический Ромбическая Ромбическая

призма тетраэдр пирамида дипирамида

Рис.2. Простые формы низшей категории сингоний

1.8. Средняя категория сингоний а. Тетрагональная сингония

Формулы и виды симметрии:

1) L₄4L₂5PC – планаксиальный вид симметрии;

2) L₄4L₂ – аксиальный;

3) L₄4P – планальный;

4) L₄PC – центральный;

5) L₄ – примитивный;

6) L_i42L₂2P – инверсионно-планальный;

7) L_i4 – инверсионно-примитивный.

При нахождении в кристаллах L_i4 рекомендуется руководствоваться дополнительным признаком: ось L_i4 проявляет себя как обычная ось L₂, но она перпендикулярна квадратному сечению кристалла.

Простые формы (рис. 3.1-3.27):

1) моноэдр (рис.3.1);

2) пинакоид (рис.3.2);

3)тетрагональная призма – 4 грани, параллельные одному направлению (поперечное сечение – квадрат) (рис. 3.3);

4) дитетрагональная призма – 8 граней, параллельных одному направлению (поперечное сечение – дитетрагон) (рис.3.6);

5) тетрагональная пирамида – 4 грани, пересекающиеся в одной точке (поперечное сечение – квадрат) (рис.3.9);

6) дитетрагональная пирамида – 8 граней, пересекающихся в одной точке (поперечное сечение – дитетрагон) (рис.3.12);

7) тетрагональная дипирамида – 8 граней, состоит как бы из двух равных тетрагональных пирамид (поперечное сечение – дитетрагон) (рис.3.15);

8) дитетрагональная дипирамида – 16 граней, состоит как бы из двух равных дитетрагональных пирамид (поперечное сечение – дитетрагон) (рис.3.18);

9) тетрагональный трапецоэдр (трапеца – четырёхугольник с двумя равными соседними сторонами) – имеет 8 граней; напоминает дипирамиду, одна половина которой сдвинута относительно другой на некоторый угол, присутствует только в аксиальном виде симметрии(L₄ 4L₄) (рис.3.21);

10) тетрагональный тетраэдр – отличается от ромбического тем, что имеет поперечное сечение через центр в форме квадрата, перпендикулярно этому сечению проходит ось Li₄ (рис.3.25);

11) тетрагональный скаленоэдр (скаленос – косоугольный треугольник) – имеет 8 граней, представляет собой как бы удвоенный тетраэдр (поперечное сечение – дитетрагон, перпендикулярно ему проходит ось Li₄) (рис.3.26).

Б.Тригональная сингония

Формулы и виды симметрии:

1) L₃ 3L₂ 3PC – планальный вид симметрии;

2) L₃ 3L₂ – аксиальный;

3) L₃ 3P – планальный;

4) L₃C – центральный;

5) L₃ – примитивный.

В.Гексагональная сингония

Формулы и виды симметрии:

1) L₆ 6L₂ 7PC – планальный вид симметрии;

2) L₆ 6L₂ – аксиальный;

3) L₆ 6P – планальный;

4) L ₆PC – центральный;

5) L₆ – примитивный;

6) Li₆ (L₃P) – инверсионно-примитивный;

7) Li₆3L₂3P (L₆3L₂4P) – инверсионно-планальный.

Тригональная и гексагональная сингонии имеют общие простые формы и поэтому рассматриваются далее совместно.

Простые формы (рис.3.1-3.27):

1) моноэдр (рис.3.1);

2) пинакоид (рис.3.2);

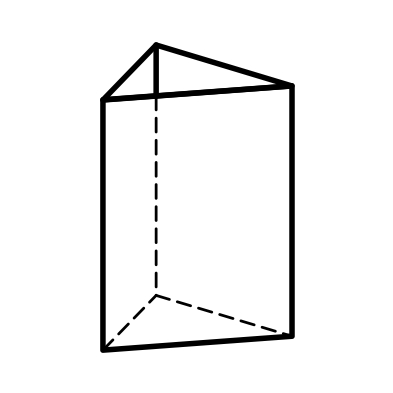
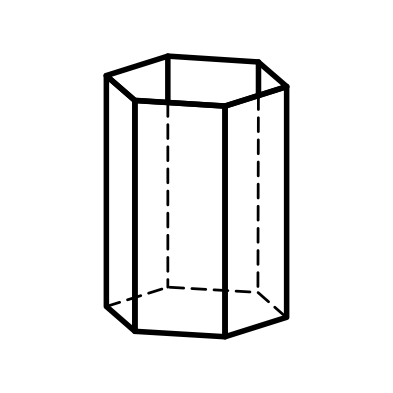
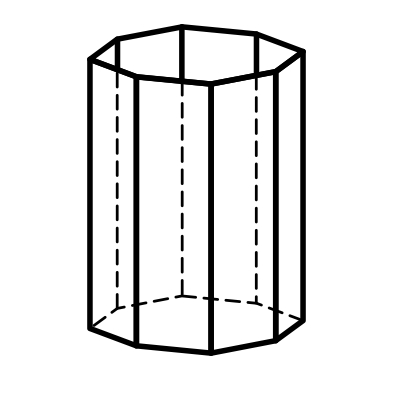
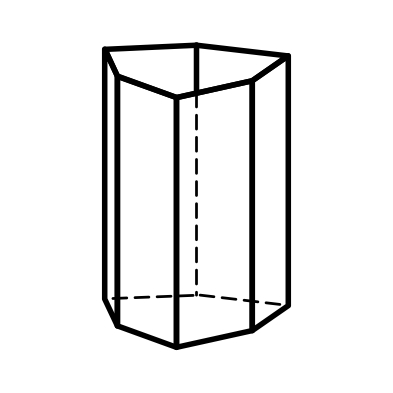
3-6) призмы: тригональные, дитригональные, гексагональные, дигексагональные (формы поперечного сечения – тригон, дитригон, гексагон, дигексагон) (рис.3.4, 3.5, 3.7, 3.8);

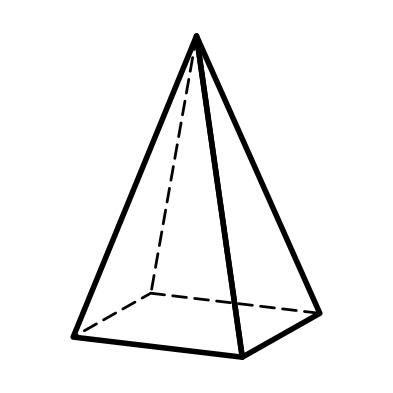
7-10) пирамиды: тригональные, дитригональные, гексагональные, дигексагональные (формы поперечного сечения – тригон, дитригон, гексагон, дигексагон) (рис.3.10, 3.11, 3.14, 3.15);

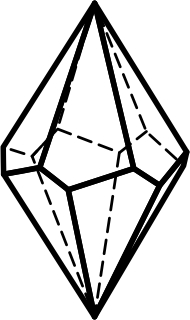
11-14) дипирамиды: тригональные, дитригональные, гексагональные, дигексагональные (формы поперечного сечения – тригон, дитригон, гексагон, дигексагон) (рис.3.13, 3.14, 3.19, 3.20);

15) ромбоэдр – имеет 6 граней в форме ромбов, каждая верхняя грань расположена симметрично относительно двух нижних и наоборот (рис.3.24);

16) дитригональный скаленоэдр – имеет 12 граней, представляет собой как бы удвоенный ромбоэдр, пара двух верхних граней располагается симметрично относительно двух пар нижних граней (рис.3.27);

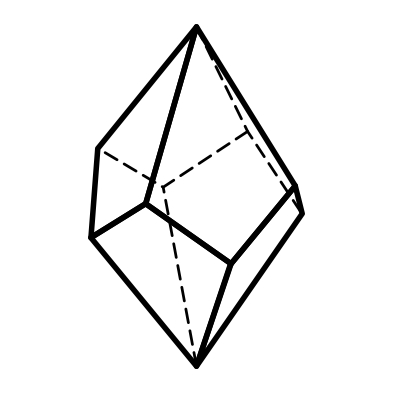
17-18) трапецоэдры: тригональный и гексагональный, имеют соответственно 6 и 12 граней, аналогично тетрагональному трапецоэдру, верхняя грань в трапецоэдре сдвинута относительно нижней на некоторый угол (рис.3.22, 3.23).

3.1 3.2 3.3

Моноэдр Пинакоид Тетрагональная призма

3.4 3.5 3.6

Тригональная призма Гексагональная призма Дитетрагональная призма

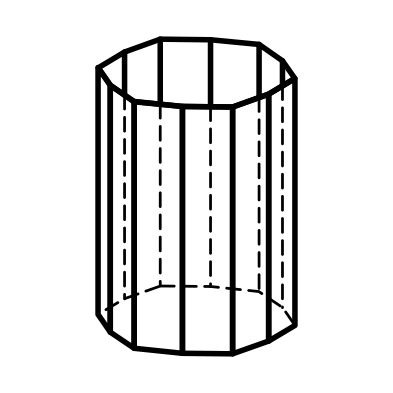
3.7 3.8 3.9

Дитригональная Дигексагональная Тетрагональная

призма призма пирамида

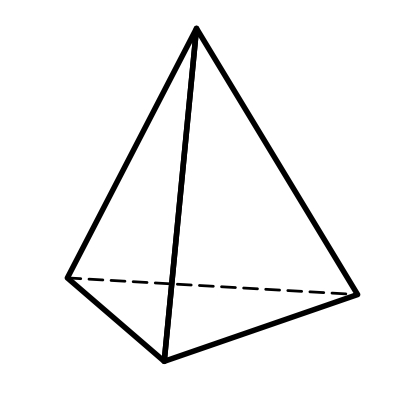
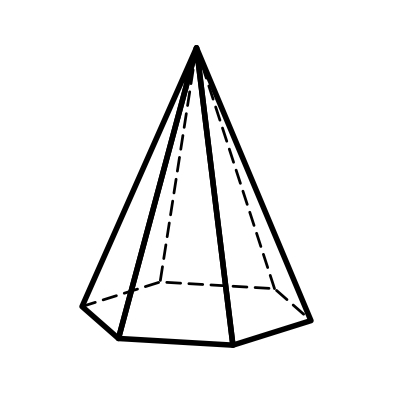
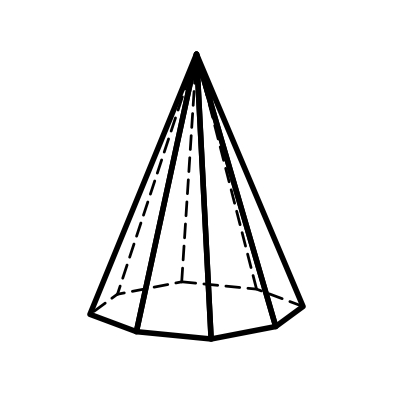
3.10 3.11 3.12

Тригональная Гексагональная Дитетрагональная

пирамида пирамида пирамида

Рис. 3. Простые формы средней категории сингоний

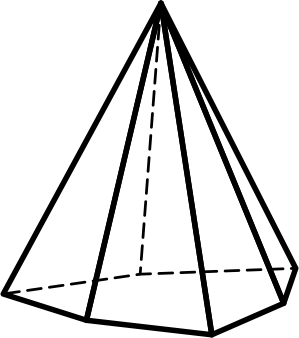
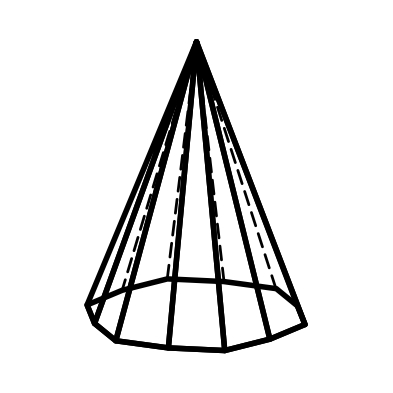
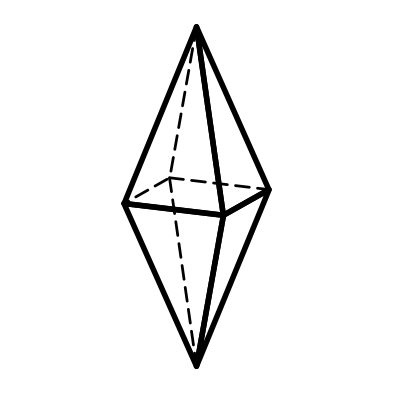
3.13 3.14 3.15

Дитригональная Дигексагональная Тетрагональная

пирамида пирамида дипирамида

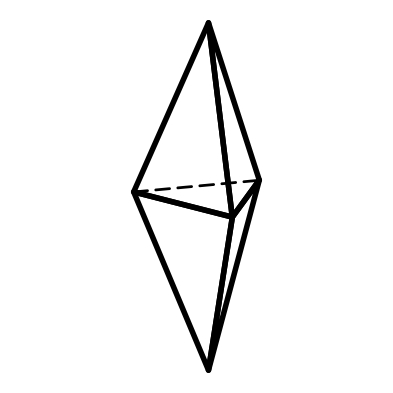
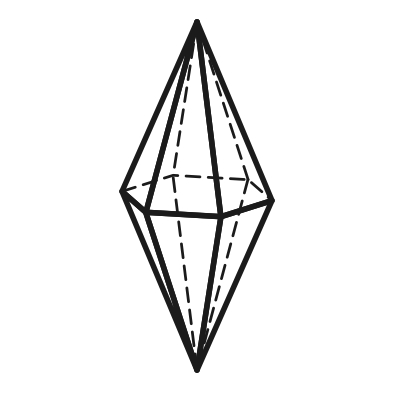
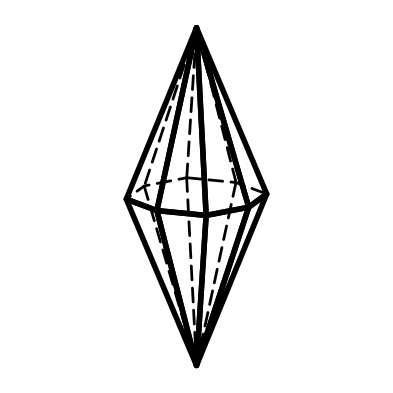
3.16 3.17 3.18

Тригональная Гексагональная Дитетрагональная

дипирамида дипирамида дипирамида

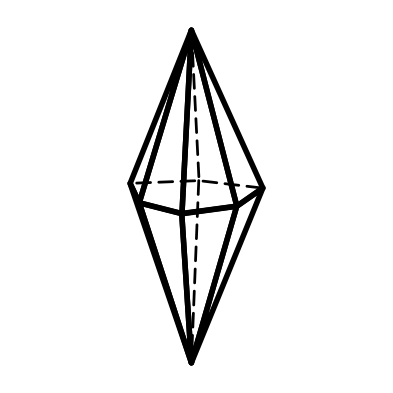
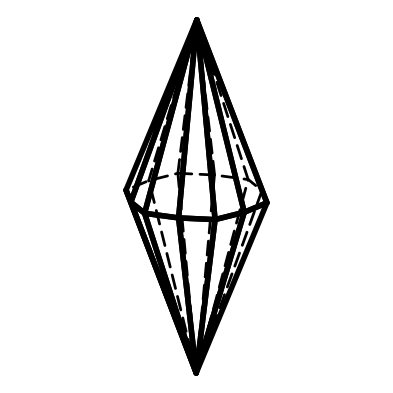
3.19 3.20 3.21

Дитригональная Дигексагональная Тетрагональный

дипирамида дипирамида трапецоэдр

Рис. 3. Простые формы средней категории сингоний (продолжение)

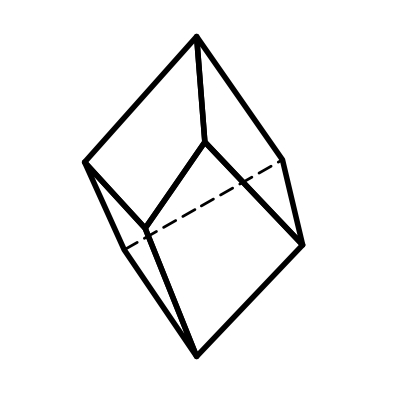
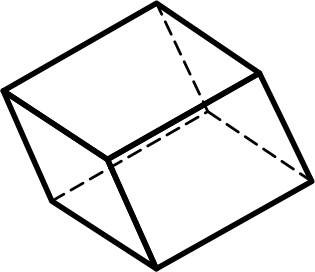
3.22 3.23 3.24

Тригональный Гексагональный Ромбоэдр

трапецоэдр трапецоэдр

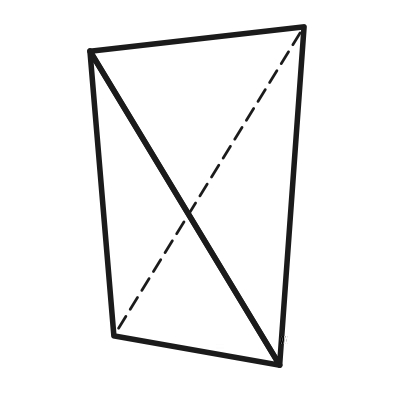
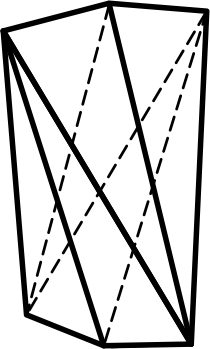
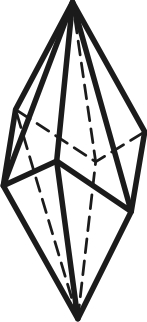
3.25 3.26 3.27

Тетрагональный Тетрагональный Дитригональный

тетраэдр скаленоэдр скаленоэдр

Рис. 3. Простые формы средней категории сингоний (окончание)