Лекция 5. Основные теоремы линейного программирования

Содержание лекционного занятия:

• Теорема об оптимальном решении в ограниченной области.

• Теорема об оптимальном решении в неограничен­ной области.

• Фундаментальная теорема.

• Теорема об альтернативном оптимуме.

• Геометрическая интерпретация симплекс-метода

Прежде чем перейти к рассмотрению основных теорем линейного программирования, вспомним понятия, рассматриваемые в курсе линейной алгебры.

Базисным (опорным) решением системы m линейных уравнений с п переменными называется решение, в кото­ром все (n-m) не основных переменных равны нулю.

Число базисных решений является конечным, так как оно равно числу групп основных переменных, не превосходящему C^m _n.

Базисное решение, в котором хотя бы одна из основных переменных равна нулю, называется вырожденным.

Теорема. Если задача линейного программирования имеет оптимальное решение, то линейная функция принимает максимальное значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся вы­пуклой линейной комбинацией этих точек.

Теорема. (Об оптимальном решении в ограниченной области.) Если область допустимых решений системы ограничена, то оптимальное решение существует и совпадает хотя бы с одним из опорных решений системы.

Теорема. (Об оптимальном решении в неограничен­ной области.) Если область допустимых решений не огра­ничена, то оптимальное решение, совпадающее, по крайней мере, с одним из опорных решений, существует только тог­да, когда линейная функция ограничена сверху для задачи максимизации или снизу для задачи минимизации.

Теорема. (Фундаментальная.) Если задача линейного программирования имеет оптимальное решение (в ограни­ченной области всегда, а в неограниченной области в зави­симости от ограниченности линейной функции), то оно совпадает, по крайней мере, с одним из опорных решений системы ограничительных уравнений.

Теорема. (Об альтернативном оптимуме.) Если мак­симум или минимум линейной функции достигается в не­скольких опорных решениях, то любое оптимальное решение есть выпуклая линейная комбинация оптимальных решений.

Геометрическая интерпретация симплекс-метода

Из приведенных выше основных теорем линейного пре­мирования следует, что если задача линейного пре­мирования имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает, по крайней мере, с одним из допустимых базисных решений системы ограничений.

На основании этого можно предложить достаточно простой метод решения задачи линейного программирования, который сводится к следующей принципиальной схеме:

• необходимо найти все опорные решения (точки много­гранника), множество которых является конечным;

• вычислить для каждого из опорных решений значение целевой функции;

• сравнить значения целевой функции в каждом из опорных решений и выбрать оптимальное (максималь­ное или минимальное).

Теоретически данная схема приведет к нахождению оптимального решения, но практически ее осуществление связано с большими вычислительными трудностями.

Если же указанный перебор опорных решений произво­дить направленно, т.е. на каждом из шагов улучшая (или, по крайней мере, не ухудшая) значение целевой функции, то число перебираемых опорных решений можно резко сокра­тить, что в конечном итоге приводит к весьма существенно­му сокращению числа шагов при отыскании оптимума целе­вой функции. При использовании такой схемы, в отличие от первой, каждое последующее опорное решение выбирается таким образом, чтобы оно было лучше, (или, по крайней ме­ре, не хуже) предыдущего, именно поэтому на каждом из шагов значение целевой функции улучшается (или, по край­ней мере, не ухудшается).

Фундаментом универсального метода решения задач иного программирования, который называется симплекс-методом, является метод направленного перебора. (По латыни симплекс означает — простой, что в данном случае интерпретируется как простой выпуклый многогранник.)

Геометрическая интерпретация симплекс-метода состоит в последовательном переходе от одной вершины многогран­ника к другой (от первоначально выбранной вершины к од­ной из соседних вершин, а именно к той, у которой линейная функция принимает лучшее или, по крайней мере, не худшее значение). Этот процесс происходит до тех пор, пока не бу­дет найдено оптимальное решение — вершина, где достига­ется оптимальное значение функции (если задача имеет ко­нечный оптимум).

Идея симплекс-метода разработана русским ученым Л.В. Канторовичем в 1939 г. На основе этой идеи американ­ский ученый Д. Данциг в 1949 г. разработал симплекс-метод, позволяющий решить любую задачу линейного программи­рования.

В настоящее время на основе этого метода разработан пакет программ, с применением которого решаются задачи линейного программирования.

Вопросы для самоконтроля:

1.Основные элементы линейной алгебры. Их роль при построении модели.

2.Анализ моделей на чувствительность. Виды моделей.

Рекомендуемая литература:

1.Ашманов С.А. Линейное программирование. —М.: Наука, 1981.

2.Айсагалиев А.С., Айсагалиева С.С. Лекции по методам оптмизации.-Алматы:Гылым,1996

Лекция 6. Двойственные задачи линейного программирования

Содержание лекционного занятия:

• Прямая задача

• Двойственная задача

Одним из центральных и наиболее значительных мест в теории линейного программирования является двойственность, которая состоит в том, что каждой исходной (прямой) задаче, в которой целевая функция стремится к максимуму (минимуму):

F = c₁,x₁,+с₂х₂+с₃х₃+... + с_nх_n ->max(min), (1)

система функциональных ограничений представляет собой систему неравенств:

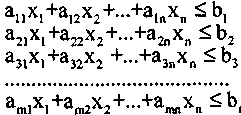( 2)

система прямых ограничений также представляет собой систему неравенств:

(3)

соответствует двойственная задача, в которой:

• целевая функция стремится к минимуму (максимуму):

Z(y) = y₁,b₁, +y₂b₂+...+ y_mb_m -»min(max) (4)

• система функциональных ограничений, представляет собой систему неравенств:

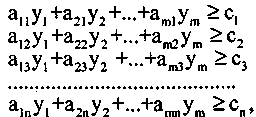
(5)

• система прямых ограничений также представляет со­бой систему неравенств:

у₁0,_У20,_Уз0..._Уm0. (6)

Общим для прямой и двойственной задач является то, что в каждой из них отыскивается экстремум линейной функции, а искомые переменные должны удовлетворять системам функциональных и прямых ограничений. Кроме того, в обеих задачах используются одни и те же парамет­ры: элементы матрицы А, вектор В, вектор С.

Отличие между прямой и двойственной задачей состоит в том, что в прямой задаче определяются значения n пере­менных x₁,x₂,...,x_n, а в двойственной — m переменных: y_1, y_2,…, y_m в исходной задаче ищется максимум, а в двой­ственной — минимум целевой функции, знаки неравенств в этих задачах противоположны, компоненты вектора огра­ничений в одной из задач являются коэффициентами при переменных в целевой функции другой задачи.

Чтобы к заданной прямой задаче сформировать двойст­венную, целесообразно пользоваться определенной систе­мой формальных правил.

1. Число переменных в двойственной задаче равно коли­честву функциональных ограничений в прямой задаче (т.е., если в прямой задаче вектор переменных записывается, как n-мерный вектор-столбец, то в двойственной задаче вектор переменных будет представлять собой m-мерный вектор — строку и наоборот).

2. Если прямая задача ставится как задача максимизации, то двойственная — как задача минимизации и наоборот.

3. Компоненты вектора функциональных ограничений В=(bi,b2,...b_m) в прямой задаче становятся коэффициентами целевой функции в двойственной задаче.

Применение этих трех правил позволяет сформировать целевую функцию двойственной задачи:

Z(y) = y₁ b₁ + у₂b₂ +...+ y_rab_m -> min .

4. 

   Матрица коэффициентов при переменных в системе функциональных ограничений двойственной задачи получается транспонированием матрицы коэффициентов при переменных в системе функциональных ограничений прямой задачи.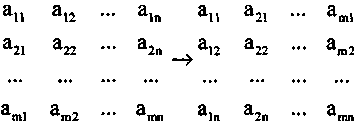

5. Знак неравенств функциональных ограничений в прямой задаче меняется на обратный в двойственной, т.е. « » на « ».

6. Коэффициенты целевой функции прямой задачи c₁,c₂,...,c_n, становятся вектором ограничений в двойственной задаче.

Применяя правила 4, 6 мы можем сформировать систему функциональных ограничений обратной задачи:

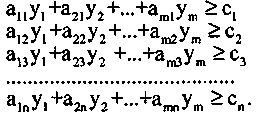
7. Прямые ограничения на неотрицательность перемен­ных для двойственной задачи сохраняются.

_У10,у₂0,у₃0...у_m0

Таким образом, исходную и двойственную к ней задачу можно представить следующим образом:

Прямая и двойственная задача, построенная в соответствии с рассмотренными выше правилами, называются сим­метричными взаимодвойственными задачами.

Если к двойственной задаче снова построить двойствен­ную задачу, то получим прямую (т.е. исходную) задачу. Необходимо отметить, что ни одна из двойственных задач не является основной, так как если поставлена одна из за­дач, то другая может быть сформулирована как двойствен­ная и каждая из них является двойственной по отношению к другой.

Вопросы для самоконтроля:

1.Понятие о двойственных задачах ЛП.

2.Теорема двойственности.

Рекомендуемая литература:

1.Измаилов А.Ф., Солодов М.В. Численные методы оптимизации. М.: Физматлит, 2003.

2.Банди Б. Методы оптимизации. Вводный курс. М.: Радио и связь, 1988.

Лекция 7. Содержательная интерпретация прямой и двойст­венной задачи

Содержание лекционного занятия:

• Прямая задача

• Двойственная задача

• Основное неравенство теории двойственности

Прямая задача. Для изготовления n видов продукции предприятие ис­пользует m видов ресурсов, которые имеются на предприя­тии в количестве: b₁, b₂,..., b_m. При этом количество каждо­го из ресурсов i (i=l...m), которое идет на производство единицы продукции j-го вида (j=l...n), задается технологи­ческими коэффициентами а_ij. Выручка, получаемая пред­приятием от продажи единицы изготовленной продукции j-го вида (j=l...n), составляет соответственно c₁,c₂,...c_n. Не­обходимо составить такой план производства продукции X=(x₁,x₂,...x_n), при котором выручка предприятия от реали­зации всей продукции, изготовленной в соответствии с данным планом, будет максимальной, а количество каждо­го из ресурсов, используемых для выполнения заданного плана, не превысит имеющегося на предприятии запаса каждого из них.

Таким образом, в данной задаче:

• целевая функция: F = c₁x₁, + c₂x₂ + c₃x₃ +... + c_n x_n —» max отражает цель предприятия, которая заключается в макси­мизации выручки от продажи продукции, изготовленной в соответствии с оптимальным планом X=(x₁,x₂,...x_n);

• каждое из неравенств, входящих в систему функцио­нальных ограничений:

отражает требования, предъявляемые к данному плану, ко­торые состоят в том, что количество каждого из видов ре­сурсов i (i=l...m), необходимых для производства каждого j-ro вида продукции (j=l...n) в количестве x_j, не должно превышать запасов b_j каждого из ресурсов, имеющихся на предприятии;

• каждое из неравенств, входящих в систему прямых ог­раничений: х10,х20,...,хn0 отражает требования, состоящие в том, что количество каж­дого j-ro вида продукции (j=l...n) не может быть отрица­тельным.

Двойственная задача. Предположим, что то же предприятие, которое для про­изводства n видов продукции использует m видов ресурсов, при тех же самых технологических коэффициентах a_ij хочет минимизировать затраты на используемые ресурсы. Для этого ему необходимо найти такие оценки (цены) каждого из ресурсов — у_i (i=l.. .m), при которых затраты на них бы­ли бы минимальны, при этом искомые оценки (цены) ресурсов должны быть установлены таким образом, что за­траты на производство единицы продукции каждого j-ro вида не превышали бы выручки от ее реализации.

В данном случае под оценками (ценами) подразумева­ются объективно обусловленные оценки (понятие, впервые введенное Л. Канторовичем), которые, в отличие от цен, задаются не извне, а определяются самим предприятием для внутреннего пользования.

Таким образом, в данной задаче:

• целевая функция: Z(y) = y₁ b₁, + у₂b₂ +... + y_mb_m -> min отражает цель предприятия, которая заключается в мини­мизации затрат;

• каждое из неравенств, входящих в систему функцио­нальных ограничений:

отражает требования, предъявляемые к искомым оценкам — y1, y2, …, ym которые выражаются в том, что затраты на производство единицы каждого j-го (j=l...n) вида продук­ции не превышают выручки от ее реализации (т.е. ее цены);

• каждое из неравенств, входящих в систему прямых ог­раничений: У10,у20,...,уm0

отражает требования, предъявляемые к оценкам, которые заключаются в том, чтобы каждая из них — уi (i = l...m) должна быть неотрицательной.