Лекция 3. Различные формы задач линейного программирования

Содержание лекционного занятия:

• Стандартная форма задачи линейного программирования

• Каноническая форма задачи линейного программи­рования (ЗЛП)

• Переход от стандартной формы задачам линейного программирования (ЗЛП) к канонической

Рассмотренные выше примеры задач линейного про­граммирования укладываются в общий класс задач линей­ного программирования. Однако записи целевых функций и главным образом ограничений в них существенно разли­чаются. В первом примере искомые переменные зависят от одного индекса и ограничения имеют вид неравенств; в другом примере искомые переменные зависят от двух ин­дексов, а ограничения имеют вид равенств. Существует также ряд практических задач, в которых часть ограниче­ний представлена в виде равенств, а часть — в виде нера­венств.

Различают три основные формы задачи линейного про­граммирования, к которым может быть сведена любая со­держательная постановка задачи.

Общая форма задачи линейного программирования

Задана система m линейных уравнений с n переменны­ми:

(1)

x_j >0, где(j = l...n) , (2)

а линейная функция:

F = c₁ x₁ +с₂ x₂+с₃ x₃+... + c_n x_n → max(min). (3)

Необходимо найти такой вектор Х=(х₁, х₂,х₃ , x_n), который удовлетворяет ограничениям (1) и (2) и при котором линейная функции F принимает максимальное (или минимальное) значение.

Как видно из представленной выше записи, в общей форме задачи линейного программирования система огра­ничений (1) включает в себя как равенства, так и нера­венства, а целевая функция может стремиться как к макси­муму, так и к минимуму.

Более кратко задачу линейного программирования в общей форме можно представить в следующем виде:

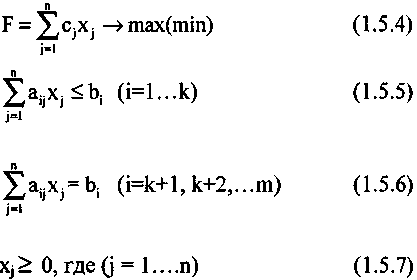
Оптимальным решением (или оптимальным планом) за­дачи линейного программирования называется решение Х*=(х*₁ ,х*₂...х_n), удовлетворяющее системам ограничений, при которой линейная функция F достига­ет оптимального значение (минимума или максимума).

Термины «решение» или «план» — синонимы, одна­ко первый используется чаще, когда речь идет о формали­зованной постановке задачи, а второй — о содержательной.

Стандартная форма задачи линейного программирования

Задача линейного программирования, представленная в форме:

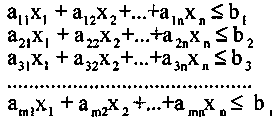
а линейная функция:

F = c₁ x₁ +с₂ x₂+c₃ x₃+... + c_т x_т->max(min),

называется стандартной формой задачи линейного программирования.

Особенность данной формы состоит в том, что в ней система как функциональных, так и прямых ограничений состоит из одних неравенств, переменные xj ≥0, где (j=l...n) являются неотрицательными, а целевая функция может стремиться как к минимуму, так и к максимуму.

Каноническая форма задачи линейного программи­рования (злп)

Форма, в которой:

F= c₁ x₁ +c₂ x₂+c₃ x₃+... + c_n x_n->max

все переменные Xj — неотрицательны, система ограниче­ний представляет собой систему уравнений, а целевая функция стремится к максимуму, называется канонической формой задачи линейного программирования.