Градиентные методы

Градиентным методом называется метод, по которому на каждом шаге очередная точка определяется по формуле

(1)

т.е. направление спуска на каждой итерации - это анти­градиент, вычисленный в текущей точке х^к.

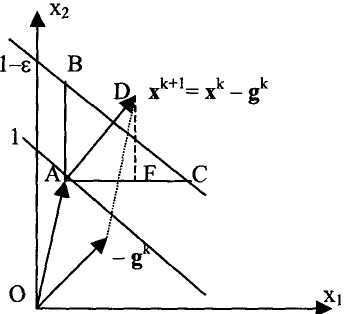
Рис. 4. Линии уровня и антиградиент

На рис. 4 текущему вектору х^к соответствует точка А. Примем за единицу значение целевой функции в этой точке и рассмотрим линию уровня со значением 1-ε, где ε доста­точно малая величина. При достаточно малом е эти линии уровня будем считать параллельными. Переход на линию уровня с меньшим значением при изменении только x₁ дает точку С, а при изменении только х₂ точку В. Обозначим расстояние АС через Δ₁ ,а АВ через Δ₂. Тогда для частных производных имеем приближенные равенства: дF/дх₁ = - ε /Δ₁ и дF/дх₂ = -ε/ Δ₂.

Градиентный метод, в котором на каждой итерации ис­пользуется шаг до точки минимума в направлении антиградиента, называется методом наискорейшего спуска.

Название наискорейший спуск не должно вводить в за­блуждение, так как оно вовсе не означает, что метод позво­ляет найти минимум за наименьшее число шагов по сравне­нию с другими методами.

Траектория спуска в этом методе носит зигзагообразный характер и градиенты в любых двух последовательных точ­ках ортогональны (рис. 6).

Рис. 6. Зигзагообразная траектория наискорейшего спуска

Метод параллельных касательных

Алгоритм состоит в следующем:

1. Из точки х⁰ делаем два шага как в методе наискорейшего спуска (рис. 6) и получаем точку х².

2. Из точки х² идем не по антиградиенту, а по направлению х²-х⁰(рис. 7).

3. Находим х³ как точку минимума функции в этом направ­лении и вычисляем антиградиент в ней.

4. Проверяем условия окончания счета и, если они не вы­полнены, повторяем пункт 1, используя х³ вместо х⁰.

В методе наискорейшего спуска информация об уже пройденных точках не хранилась и никак не использова­лась. А в методе параллельных касательных надо запоми­нать пройденные точки, так как они используются для вы­бора направления спуска. Эта идея использования инфор­мации, полученной в процессе поиска минимума, для ускорения сходимости лежит в основе многих методов оптимизации.

Метод сопряженных градиентов

Идея этого метода в том, чтобы на каждом шаге в каче­стве направления спуска использовать не антиградиент, а его линейную комбинацию с прежним направлением спус­ка. Если обозначить через р^к направление спуска на k-ой итерации, то последовательность векторов р^к строится сле­дующим образом:

1. р⁰ = -g⁰, т.е. первый шаг делаем по антиградиенту,

2. p^k+1 = -g^k+1 + β_kp^k, где β_к = (g^k+', g^k+') / (g^k, g^k).

Это означает, что

Другими словами, сделав из начальной точки один шаг по методу наискорейшего спуска, надо вычислить антиградиент в новой точке. Затем взять отноше­ние квадратов длин нового и старого градиентов (это и есть β₀), умножить старый антиградиент на это число и результат сложить с новым антиградиентом. Это и будет направление спуска р¹= -g¹ – β₀ g⁰, которое мы будем использовать вместо антиградиента -g¹. В направлении р¹ нужно дойти до точки минимума, в ней вычислить анти­градиент –g² затем β₁= (g², g²) / (g¹ ,g¹) и р² = -g² + β₁ p¹ и т.д.