Задача выпуклого программирования

Рассмотрим задачу нелинейного программирования

(4)

при ограничениях

, (5)

. (6)

Для решения сформулированной задачи в такой общей постановке не существует универсальных методов. Однако для отдельных классов задач, в которых сделаны дополнительные ограничения относительно свойств функ­ций f(x) и , разработаны эффективные методы их решения.

Говорят, что множество допустимых решений задачи (4) - (6) удов­летворяет условию регулярности, или условию Слейтера, если существует, по крайней мере, одна точка , принадлежащая области допустимых ре­шений такая, что . Задача (4) - (6) называется задачей выпуклого программирования, если функция является во­гнутой (выпуклой), а функции - выпуклыми. Функцией Лагранжа задачи выпуклого программирования (4) - (6) называется функция

,

где - множители Лагранжа.

Точка называется седловой точкой функции Лагранжа, если для всех и .

Теорема 1 (Куна - Таккера): Для задачи выпуклого програм­мирования (4) - (6), множество допустимых решений которой обладает свойством регулярности, является опти­мальным решением тогда и только тогда, когда существует такой вектор , что - седловая точка функции Лагранжа.

Если предположить, что функции f и непрерывно дифференци­руемы, то теорема Куна - Таккера может быть дополнена аналитическими выражениями, определяющими необходимые и достаточные условия того, чтобы точка была седловой точкой функции Лагранжа, т. е. являлась решением задачи выпуклого программирования:

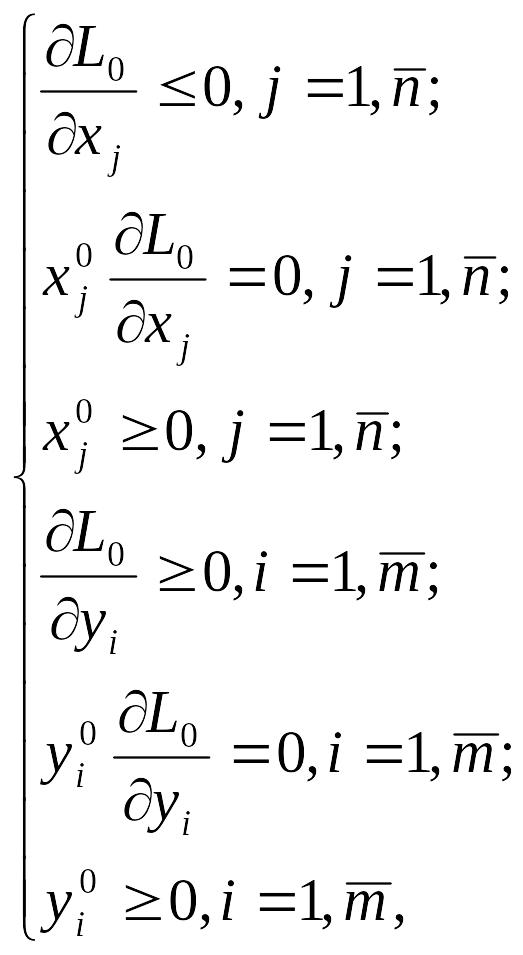
где и значения соответствующих частных производных функции Лагранжа, вычисленных в седловой точке.

Вопросы для самоконтроля:

1.Понятия и сущность о выпуклом программировании.

2.Теорема Куна - Таккера.

3.Метод множителей Лагранжа.

Рекомендуемая литература:

1.Ашманов С.А. Линейное программирование. —М.: Наука, 1981.

2.Айсагалиев А.С., Айсагалиева С.С. Лекции по методам оптмизации.-Алматы:Гылым,1996

Лекция 11 . Методы безусловной оптимизации

Содержание лекционного занятия:

• Градиентные методы

• Метод параллельных касательных

• Метод сопряженных градиентов

• Метод покоординатного спуска

• О методах второго порядка

• О методах прямого поиска

• Методы одномерной минимизации

Это методы поиска минимума функции многих пере­менных при отсутствии ограничений.

Итерационные методы минимизации функции F(x) со­стоят в построении последовательности векторов, т.е. точек х⁰, х¹,..., х^kтаких что F(x0) > F(x¹) > ... > F(x^k) > ... Любой такой метод называется методом спуска. Естественно, должна быть обеспечена сходимость получаемой последо­вательности точек к точке минимума, т.е. рассматриваются методы, позволяющие получить точку минимума за конеч­ное число шагов или приблизиться к ней достаточно близко при соответствующем числе шагов. К сожалению, здесь нельзя употребить слова «сколь угодно близко при неогра­ниченном увеличении числа шагов». Дело в том, что тео­ретически все сходящиеся методы этим свойством облада­ют, но практически близость к минимуму в задачах боль­шой размерности ограничивается ошибками вычислений, которые обусловлены погрешностью представления чисел в компьютере. Поэтому необходимо вести вычисления с удвоенной точностью, выбирая соответствующие типы дан­ных при разработке конкретных компьютерных программ.

Для построения итерационной последовательности необхо­димо выбрать начальное приближение х⁰. В задачах с ограниче­ниями это должна быть допустимая точка, а в задачах без огра­ничений— теоретически любая точка. Однако целесообразно использовать всю имеющуюся информацию о поведении целе­вой функции F(x), чтобы выбрать х⁰ поближе к точке минимума.

После того как начальное приближение получено, прежде чем перейти к следующей точке, нужно принять два решения:

1. Выбрать направление, по которому пойдем из х⁰ в точку с меньшим значением целевой функции (направление спуска);

2. Определить величину шага по направлению спуска. При любом методе спуска итерационная последователь­ность точек{х^к} может быть записана в виде: х^к+'=х^к + λ_кp_к,(к = 0, 1,...),

где вектор р^к — это направление, а λ_к||р^к|| — величина шага. Если ||р^к|| =1, т.е. длина вектора спуска равна единице, то величина шага равна λ_к. Отметим, что иногда λ_к называ­ют шагом независимо от длины вектора р^к. Здесь — длина вектора р^к.

Методы спуска отличаются процедурами построения вектора р^к и вычисления λ_к. При этом могут использоваться одна (последняя) или две последние (или более) из уже по­лученных точек.

Для задач безусловной минимизации любое направление является возможным (никакие ограничения не мешают), но далеко не все направления приемлемы. Нас могут интересо­вать только направления, обеспечивающие убывание целе­вой функции, хотя бы при достаточно малом шаге. Предпо­лагая непрерывность первых частных производных целевой функции и используя ее разложение в ряд Тэйлора в произ­вольной точке х, получим F(x + λр) ≈ F(x) + λ(g, p). Здесь g— градиент функции, вычисленный в точке х. Отсюда следует, что приращение функции F(x + λр) - F(x) < 0 при отрицательном скалярном произведении (g, p). Итак, направление спуска должно составлять острый угол с ан­тиградиентом. Этот вывод справедлив и для задач с огра­ничениями, но там еще дополнительно требуется, чтобы при достаточно малом шаге не нарушалось ни одно из огра­ничений.

Все такие направления называются подходящими (приемлемыми). Методы спуска, позволяющие получать последовательно подходящие направления, Зойтендейк (Zoutendijk G.) назвал методами возможных направлений.