Метод множителей Лагранжа

Рассмотрим частный случай общей задачи нелинейного программиро­вания, предполагая, что система ограничений содержит только уравнения, отсутствуют условия неотрицательности переменных, и - функции, непрерывные вместе со своими частными производными. Ограничения в задаче заданы уравнениями, поэто­му для ее решения можно воспользоваться классическим методом отыскания условного экстремума функций нескольких переменных. Вводят набор переменных , называемых множителями Лагранжа, и составляют функцию Лагранжа

,

находят частные производные

и рассматривают систему n+m уравнений

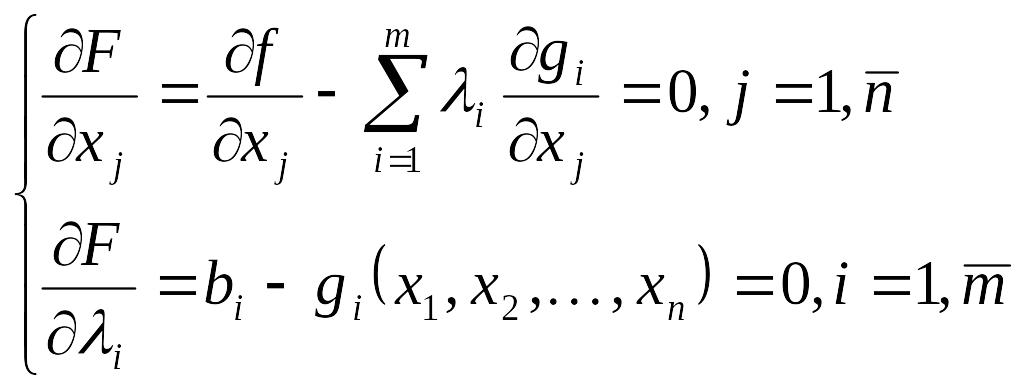(1)

с n+m неизвестными , . Решив систему уравне­ний (1), получают все точки, в которых функция может иметь экстре­мальные значения. Дальнейшее исследование найденных точек проводят так же, как и в случае безусловного экстремума. Метод множителей Лагранжа имеет ограниченное применение, так как система (1), как правило, имеет несколько решений.

Выпуклое программирование

Определение: Функция , заданная на выпуклом множестве X, называется выпуклой, если для любых двух точек и из X и любо­го выполняется соотношение

. (2)

Определение: Функция , заданная на выпуклом множестве X, называется вогнутой, если для любых двух точек и из X и любо­го выполняется соотношение

(3)

Если неравенства (2) и (3) считать строгими и они выполняются при , то функция является строго выпуклой (строго вогнутой). Выпуклость и вогнутость функций определяется только относительно выпуклых множеств.

Если , где , - выпуклые (вогнутые) функции на некотором выпуклом множестве , то функция f(x) - также выпуклая (вогнутая) на X.

Основные свойства выпуклых и вогнутых функций:

1. Множество точек минимума выпуклой функции, заданной на выпук­лом множестве, - выпукло.

2. Пусть f(x) - выпуклая функция, заданная на замкнутом выпуклом множестве . Тогда локальный минимум f(x) на X является и глобальным.

3. Если глобальный минимум достигается в двух различных точках, то он достигается и в любой точке отрезка, соединяющего данные точки.

4. Если - строго выпуклая функция, то ее глобальный минимум на выпуклом множестве X достигается в единственной точке.

5. Пусть функция f(x) - выпуклая функция, заданная на выпуклом множестве X, и, кроме того, она непрерывна вместе со своими частными производными первого порядка во всех внутренних точках X. Пусть - точка, в которой . Тогда в точке достигается локальный минимум, совпадающий с глобальным минимумом.

6. Множество точек глобальных (следовательно, и локальных) мини­мумов выпуклой функции , заданной на ограниченном замкнутом вы­пуклом множестве X, включает хотя бы одну крайнюю точку; если множест­во локальных минимумов включает в себя хотя бы одну внутреннюю точку множества X, то является функцией-константой.