Указания к лабораторным работам по

НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ (СТРОИТЕЛЬСТВО)

Тени в ортогональных проекциях.

Понятие о собственной и падающей тени (рис. 1).

Рис. 1 Собственная и падающая тень

Тень на неосвещенной части поверхности предмета называется собственной. Тень, отбрасываемая на плоскости и поверхности, называется падающей. Линия, отделяющая освещенную часть предмета от неосвещенной называется контуром собственной тени. Контур падающей тени является тенью от контура собственной тени.

Источники света.

Освещение предмета называется факельным (рис. 2, а), если источник света удалён от объекта на незначительном расстояние. Когда источник света удален в бесконечность и световые лучи параллельны друг другу, освещение называется солнечным (рис. 2, б).

а) б)

Рис. 2 Освещение

Чаще всего построение теней осуществляется при параллельных световых лучах.

Стандартное направление световых лучей.

В ортогональных проекциях направление лучей принято брать по диагонали куба (рис. 3).

а) б)

Рис. 3 Стандартное направление световых лучей

Такое направление лучей света удобно при построении теней, оно соответствует примерно полуденному стоянию солнца на широтах Москвы и Санкт-Петербурга летом, когда тени в натуре получаются более резкими.

Тень точки.

Тенью точки является след светового луча, проходящего через данную точку (рис. 4).

Рис. 4 Тень точки

А_1t – тень точки на плоскости π₁.

А_2t – тень точки на плоскости π₂.

Если y_А > z_А, то реальная тень на плоскости π₁.

Если z_А > y_А, то реальная тень на плоскости π₂.

Тень точки на той плоскости проекции, которую световой луч пересекает первой называется реальной, а тень точки на плоскости, которую световой луч пересекает второй называется мнимой. Мнимую тень, если она необходима при построении, обозначают круглыми скобками.

Тень от прямой общего положения (рис. 5).

Рис. 5 Тень от прямой общего положения

Если тень от прямой падает на две пересекающиеся плоскости, то на линии их пересечения тень имеет излом.

Тени от прямых частного положения (рис. 6).

Тень от прямой, перпендикулярной плоскости проекции, совпадает с проекцией светового луча на той плоскости проекции, которой прямая перпендикулярна.

Тень от прямой, параллельной плоскости проекций, параллельна проекции прямой и равна ей по величине на той плоскости проекции, которой прямая параллельна.

Рис. 6 Тени от прямых частного положения

Тени от плоских фигур.

Тень от треугольника.

На рис. 7 построена падающая тень от плоскости общего положения, заданной треугольником ABC на плоскости проекций. Тени от вершин треугольника оказались на разных плоскостях проекций. Построение тени треугольника следует вести в той же последовательности, как и построение тени прямой. Сначала строят тень на плоскости π₁, включая и часть мнимой тени, а затем строят тень на плоскости π₂. Тень треугольника преломится и перейдет с плоскости π₁ на плоскость π₂. Затем определяется освещенность треугольника методом конкурирующих точек. Берется фронтальная проекция любой точки K на треугольнике, затем определяется ее горизонтальная проекция. Проводят лучи света через точку K. При определении видимости на фронтальной плоскости проекций берут конкурирующие точки на луче света и стороне треугольника AB, а на горизонтальной плоскости – на луче света и стороне AC. В результате определения видимости понятно, что обе проекции будут освещенными.

Рис. 7 Тени от треугольника

Тень от круга.

На рис. 8 представлено построение тени от круга. Сначала строится тень от центра круга (реальная и мнимая). Для построения тени на горизонтальной плоскости проекций из мнимой тени от центра круга проводим дугу окружности радиусом круга. Для определения тени от круга на фронтальной плоскости проекций строим тени от точек 1, 5, 6, 7, 8 (она получится в виде части эллипса). Соединяем все полученные тени точек и точки пересечения дуги окружности с осью x и получаем тень от круга.

Рис. 8 Тени от круга

Тени в нишах (рис. 9).

Ниша – это углубление в стене. Тень, падающая от фронтального обрамления ниши, повторит его форму на задней грани. Построим тень в прямоугольной нише. Для этого достаточно найти тень от точки 1 и через точку 1_2t провести контур тени, повторяющий форму обрамления.

а)

б)

Рис. 9 Тени в нишах

Тени поверхностей.

При построении теней поверхностей сначала следует определить контур собственной тени, а затем приступить к построению падающей тени, которая является тенью контура собственной тени.

Тень от призмы (рис. 10).

Задняя и правая боковая грани призмы находятся в собственной тени. Ребра, разделяющие освещенные и затененные грани призмы, образуют контур собственной тени. Они представляют собой прямые частного положения, падающие тени от которых строятся просто.

Рис. 10 Тени от призмы

Тень от пирамиды (рис. 11).

Если тень пирамиды падает одновременно на две плоскости проекций π₁ и π₂, то она будет иметь излом. В этом случае необходимо вначале построить тень от вершины S, найдя реальную S_2t и мнимую (S_1t) тени, а затем зная точки 1_t и 2_t, которые получим проведя прямые S_1tВ₁ и S_1tD₁, определим контур падающей тени и решим вопрос об освещенности отдельных граней пирамиды.

Рис. 11 Тень от пирамиды

Тень от цилиндра (рис. 12).

Кон­тур собственной тени цилиндра определяется двумя образующими, проходящими через точки 1 и 5, по которым лучи света касаются его боковой поверхности. Затем строятся падающие тени от точек 1, 2, 3, 4, 5 и соединяются.

Рис. 12 Тень от цилиндра

Тень от конуса (рис. 13).

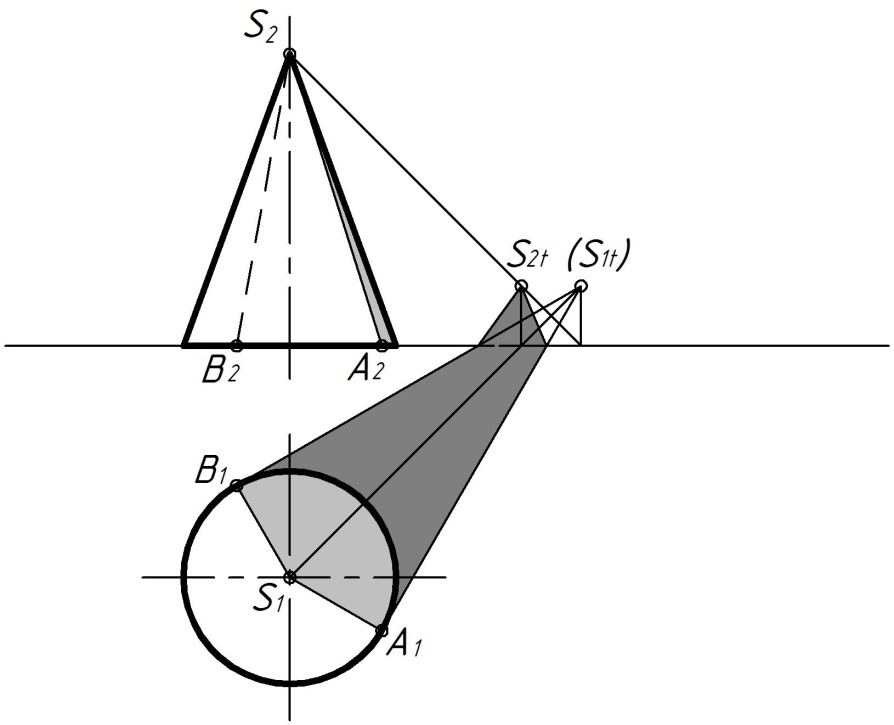
Рис. 13 Тень от конуса

Построим собственные и падающие тени конуса. Для этого необходимо провести к поверхности конуса касательные плоскости, параллельные лучам света, и определить линии касания. Вдоль этих линий, являющихся образующими конуса, пройдет контур собственной тени конуса. Практически построение выполняется так. Вначале определяют реальную тень S_2t падающую от вершины конуса на плоскость π₂ и мнимую (S_1t), падающую плоскость π₁. Затем из (S_1t) проводят прямые, касательные к основанию конуса, и определяют точки касания А и В. Через точки касания А и В проводят образующие конуса SА и SВ, которые вместе с дугой основания образуют контур собственной тени конуса. Касательные S_1tА и S_1tВ к основанию конуса являются линиями контура падающей тени конуса. Падающая тень конуса имеет точки излома на оси x.

Методы построения теней.

а) Метод лучевых секущих плоскостей.

б) Метод обратного луча.

Метод лучевых секущих плоскостей.

Сущность метода состоит в том, что для построения тени, падающей от одного объекта на другой, через характерные точки объекта проводится ряд лучевых секущих плоскостей, строятся по точкам вспомогательные сечения и определяются точки пересечения ряда лучевых прямых, проведенных через характерные точки первого объекта, с построенными сечениями второго. Построив ряд точек падающей тени и соединив их в определенной последовательности, получим контур падающей тени (рис. 14).

Рис. 14 Метод лучевых секущих плоскостей

Метод обратного луча.

Сущность этого метода заключается в следующем (рис. 15, 16):

1) Строятся падающие тени двух предметов.

2) Определяются точки пересечения падающих теней.

3) Обратным лучом находят тень точек пересечения на исходном чертеже.

4) Найденные точки соединяются.

Рис. 15 Тень от прямой на треугольник

Рассмотрим построение тени от прямой на конус (рис. 16). Световые лучи, проходящие через прямую, образуют лучевую плоскость, которая пересекает конус по кривой второго порядка и представляет собой падающую тень от прямой на конусе. Сначала строим собственные и падающие тени конуса и падающие тени прямой на плоскость π₁. Затем отмечаем точку 1_1t пересечения контуров теней и с помощью обратного луча определяем точку тени 1₁ на теневой образующей конуса. В ней кривая падающей тени касается луча. Для построения промежуточных точек падающей тени проводим вспомогательную образующую и строим падающую тень образующей на плоскости π₁. Отмечаем точку тени 2_1t пересечения контуров теней и обратным лучом определяем точку тени на конусе. Затем аналогично находим точку тени 3 и др. Фронтальные проекции этих точек строим с помощью образующих конуса. Затем эти точки соединяем с учетом видимости.

Рис. 16 Тень от прямой на конус

Перспектива.

Основные элементы перспективы. Перспектива точки.

Перспективой называется наглядное изображение предмета, построенное методом центрального проецирования.

Различают три вида перспектив:

1) Линейная.

2) Панорамная.

3) Купольная.

Наглядное изображение, построенное на плоскости методом центрального проецирования, называется линейной перспективой.

Наглядное изображение, построенное на внутренней поверхности цилиндра, называется панорамной перспективой.

Наглядное изображение, построенное на внутренней поверхности сферы или эллипсоида, называется купольной перспективой.

Перспектива точки (рис. 17).

Рис. 17 Перспектива точки

K – вертикальная плоскость проекции (картинная плоскость или картина).

K₁ – основание картины.

π₁ – предметная плоскость.

h – линия горизонта.

S – точка зрения.

S₁ – основание точки зрения.

SP – главное расстояние картины.

P – главная точка картины.

P₁ – основание главной точки картины.

А' – перспектива точки А.

А'₁ – вторичная проекция точки А.

Если точка находится в бесконечности, то ее вторичная проекция всегда лежит на линии горизонта. Если точка принадлежит картинной плоскости, то перспектива точки совпадает с самой точкой, а вторичная проекция точки всегда лежит на основании картины. Если точка принадлежит предметной плоскости, то перспектива точки и ее вторичная проекция совпадают.

Перспектива прямых общего положения (рис. 18).

Изображение в перспективе прямой линии, расположенной в пространстве, будет также в виде прямой, как результат пересечения двух плоскостей: картины и лучевой плоскости, которая образована совокупностью лучей зрения, проецирующих отдельные точки заданной прямой. Так как положение прямой в пространстве определяется двумя её точками, то и перспектива прямой определяется перспективами двух её точек. На рис. 18 перспектива прямой AB и её вторичная проекция определены перспективами и вторичными проекциями двух её точек A и B, заданных в ортогональных проекциях. Точками, определяющими перспективу прямой, являются: начальная точка прямой (N) и бесконечно удаленная (предельная) точка прямой (F).

Рис. 18 Перспектива прямой

Перспектива прямых частного положения.

а) Горизонтальные прямые, точки схода которых в перспективе располагаются на линии горизонта (рис. 19).

Рис. 19 Перспектива горизонтальной прямой

б) Прямые, перпендикулярные картине, точкой схода которых является главная точка картины P (рис. 20).

Рис. 20 Перспектива прямой, перпендикулярной картине

в) Горизонтальные прямые, расположенные по углом 45° к картине, точками схода которых в перспективе являются дистанционные точки D₁ и D₂ (рис. 21).

Рис. 21 Перспектива прямой, расположенной под углом 45° к картине

г) Прямые, параллельные картине, не имеют точек схода, их перспективы параллельны самим прямым (рис. 22).

Рис. 22 Перспектива прямой, параллельной картине

Перспектива параллельных прямых.

Перспективы параллельных прямых пересекаются, т. е. имеют одну точку схода (рис. 23).

Рассмотрим построение перспективы параллельных прямых. Продолжив каждую из прямых до пересечения с картиной, найдем их начальные точки N. Второй точкой, определяющей искомые перспективы, будет общая, бесконечно удаленная точка F, для построения которой из точки зрения S проведем луч параллельно данным прямым.

Рис. 23 Перспектива параллельных прямых

Выбор картинной плоскости и точки зрения.

При выборе точки зрения рекомендуется придерживаться следующих положений (рис. 24):

1) Линия горизонта выбирается в зависимости от вида перспективы:

а) H ≈ 1,7 м. Перспектива с нормальной точкой зрения (для одного здания).

б) H ≈ 100 м. Перспектива с высоким горизонтом (для группы зданий).

в) H ≈ 0 м. Перспектива снизу (для отдельных деталей, наблюдаемых снизу, и для зданий, стоящих на возвышении).

Рис. 24

2) Картинная плоскость проводится через один из углов здания. Угол наклона картинной плоскости к фасаду – 25° – 35°.

3) Положение точки зрения должно обеспечивать хорошую обозреваемость предмета. Его составные части не должны загораживать друг друга.

4) Угол зрения (угол между проецирующими лучами, направленными в крайние точки плана предмета) φ = 18° – 53°. Оптимальный угол зрения – 28°. Наибольший размер (0_к0'_к) картины примерно вдвое меньше расстояния от точки зрения до картинной плоскости (S₁P₁), т. е. S₁P₁/0_к0'_к ≈ 2.

5) Главный луч зрения должен быть направлен перпендикулярно картинной плоскости и делить картину примерно пополам или находиться в средней трети между крайними лучами, идущими от зрителя к предмету.

Способы построения перспективы.

1) Радиальный способ (способ следа луча, способ Дюрера).

2) Способ архитекторов:

а) С одной точкой схода.

б) С двумя точками схода.

3) Способ прямоугольных координат.

4) способ перспективной сетки.

Радиальный способ.

Сущность радиального способа построения перспективы заключается в определении точек пересечения проецирующих лучей с картинной плоскостью, с помощью построения картинных следов прямых. Он находит применение при построении фронтальных перспектив улиц, внутренних дворов, фасадов зданий с выступающими вперед частями и т. д.

Положительной стороной метода является простота теории, позволяющая без знания теоретических основ линейной перспективы осуществлять перспективное проецирование. Отрицательной стороной является загроможденность изображения линиями вспомогательных построений, наложение перспективного изображения на ортогональный чертеж и др.

Перспектива точки, построенная радиальным методом (рис. 25).

Рис. 25 Перспектива точки А, построенная радиальным способом

Способ архитектора с двумя точками схода.

Основан на использовании двух точек схода перспектив параллельных горизонтальных прямых объекта (рис. 26).

Рис. 26 Перспектива плоской фигуры, построенная способом архитектора с двумя точками схода

Способ архитектора с одной точкой схода.

Основан на использовании одной точки схода и картинных следов прямых (рис. 27).

Рис. 27 Перспектива плоской фигуры, построенная способом архитектора с одной точкой схода

Перспектива здания с использование одной точки схода и опущенного плана (рис. 28).

Рис. 28 Перспектива здания

Деление отрезков прямой на равные и пропорциональные соотношения.

Отрезки, параллельные плоскости картины, можно делить в заданном отношении непосредственно в перспективе. Отрезки, не параллельные картине, можно разделить в заданном отношении (делительный масштаб) при помощи вспомогательных отрезков, параллельных плоскости.

Задача. Разделить отрезок АВ на 4 равных части, а отрезок СD увеличить в два раза (рис. 29).

а)

б)

Рис. 29 Деление и увеличение отрезков

Перспектива окружности.

Для построения перспективы окружности строится квадрат, описывающий окружность. Его стороны параллельны и перпендикулярны картине (рис. 30).

Диагональ квадрата является прямой, наклоненной к линии горизонта под углом в 45°. В перспективе ее точкой схода будет левая дистанционная точка D.

Рис. 30 Перспектива окружности

Способы построения перспективы.

Способ прямоугольных координат имеет ограниченное применение (рис. 31). Он используется главным образом при изображении несложных объектов неправильной формы. Сущность этого способа заключается в построении перспективы объекта, отнесенного к прямоугольной системе координат с помощью изображения в перспективе координатной системы.

Координатные оси, построенные в перспективе, называют перспективным масштабом. Ось x – называют масштабом широт, ось z – масштабом высот, ось y – масштабом глубин. По осям x и z откладывают натуральные единицы измерения. По оси y их откладывают с помощью дистанционной точки D.

Способ перспективной сетки (рис. 32). Этот способ является разновидностью координатного способа. Применяют при построении «планировочных» перспектив с высоким горизонтом при проектировании градостроительных и промышленных объектов, расположенных на значительной территории.

После выбора точки зрения на исходный план объекта наносят сетку фронтально расположенных квадратов со стороной, равной 1, 2, 5, 10, … м. По сторонам сетки ставят буквенные и цифровые обозначения ячеек. На фасаде отмечают размыры высот объектов.

Рис. 31 Способ прямоугольных координат

Рис. 32 Способ перспективной сетки

Тени в перспективе.

Тень точки.

Если источник света находится за спиной наблюдателя, то его перспектива – ниже линии горизонта (рис. 33, а).

Если источник света перед лицом наблюдателя, то его перспектива выше линии горизонта (рис. 33, б).

Если источник света солнечный, то вторичная проекция светового луча берется на основании картины, а световые лучи идут направо под углом 45° (рис. 33, в).

а) б) в)

Рис. 33 Тень от точки

Тени от прямых.

Тень от прямой сходится в ту же точку на линии горизонта, куда сходится перспектива этой точки (рис. 34).

а)

б)

Рис. 34 Тени в перспективе

Проекции с числовыми отметками.

Проекции с числовыми отметками применяются при проектировании сооружений, у которых высота несравненно мала с длиной и шириной. Применяется при проектировании автомобильных и железных дорог, аэродромов, гидросистем и оборонительных сооружений.

Проекция точки.

Сущность проекций с числовыми отметками состоит в том, что горизонтальная плоскость проекций принимается за условный нулевой уровень π₀, от которого и производится отсчет. Вторая плоскость проекций заменяется цифрой, которая указывает положение точки по высоте к плоскости π₀. Если числовая отметка имеет положительный знак, то точка находится над плоскостью, если отрицательный, то под плоскостью π₀. Все числовые отметки на чертежах указываются в метрах (рис. 35).

а) б)

Рис. 35 Точки в проекциях с числовыми отметками