Вычисление статистических параметров невзвешенного ряда способом условной средней

Кроме непосредственного (обычного) способа вычисления средней арифметической и сигмы существует способ условной средней, который может быть использован в тех случаях, когда значения признака выражены целыми числами, а появляющиеся в процессе вычисления дроби затрудняют ход решения.

Например, известны даты зацветания ольхи кустарниковой за 14 лет в днях от 1 марта V (1 столбец таблицы 3).

Таблица 3
Даты зацветания, в днях от 1 марта, V	Условное отклонение, Χс (V-C)	Xс2
65	-7	49
67	-5	25
69	-3	9
70	-2	4
71	-1	1
72	0	0
72	0	0
73	1	1
73	1	1
78	6	36
81	9	81
85	13	169
86	14	196
87	15	225
	∑Χс =S1=41	∑Χс =S2=807

Вероятней всего, средняя арифметическая будет выражена дробным числом. Чтобы избежать в вычислениях дробности, возьмем любое целое число, близкое к середине этого ряда, например, 72. Назовем его условной средней и обозначим “C”. В нашем примере C=72. Находим отклонения каждого значения V от C, это будут условные отклонения X_c (2 столбец таблицы 3). Сумму этих отклонений назовем первой вспомогательной величиной S₁. Она равна 41. Каждое условное отклонение возводим в квадрат. При суммировании получаем вторую вспомогательную величину S₂. Она равна 807. Ход решения напоминает непосредственный способ вычисления, когда среднее квадратическое отклонение вычисляется по формуле: .

Но у нас получена другая величина ∑Χ_с =S₂. Используя вспомогательные значения S₁ и S₂, находим M и σ:

, . Если захотим проверить правильность решения, вычислим M непосредственным способом: . Вспомним, что средняя определяется на один порядок более точно, чем даны значения признака. Чтобы найти сигму, используем формулу:

, , .

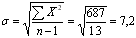Прочие параметры данного статистического ряда определим следующим образом: ошибка средней арифметической ,

достоверность средней арифметической ,

так как t>t_st, то результат достоверен; коэффициент вариации .

Для показателей разнообразия тоже можно определять ошибки репрезентативности:

для сигмы – ,

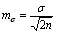для коэффициента вариации – .

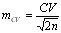В нашем примере , .

Наряду с достоверностью можно применять показатель точности опыта, то есть процент, который составляет ошибка средней арифметической

В нашем примере .

Если значения P<5%, то такая точность допустима, если P<2%, то такая точность высокая. Ошибка точности находится по формуле .

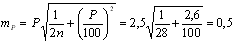Эти параметры дают довольно полное представление о данном статистическом незавершенном ряде. В среднем за 14 лет ольха кустарниковая зацветает через 74,9 дня от 1 марта, то есть округленно 14 мая, с ошибкой 1,9 дня и с доверительным интервалом на 0,95 уровне: 13,9±2*1,9; то есть самый ранний срок зацветания 10 мая и самый поздний – 18 мая. Варьирование годовых дат зацветания сравнительно невелико, так как коэффициент вариации равен: V=9,6±1,8%. Полученные параметры заслуживают доверия ввиду большой достоверности средней арифметической: t_M=38,9, 38,9»3 и значения показателя точности опыта меньше 5%: P;=(2,5%±0,5%)<5%.