1.3.7. Математическая модель звена формирования возмущений (μ → λ), где λ – возмущающее воздействие

Возмущающим воздействием для объекта регулирования (см. выше) является λ(t) – относительное возмущение (в долях номинальных значений возмущающих сигналов), которое складывается из двух возмущений: колебаний параметров притока λ₁(t) и колебаний параметров оттока λ₂(t),

.

1.4 Разработка структурной схемы системы автоматического управления

Структурная схема системы автоматического управления уровнем жидкости в резервуаре может иметь вид:

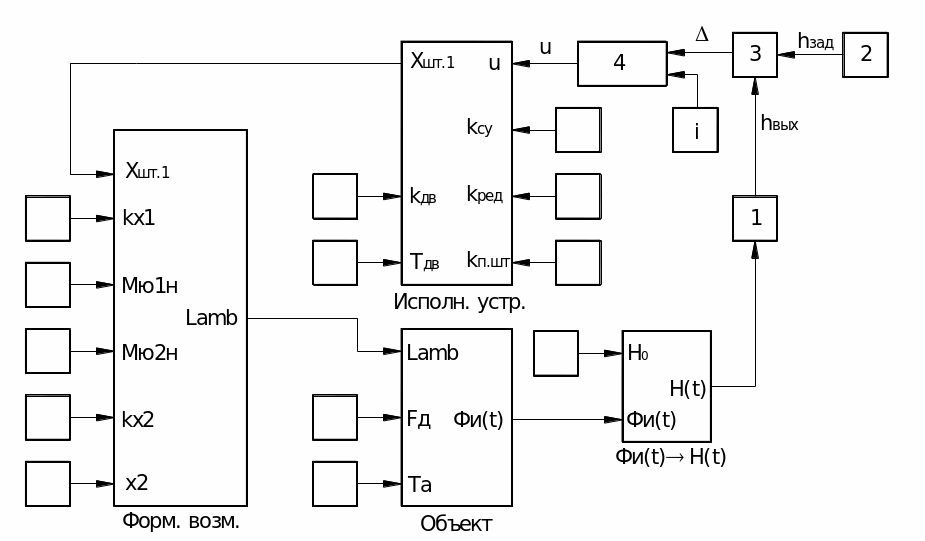
Рис. 5. Структурная схема системы автоматического регулирования уровня жидкости в резервуаре.

Форм.возм. – звено, формирующее возмущение; Объект - объект регулирования (емкость); Фи(t)→H(t) – подпрограмма, формирующая значение H(t); Исполн. устр. – исполнительное устройство.

1 – датчик уровня; 2 – задатчик уровня; 3 – элемент сравнения; 4 – регулятор.

Н₀ – высота жидкости в резервуаре при номинальных параметрах кранов; Н(t) – текущая высота жидкости в резервуаре; h_вых – сигнал датчика уровня; h_зад – сигнал задатчика уровня; ∆ – сигнал рассогласования; u - сигнал регулятора; Фи(t) – относительное значение уровня жидкости в резервуаре; Lamb – относительное возмущение; Х_шт,1, х₂ - перемещение штоков кранов на притоке и оттоке соответственно; Мю1н, Мю2н – номинальные значения коэффициентов истечения кранов на притоке и оттоке соответственно; kx₁, kx₂ – коэффициенты передачи кранов на притоке и оттоке соответственно; F_Д – коэффициент самовыравнивания; Т_а – время разгона объекта, k_ДВ – коэффициент передачи электродвигателя; Т_ДВ – постоянная времени электродвигателя; k_СУ, k_П.ШТ., k_РЕД – коэффициенты передачи согласующего устройства, привода штока вентиля и редуктора соответственно.

1.5 Инструментальная модель системы автоматического регулирования уровня жидкости в резервуаре

Реализовать модель будем в пакете MATLAB, при этом воспользуемся инструментом визуального моделирования SIMULINK.

Представим четыре модели в виде подсистем: модель объекта регулирования, модель формирователя возмущений, модель исполнительного устройства и модель регулятора.

1.5.1. Инструментальная модель объекта регулирования

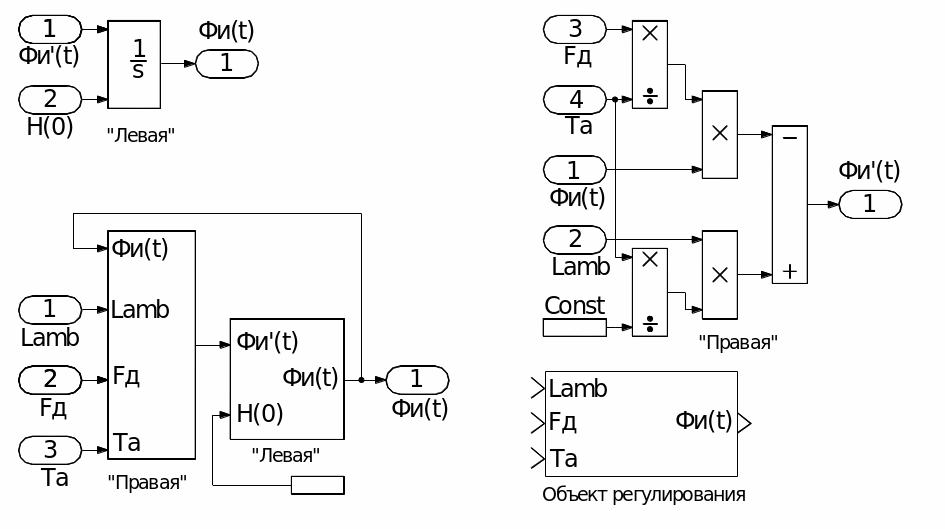
Рис.6. Инструментальная модель объекта регулирования.

1.5.2. Инструментальная модель формирователя возмущений

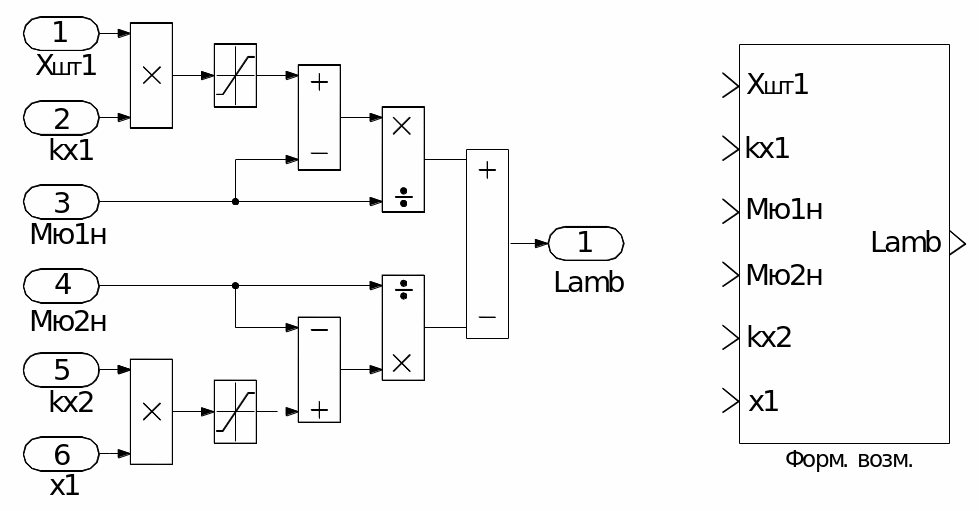
Рис. 7. Инструментальная модель звена формирующего возмущения.

1.5.3. Инструментальная модель исполнительного устройства

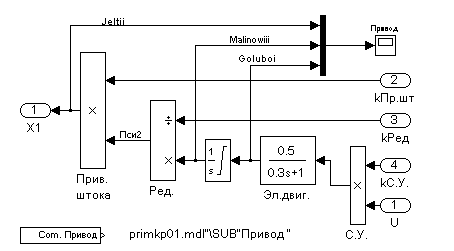
Рис. 8. Инструментальная модель исполнительного устройства.

1.5.4. Инструментальная модель регулятора

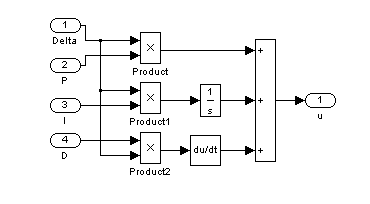
Рис. 9. Инструментальная модель регулятора.

Общая схема инструментальной модели, системы автоматического регулирования уровня жидкости в емкости, представлена на рисунке

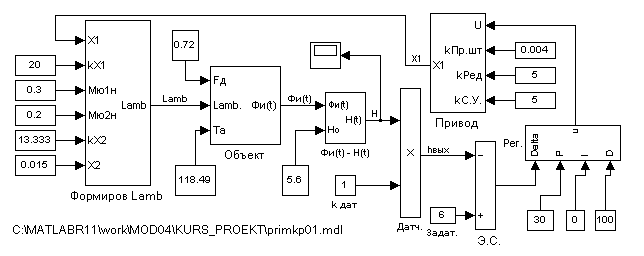
Рис. 10. Инструментальная модель системы автоматического управления.

1.6 Исследование модели ( указания по выполнению оптимизации)

Исследование модели заключается в планировании и проведении экспериментов с моделью с заданной целью.

В данной работе целью проведения экспериментов является настройка параметров регулятора наилучшим образом, по сути оптимизация. Важным вопросом здесь является постановка задачи оптимизации, который будет разъяснен далее.

Чтобы приступить к оптимизации необходимо найти начальные удовлетворительные настройки регулятора.

Удовлетворительными (или допустимыми) настройками регулятора являются настройки при которых время регулирования составляет не более 2-3Т (где Т – постоянная времени объекта регулирования), а величина перерегулирования составляет не более 30%. Нужно учитывать, чтобы перерегулирование не приводило к "нереальным" графикам (например, когда высота емкости 4.5 м, а Нmax на графике переходного процесса более 4.5).

Таким образом, начальные допустимые настройки регулятора могут быть получены «методом проб и ошибок» вручную или, что более приветствуется, например, методом Циглера-Никольса.

После того, как допустимые удовлетворительные настройки найдены необходимо, осуществить процесс оптимизации данных настроек.

Процесс оптимизации представляет собой целенаправленный перебор (поиск) параметров с целью достижения экстремума целевой функции. Целевой функцией в ТАУ может служить один из критериев качества регулирования технологических параметров, при этом остальные критерии качества могут учитываться в качестве ограничений.

Например, наиболее простой и понятной постановкой задачи оптимизации является следующая:

, при условии

Таким образом, необходимо найти настройки регулятора P, I и D при которых, время регулирования T минимально, при этом значение перерегулирования не более 30 %.

В данном примере САР, допустимыми настройками являются настройки, приведенные в таблице 1.

Оптимизация настроек регулятора проводится различными методами.

Метод оптимизации с переходом по первому улучшению:

1. Шаг: выбрать допустимые начальные параметры для оптимизации (P=20, I=0 D=100) затем установить значения шага поиска по каждому параметру равный порядка 10% от начальных значений параметров (по каждому направлению, то есть Sh_P=2, Sh_I=0.1, Sh_D=10).

2. Шаг: осуществить пробный шаг по направлению P c шагом Sh_P=2, получим две точки в трехмерном пространстве параметров поиска (то есть получим точку (P=22, I=0 D=100) и точку (P=18, I=0 D=100)). По очереди подставляем значения параметров регулятора в модель и рассчитаем для них значения показателя качества Т и ограничения . Если в одной из данных точек значения показателя Т лучше (т.е. меньше), а ограничение не нарушается (то есть не превышает 30%), то запоминаем эту точку и идем на шаг 3. Если не в одной из новых двух точек показатель качества не улучшился, то переходим на шаг 3. Например, лучшей оказалась точка (P=22, I=0 D=100), с ней и будем далее работать.

3. Шаг: осуществить пробный шаг по направлению I c шагом Sh_I=0.1, получим две точки в трехмерном пространстве параметров поиска (то есть получим точку (P=22, I=0.1 D=100) и точку (P=22, I=-0.1 D=100), вторая, заметим, не имеет физического смысла). По очереди подставляем значения параметров регулятора в модель и рассчитаем для них значения показателя качества Т и ограничения . Если в одной из данных точек значения показателя Т лучше (меньше), а ограничение не нарушается (то есть не превышает 30%), то запоминаем эту точку и ее показатель качества, затем идем на шаг 4. Если не в одной из новых двух точек показатель качества не улучшился, то переходим на шаг 4. Например, лучшей оказалась точка (P=22, I=0.1 D=100), с ней и будем далее работать.

4. Шаг: осуществить пробный шаг по направлению D c шагом Sh_D=0.1, получим две точки в трехмерном пространстве параметров поиска (то есть получим точку (P=22, I=0.1 D=110) и точку (P=22, I=0.1 D=90)). По очереди подставляем значения параметров регулятора в модель и рассчитаем для них значения показателя качества Т и ограничения . Если в одной из данных точек значения показателя Т лучше (меньше), а ограничение не нарушается (то есть не превышает 30%), то запоминаем эту точку и идем на шаг 5. Если не в одной из новых двух точек показатель качества не улучшился, то переходим на шаг 5. Например, лучшей оказалась точка (P=22, I=0.1 D=90), с ней и будем далее работать.

5. Шаг: если на одном из шагов 3, 4 или 5 была найдено улучшение параметров регулятора, то переходим на шаг 3 и продолжаем поиск, иначе идем на шаг 6.

6. Шаг: составляем окрестность последней найденной улучшенной точки в пространстве параметров и заносим данные в таблицу. (например, если для точки (P=22, I=0.1 D=90) выполнить шаги 3-5 и не будет улучшений, то таблица окрестности данной точки будет выглядеть как таблица 2.

Таблица 1 - Результаты определения допустимых параметров регулятора

P	I	D	Время регулирования	Перерегулирование	Статическая ошибка	Примечания.
18	0	60	50	0.06	≈ 0	Колебания практически отсутствуют
20	0	80	21	0.012	≈ 0	Колебания практически отсутствуют
20	0	100	21	0.012	≈ 0	Колебания практически отсутствуют
20	2	100	30	0.028	≈ 0	Колебания практически отсутствуют

Таблица 2 – Оптимальная точка и ее окрестность

P	I	D	Время регулирования	Перерегулирование	Статическая ошибка	Примечания.
22	0.1	90	50	0.06	≈ 0	Оптимальные параметры. Колебания практически отсутствуют
24	0.1	90	60	0.012	≈ 0
20	0.1	90	61	0.04	≈ 0
22	0.2	90	80	0.012	≈ 0
22	0.0	90	70	0.06	≈ 0	Колебания практически отсутствуют
22	0.1	100	55	0.012	≈ 0	Колебания практически отсутствуют
22	0.1	80	59	0.02	≈ 0	Колебания практически отсутствуют

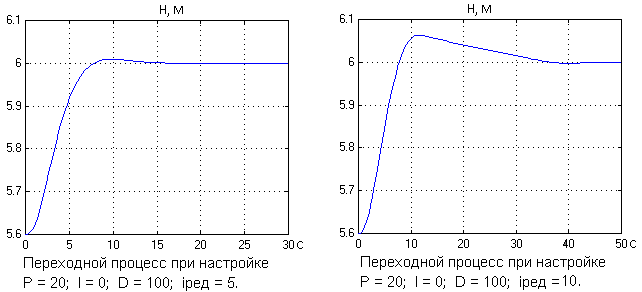
Рисунок 11 – Примеры графиков переходных процессов

Замечания: графики переходных процессов для настроек регулятора из таблицы 2 обязательны и должны быть в тексте курсовой работы!

Таким образом, из таблицы 2 видно, что найдены оптимальные настройки параметров и в окрестности данных параметров лучших нет.

Оптимизация с помощью программы в VisSim

Для выполнения оптимизации в программе необходимо ознакомиться с материалом в фаилах "настройка оптимизации_VS.doc" и "ПРОЧТИ.doc"