Вопросы для самоконтроля

1. Опишите физические явления, наблюдаемые в идеальном конденсаторе в цепи си­нусои­дального тока.

2. Составьте расчётную схему цепи с идеальным генератором и идеальным конденсатором.

3. Запишите математическую связь между мгновенным напряжением, мгновенным током и ёмкостью в идеальном конденсаторе.

4. Объясните физический смысл ёмкостного сопротивления. Как рассчитать ёмкостное сопротивление идеального конденсатора?

5. Сформулируйте и математически запишите закон Ома для максимальных и действующих значений напряже­ния и тока на участке цепи с ёмкостью.

6. Запишите математическое выражение мгновенного тока в ёмкости, приняв начальную фазу равной нулю.

7. Запишите математическое выражение мгновенного напряжения на ёмкости для указанного выше тока.

8. Постройте графически оригиналы мгновенного напряжения и мгновенного тока на участке цепи с ёмкостью.

9. Изобразите напряжение и ток с помощью векторов.

10. Чему равен угол сдвига фаз в ёмкости?

11. Получите математическое выражение мгновенной мощности в ёмкости. С какой частотой колеблется мгновенная мощность в ёмкости?

12. Чему равна активная мощность в ёмкости?

13. Как рассчитать реактивную мощность в ёмкости? Укажите её единицу.

14. Объясните физический смысл реактивной мощности в ёмкости.

Задания для самоконтроля

К идеальному конденсатору подведено напряжение u_с = 282 sin (t + 47) В. Ёмкость конденсатора равна 318 мкФ. Частота тока в цепи f = 50 Гц.

1. Найти реак­тив­ное сопротивление конденсатора.

2. Записать мгновенное значение тока.

3. Найти реактив­ную мощность в ёмкости.

4. Записать выражение мгновенной мощности в ём­кости.

5. Изобразить графически мгновенное напряжение и мгновенную мощность в функции t.

3.5. Реальная катушка в цепи переменного синусоидального тока

Включим катушку в цепь переменного синусоидального тока. Ге­нератор принимаем идеальным, сопротивлением соединительных проводов пренебрегаем. В катушке наблюдаются следующие физические процессы:

• под действием синусоидальной э.д.с. источника в катушке протекает ток i;

• наблюдается тепловое действие тока и катушка нагревается;

• переменный синусоидальный ток создает переменное магнитное поле, кото­рое пронизывает эту же катушку – наблюдается явление электромаг­нитной индукции (самоиндукции) и в катушке наводится э.д.с. самоин­дукции e_L.

Составим расчётную схему катушки (рис.3.19).

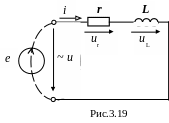Запишем уравнение электрического равновесия для этой цепи:

(3.63) (3.64)

Зададимся током в цепи

(3.65)

и найдём, каким должно быть в этом случае приложенное напряжение u, для чего подставим значение тока в (3.64):

.

(3.66)

Обозначим согласно (3.24) и (3.40)

(3.67) (3.68)

и перепишем уравнение (3.66) в следующем виде:

.

(3.69)

Запишем мгновенное приложенное напряжение в общем виде:

.

(3.70)

Построим векторную диаграмму тока и напряжения этой цепи (рис.3.20).

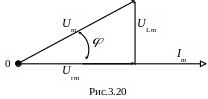
Таким образом, _u = _i +  и мгновенное напряжение на зажимах цепи запи­сывается так:

,

(3.71)

а так как в данном случае _i = 0, то _u =  .

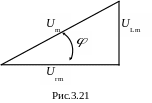
Рассмотрим треугольник напряжений на векторной диаграмме (рис.3.21).

Запишем выражения сторон треугольника:

, , ,

(3.72) (3.73) (3.74)

где r – активное сопротивление катушки, Ом;

x_L – реактивное сопротивление катушки, Ом;

– полное сопротивление ка­тушки

(вводим такое понятие по аналогии с r и х_L), Ом.

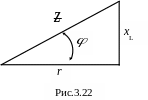
Разделим стороны треугольника напряжений на I_m и получим треугольник сопротивлений (рис.3.22).

Как видно из рисунка, полное сопротивление цепи катушки переменному току

.

(3.75)

Угол сдвига фаз в катушке может быть найден через параметры катушки (r, x_L, ), например:

.

(3.76)

Умножим стороны треугольника сопротивлений на квадрат действующего значения тока и получим треугольник мощностей (рис.3.23).

С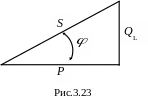 тороны треугольника представляют собой мощности:

активную P = rI2, Вт;	(3.76)
реактивную QL = xLI2, вар;	(3.77)
полную S = I2, ва.	(3.78)

Введём понятие коэффициента мощности, под которым будем понимать от­ношение активной мощности к полной .

Как видно из треугольника мощностей, коэффициент мощности численно ра­вен косинусу угла сдвига фаз, т.е.

.

(3.79)

Таким образом, реальную катушку можно рассматривать одновременно как резистор – с одной стороны и как идеальную катушку – с другой. Все процессы можно описать с помощью двух идеальных элементов – активного сопротивления и индуктивности, описанные в п.3.2 и 3.3.

Пример 3.9

К реальной катушке подведено напряжение u = 282 sin (t + 70) В.

Активное сопротивление катушки равно 3 Ом.

Реактивное сопротивление катушки равно 4 Ом.

Выполнить анализ цепи.

Решение.

1. Определяем полное сопротивление цепи по (3.75):

.

2. Определяем амплитуду тока по (3.74):

.

3. Определяем угол сдвига фаз цепи по (3.76):

.

4. Определяем начальную фазу тока:

_i = _u –  = 70 – 53 = 17.

5. Записываем мгновенный ток:

i = 56,4 sin (t + 17) А.

6. Определяем амплитуду напряжения на активном сопротивлении по (3.72):

U_rm = 356,4 = 169,2 В.

7. Определяем начальную фазу напряжения на активном сопротивлении:

_ur = _i = 17.

8. Записываем мгновенное напряжение на активном сопротивлении:

u_r = 169,2 sin (t + 17) В.

9. Определяем амплитуду напряжения на индуктивном сопротивлении по (3.73):

U_Lm = 456,4 = 225,6 В.

10. Определяем начальную фазу напряжения на индуктивном сопротивлении:

_uL = _i + 90 = 17 + 90 = 107.

11. Записываем мгновенное напряжение на индуктивном сопротивлении:

u_L = 225,6 sin (t + 107) В.

12. Определяем действующее значение тока по (3.14):

.

13. Определяем активную мощность по (3.76):

Р = 340² = 4800 Вт = 4,8 кВт.

14. Определяем реактивную мощность по (3.77):

Q_L = 440² = 6400 вар = 6,4 квар.

15. Определяем полную мощность по (3.78):

S = 540² = 8000 ва = 8,0 ква.

16. Определяем коэффициент мощности катушки по (3.79):

.