
- •Лабораторна робота № 1 цифрова фільтрація вимірювальних сигналів. Нерекурсивні цифрові фільтри (нцф). Фільтр низьких частот
- •1.1. Основні теоретичні відомості
- •1.2. Завдання на лабораторну роботу
- •1.4. Контрольні питання
- •Лабораторна робота № 2 цифрова фільтрація вимірювальних сигналів. Нерекурсивні цифрові фільтри (нцф). Смуговий фільтр
- •2.1. Основні теоретичні відомості
- •2.2. Завдання на лабораторну роботу
- •2.4. Контрольні питання
Лабораторна робота № 1 цифрова фільтрація вимірювальних сигналів. Нерекурсивні цифрові фільтри (нцф). Фільтр низьких частот
Мета роботи - ознайомлення з принципами фільтрації вимірювальних сигналів, реалізація процедури фільтрації з використанням нерекурсивних фільтрів низької частоти.
1.1. Основні теоретичні відомості
Нерекурсивні фільтри реалізують алгоритм згортки двох функцій: yk = hn ③ xk-n, де xk - масив вхідних даних фільтра, hn - оператор (ядро, імпульсний відгук) фільтра, k і n - нумерація числових значень масиву даних і числових значень коефіцієнтів фільтра, k = 0, 1, 2, ..., K; n = 0, 1, 2, ..., N; K ≥ N. Значення вихідних відліків згортки yk для будь-якого аргументу k визначаються поточними і "минулими" (до k-N) значеннями вхідних відліків. Такий фільтр називається нерекурсивним цифровим фільтром (НЦФ). Інтервал [0-N] оператора отримав назву "вікна" фільтра. Вікно фільтра становить N +1 відлік, фільтр є одностороннім каузальним, тобто причинно обумовленим поточними і "минулими" значеннями вхідного сигналу, і вихідний сигнал не випереджає вхідного. У загальному випадку, каузальний фільтр змінює в спектрі сигналу складу гармонік, їх амплітуди і фази.
Каузальний фільтр може бути реалізований фізично в реальному масштабі часу. Початок фільтрації можливо тільки при завданні певних початкових умов - N значень відліків для точок x (k-n) при k <n. Як правило, в якості початкових умов приймаються нульові значення, тренд сигналу або значення відліку х(0), тобто продовження відліку x(0) назад по аргументу.
При обробці даних на ЕОМ обмеження по каузальності знімається. У програмному розпорядженні фільтра можуть перебувати як "минулі", так і "майбутні" (k + n, до k + N ') значення вхідної послідовності відліків щодо поточної точки обчислень k, при цьому для завершення згортки (аналогічно початку) потрібно N' точок кінцевих умов при (k + n)> K. При N'= N і h(-n) = h(n) фільтр називається двостороннім симетричним фільтром. Симетричні фільтри, на відміну від односторонніх, не змінюють фази оброблюваного сигналу.
Основна властивість будь-якого фільтру - його частотна (frequency response) і фазова характеристики. Вони показують, який вплив фільтр робить на амплітуду і фазу різних гармонік оброблюваного сигналу.
До найбільш відомих типів нерекурсивних цифрових фільтрів (НЦФ) відносяться частотні фільтри, алгоритм яких для симетричних НЦФ, не змінюють фазу сигналів, має вигляд:
yk =![]() hn
sk-n.
hn
sk-n.
Типи фільтрів. В залежності від виду частотної характеристики виділяють три основні групи частотних фільтрів: ФНЧ - фільтри низьких частот (low-pass filters) - пропускання низьких і придушення високих частот у вхідному сигналі, ФВЧ - фільтри високих частот (high-pass filters) - пропускання високих і придушення низьких частот, і ПФ - смугові фільтри, які пропускають (band-pass filters) або пригнічують (band-reject filters) сигнал в певній частотній смузі. Серед останніх в окрему групу іноді виділяють РФ - режекторні фільтри, розуміючи під ними фільтри з придушенням певної гармоніки у вхідному сигналі, і СФ - селекторні фільтри, зворотні РФ.
Якщо мова йде про придушення певної смуги частот у вхідному сигналі, то такі фільтри називають загороджувальними. Ні теоретичного, ні практичного інтересу до методів їх розрахунку зазвичай не проявляється, так як їх частотна характеристика зазвичай задається інверсією характеристики смугового фільтра (1- Hп()) і яких-небудь додаткових особливостей при своєму проектуванні не має.
Схематичні частотні характеристики фільтрів наведено на малюнку 1. Між частотними інтервалами пропускання і придушення сигналу існує зона, яка називається перехідною. Ширина перехідної зони визначає різкість характеристики фільтра. У цій зоні амплітудна характеристика монотонно зменшується (або збільшується) від смуги пропускання до смуги придушення (або навпаки).
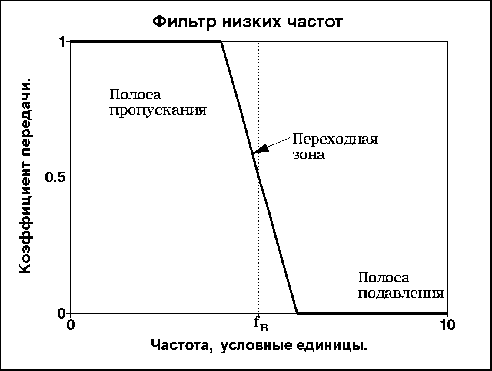
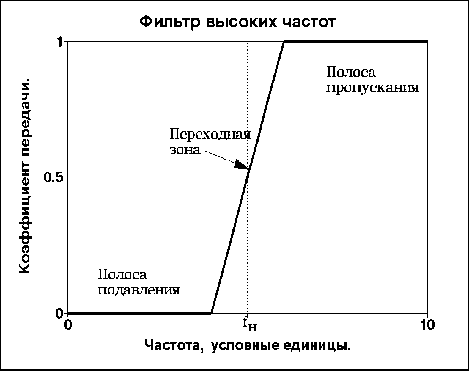
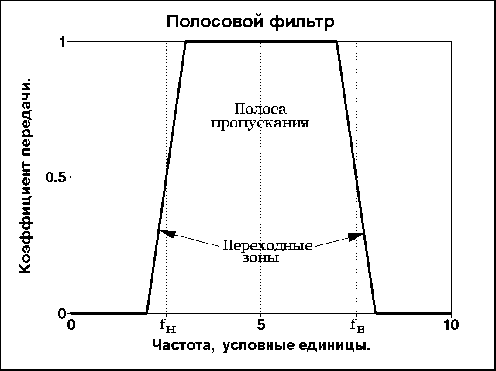
Рис. 1. Типи основних частотних фільтрів.
Практика проектування цифрових фільтрів базується, в основному, на синтезі фільтрів низьких частот. Всі інші види фільтрів можуть бути отримані з фільтрів низьких частот відповідним перетворенням.
Рис. 2.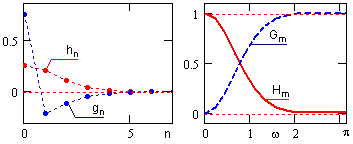
Так, наприклад, фільтр високих частот g(n) може бути отриманий інверсією фільтра низьких частот h (n) - обчисленням різниці між вихідним сигналом і результатом його фільтрації низько-частотних НЦФ:
y(k) = s(k) – h(n) s(k-n).
Звідси, умова інверсії симетричного низькочастотного фільтра в високочастотний:
g(0) = 1-h(0), g(n) = -h(n) при n0.
Приклад звернення і спектри фільтрів наведено на рис. 2 (у правій частині головних діапазонів).
Рис. 3.
Застосовується також спосіб отримання фільтрів високих частот з низькочастотних фільтрів шляхом реверсу частоти в передавальної функції низькочастотного фільтра, тобто заміною змінної на змінну ' = (при t = 1). Для симетричних фільтрів, що містять в передавальної функції тільки косинусні члени аргументу , в результаті такої операції будемо мати:
cos n(-) = cos n cos n = (-1)n cos n.
Останнє означає зміну знака всіх непарних гармонік передавальної характеристики фільтра і, відповідно, всіх непарних членів фільтра:
g (n) = h (n) при n = ± 1, ± 3, ...
Приклад частотного реверсу наведено на рис. 3. Фізичну сутність такої операції інверсії спектра легко зрозуміти на постійної складової сигналу. При зміні на протилежний знак кожного другого відліку постійної величини це постійне значення перетворюється в "пилу", частота якої дорівнює частоті Найквіста головного частотного діапазону (відліки по амплітудним значенням цієї частоти), так само як і навпаки, відліки гармоніки сигналу на частоті Найквіста (Знакозмінні в силу зсуву по інтервалах дискретизації на )) перетворюються на постійну складову.
Смуговий фільтр може реалізуватися послідовним застосуванням ФНЧ і ФВЧ з відповідним перекриттям частот пропускання. В математичному уявленні це означає послідовну згортку масиву даних з масивами коефіцієнтів hн - низькочастотного, і hв - високочастотного фільтрів:
vk = hн(n) ③ s(k-n), yk = hв(n) ③ vk = hн(n) ③ hв(n) ③ s(k-n).
Так як операція згортки коммутативна, то замість окремих масивів коефіцієнтів ФНЧ і ФВЧ їх сверткой може бути визначений безпосередньо масив коефіцієнтів смугового фільтра: hn = hн(n) ③ hв(n).
Смуговий режекторний фільтр також може бути отриманий методом інверсії смугового фільтра. Одночастотні режекторні фільтри звичайно виконуються на основі простих рекурсивних цифрових фільтрів, більш ефективних для даних цілей.
Часто до фільтрів пред'являються більш складні вимоги. Наприклад, фільтр може мати кілька частотних смуг пропускання з різними коефіцієнтами підсилення, а для смуг непропускання можуть бути задані різні коефіцієнти придушення. Іноді необхідна частотна характеристика фільтру задається взагалі довільної кривої.
Методика розрахунків НЦФ. Зазвичай при фільтрації сигналів задається необхідна частотна характеристика фільтру. Завданням є побудувати фільтр, що відповідає заданим вимогам і провести фільтрацію. Найчастіше буває неможливо побудувати в точності заданий фільтр, і виконується фільтр, близьке за характеристиками до заданого.
Існує багато способів побудови фільтрів з заданою частотною характеристикою. Найбільш простий з них - проектування фільтрів з лінійної фазою за допомогою вагових вікон. Цей спосіб є універсальним і дозволяє отримати фільтр з будь-якої заданої частотною характеристикою. Відзначимо, однак, що з допомогою інших, математично більш строгих і досконалих методів, іноді вдається побудувати фільтр меншої довжини, що задовольняє тим самим вимогам до частотній характеристиці.
Найбільш простою є методика розрахунків програмних двосторонніх симетричних фільтрів без зміни фази вихідного сигналу щодо вхідного. У найзагальнішому вигляді вона включає:
1. Завдання ідеальної амплітудно-частотної характеристики передатної функції фільтра. Термін ідеальності розуміється тут в тому сенсі, що на характеристиці зазначаються смуги пропускання і придушення частот з коефіцієнтами передачі 1 і 0 відповідно без перехідних зон.
2. Розрахунок функції імпульсного відгуку ідеального фільтра (зворотне перетворення Фур'є частотної характеристики фільтра). При наявності стрибків функцій на кордонах пропускання/придушення імпульсний відгук містить нескін-ченно велику кількість членів.
3. Обмеження функції відгуку до певної кількості членів, при цьому на передавальної характеристиці фільтра виникає явище Гіббса - осциляції частотної характеристики з центрами на скачках.
4. Для нейтралізації явища Гіббса проводиться вибір ваговій функції і розрахунок її коефіцієнтів, на які множаться коефіцієнти функції відгуку фільтру. Результатом цієї операції є значення коефіцієнтів оператора фільтра (робочий імпульсний відгук фільтра). По суті, операції 3 і 4 являють собою усічення ряду Фур'є динамічного (тимчасового) подання передавальної функції фільтра певної ваговій функцією (множення на вагову функцію).
5. З використанням отриманих значень коефіцієнтів оператора фільтра проводиться побудова його частотної характеристики і перевіряється її відповідність поставленому завданню.
При проектуванні симетричних нерекурсивних фільтрів немає необхідності базуватися на розрахунку фільтрів низьких частот з наступним їх перетворенням, при необхідності, в фільтри верхніх частот смугові фільтри. Розрахунок безпосередньо смугового фільтра досить простий, а НЧ-і ВЧ-фільтри є окремим випадком смугового фільтра з однієї верхньої або однієї нижньої граничною частотою.
