Задача 1.5

В теплообменнике типа «труба в трубе» в кольцевом пространстве охлаждается жидкость от температуры = 98 С до температуры = 30 С. Расход жидкости (20 %-й раствор NaCl) – = 13000 кг/ч. Охлаждающая вода прокачивается по внутренней трубе и нагревается от температуры = 16 С до температуры = 78 С. Теплообменник состоит из = 80 элементов. Размеры труб: наружный = 76 мм и внутренний = 70 диаметры внутренней трубы и наружный = 108 мм и внутренний = 100 мм диаметры внешней трубы. Материал труб – нержавеющая сталь. На стенке внутренней трубы со стороны обеих жидкостей отложился слой загрязнений общей толщиной = 1 мм.

Определить расход охлаждающей воды, поверхность теплообмена и длину каждого элемента. Нарисовать эскиз аппарата.

Примечание: коэффициент теплопроводности накипи принять равным

2,5 Вт/(мК) (см. таблицу 7).

Решение

1. Рассчитаем площадь поверхности теплообмена аппарата из основного кинетического уравнения теплопередачи:

,

где – коэффициент теплопередачи от пара к нагреваемой жидкости, Вт/м²·К;

– средняя разность температур между теплоносителями, С;

– тепловая нагрузка теплообменника, Вт, рассчитаем по уравнению:

Вт,

где – удельная теплоемкость охлаждаемой жидкости (20 %-й раствор NaCl), Дж/кг∙К, определяется по ее средней температуре

⁰С по формуле [1, стр. 22]:

Дж/кг·К,

где – удельная теплоемкость соли NaCl, Дж/кг∙К, [1, табл. 3];

– удельная теплоемкость воды, Дж/кг∙К, определяется по из таблицы свойств воды [1, табл. 1];

– концентрация растворенной соли в растворе.

Для расчета средней разности температур (движущей силы теплопередачи) построим график изменения температур теплоносителей вдоль поверхности теплообменника. Схему движения теплоносителей выберем противоточную, как имеющую преимущества перед прямоточной (приложение Б, рисунок 4).

Рассчитаем большую и меньшую разность температур теплоносителей на концах теплообменника:

⁰С,

⁰С.

Рассчитаем значение отношения:

< 2,

поэтому рассчитаем среднюю разность температур по формуле

⁰С.

Коэффициент теплопередачи от охлаждаемой жидкости к холодной воде рассчитаем по уравнению аддитивности термических сопротивлений:

,

где – толщина стенки труб, м, рассчитаем по выражению:

мм или 0,003 м,

= 17 Вт/м·К и = 2,5 Вт/м·К – коэффициенты теплопроводности материала труб (нержавеющая сталь) и слоя загрязнений [1, табл. 7];

и – коэффициенты теплоотдачи от горячего теплоносителя (20 % раствор NaCl) к стенке трубы и от стенки трубы к холодному теплоносителю (воде), Вт/м²·К.

Коэффициент теплоотдачи от охлаждаемой жидкости к стенке трубы рассчитаем по выражению:

,

где – критерий Нуссельта;

= м – определяющий геометрический размер;

– коэффициент теплопроводности охлаждаемой жидкости (20 %-й раствор NaCl), Вт/м∙К, определяется при ее средней температуре по формуле [1, стр. 23]:

Вт/м∙К,

где – коэффициент теплопроводности воды при = 64 ⁰С [1, табл. 1];

– концентрация раствора NaCl, % масс.

Вид критериального уравнения для расчета зависит от режима течения охлаждаемой жидкости по кольцевому зазору, который определяется значением критерия Рейнольдса . Критерий Рейнольдса рассчитаем по формуле

,

где – скорость течения охлаждаемой жидкости по кольцевому зазору между наружной и внутренней трубами, м/с, определяем из уравнения расхода:

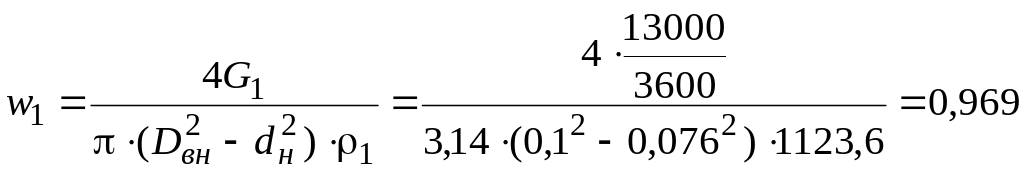м/с,

где – плотность охлаждаемой жидкости (20 %-й раствор NaCl), кг/м³, определяется по ее средней температуре = 64 ⁰С из [1, табл. 8];

– кинематическая вязкость охлаждаемой жидкости, м²/с, определяется по ее средней температуре по формуле

м²/с,

где – динамическая вязкость охлаждаемой жидкости (20 % раствор NaCl), МПа∙с, определяем по ее средней температуре из [1, табл. 9].

,

>10000, поэтому режим течения жидкости в кольцевом зазоре – турбулентный, значение критерия Нуссельта рассчитывается по критериальному уравнению

,

где – критерий Прандтля:

,

Вт/м²·К.

Коэффициент теплоотдачи от стенки трубы к холодной воде рассчитаем по выражению:

,

где – критерий Нуссельта;

= = 0,07 м;

– коэффициент теплопроводности воды, Вт/м∙К, определяется при ее средней температуре ⁰С по таблице свойств воды [1, табл. 1].

Вид критериального уравнения для расчета зависит от режима течения воды по внутренней трубе, который определяется значением критерия Рейнольдса . Критерий Рейнольдса рассчитаем по формуле

,

где – кинематическая вязкость воды, м²/с, определяем по = 47 ⁰С из таблицы свойств воды [1, табл. 1];

– скорость течения воды по внутренней трубе, м/с, определяем из уравнения расхода:

м/с,

где – плотность горячей воды, кг/м³, определяется по ее средней температуре = 47 ⁰С из таблицы свойств воды [1, табл. 1].

– расход горячей воды, кг/с, определим из уравнения теплового баланса теплообменника:

кг/с,

где – тепловая нагрузка теплообменника, Вт;

– удельная теплоемкость воды, Дж/кг∙К, определяется по из [1, табл. 1].

,

>10000, поэтому режим течения жидкости в трубах – турбулентный, значение критерия Нуссельта рассчитывается по критериальному уравнению

,

где – критерий Прандтля:

,

Вт/м²·К,

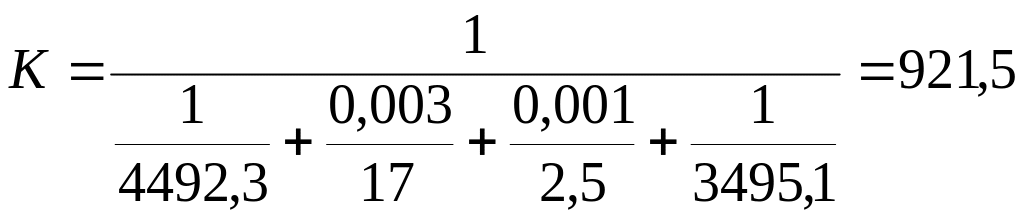Вт/м²·К,

м².

2. Рассчитаем суммарную длину всех элементов теплообменника :

м,

где = , при > .

3. Рассчитаем длину одного элемента теплообменника по формуле:

м.

Ответ. кг/с; м²; м.

Эскиз теплообменника типа «труба в трубе» для охлаждения 20 %-го раствора NaCl приведен в приложении В, рисунок 6.