
- •Примеры решения задач контрольной работы № 1 на темы «Теплообмен» и «Выпаривание»
- •Содержание
- •Введение
- •Примеры решения задач на тему «Теплообмен» Задача 1.1
- •Решение
- •Задача 1.2
- •Решение
- •Задача 1.3
- •Решение
- •Задача 1.4
- •Решение
- •Задача 1.5
- •Решение
- •Примеры решения задач на тему «Выпаривание» Задача 2.1
- •Решение
- •Задача 2.2
- •Решение
- •Задача 2.3
- •Решение
- •Задача 2.4
- •Решение
- •Задача 2.5
- •Решение
- •Список литературы
- •Приложение а (обязательное)
- •Приложение б (обязательное)
- •Приложение в (обязательное)
- •Приложение г (обязательное)
- •Примеры решения задач контрольной работы № 1 на темы «Теплообмен» и «Выпаривание»
Задача 1.4
В теплообменнике
типа «труба в трубе» в кольцевом
пространстве нагревается жидкость (20
%-й раствор сахара) от температуры
=
20 С
до температуры
=
80 С.
Расход жидкости –
=
12000 кг/ч. Горячая вода прокачивается по
внутренней трубе и охлаждается от
температуры
![]() =
95 С
до температуры
=
30 С.
Размеры труб: наружный
=
76 мм, и внутренний
=
95 С
до температуры
=
30 С.
Размеры труб: наружный
=
76 мм, и внутренний
![]() =
70 мм, диаметры внутренней трубы и наружный
=
108 мм, и внутренний
=
70 мм, диаметры внутренней трубы и наружный
=
108 мм, и внутренний
![]() =
100 мм, диаметры наружной трубы. Материал
– черная сталь. На стенке внутренней
трубы с обеих сторон отложился слой
загрязнений общей толщиной
=
0,4 мм. Потери теплоты в окружающую среду
составляют 2% от теплоты, полученной
жидкостью.
=
100 мм, диаметры наружной трубы. Материал
– черная сталь. На стенке внутренней
трубы с обеих сторон отложился слой
загрязнений общей толщиной
=
0,4 мм. Потери теплоты в окружающую среду
составляют 2% от теплоты, полученной
жидкостью.
Определить расход
горячей воды, количество элементов,
если длина одного элемента
![]() равна 5,0 м. Нарисовать эскиз аппарата.
равна 5,0 м. Нарисовать эскиз аппарата.
Решение
1. Рассчитаем площадь поверхности теплообмена аппарата из основного кинетического уравнения теплопередачи:
![]() ,
,
где – коэффициент теплопередачи от пара к нагреваемой жидкости, Вт/м2·К;
– средняя разность температур между теплоносителями, С;
– тепловая нагрузка теплообменника, Вт:
![]() Вт,
Вт,
где 1,02 – коэффициент, учитывающий 2% потери теплоты (по условию задачи);
–
удельная теплоемкость
20 %-го сахарного раствора, определяется
по его средней температуре
![]() 0С
и концентрации
=
20 % из [1, стр. 22]:
0С
и концентрации
=
20 % из [1, стр. 22]:
![]() Дж/кг·К,
Дж/кг·К,
где = .
Для расчета средней разности температур (движущей силы теплопередачи) построим график изменения температур теплоносителей вдоль поверхности теплообменника для противоточной схемы движения теплоносителей (приложение Б, рисунок 4).
Рассчитаем большую и меньшую разности температур теплоносителей на концах теплообменника:
![]() 0С,
0С,
![]() 0С.
0С.
Рассчитаем значение отношения:
![]() < 2, поэтому
рассчитаем
по упрощенной формуле
< 2, поэтому
рассчитаем
по упрощенной формуле
![]() 0С.
0С.
Коэффициент теплопередачи от горячего теплоносителя к нагреваемой жидкости рассчитаем по уравнению аддитивности термических сопротивлений:
,
где – толщина стенки труб, м:
![]() мм = 0,003 м,
мм = 0,003 м,
= 45 Вт/м·К и = 2,5 Вт/м·К – коэффициенты теплопроводности материала труб (черная сталь) и слоя загрязнений [1, табл. 7];
и – коэффициенты теплоотдачи от горячего теплоносителя к стенке трубы и от стенки трубы к нагреваемой жидкости, Вт/м2·К.
Коэффициент теплоотдачи от горячей воды к стенке трубы рассчитаем повыражению:
![]() ,
,
где
![]() –
критерий Нуссельта;
–
критерий Нуссельта;
![]() =
=
0,07 м – определяющий геометрический
размер;
=
=
0,07 м – определяющий геометрический
размер;
![]() –
коэффициент
теплопроводности воды, Вт/м∙К, определяется
при ее средней температуре
–
коэффициент
теплопроводности воды, Вт/м∙К, определяется
при ее средней температуре
![]() 0С
по таблице свойств воды [1, табл. 1].
0С
по таблице свойств воды [1, табл. 1].
Вид критериального
уравнения для расчета
зависит от режима течения жидкости по
трубам, который определяется значением
критерия Рейнольдса
![]() .
Критерий Рейнольдса рассчитаем по
формуле:
.
Критерий Рейнольдса рассчитаем по
формуле:
![]() ,
,
где
![]() –
кинематическая вязкость воды, м2/с,
определяем по
–
кинематическая вязкость воды, м2/с,
определяем по
![]() из таблицы свойств воды [1, табл. 1];
из таблицы свойств воды [1, табл. 1];
![]() –
скорость течения
горячей воды по внутренней трубе, м/с,
определяем из уравнения расхода:
–
скорость течения
горячей воды по внутренней трубе, м/с,
определяем из уравнения расхода:
![]() м/с,
м/с,
где
![]() – плотность горячей воды, кг/м3,
определяется по ее средней температуре
=62,5
0С
из таблицы свойств воды [1, табл. 1];
– плотность горячей воды, кг/м3,
определяется по ее средней температуре
=62,5
0С
из таблицы свойств воды [1, табл. 1];
![]() –
расход горячей
воды, кг/с, определим из уравнения
теплового баланса теплообменника:
–
расход горячей
воды, кг/с, определим из уравнения
теплового баланса теплообменника:
![]() кг/с,
кг/с,
где – тепловая нагрузка теплообменника, Вт;
![]() –
удельная теплоемкость
воды, Дж/кг∙К, определяется по
из [1, табл. 1].
–
удельная теплоемкость
воды, Дж/кг∙К, определяется по
из [1, табл. 1].
![]()
>10000, поэтому режим течения жидкости в трубах – турбулентный, критерий Нуссельта рассчитывается по критериальному уравнению:
![]() ,
,
где
![]() –
критерий Прандтля:
–
критерий Прандтля:
![]() ,
,
![]() Вт/м2·К,
Вт/м2·К,
Коэффициент теплоотдачи от стенки трубы к нагреваемой жидкости рассчитаем по критериальному уравнению:
![]() ,
,
где
![]() –
критерий Нуссельта;
–
критерий Нуссельта;
![]() =
=
![]() м
– определяющий геометрический размер
кольцевого зазора;
м
– определяющий геометрический размер
кольцевого зазора;
![]() –
коэффициент
теплопроводности нагреваемой жидкости
(20%-й раствор сахара), Вт/м∙К, определяется
при ее средней температуре
по
формуле [1, стр. 24]:
–
коэффициент
теплопроводности нагреваемой жидкости
(20%-й раствор сахара), Вт/м∙К, определяется
при ее средней температуре
по
формуле [1, стр. 24]:
![]() Вт/м∙К,
Вт/м∙К,
где
![]() – коэффициент теплопроводности воды
при
– коэффициент теплопроводности воды
при
![]() 0С
[1, табл. 1];
0С
[1, табл. 1];
– поправочный коэффициент [1, табл. 6];
– концентрация сахарного раствора, % масс.
Рассчитаем значение
критерия Рейнольдса для нагреваемой
жидкости
![]() по формуле
по формуле
![]() ,
,
где
![]() –
скорость течения нагреваемой жидкости
по кольцевому зазору между наружной и
внутренней трубами, м/с, определяем из
уравнения расхода:
–
скорость течения нагреваемой жидкости
по кольцевому зазору между наружной и
внутренней трубами, м/с, определяем из
уравнения расхода:
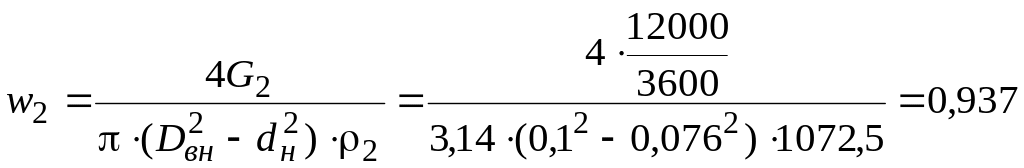 м/с,
м/с,
где
![]() – плотность нагреваемой жидкости (20
%-й сахарный раствор), кг/м3,
определяется по ее средней температуре
=
50 0С
из [1, табл. 8].
– плотность нагреваемой жидкости (20
%-й сахарный раствор), кг/м3,
определяется по ее средней температуре
=
50 0С
из [1, табл. 8].
![]() –
кинематическая
вязкость нагреваемой жидкости, м2/с
при ее средней температуре
–
кинематическая
вязкость нагреваемой жидкости, м2/с
при ее средней температуре
![]() ,
м2/с
,
м2/с
где
![]() –
динамическая вязкость нагреваемой
жидкости (20 %-й раствор сахара), МПа∙с,
определяем по
из [1, табл. 9].
–
динамическая вязкость нагреваемой
жидкости (20 %-й раствор сахара), МПа∙с,
определяем по
из [1, табл. 9].
![]() .
.
>10000, поэтому режим течения жидкости в кольцевом зазоре – турбулентный, поэтому критерий Нуссельта рассчитывается по критериальному уравнению
![]() ,
,
где
![]() –
критерий Прандтля:
–
критерий Прандтля:
![]() ,
,
![]() Вт/м2·К,
Вт/м2·К,
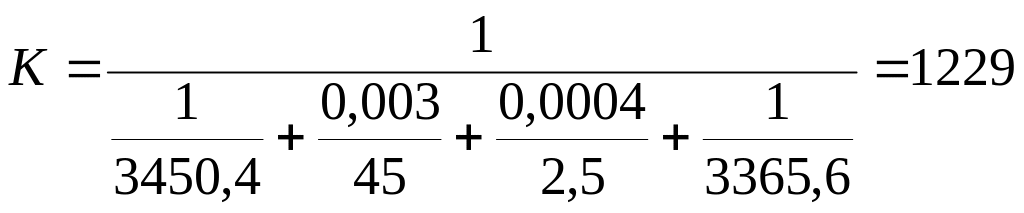 Вт/м2·К,
Вт/м2·К,
![]() м2.
м2.
2. Рассчитаем общую длину труб теплообменника :
![]() м,
м,
где = , так как > .
3. Рассчитаем число элементов в теплообменнике :
![]() шт.
шт.
Ответ.
![]() кг/с;
кг/с;
![]() шт.
шт.
Эскиз теплообменника типа «труба в трубе» для нагревания 20 %-го раствора сахара приведен в приложении В, рисунок 5.
