Вариант 12

1. Для поражения цели необходимо попасть в нее дважды. Вероятность первого попадания равна 0,2, затем она не меняется при промахах, но после первого попадания увеличивается вдвое. Найти вероятность того, что цель будет поражена первыми двумя выстрелами. 0,08

2. Группа студентов состоит из 5 отличников, 12 хорошо успевающих и 4 занимающихся слабо. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найдите вероятность того, что он получит хорошую или отличную оценку.

3. В продукции некоторого производства брак составляет 15%. Изделия отправляются потребителям (без проверки) в коробках по 100 штук. Найдите вероятности событий:

В – наудачу взятая коробка содержит 13 бракованных изделий;

С – число бракованных изделий в коробке не превосходит 20.

4. Вероятность попадания стрелком в цель равна 0,7. Сделано 25 выстрелов. Определите наивероятнейшее число попаданий в цель и вероятность этого события.

5. В урне 6 белых и 4 черных шара. Из нее пять раз подряд извлекают 1 шар и возвращают назад и перемешивают.Приняв за случайную величину Х число извлеченных белых шаров, составьте ряд распределения Х, найдите М(Х)и D(X).

6. Непрерывная случайная величина задана интегральной функцией F(x). Найдите а) вероятность попадания случайной величины в интервал(1;2); б) дифференциальную функцию f(x); в) M(x), D(x), F(x)=

7. Автомат изготовляет шарики. Шарик считается годным, если отклонение X диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная величина X распределена нормально со средним квадратическим отклонением а = 0,4 мм. Найдите, сколько в среднем, будет годных шариков среди ста изготовленных.

8. Телефонная станция обслуживает 2000 абонентов, в час пик каждый абонент использует связь в среднем в течение 2 минут, т.е. мы считаем, что абонент с вероятностью 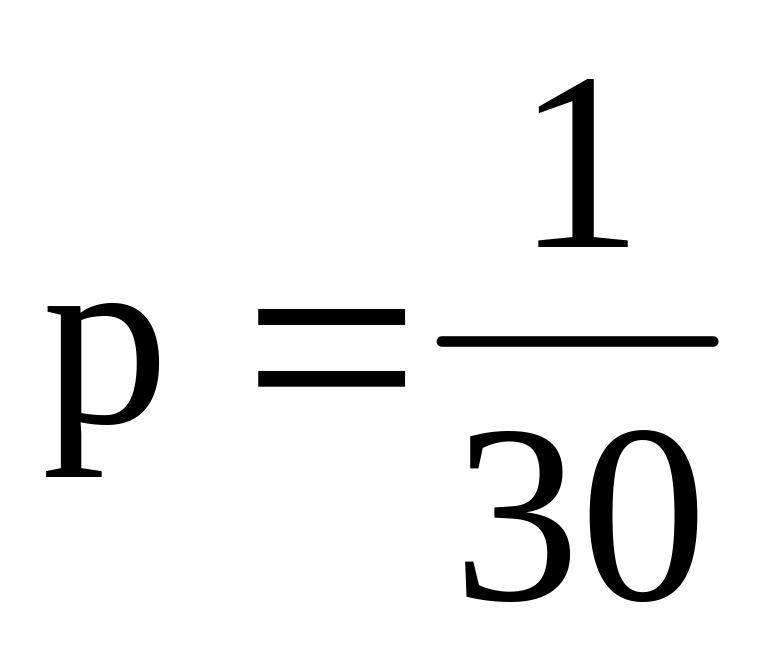использует связь. Какое наименьшее число линий необходимо, чтобы только один из 100 вызовов получал отказ? 86 линий

9. Автомат штампует детали. Контролируется длина детали X, которая распределена нормально с математическим ожиданием (проектная длина), равным 50 мм. Фактически длина изготовленных деталей не менее 32 и не более 68 мм. Найдите вероятность того, что длина наудачу взятой детали больше 55 мм.

10. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением = 20 мм и математическим ожиданием а = 0. Найдите вероятность того, что из трех независимых измерений ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм.

Вариант 13

1. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найдите вероятность того, что откажут не менее четырех элементов.

2. Для приема зачета преподаватель приготовил 50 задач: 20 задач по дифференциальному и 30 задач по интегральному исчислению. Для получения зачета студент должен решить первую попавшуюся ему задачу. Какова вероятность для студента получить зачет, если он знает решение 18 задач по дифференциальному и 15 по интегральному исчислению?

3. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найдите вероятность того, что случайно купленная новая продукция окажется высшего сорта.

4. Вероятность рождения мальчика в регионе составляет р = 0.51. Какова вероятность того, что из 500 новорожденных в регионе мальчиков не менее 250?

5. Тест по теории вероятностей состоит из 10 вопросов. На каждый вопрос в тесте предлагается 4 варианта ответа, из которых надо выбрать один правильный. Какова вероятность того, что, совершенно не готовясь к тесту, студенту удастся угадать правильные ответы по крайней мере на 6 вопросов?

6. Три стрелка делают по одному выстрелу в мишень. Вероятности попадания равны 0,6; 0,7; 0,8 соответственно. Составьте ряд распределения числа попаданий в мишень. Найдите математическое ожидание и дисперсию.

7. Найдите математическое ожидание, дисперсию, медиану и моду непрерывной случайной величины Х, заданной плотностью распределения.

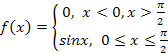
8. Устройство состоит из 100 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,03. Оцените вероятность того, что абсолютная величина разности между числом (математическим ожиданием) отказов за время Т окажется не меньше двух.

9. Случайная величина распределена нормально. Математическое ожидание и среднее квадратическое отклонение соответственно равны 20 и 10. Найдите вероятность того, что отклонение по абсолютной величине будет меньше трёх.

10. Изготовлена партия деталей. Среднее значение длины детали равно 50 см, а среднее квадратическое отклонение равно 0,2 см. Оцените снизу вероятность того, что длина наудачу взятой детали окажется не менее 49,5 см и не более 50,5 см

    Вариант 14

1. Найдите вероятность попадания в паутину бабочки оказавшейся в колодце различной формы?

2. Имеются две урны: в первой 5 белых шаров и 7 черных; во второй 4 белых и 6 черных. Из первой урны во вторую перекладывают, не глядя, один шар. После этого из второй урны берут один шар. Найдите вероятность того, что этот шар будет белым.

3. Проверкой установлено, что 96% изделий служат не меньше гарантируемого срока. Наугад выбирают 15000 изделий. Найдите вероятность того, что со сроком службы менее гарантируемого будет от 570 до 630 изделий.

4. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найдите вероятность того, что откажут:

а) три элемента; б) не менее четырех элементов; в) хотя бы один элемент.

5. Три экзаменатора принимают экзамен по некоторой дисциплине у группы в 30 человек, причем первый опрашивает 6 студентов, второй — 3 студента, а третий — 21 студентов (выбор студентов производится случайным образом из списка). Отношение трех экзаменаторов к слабо подготовившимся различное: шансы таких студентов сдать экзамен у первого преподавателя равны 40%, у второго — только 10%, у третьего — 70%. Известно, что студент сдавал экзамен, но получил «неудовлетворительно». Кому из трех преподавателей вероятнее всего он отвечал?

6. Составьте ряд распределения числа девочек в семье их четырех детей, если вероятность рождения мальчика равна 0,515. Найдите математическое ожидание и дисперсию.

7. Непрерывная случайная величина X задана функцией распределения:

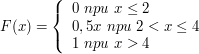
Найдите : а) вероятность того, что в результате испытания X примет значение меньшее 0,2; б) математическое ожидание, дисперсию, медиану и моду непрерывной случайной величины Х

8. Выведите формулу для дисперсии случайной непрерывной величины, имеющей нормальное распределение.

9. Проведённое исследование показало, что вклады населения в данном банке могут быть описаны случайной величиной , распределённой по нормальному закону с параметрами , . Найдите средний размер вклада.

10. Дисперсия каждой из 1000 независимых случайных величин x_k (k = 1, 2,..., 1000) равна 4. Оцените вероятность того, что отклонение средней арифметической этих величин от средней арифметической их математических ожиданий по абсолютной величине не превзойдет 0,1.