Вариант 4

1. Из отрезка [0, 2] на удачу выбраны два числа х и у. Найдите вероятность того, что эти числа удовлетворяют неравенствам х²≤4у≤4х.

2. Три электрических лампочки последовательно включены в цепь. Вероятность того, что одна любая лампочка перегорит, если напряжение в цепи превысит номинальное, равна 0,6. Найдите вероятность того, что при повышенном напряжении тока в цепи не будет.

3. Определите вероятность того, что в семье, имеющей 5 детей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.

4. Имеются две урны: в первой 5 белых шаров и 7 черных; во второй 4 белых и 6 черных. Из первой урны во вторую перекладывают, не глядя, один шар. После этого - из второй урны берут один шар. Найдите вероятность того, что этот шар будет белым.

5. В связке из 3 ключей только один ключ подходит к двери. Ключи перебирают до тех пор, пока не найдется подходящий ключ. Постройте ряд распределения случайной величины X – числа перепробованных ключей. Постройте полигон распределения.

6. Даны ряды распределения двух независимых случайных величин:

			xi		0			2			4
			pi		0,5			0,2			0,3

yj	-2	0	2
pj	0,1	0,6	0,2

Найдите ряд распределения случайной величины Z=X-Y, ее дисперсию.

7. Случайная величина Х задана функцией распределения F(x):

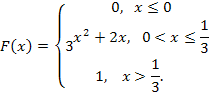
Найдите: а) плотность распределения вероятностей, б) математическое ожидание, дисперсию, среднее квадратичное отклонение, медиану и моду случайной величины Х; в) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу (1/6; 1/3).

8. Найдите функцию распределения случайной величины Х, распределенной равномерно на отрезке [a,b].(вывести формулу)

9. На станке изготавливается некоторая деталь. Ее длина Х - случайная величина, распределенная по нормальному закону со средним значением 20 см и дисперсией 0,2. Найдите вероятность того, что длина детали отклонится от средней длины менее, чем на 0,3?

10. Автомат изготавливает шарики. Шарик считается годным, оклонение Х диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная величина распределена нормально с параметрами а=0 и 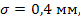. Найдите сколько, в среднем, будет годных шариков среди 100 изготовленных.

Вариант 5

1. В коробке лежат 5 синих, 4 красных, 3 зеленых карандаша. Наудачу вынимают 3 карандаша. Найдите вероятность того, что это будут карандаши разного цвета.

2. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найдите вероятность того, что в цель попали не менее трех раз.

3. Известно, что в среднем, 95% выпускаемой продукции удовлетворяют стандарту. Упрощенная схема контроля признает пригодной продукцию с вероятностью 0,98, если она стандартна, и с вероятностью 0,06, если она не стандартна. Какова вероятность того, что взятое наудачу изделие пройдет упрощенный контроль.

4. Учитель проверяет в среднем за четверть 500 тетрадей. Вероятность того, что он допустит ошибку при проверке тетради, равна 0,008. Определите вероятность того, что учитель допустит ошибку при проверке 5 тетрадей.

5. Три пассажира наугад рассаживаются в двух вагонах. Найдите ряд распределения числа пассажиров, севших в первый вагон. Вычислите математическое ожидание и дисперсию этой случайной величины.

6. Найдите математическое ожидание случайной величины Z = 4X-2Y, если известны математические ожидания M(X) = 5, M(Y) = 3.

7. Задана непрерывная случайная величина Х функцией распределения F(Х). Найдите :

1. плотность распределения вероятностей f(x), постройте ее график;

2. математическое ожидание, дисперсию и среднее квадратическое отклонение, моду и медиану непрерывной случайной величины Х.

3. вероятность того, что Х примет значение из интервала (- )

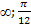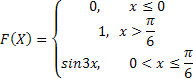
8. Найдите дисперсию случайной величины Х, равномерно распределенной в интервале (a,b).(вывести формулу)

9. Полагая, что рост мужчин определённой возрастной группы есть нормально распределённая случайная величина с параметрам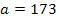и и 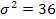. Найдите

функцию плотности вероятности и функцию распределения случайной величины .

10. Оцените вероятность того, что в результате подбрасывания игральной кости в течении 320 раз относительная частота появления на верхней грани пяти очков отклонится от вероятности этого события (по абсолютной величине) не более чем на 0,03.