http://vk.com/reshu_toe
Вариант 537.
Исходные данные: E1=80 В; R1=20 Ом; R4=25 Ом; E2=30 В; R2=5 Ом; R5=40 Ом; E3=45 В; R3=5 Ом; R6=25 Ом;
ЗАДАНИЕ №1.
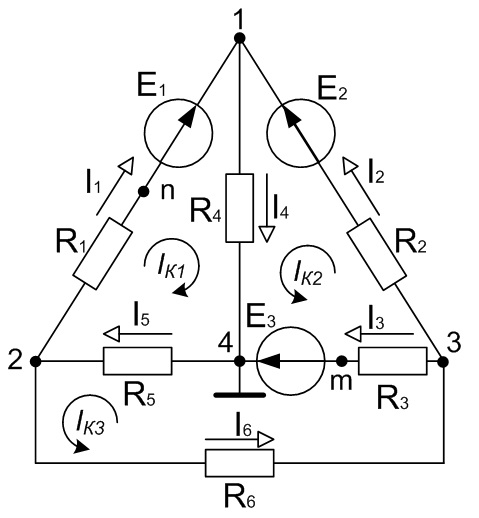
1.1 Метод уравнений Кирхгофа.
По первому закону Кирхгофа:
1 узел: I1 + I2 - I4=0 2 узел: I5 - I1 - I6=0 3 узел: I6 - I2 - I3=0
По второму закону Кирхгофа:
1 контур: E1 = I1·R1 + I4·R4 + I5·R5 2 контур: E2 - E3 = I2·R2 + I4·R4 - I3·R3 3 контур: E3 = I3·R3 + I5·R5 + I6·R6
http://vk.com/reshu_toe
1.2 Метод узловых потенциалов.
Принимаем потенциал узла №4 равным нулю. Рассчитаем проводимости по формуле G=1/R:
G1 = 1/20 Ом = 0.05 См; G2 = 1/5 Ом = 0.2 См; G3 = 1/5 Ом = 0.2 См; G4 = 1/25 Ом = 0.04 См; G5 = 1/40 Ом = 0.025 См; G6 = 1/25 Ом = 0.04 См;
Используя правило для расчета цепей по методу узловых потенциалов, составим систему уравнений:
{ |
φ1·(G1+G2+G4) - φ2·G1 - φ3·G2 = E1·G1 + E2·G2 |
φ2·(G1+G5+G6) - φ1·G1 - φ3·G6 = - E1·G1 |
|
φ3·(G2+G3+G6) - φ1·G2 - φ2·G6 = - E2·G2 - E3·G3 |
Подставляем в уравнения значения проводимостей и ЭДС, получаем:
{ |
0.29·φ1 - 0.05·φ2 - 0.2·φ3 = 10 |
-0.05·φ1 + 0.115·φ2 - 0.04·φ3 = -4 |
|
-0.2·φ1 - 0.04·φ2 + 0.44·φ3 = -15 |
Составим матрицу для решения, и вычислим значения узловых потенциалов с помощью ЭВМ.
( |
0.29 |
-0.05 |
-0.2 |
) |
= |
( |
10 |
) |
-0.05 |
0.115 |
-0.04 |
-4 |
|||||
-0.2 |
-0.04 |
0.44 |
-15 |
Получаем:
φ1 = -0.649 В; φ2 = -48.56 В; φ3 = -38.8 В; φ4 = 0 В.
Зная потенциалы всех узлов, находим токи в каждой цепи.
I1 = (φ2 - φ1 + E1) / R1 = ((-48.56) - (-0.649) + 80) / 20 = 1.604 A; I2 = (φ3 - φ1 + E2) / R2 = ((-38.8) - (-0.649) + 30) / 5 = -1.63 A; I3 = (φ3 - φ4 + E3) / R3 = ((-38.8) - 0 + 45) / 5 = 1.24 A; I4 = (φ1 - φ4) / R4 = ((-0.649) - 0) / 25 = -0.026 A; I5 = (φ4 - φ2) / R5 = (0 - (-48.56)) / 40 = 1.214 A; I6 = (φ2 - φ3) / R6 = ((-48.56) - (-38.8)) / 25 = -0.39 A;
http://vk.com/reshu_toe
1.3 Проверка расчета токов.
Делаем проверку рассчитанных токов по I закону Кирхгофа:
1 узел: I1 + I2 - I4 = 1.604 + (-1.63) - (-0.026) = 0 2 узел: I5 - I1 - I6 = 1.214 - 1.604 - (-0.39) = 0 3 узел: I6 - I2 - I3 = (-0.39) - (-1.63) - 1.24 = 0
Составим баланс мощностей:
∑Pпр = I12·R1 + I22·R2 + I32·R3 + I42·R4 + I52·R5 + I62·R6 = 1.6042·20 + (-1.63)2·5 + + 1.242·5 + (-0.026)2·25 + 1.2142·40 + (-0.39)2·25 = 135.24 Вт; ∑Pист = E1·I1 + E2·I2 + E3·I3 = 80·1.604 + 30·(-1.63) +45·1.24 = 135.24 Вт;
Абсолютная погрешность:
Δ = 135.24 - 135.24 = 0 Вт.
1.4 Расчет методом контурных токов.
Для выбранных контурных токов записываем уравнения по второму закону Кирхгофа.
{ |
Ik1·(R1 + R4 + R5) + Ik2·R4 + Ik3·R5 = E1 |
Ik2·(R2 + R4 + R3) + Ik1·R4 - Ik3·R3 = E2 - E3 |
|
Ik3·(R3 + R5 + R6) + Ik1·R5 - Ik2·R3 = E3 |
http://vk.com/reshu_toe
Подставляем в уравнения значения сопротивлений ветвей и ЭДС, получаем:
{ |
85·Ik1 + 25·Ik2 + 40·Ik3 = 80 |
25·Ik1 + 35·Ik2 - 5·Ik3 = -15 |
|
40·Ik1 - 5·Ik2 + 70·Ik3 = 45 |
Составим матрицу для решения, и вычислим значения контурных токов с помощью ЭВМ.
( |
85 |
25 |
40 |
) |
= |
( |
80 |
) |
25 |
35 |
-5 |
-15 |
|||||
40 |
-5 |
70 |
45 |
Получаем:
Ik1 = 1.604 А; Ik2 = -1.63 А; Ik3 = -0.39 А.
Определяем действительные токи ветвей:
I1 = Ik1 = 1.604 А; I2 = Ik2 = -1.63 А; I3 = Ik3 - Ik2 = 1.24 А; I4 = Ik1 + Ik2 = -0.026 А; I5 = Ik1 + Ik3 = 1.214 А; I6 = Ik3 = -0.39 А.
Результаты расчетов токов ветвей двумя способами сведем в таблицу.
|
I1, A |
I2, A |
I3, A |
I4, A |
I5, A |
I6, A |
Метод узловых потенциалов |
1.604 |
-1.63 |
1.24 |
-0.026 |
1.214 |
-0.39 |
Метод контурных токов |
1.604 |
-1.63 |
1.24 |
-0.026 |
1.214 |
-0.39 |
http://vk.com/reshu_toe
ЗАДАНИЕ №2.
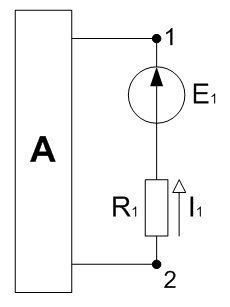
Методом эквивалентного генератора определить ток в ветви №1.
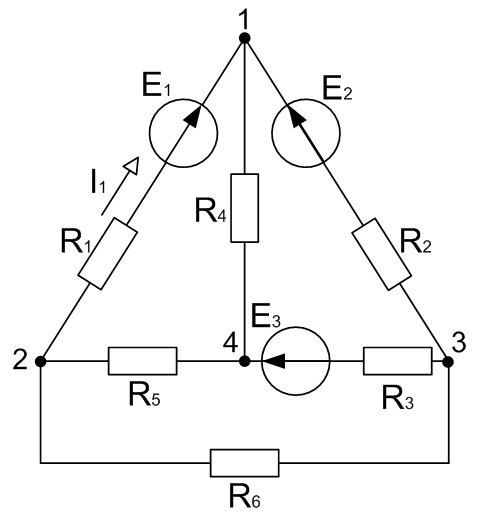
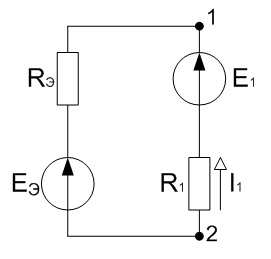
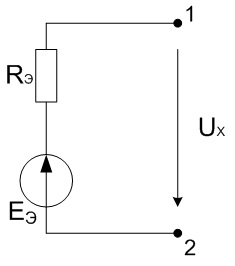
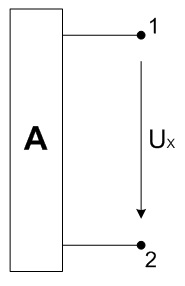
Удалим из цепи первую ветвь, а оставшуюся ее часть представляем в виде активного двухполюсника, который в свою очередь заменяем эквивалентным генератором.
|
|
|
|
