Нахождение области определения суммы, произведения и разности функций.

Область определения суммы функций.

Если функция f - это сумма n функций (основных элементарных или элементарных) f₁, f₂, …, f_n, то есть, функция f задается формулой , то областью определения функции f является пересечение областей определения функций f₁, f₂, …, f_n. Итак, .

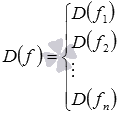Пример.

Найдите область определения функции .

Решение.

Функция f представлена суммой четырех функций: f₁ - степенной функции с показателем 7, f₂ - степенной функцией с показателем 1, f₃ - постоянной функцией и f₄ - функцией тангенс.

Мы знаем, что , а областью определения тангенса является множество всех действительных чисел, кроме чисел .

Область определения функции f – это пересечение областей определения функций f₁, f₂, f₃ и f₄, а это есть множество всех действительных чисел, за исключением чисел .

Ответ:

множество всех действительных чисел, кроме чисел .

Пример.

Найдите область определения функции .

Решение.

В этом примере функция f есть сумма трех функций: f₁ – степенная функция с показателем , f₂ – показательной функции с основанием 2 и сложной функции f₃, которой соответствует формула , где f₄ – функция арккосинус, а f₅ - котангенс.

Областью определения функции f является пересечение множеств и .

Так как нам известны области определения основных элементарных функций, то и . Найдем область определения сложной функции f₃:

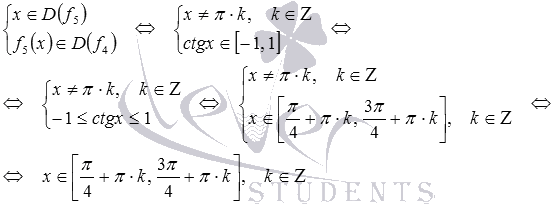
Теперь мы можем получить область определения исходной функции:

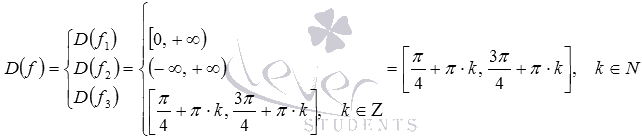
Ответ:

.

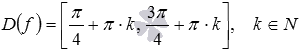Область определения произведения функций.

Если функция f - это произведение n функций (основных элементарных или элементарных) f₁, f₂, …, f_n, то есть, функция f задается формулой , то областью определения функции f является пересечение областей определения функций f₁, f₂, …, f_n. Итак, .

Пример.

Найдите область определения функции .

Решение.

Запишем заданную функцию в следующем виде , f₁ – это постоянная функция, f₂ – это функция арктангенс, а f₃ – логарифмическая функция с основанием e.

Нам известно, что и . Тогда

Ответ:

областью определения функции является множество всех действительных положительных чисел.

Отдельно остановимся на нахождении области определения функции, заданной формулой , где С – некоторое действительное число. Легко показать, что область определения этой функции совпадает с областью определения функции f. Действительно, функция – это произведение постоянной функции и функции f. Областью определения постоянной функции является множество всех действительных чисел, а область определения функции f есть . Тогда область определения функции есть 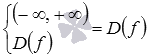, что и требовалось показать.

Итак, области определения функций y=f(x) и , где С – некоторое действительное число, совпадают.

В частности, области определения функций y=f(x) и y=-f(x) совпадают и можно утверждать, что область определения разности функций находится так же, как и область определения суммы n функций.

Пример.

Найдите область определения функции .

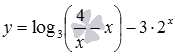Решение.

Данную функцию f будем рассматривать как разность двух функци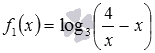й и . Тогда .

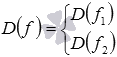Сначала найдем область определения функции f₁.

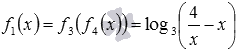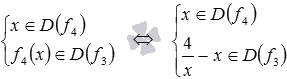
Эта функция сложная, ее можно представить в виде , где f₃ – логарифмическая функция с основанием 3, а . Тогда область определения сложной функции f₁ найдем, решив систему неравенств вида . Определив и , вернемся к этой системе.

Мы знаем, что . Найдем .

Функция f₄ – это разность двух функций и f₆(x)=x. Область определения функции f₅ совпадает с областью определения степенной функции с показателем -1, то есть, , а областью определения степенной функции с показателем 1 является множество всех действительных числе, то есть, . Так как область определения разности функций есть пересечение их областей определения, то .

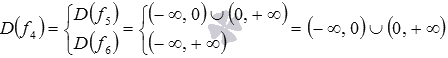Продолжим нахождение области определения функции f₁ и подставим полученные и в систему . Имеем

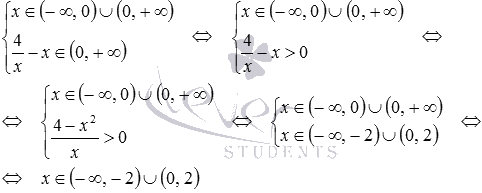
Таким образом, .

Теперь найдем область определения функции f₂.

Область определения этой функции совпадает с областью определения показательной функции с основанием 2, то есть, .

Наконец мы можем найти область определения исходной функции: .

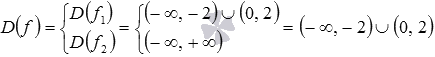Ответ:

.

Озвучим и докажем еще одно очень важное утверждение: область определения целой рациональной функции – это множество всех действительных чисел.

Рассмотрим целую рациональную функцию , где n – некоторое натуральное число, а - некоторые действительные числа. Она представляет собой сумму (n+1)-ой функции. Очевидно, что область определения каждой из функций – это множество всех действительных чисел, следовательно, областью определения исходной целой рациональной функции также является множество всех действительных чисел.

Пример.

Какова область определения функции ?

Решение.

Исходная функция (обозначим ее f) - это разность двух функций и . Функция f₁ – это целая рациональная функция, областью ее определения является множество всех действительных чисел. Область определения функции f₂ совпадает с областью определения степенной функции с показателем –ln5, то есть, .

Тогда .

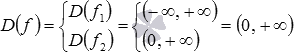Ответ:

.

К началу страницы