Нахождение области определения сложной функции.

Рассмотрим для начала сложную функцию f, которой соответствует формула . Какова же область определения сложной функции f ? Это множество всех x из области определения функции f₂, для которых f₂(x) входит в область определения функции f₁.

Таким образом, область определения сложной функции - это пересечение двух множеств: множества всех таких x, что , и множества всех таких x, для которых . То есть, областью определения сложной функции f является множество всех x, удовлетворяющих условию .

Записанная система представляет собой систему неравенств, решением которой является искомая область определения сложной функции .

Таким образом, нахождение областей определения сложных функций сводится к решению систем неравенств различного вида.

Давайте рассмотрим решения нескольких примеров, в которых находятся области определения сложных функций. Мы не будем подробно описывать решения систем неравенств, так как это выходит за рамки этой статьи.

Пример.

Найдите область определения сложной функции .

Решение.

Исходную сложную функцию можно записать в виде , то есть, f₁ – логарифмическая функция с основанием e, а f₂ – степенная функция с показателем 2.

Обратившись к известным областям определения основных элементарных функций, имеем и .

Тогда

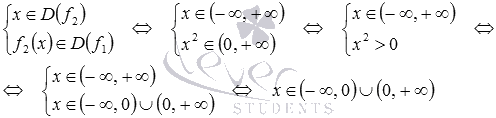
Следовательно, областью определения заданной сложной функции является множество всех действительных чисел, кроме нуля.

Ответ:

.

Пример.

Какова область определения функции ?

Решение.

Перепишем данную функцию в виде . Теперь стало видно, что нам требуется найти область определения сложной функции f=f₁(f₂), где f₁ – степенная функция с показателем , а f₂ – функция арксинус.

Нам известны области определения основных элементарных функций, откуда мы и заключаем, что и .

Осталось решить систему неравенств: .

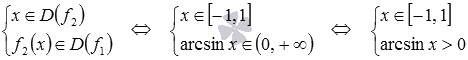Для решения неравенства вспомним свойства функции арксинус. Арксинус возрастает на всей области определения и обращается в ноль при x=0, следовательно, .

Вернемся к системе неравенств: .

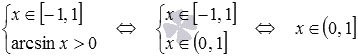Таким образом, областью определения исходной сложной функции является интервал .

Ответ:

.

Теперь давайте рассмотрим сложную функцию вида . Область определения функции f находится как решение системы вида

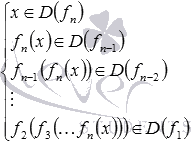
Пример.

Найдите область определения сложной функции .

Решение.

Заданную сложную функцию можно представить в виде , где f₁ – функция синус, f₂ – функция корень четвертой степени, f₃ – логарифмическая функция с основанием 10.

Нам известно, что .

Тогда область определения сложной функции f найдем, решив систему неравенств:

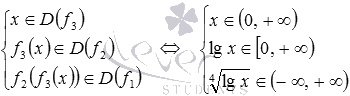
Условие равносильно условию , следовательно,

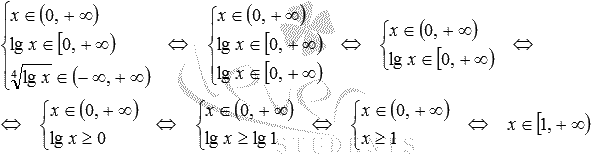
Ответ:

.

Замечание. В разобранных выше примерах мы специально брали сложные функции, составленные только из основных элементарных функций, чтобы лучше донести принцип нахождения области определения сложных функций. В следующих пунктах этой статьи мы разберем примеры нахождения областей определения сложных функций, составленных не только из основных элементарных функций, но и из элементарных функций.

К началу страницы