Область определения логарифмической функции.

Логарифмическая функция с основанием a, - это функция, заданная формулой . Логарифмическая функция с основанием a обозначается как , с основанием e – как , а с основанием 10 – как . Область определения логарифмической функции – это множество всех положительных действительных чисел, то есть, .

Область определения логарифмической функции не зависит от значения основания логарифма.

Приведем пример.

Областью определения логарифмических функций 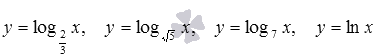является интервал .

К началу страницы

Область определения показательной функции.

Функция, заданная формулой y=f(x)=a^x, где , называется показательной функцией с основанием a, область определения показательной функции – это множество всех действительных чисел.

Область определения показательной функции не зависит от значения основания a.

Для примера приведем показательные функции 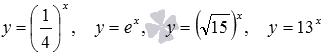, они определены на множестве .

К началу страницы

Области определения тригонометрических функций.

Функция, которую задает формула y=sinx, называется синусом и обозначается sin. Область определения синуса – это множество всех действительных чисел, то есть, .

Аналогично, функция, заданная формулой y=cosx, называется косинусом и обозначается cos. Область определения косинуса – множество всех действительных чисел: .

Функции, заданные формулами y=tgx и y=ctgx, называются тангенсом и котангенсом соответственно, и обозначаются tg и ctg. Область определения тангенса – это множество всех действительных чисел, кроме чисел . Область определения котангенса – это множество всех действительных чисел, кроме чисел .

Таким образом, если x – аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что и соответственно.

К началу страницы

Области определения обратных тригонометрических функций.

Функция, которая задается формулой y=arcsinx и рассматривается на сегменте , называется арксинусом и обозначается arcsin. Из этого определения понятно, что область определения арксинуса – это множество , то есть, .

Аналогично, функция, которая задается формулой y=arccosx и рассматривается на отрезке , называется арккосинусом и обозначается arccos. Таким образом, область определения арккосинуса есть отрезок , то есть, .

Функции, которые задаются формулами вида y=arctgx и y=arcctgx и рассматриваются на множестве всех действительных чисел, называются арктангенсом и арккотангенсом соответственно, обозначаются arctg и arcctg. Область определения арктангенса и область определения арккотангенса есть интервал , то есть, и .

Итак, теперь мы знакомы с областями определений всех основных элементарных функций и можем переходить к знакомству с областями определений элементарных функций.

К началу страницы

Нахождение области определения элементарных функций.

Мы выяснили, что функция задается вместе с ее областью определения. Тогда возникает логичный вопрос: «Зачем искать область определения функции, если она задается вместе с самой функцией»?

Действительно, области определения основных элементарных функций находить не надо, так как они заданы. Однако когда начинают рассматривать элементарные функции (определение элементарной функции дано в статье классификация элементарных функций), то области их определения уже часто не указывают. В этом случае подразумевают, что областью определения данной элементарной функции является множество X, на котором определены все функции, составляющие данную элементарную функцию. При этом множество X таково, что не существует никакого другого множества, на котором определена данная функция и которое содержит все элементы множества X. Вот так возникает задача поиска области определения элементарной функции.

Теперь встает новый вопрос: «Как найти область определения элементарной функции»?

Одной фразой на этот вопрос не ответишь, но смысл таков – области определения основных элементарных функций принимаются за основу, и, отталкиваясь от этих данных, находятся области определения элементарных функций.

Давайте будем постепенно разбираться с процессом нахождения областей определения элементарных функций различного вида.