2.2 Инверсная кинематика

Одной из задач поставленной в курсовом проектировании является написание кинематики движения робота. Решение данной задачи основано на рассмотрении биомеханики насекомых. Так как Hexapod не совсем паук, так как имеет шесть конечностей, то за основу его движений можно взять механику движения насекомых. Количество конечностей у них совпадает, а принцип движения основан на перемещении трех конечностей, пока опора установлена на 3 без движения (3 по 3).

Кинематика – это процесс вычисления позиции в пространстве для конца взаимосвязанной структуры при заданных углах поворота всех шарнирных точек. В робототехнике есть два подхода для решения задачи написания кинематики – это прямая и инверсная. Прямая кинематика, что передача параметров происходит по цепочке, от нижнего сегмента к верхнему. Это значит, что сначала свое положение изменит родительский сегмент, например, сервомотор, установленный на опоре, а затем всех зависимые от него сегменты. Данный тип кинематики чаще всего применяется при конструировании манипуляторов, и моделировании анимации. Инверсная кинематика построена по принципу, вычисления углов. Для начала создадим простой чертеж конечности (Рисунок 6 и Рисунок 7).

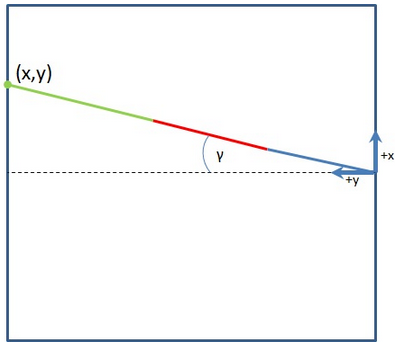
Рисунок 6. Вид сверху

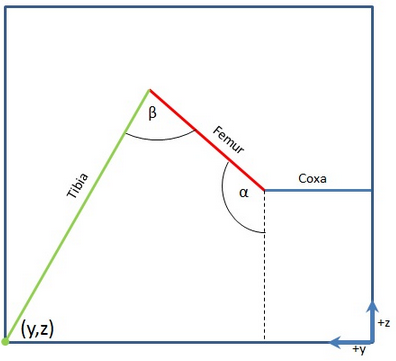
Рисунок 7. Вид с фронта

Вычисление угла гамма, этот угол обеспечивает движение робота вперед или назад:

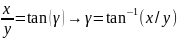
На следующем шаге следует вычислить угол альфа (α). Для простоты вычисления следует разделим угол на две части отрезком L.

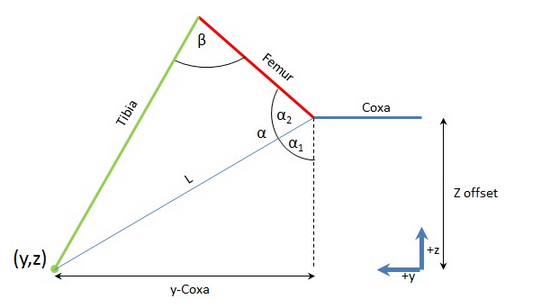
Рисунок 8. Расчет углов альфа и бета.

Вычислим α₁:

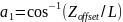
Вычисление α₂ является более сложной задачей, в качестве решения применяется закон косинусов:

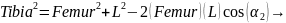
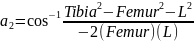
Угол α вычисляется как сумма двух углов:

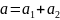
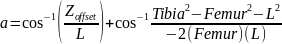
На последнем этапе произведем вычисление угла бета (β). Угол между Tibia и Femur. Данный угол отвечает за отрыв конечности от поверхности. Вычисление угла β производится аналогично углу альфа 2, по закону косинусов:

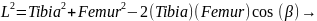
Данные формулы были перенесены в код на С++ для тестирования алгоритма инверсной кинематики. Кроме того, следует знать параметры конечности робота (tibia, femur, coxa):

#include "stdafx.h"

#include "iostream"

#include "math.h"

using namespace std;

int main()

{

double x ; //координата х, для следующего положения конечности

double y ; //координата y, для следующего положения конечности

cin >> x>>y; //ввод координат

//проверка области определения и области допустимых значений

if (abs(x)<=6)

{

cout << "error"<< endl;

system("pause");

return 0;

}

if(abs(x)>=19)

{

cout << "error"<< endl;

system("pause");

return 0;

}

if (abs(y)<=6)

{

cout << "error"<< endl;

system("pause");

return 0;

}

if(abs(y)>=19)

{

cout << "error"<< endl;

system("pause");

return 0;

}

const double z_offset = 4; //расстояние от поверхности

const double cox = 1; //длина Coxa

const double tibia = 13; //длина Tibia

const double femur = 6; //длина Femur

double L1,alfa,gamma,betta; //переменные для хранения углов

L1 = sqrt(pow(z_offset,2)+pow((y-cox),2));

alfa=(acos(z_offset/L1)+acos((pow(tibia,2)-pow(femur,2)-pow(L1,2))/((-2)*femur*L1)))*(180/3.14); //вычисление угла альфа

gamma = (atan2(x,y))*(180/3.14); //вычисление угла гамма

betta= (acos((pow(L1,2)-pow(tibia,2)-pow(femur,2))/((-2)*tibia*femur)))*(180/3.14); // вычисление угла бета

cout << "afemur: " << alfa<<endl; //вывод альфа

cout << "atebia "<< betta<<endl; //вывод бета

cout << "acoxa " << gamma <<endl; //вывод гамма

system("pause");

}