Определение ускорений точек в ппд

3.3.2. Мгновенный центр ускорений (мцу)

В учебной литературе доказывается, что при движении фигуры в плоскости в каждый момент времени существует такая точка плоской фигуры, ускорение которой в этот момент равно нолю. Эту точку называют мгновенным центром ускорений (МЦУ). В наших рассуждениях будем обозначать ее буквой Q. Взяв эту точку за полюс, получим формулу для определения ускорения произвольной точки:

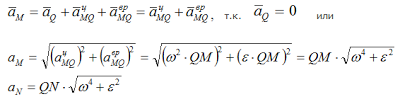
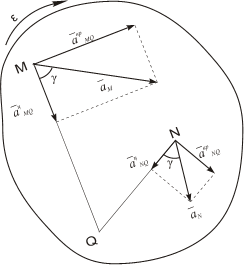
Рис. 1.12

Угол, который составляет вектор ускорения точки М с линией MQ определится из соотношения:

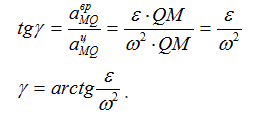
Т.е. у всех точек плоской фигуры этот угол одинаков. Из рис. 1.12 видно, что мгновенный    центр   ускорений   лежит    в точке  пересечения линий,  составляющих  угол γ с соответствующими ускорениями точек.

20

Тносительное, переносное и абсолютное движение точки

 

Сложным движением точки называется такое ее движение, при кото­ром она движется относительно системы отсчета, перемещающейся по отношению к некоторой другой системе отсчета, принятой за непод­вижную. Например, можно считать, что пассажир, идущий по вагону движущегося поезда, со­вершает сложное движение по отношению к полотну дороги, состоящее из движения пассажира по отношению к вагону (подвижная система отсчета) и дви­жения пассажира вместе с вагоном по отношению к полотну дороги (неподвижная система отсчета).

Движение точки по отношению к подвижной системе ко­ординат называется относительным движением точки. Скорость и ускорение этого движения называют относитель­ной скоростью иотносительным ускорением и обозначают    и  .

Движение точки, обусловленное движением подвижной системы координат, называется переносным движением точки.

Переносной скоростью и переносным ускорением точки на­зывают скорость и ускорение той, жестко связанной с под­вижной системой коор­динат точки, с которой совпадает в дан­ный момент времени движущаяся точка, и обозначают    и  .

Движение точки по отношению к неподвижной системе координат называ­ется абсолютнымили сложным. Скорость и ускорение точки в этом движении называют абсолютной скоростью иабсолютным ускорением и обозначают    и  .

В приведенном выше примере движение пассажира относительно вагона будет относительным, а скорость – относительной скоростью пассажира; движение вагона по отношению к полотну дороги будет для пассажира переносным движением, а скорость вагона, в котором находится пассажир, будет в этот момент его переносной скоростью; наконец, движение пассажира по отношению к полотну будет его абсолютным движением, а скорость – абсолютной скоростью.

21

Теорема о сложении скоростей

[править | править вики-текст]

Материал из Википедии — свободной энциклопедии

Теоре́ма о сложе́нии скоросте́й — одна из теорем кинематики, связывает между собой скорости материальной точки в различных системах отсчёта. Утверждает, что присложном движении материальной точки её абсолютная скорость равна сумме относительной и переносной скоростей^[1][2].

Содержание

  [показать] 

Сложное движение[править | править вики-текст]

Основная статья: Сложное движение

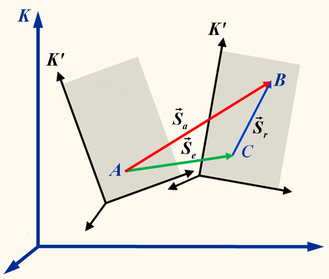
Сложное движение.

Движение в механике всегда рассматривается по отношению к какой-либо системе отсчёта. Однако в некоторых случаях бывает целесообразно или даже необходимо изучать движение материальной точки (МТ) относительно двух различных систем отсчёта одновременно. Одну из этих систем отсчёта условно считают неподвижной, базовой, а другую полагают движущейся относительно первой. Тогда движение точки можно рассматривать, как состоящее из двух движений: первое — движение относительно движущейся системы отсчёта, второе — движение вместе с движущейся системой относительно неподвижной. Такое движение точки называют сложным или составным.