Кинематика

1

Путь s — скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s > 0.

Перемещение Δr

⃗ тела за определенный промежуток времени — направленный отрезок прямой, соединяющий начальное (точка M0) и конечное (точка М) положение тела

Траектория — Годограф радиус-вектора, то есть — воображаемая линия, описываемая концом радиус-вектора в процессе движения. Иными словами, траектория — это линия вдоль которой движется материальная точка. При этом закон движения выступает как уравнение, задающее траекторию параметрически. Длину участка траектории между начальным и конечным моментами времени часто называют пройденным расстоянием, длиной пути или вульгарно — путем и обозначают буквой S. При таком описании движения S выступает в качестве обобщенной координаты, а законы движения в этом случае записывается в виде S = S(t) и аналогичны соответствующим законам для координат

2

Основная задача кинематики — это получение зависимостей от времени скорости v = v(t) и координат (или радиуса-вектора) r = r(t)материальной точки из известной зависимости от времени ее ускорения a = a(t) и известных начальных условий v0 и r0.

Существует и обратная задача: по известному закону движения r = r(t) находят скорость и ускорение материальной точки. Решение обеих задач в общем виде возможно с помощью дифференциального и интегрального исчисления

3

Естественный сп. указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t) – закон движения точки. При прямолинейном движении: х=f(t).

Координатный сп. положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f1(t), y=f2(t), z=f3(t).

Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде: f(x,y)=0 (для плоск-ти).

Векторный сп. положение точки определяется ее радиус-вектором , проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора. Связь между координатным и векторным способами: ,

( – орты – единичные вектора, сонаправленные с какой-либо осью)

модуль , направляющие косинусы: и т.д.

Переход от координатного способа к естественному: .

Скорость точки. Вектор ск-сти: – первая производная от радиус-вектора по времени (точка обозначает производную по времени); . Проекции скорости

4 досмотреть в интернете

Координатный способ задания движения точки

В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения:

x=x(t)

y=y(t) (1.4)

z=z(t)

Рисунок 1.3

Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей.

Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):

r(t)=i⋅x(t) ⊕ j⋅y(t) ⊕ k⋅z(t) (1.5)

Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:

То есть:

Направление вектора скорости определяется с помощью направляющих косинусов:

Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.

Аналогичны формулы для определения ускорения точки:

Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.

5

Смотри на ютюбе или в книге

6

Смотри на ютюбе или в книге

7

Смотри на ютюбе или в книге

8

Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.

Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли (рисунок 1.1) и т.д. 

Рис. 1.1

Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.

Доказательство. 

Если выбрать две точки твердого тела А  и В  (рисунок 1.2), то радиусы-векторы этих точек связаны соотношением

Траектория точки А  – это кривая, которая задается функцией r_A(t), а  траектория точкиB – это кривая, которая задается функцией r_B(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы.

Продифференцируем по времени выражение

Получаем

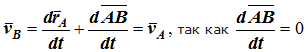
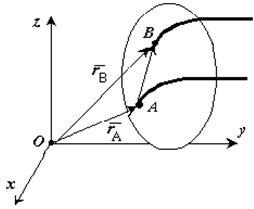
Рис. 1.2

Продифференцируем по времени скорость и получим выражение a_B = a_A. Следовательно, скорости и ускорения всех точек твердого тела одинаковы.

Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

9-10-11

Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П₀ и П , одна из которых неподвижна, а другая жестко связана с телом.

 φ=φ(t) – уравнение вращательного движения твердого тела.

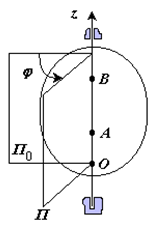
Рис. 1.3

За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z. Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.

Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:

В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту.  За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин).  Разделив этот угол на число секунд в минуте, получим

Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости

где k – единичный вектор оси вращения.

Угловое ускорение – мера изменения угловой скорости:

Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)

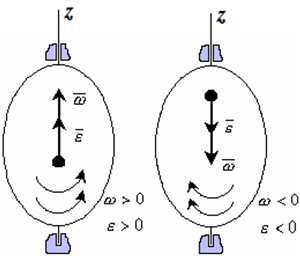
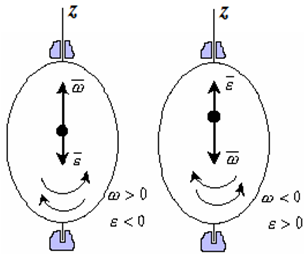
Рис. 1.4

Если ε >0 и ω >0 (рисунок 1.4), то угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону.  Направление векторов ω и ε совпадают, оба они направлены в положительную сторону оси вращения Oz.

При ε <0 и ω <0 – тело вращается ускоренно  в отрицательную сторону.  Направление векторов ω и ε совпадают, оба они направлены в отрицательную сторону оси вращения Oz .

Если ε <0 и ω >0, то имеем замедленное вращение в положительную сторону. Векторыω и ε направлены в противоположные стороны.

Если ε >0 при ω <0, то имеем замедленное вращение в отрицательную сторону. Векторыω и ε направлены в противоположные стороны.

Если угловая скорость  ω=const, то вращательное движение называется равномерным. Уравнение равномерного вращения

φ=φ₀+ωt

Если угловое ускорение ε=const, то вращательное движение называется равнопеременным. 

Уравнение равнопеременного вращения

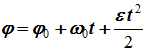
и уравнение, выражающее угловую скорость в любой момент времени

 ω=ω₀+εt

представляют совокупность основных формул вращательного равнопеременного движения тела.

12

Установив в предыдущих параграфах характеристики движения всего тела в делом, перейдем к изучению движения отдельных его точек.

1. Скорости точек тела. Рассмотрим какую-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения (см. рис. 134).

При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время   происходит элементарный поворот тела на угол   то точка М при этом совершает вдоль своей траектории элементарное перемещение   Тогда числовое значение скорости точки будет равно отношению   т. е.

или

Скорость v в отличие от угловой скорости тела называют иногда еще линейной или окруокной скоростью точки М.

Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения.

Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М.

Так как для всех точек тела со имеет в данный момент времени одно и то же значение, то из формулы (44) следует, что скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения. Поле скоростей точек вращающегося твердого тела имеет вид, показанный на рис. 136.

Рис. 136

Рис. 137

2. Ускорения точек тела. Для нахождения ускорения точки М воспользуемся формулами 

В нашем случае  . Подставляя значение v из равенства (44) в выражения   получим:

или окончательно:

Касательная составляющая ускорения   направлена по касательной к траектории (в сторону движения при ускоренном вращении тела и в обратную сторону при замедленном); нормальная составляющая   всегда направлена по радиусу МС к оси вращения (рис. 137).

Полное ускорение точки М будет   или

Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом   который вычисляется по формуле   [вторая из формул (22)]. Подставляя сюда значения   из равенств (45), получаем

Так как   имеют в данный момент времени для всех точек тела одно и то же значение, то из формул (46) и (47) следует, что ускорения всех точек вращающегося твердого тела пропорциональны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол  , с радиусами описываемых ими окружностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис. 138.

Рис. 138

Рис. 139

Формулы (44) — (47) позволяют определить скорость и ускорение любой точки тела, если известен закон вращения тела и расстояние данной точки от оси вращения. По этим же формулам можно, зная движение одной точки тела, найти движение любой другой его точки, а также характеристики движения всего тела в целом.

3. Векторы скорости и ускорения точек тела. Чтобы найти выражения непосредственно для векторов v и а, проведем из произвольной точки О оси АВ радиус-вектор   точки М (рис. 139). Тогда   а и по формуле (44)

Таким образом, - модуль векторного произведения   равен модулю скорости точки М. Направления векторов   тоже совпадают (оба они перпендикулярны плоскости ОМВ) и размерности их одинаковы. Следовательно,

т. е. вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки.

Формулу (48) называют формулой Эйлера.

Беря от обеих частей равенства (48) производные по времени, получим

или

Формула (49) определяет вектор ускорения любой точки вращающегося тела.

Вектор   направлен, как и вектор  , т. е. по касательной к траектории точки   Вектор же   направлен вдоль МС, т. е. по нормали к траектории точки М, а   так как   Учитывая все эти результаты, а также формулы (45), заключаем, что 

Задача 54. Вал, делающий   об/мин, после выключения двигателя начинает вращаться равнозамедленно и останавливается через   с. Определить, сколько оборотов сделал вал за это 

Решение. Так как вал вращается равиозамедленно, то для него, считая   будет

Начальной угловой скоростью при замедленном вращении является та, которую вал имел до выключения двигателя. Следовательно,

В момент остановки при   угловая скорость вала.   Подставляя эти вначения во второе из уравнений (а), получаем:

Если обозначить число сделанных валом за время   оборотов через N (не смешивать с n;   — угловая скорость), то угол поворота за то же время будет равен   Подставляя найденные значения   в первое из уравнений (а), получим

откуда

Задача 55. Маховик радиусом   пращаегся равномерно, делая   об/мин. Определить скорость и ускорение точки, лежащей на ободе маховика.

Решение. Скорость точки обода   где угловая скорость w должна быть выражена в радианах в секунду. Тогда 

Далее, так как   то   и, следовательно,

Ускорение точки направлено в данном случае к оси вращения.

Задача 56. Полагая, что при разгоне маховик вращается по закону

определить значения постоянных коэффициентов   и k из условий, что при   должно быть   и что предельная угловая скорость, до которой разгоняется маховик   а его угловое ускорение при разгоне не должно превышать значения 

Найти также, какое ускорение будет при этом у точек обода маховика в момент времени  , если радиус маховика 

Решение. Из уравнения (а) видно, что при   если 

Далее из уравнения (а) находим, что   Следовательно, при   если 

При этих значениях   уравнение (а) примет вид

Отсюда находим

Первое из равенств (в) показывает, что   со временем растет и при   стремится к предельному значению  следовательно,   Из второго же равенства видно, что   со временем убывает, стремясь к нулю, а наибольшее   чение   имеет при   следовательно, 

Но по условиям задачи   Тогда должно быть   откуда   При этих значениях k и   равенство   (б) дает окончательно следующий закон вращения маховика:

Тогда, что видно и из равенств (в), будет

 момента времени 1 с, учитывая, что   получим   Следовательно, в этот момент времени 

Задача 57. Груз В (рис. 140) приводит во вращение вал радиусом   и сидящую на одной оси с валом шестерню   ральуссч   Движение груза начинается из состояния покоя и происходит с постоянным ускорением а. Определить, по какому закону будет при этом вращаться находящаяся в зацеплении с шестерней   шестерня 2 радиуса  .

Рис. 140

Решение. Так как груз В начинает двигаться без начальной скорости, то его скорость в любой момент времени t равна   Эту скорость будут иметь и точки обода вала. Но, с другой стороны, скорости этих точек равны   где   общая для вала и шестерни 1 угловая скорость. Следовательно,

Теперь найдем   Так как скорость точки сцепления С должна быть одной и той же для обеих шестерен, то   откуда

Итак, угловая скорость шестерни 2 растет пропорционально времени. Учитывая, что   где   — угол поворота шестерни 2, получим

Отсюда, беря от обеих частей интегралы и считая, что при   угол   найдем окончательно закон равноускоренного вращения шестерни 2 в виде

13

 Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости (рисунок 2.11). 

    При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например M₁M₂ ) совершают одинаковые движения.

                                    

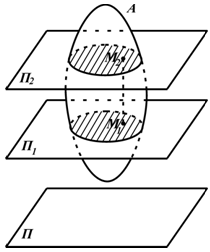
Рисунок 2.11

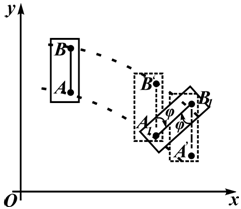
Рисунок 2.12

    Отрезок M₁M₂  движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости.

    На рисунке 2.12 показано перемещение пластинки в плоской системе отсчета xOy  из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A  с последующим поворотом на угол φ  вокруг точки A₁. Это же перемещение можно выполнить иначе. 

    Например, перемещая пластинку поступательно с траекторией точки B , с последующим поворотом вокруг B₁  на угол φ. Траектории точек A  и B различны, а угол поворота в обоих случаях  одинаков. 

     Положение пластинки вполне определяется положением скрепленного с ней отрезка (например AB), закон движения которого можно задать в виде:

                                 x_A=x_A(t),  y_A=y_A(t),  φ=φ(t).

    Точка A  в этом случае называется полюсом. Если принять за полюс точку B , то получим уравнения:

                                x_B=xB(t),  y_B=yB(t),  φ=φ(t)

    За полюс выбирается точка, закон движения которой известен.

14

Плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой фиксированной плоскости П (рис. 141). Плоское движение совершают многие части механизмов и машин, например катящееся колесо на прямолинейном участке пути, шатун в кривошипно-ползунном механизме и др. Частным случаем плоскопараллельного движения является вращательное движение твердого тела вокруг неподвижной оси.

Рис. 141

Рис. 142

Рассмотрим сечение S тела какой-нибудь плоскостью   параллельной плоскости П (рис. 141). При плоскопараллельном движении все точки тела, лежащие на прямой ММ, перпендикулярной сечению S, т. е. плоскости П, движутся тождественно.

Отсюда заключаем, что для изучения движения всего тела достаточно изучить, как движется в плоскости   сечение S этого тела или некоторая плоская фигура S. Поэтому в дальнейшем вместо плоского движения тела будем рассматривать движение плоской фигуры S в ее плоскости, т. е. в плоскости   При этом все результаты, которые будут получены в § 53—59 для точек плоской фигуры, справедливы, конечно, и для точек сечения S твердого тела, движущегося плоскопараллельно.

Положение фигуры S в плоскости   определяется положением какого-нибудь проведенного на этой фигуре отрезка АВ (рис. 142). В свою очередь положение отрезка АВ можно определить, зная координаты   точки А и угол   который отрезок АВ образует с осью   Точку А, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.

При движении фигуры величины   будут изменяться.

Чтобы знать закон движения, т. е. положение фигуры в плоскости   в любой момент времени, надо знать зависимости

Уравнения (50), определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела.

Первые два из уравнений (50) определяют то движение, которое фигура совершала бы при   это, очевидно, будет поступательное движение, при котором все точки фигуры движутся так же, как полюс А. Третье уравнение определяет движение, которое фигура совершала бы при   т. е. когда полюс А неподвижен; это будет вращение фигуры вокруг полюса А. Отсюда можно заключить, что в общем случае движение плоской фигуры в ее плоскости может рассматриваться как слагающееся из поступательного движения, при котором все точки фигуры движутся так же, как полюс А, и из вращательного движения вокруг этого полюса 

Рис. 143

Основными кинематическими характеристиками рассматриваемого движения являются скорость и ускорение поступательного движения, равные скорости и ускорению полюса   а также угловая скорость со и угловое ускорение   вращательного движения вокруг полюса. Значения этих характеристик в любой момент времени t можно найти, воспользовавшись уравнениями (50).

При изучении движения можно в качестве полюса выбирать любую точку фигуры. Рассмотрим, что получится, если вместо А выбрать в качестве полюса какую-нибудь другую точку С и определять положение фигуры отрезком CD, образующим с осью   угол   (рис. 143). Характеристики поступательной части движения при этом изменятся, так как в общем случае  (иначе движение фигуры было бы поступательным). Характеристики же вращательной части движения, т. е.  , остаются неизменными. В самом деле, проведя из С прямую   параллельную АВ, мы видим, что в любой момент времени угол  где   Отсюда   или 

Следовательно, вращательная часть движения от выбора полюса не зависит.

15

корость любой точки плоской фигуры равна геометрической сумме скорости выбранного полюса и скорости точки во вращательном движении фигуры вокруг полюса. 

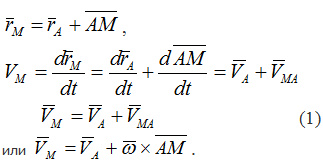
Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости  точки  М     при    вращении   ее вокруг точки А.

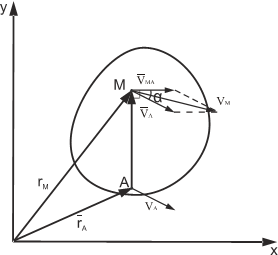
Рис. 1.3

Вектор V_MA= ω⋅AM перпендикулярен отрезку АМ.

Численную величину скорости точки М можно получить, если воспользоваться теоремой косинусов

или спроецировать векторное равенство (1) на выбранные оси координат

   

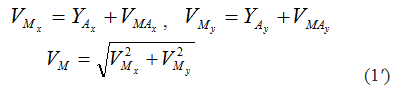
16

Определение скоростей точек плоской фигуры (или тела, движущегося плоскопараллельно) с помощью формулы (52) связано обычно с довольно сложными расчетами (см. задачу 59). Однако исходя из этого основного результата, можно получить ряд других, практически более удобных и простых методов определения скоростей точек фигуры (или тела).

Рис. 149

Один из таких методов дает теорема: проекции скоростей двух точен твердого тела на ось, проходящую через эти точки, равны друг другу.

Рассмотрим какие-нибудь две точки А и В плоской фигуры (или тела). Принимая точку А за полюс (рис. 149), получаем по формуле (52), что   Отсюда, проектируя обе части равенства на ось, направленную по АВ, и учитывая, что вектор  перпендикулярен А В, находим

и теорема доказана. Заметим, что этот результат ясен и из чисто физических соображений: если равенство (54) не будет выполняться, то при движении расстояние между точками А и В должно изменяться, что невозможно, так как тело считается абсолютно твердым. Поэтому равенство (54) выполиася не только при плоскопараллельном, но и при любом движении твердого тела.

Доказанная теорема позволяет легко находить скорость данной точки тела, если известны направление скорости этой точки и скорость какой-нибудь другой точки того же тела.

Задача 60. Найти зависимость между скоростями точек А и В линейки эллипсографа (см. рис. 145) при данном угле 

Решение. Направления скоростей точек А и В известны. Тогда, проектируя векторы   на ось, направленную по АВ, получим согласно доказанной теореме

17

Мгнове́нный центр скоросте́й — при плоскопараллельном движении абсолютно твёрдого тела точка, связанная с этим телом, которая обладает следующими свойствами: а) еёскорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело. Она существует в любой момент времени, но её положение меняется со временем за исключением одного случая — вращательного движения.

Содержание

  [показать] 

Положение мгновенного центра скоростей[править | править вики-текст]

Рис. 1. При качении колеса по горизонтальной дороге мгновенный центр скоростей находится в точке касания колеса и дороги — в точке А.  — полная скорость точки К;   — скорость точки Котносительно точки С, перпендикулярная прямой СК;   — параллельный перенос скорости точки С

Для того, чтобы определить положение мгновенного центра скоростей, необходимо знать направления скоростей любых двух различных точек тела, скорости которых не параллельны. Тогда для определения положения мгновенного центра скоростей необходимо провести перпендикуляры к прямым, параллельным линейным скоростям выбранных точек тела. В точке пересечения этих перпендикуляров и будет находиться мгновенный центр скоростей.

В том случае, если векторы линейных скоростей^[1] двух различных точек тела параллельны друг другу, и отрезок, соединяющий эти точки, не перпендикулярен векторам этих скоростей, то перпендикуляры к этим векторам также параллельны. В этом случае говорят, что мгновенный центр скоростей находится в бесконечности, и тело движется мгновенно поступательно.

Если известны скорости двух точек, и эти скорости параллельны друг другу, и кроме того, указанные точки лежат на прямой, перпендикулярной скоростям, то положение мгновенного центра скоростей определяется так, как показано на рис. 2.

Положение мгновенного центра скоростей в общем случае не совпадает с положением мгновенного центра ускорений. Однако в некоторых случаях, например, при чисто вращательном движении, положения этих двух точек могут совпадать.

18

Определение ускорений точек плоской фигуры

Покажем, что ускорение любой точки М плоской фигуры (так же, как и скорость) складывается из ускорений, которые точка получает при поступательном и вращательном движениях этой фигуры. Положение точки М по отношению к осям   (см. рис. 146) определяется радиусом-вектором   где   Тогда

В правой части этого равенства первое слагаемое есть ускорение   полюса А, а второе слагаемое определяет ускорение  которое точка М получает при вращении фигуры вокруг полюса А (см. § 54). Следовательно,

Значение   как ускорения точки вращающегося твердого тела, определяется по формулам (46) и (47) из § 51:

где   — угловая скорость и угловое ускорение фигуры, а   — угол между вектором   и отрезком МА (рис. 163).

Таким образом, ускорение любой точки М плоской фигуры геометрически складывается из ускорения какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка М получает при вращении фигуры вокруг этого полюса. Модуль и направление ускорения   находятся построением соответствующего параллелограмма (рис. 163).

Однако вычисление   с помощью параллелограмма, изображенного на рис. 163, усложняет расчет, так как предварительно надо будет находить значение угла   а затем — угла между векторами   Поэтому при решении задач удобнее вектор  заменять его касательной   и нормальной   составляющими и представить равенство (59) в виде

При этом вектор   направлен перпендикулярно АМ в сторону вращения, если оно ускоренное, и против вращения, если оно замедленное; вектор апмд всегда направлен от точки М к полюсу А (рис. 164). Численно же

Если полюс А движется не прямолинейно, то его ускорение можно тоже представить как сумму касательной   и нормальной   составляющих, тогда

Наконец, когда точка М движется криволинейно и ее траектория известна, то   в левых частях равенств (61) и (63) можно заменить суммой   Формулами (61) — (63) и пользуются обычно при решении задач.

Рис. 163

Рис. 164

Решение задач. Ускорение любой точки плоской фигуры в данный момент времени можно найти, если известны: 1) векторы скорости   и ускорения   какой-нибудь точки А этой фигуры в данный момент, 2) траектория какой-нибудь другой точки В фигуры. В ряде случаев вместо траектории второй точки фигуры достаточно знать положение мгновенного центра скоростей.

Тело (или механизм) при решении задач надо изображать в том положении, для которого требуется определить ускорение соответствующей точки. Расчет начинается с определения по данным задачи скорости и ускорения точки, принимаемой за полюс. Дальнейшие особенности расчета подробно рассматриваются в решенных ниже задачах. Там же даются необходимые дополнительные указания.

19