2.4 Регулярные языки и конечные автоматы

Ранее мы знакомились с понятием регулярных (автоматных) грамматик (языков). Напомним, что регулярная (автоматная) грамматика (тип 3) имеет правила (р) вида либо , где ; . При этом являются одиночными символами (не цепочками) соответствующих словарей (нетерминального и терминального). Язык, порожденный такой грамматикой, называется регулярным (автоматным).

Рассмотрим регулярный язык подробнее.

При описании автомата задается входной алфавит. Множество слов во входном алфавите называется событием. Этот термин стал традиционным в теории автоматов, хотя и не обязателен: можно обойтись термином просто «множество слов». Другой термин для множества слов - язык (множество всевозможных цепочек в некотором словаре).

Событие (язык) называется распознаваемым данным конечным автоматом, если оно в этом автомате представимо, т.е. если на вход автомата поступает это событие, то автомат достигает одного из своих заключительных состояний. Среди множества слов в событии может содержаться и пустое слово (цепочка) - слово нулевой длины. Пустое слово будем обозначать . Пустое слово не следует путать с пустым событием (т.е. с пустым множеством).

Автомат представляет пустое событие, если ни одно из его заключительных состояний не достижимо из начального состояния. Так как событие - это множество, то все операции под множествами справедливы для событий.

Вводим еще три операции над событиями. Пусть даны события и в алфавите . Для этих событий справедливы операции:

1. Объединение 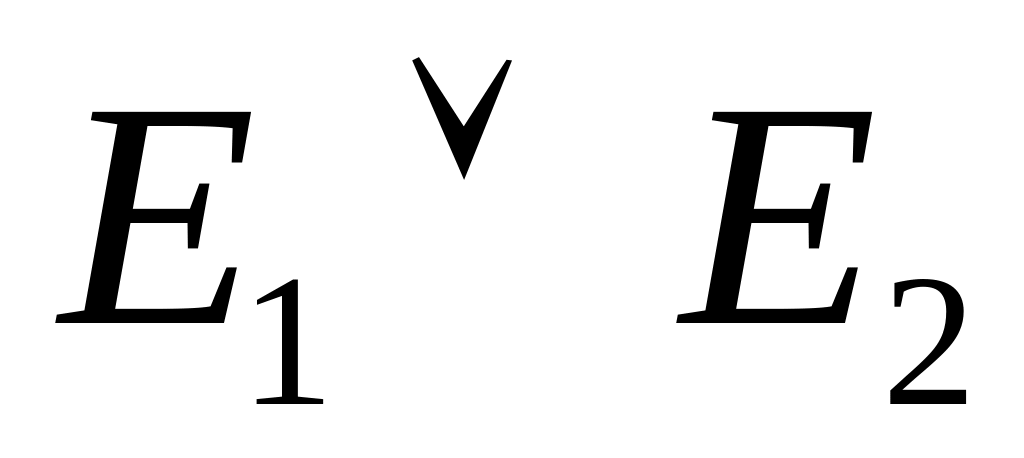(дизъюнкция), обозначается иногда 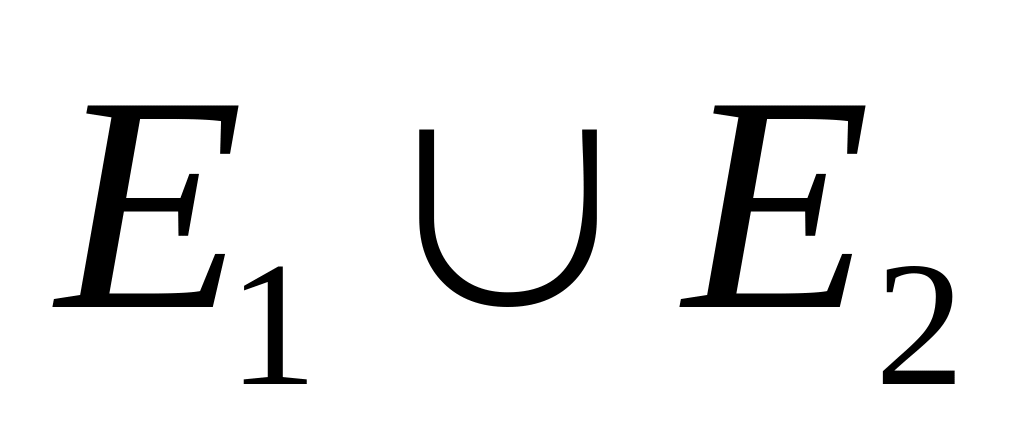- обычное объединение множеств.

2. Умножение (конкатенация - приписывание) 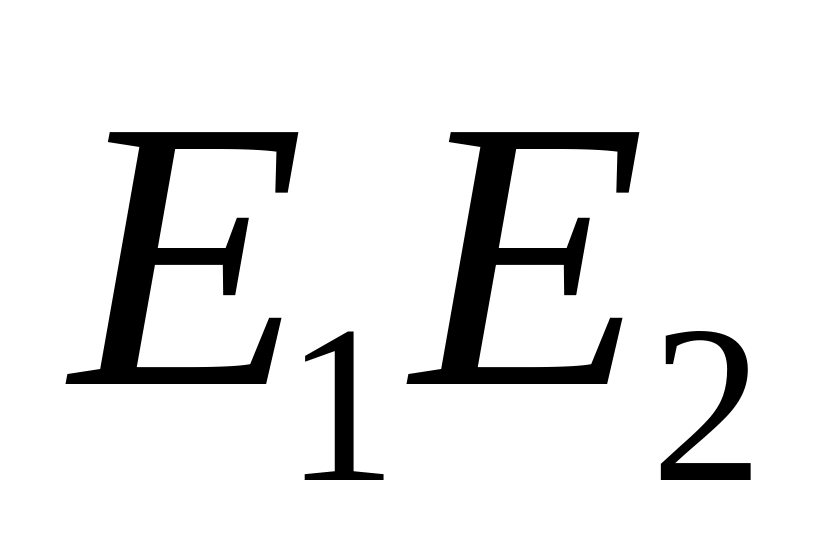; 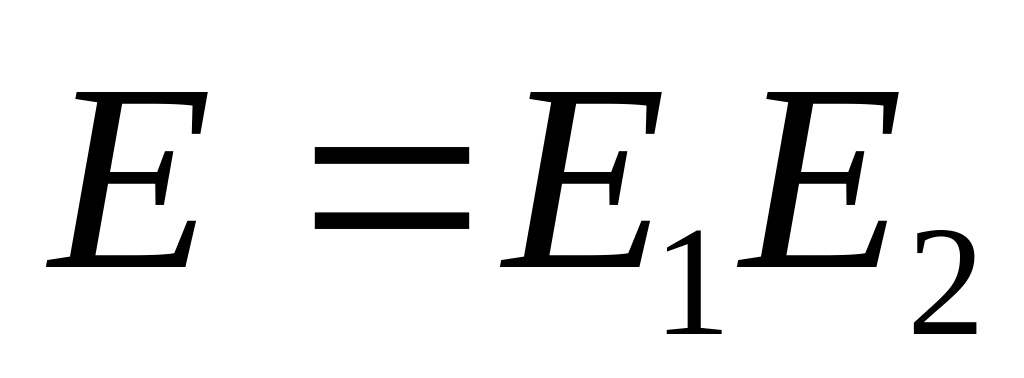- это множество всех слов вида 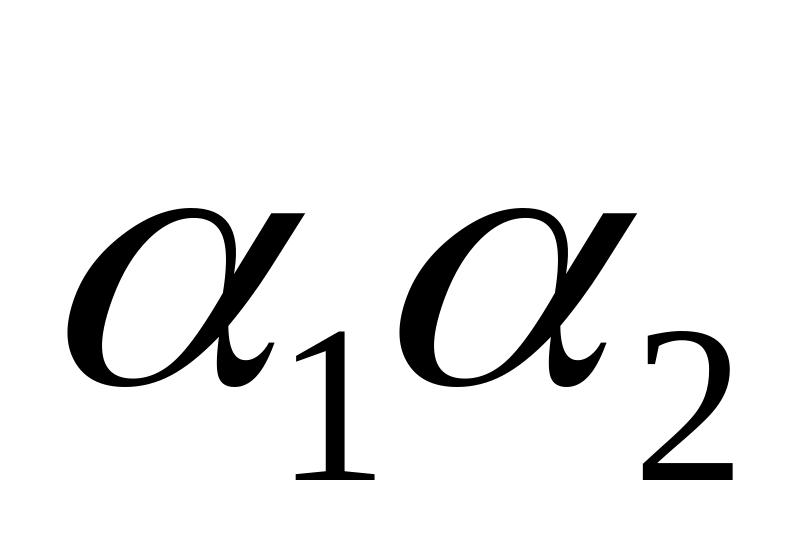, где 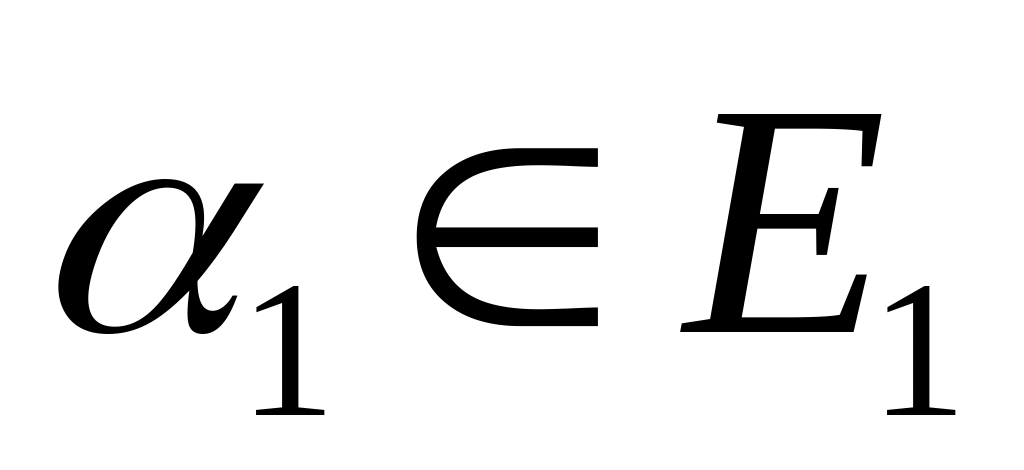, 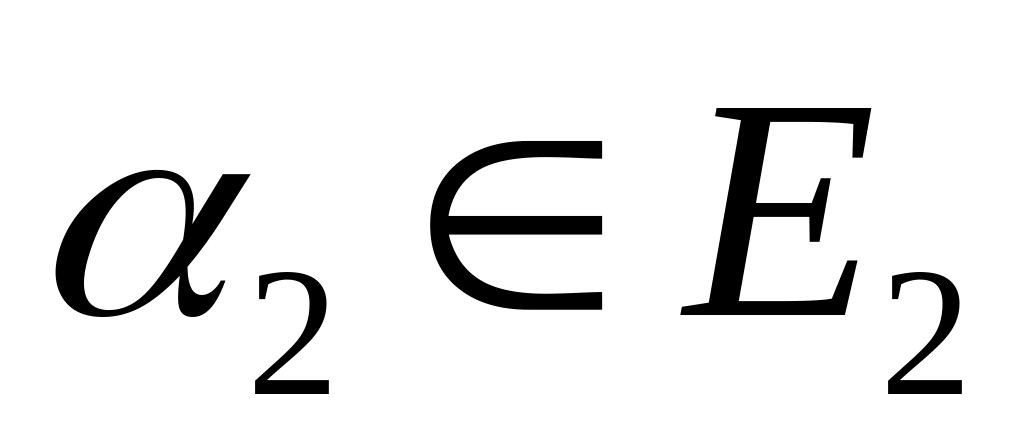- слово 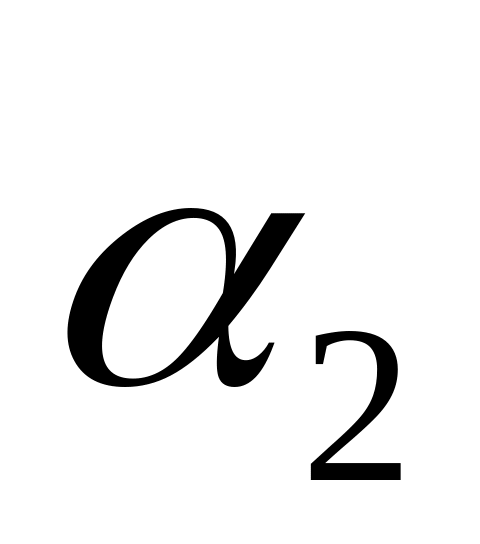приписывается справа к слову .

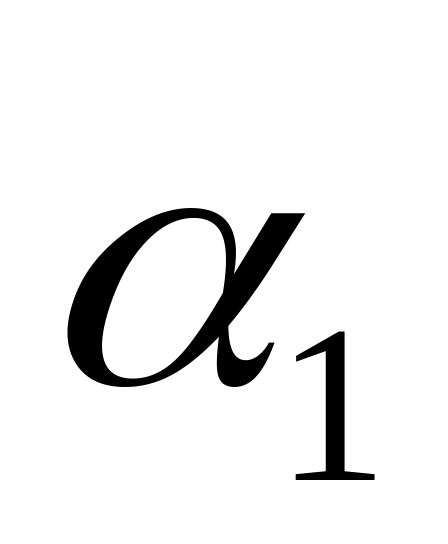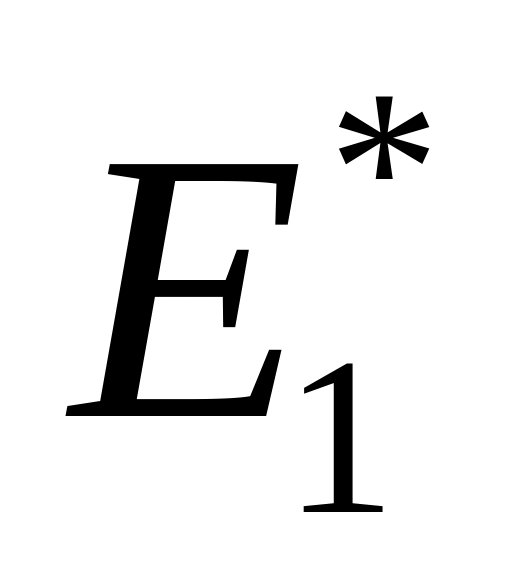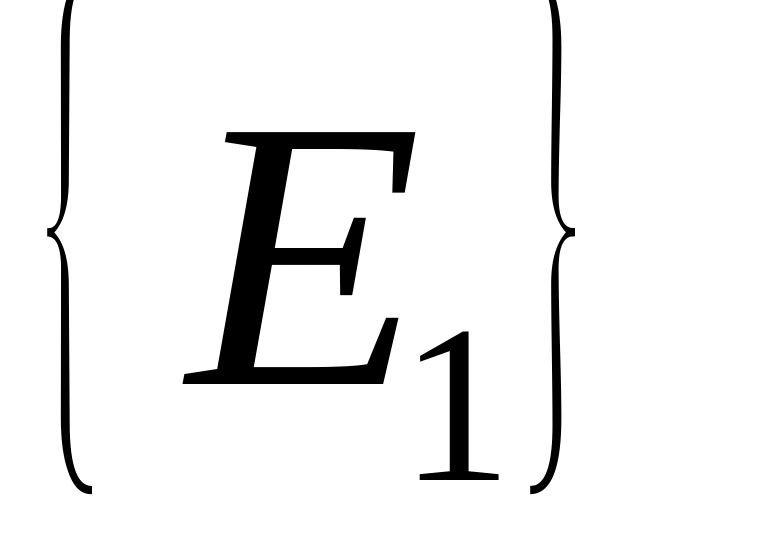3. Итерация (обозначается или , или )

( и так далее).

Итерация - это операция, применяемая к множествам слов некоторого алфавита , т.е. к событиям. Если - некоторое событие в алфавите , то будет событием, содержащим пустое слово и все те слова, которые можно составить из слов события , приписывая их друг другу в произвольном порядке. Например, если , то

Пусть алфавит , над которым рассматриваются события, состоит из букв (символов) . Тогда событие, состоящее из одного однобуквенного слова , будем называть элементарным и обозначать просто , (событие , где ). К элементарным отнесем также событие .

Событие называется регулярным, если оно может быть построено на элементарных событиях с помощью конечного числа применений операций объединения, умножения и итерации. Эти операции также назовем регулярными.

Таким образом, регулярное событие может быть описано формулой, содержащей символы образующих ( и буквы алфавита ) и знаки регулярных операций над ними. Такие формулы называются регулярными выражениями. Регулярные выражения эквивалентны, если они описывают одно и то же событие. Например, эквивалентные выражения - регулярные события, тогда:

; ;

; ; .

Операция объединения ассоциативна и коммутативна.

Отметим: множество, состоящее из одного слова является регулярным событием, поскольку любое выражение вида регулярно: оно построено из букв с помощью конкатенации.

Любое конечное множество слов регулярно и описывается выражением , не содержащим итерации.

Если регулярное выражение не содержит итерации, то раскрытие скобок преобразует его к виду , т.е. описывает конечное событие. Если же содержит итерацию, то оно бесконечно, за исключением случаев, когда итерация применяется только к ( , т.е. конечно).

Регулярное выражение вида , где - конечное событие, не содержащее пустого слова, описывает бесконечное событие, содержащее все слова из , кончающиеся словами на . Например:

1) событие содержит все слова в алфавите , кончающиеся на или (бесконечно);

2) событие содержит все слова в алфавите , начинающиеся и кончающиеся или (бесконечно).

Событие состоит из всех слов в алфавите , содержащих ровно два раза.

Событие состоит из всех слов, содержащих четное число раз.

Регулярные события и только они представимы в конечных автоматах.

Конечный автомат можно рассматривать как устройство, распознающее некоторое множество входных слов. Поступление на вход автомата последней буквы такого слова вызывает (в тот же момент) особую внешнюю реакцию автомата, т.е. некоторое подмножество выходных символов.

Множество всех цепочек (слов), воспринимаемых автоматом , образует язык , представимый данным автоматом. С другой стороны, множество слов во входном алфавите называют событием.

Таким образом, язык, представимый данным автоматом, есть событие.

Регулярное событие обозначает регулярный язык (или язык регулярных событий, или язык регулярных выражений).

Конечные автоматы представляют только регулярные языки. Итак, конечным автоматом (или просто автоматом) называется система , в которой , , - конечные множества (алфавиты) входов, состояний и выходов автомата соответственно, a и - функции, определенные на этих множествах (здесь «:» - функция отображения, « » - декартово перемножение множеств).

- входной алфавит, - выходной алфавит, - алфавит состояний, - функция переходов, - функция выходов.

Если, кроме того, в автомате выделено одно состояние, называемое начальным (обычно считается, что это ), то такой автомат называется инициальным и обозначается .

Функции и конечны и могут задаваться либо формулами, либо таблицами (таблицы переходов, таблицы выходов, таблицы переходов-выходов).

Отображение (функция, оператор) есть закон соответствия, сопоставляющий каждому элементу множества некоторый (единственный) элемент множества .

Обозначается - задано отображение в .

Декартовым (прямым) произведением множеств и называется множество всех пар вида , в которых первый компонент принадлежит множеству , а второй - множеству .

Конечный автомат может задаваться и графом переходов, тогда , где - входной алфавит автомата , совпадающий с терминальным алфавитом грамматики , - множество состояний, - начальное состояние, - конечное состояние, - граф переходов, определяющий функционирование автомата.

Каждому нетерминалу грамматики соответствует вершина графа , помеченная символом (состояния). В графе есть еще одна вершина, помеченная символом заключительного состояния . Единственному начальному состоянию автомата соответствует вершина, помеченная аксиомой . Далее для каждой незаключительной продукции проводится ребро, помеченное терминальным символом , из вершины в вершину ; для каждой заключительной продукции проводится ребро из вершины в вершину .

Автомат функционирует следующим образом: на вход последовательно (слева направо) подаются символы цепочки , . Движение по графу начинается с вершины , что соответствует начальному состоянию автомата , в котором он воспринимает символ . Затем осуществляется переход из вершины по любому из ребер , к некоторой вершине , после чего автомат воспринимает очередной символ и т.д. Если на некотором шаге осуществляется переход в вершину , у которой отсутствует ребро с пометкой, соответствующей очередному символу на входе, то автомат останавливается безрезультатно. В противном случае входная цепочка переведет автомат из начального состояния в некоторое состояние .

Путь в графе , соответствующий такому переходу, называется путем из вершины в вершину , несущим цепочку .

Цепочка воспринимается автоматом, если для нее в графе Г существует, по крайней мере, один путь из начальной вершины в заключительную вершину , несущий данную цепочку.

Множество всех цепочек, воспринимаемых автоматом , образует язык , представимый данным автоматом.

Очевидно, цепочка воспринимается автоматом тогда и только тогда, когда она выводима в соответствующей автоматной грамматике (языке) - так что .

Конечные автоматы представляют только регулярные языки (события).