2.3 Сети Петри

Автомат является математической абстракцией системы (машины, устройства) переработки информации или процесса переработки.

Автоматы, построенные из определенных компонентов по определенным правилам, часто представляются сетями, т.е. графами специального вида с дополнительной интерпретацией вершин и дуг.

Понятие конечного автомата существенно связано с понятием алгоритма и последовательной алгоритмической системы. Для них характерен последовательный способ функционирования: автомат (система) последовательно переходит из состояния в состояние в соответствии с заданной функцией перехода и осуществляет очередной (последовательный) шаг алгоритма.

По мере усложнения дискретных систем все большее внимание получают «неалгоритмические» параллельные системы с недетерминированным поведением, в которых отдельные компоненты, в основном, независимо взаимодействуют друг с другом время от времени (например, многопроцессорные вычислительные машины).

Термины классической теории автоматов не могут адекватно описать такие системы. Например, некоторое число пользователей вводит информацию в ЭВМ с разных терминалов, процессор ЭВМ занят трансляцией в машинный код, одновременно идет перепись файла с диска в буфер канала, связанного с печатающим устройством и т.п.

Среди многих существующих методов описания и анализа дискретных параллельных систем выделился подход, который основан на использовании сетевых моделей, восходящих к сетям специального вида. Метод предложен Карлом Петри (в 1962 г.) для моделирования асинхронных информационных потоков в системах преобразования данных - сети Петри.

Таким образом, к числу языков, которые могут быть использованы не только для задания алгоритма функционирования автомата, но и для его построения можно отнести язык сетей Петри.

Сеть Петри является двудольным графом, содержащим вершины двух типов - позиции и переходы - направленные ребра (дуги), которые могут соединять вершины разных типов (Рисунок 2.7).

Двудольным графом называется граф , если множество его вершин распадается на два непересекающихся подмножества и , таких, что каждое ребро графа G имеет один конец на , а другой - на . Двудольный граф может быть как неориентированным, так и ориентированным.

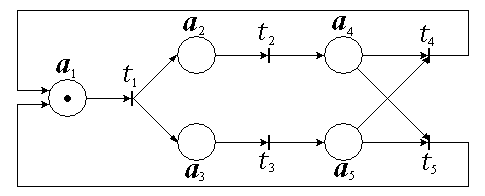
Рисунок 2.7 – Сеть Петри

Кружочками обозначены вершины, именуемые позициями ( ). Вертикальными линиями - вершины, называемые переходами ( ).

Множество позиций, которые соединены с определенным переходом направленными к нему ребрами, называют входными позициями данного перехода.

Все позиции, к которым направлены ребра от перехода, образуют множество выходных позиций этого перехода.

Каждой вершине графа, соответствующей позиции сети Петри, может быть поставлено в соответствие неотрицательное число меток, которые на рисунке обозначаются точками внутри кружка.

Начальное распределение меток соответствует начальным условиям работы сети и называется начальной маркировкой. Таким образом, сеть Петри может быть задана следующей четверкой: , где - конечное множество позиций; - конечное множество переходов. При этом , (т.е. и не пересекаются и не объединяются).

- это функция, определяющая связи между позициями и переходами так, что

определяет начальную маркировку сети и является К-мерным вектором неотрицательных чисел (К - число позиций), j-й элемент которого обозначает число меток в позиции .

Для сети Петри, приведенной на рисунке:

(количество позиций К и число переходов l),

- только имеет одну метку.

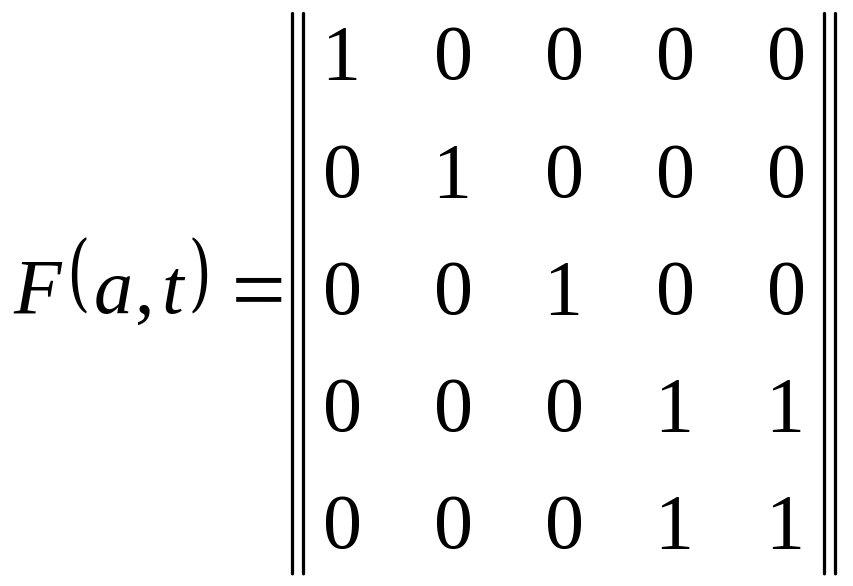
В матрице строки - это , столбцы - .

В матрице строки – это , столбцы - .

Если все входные позиции перехода , содержат метки, то такой переход является активным. Активный переход может быть реализован.

Иногда об активных переходах говорят как о воспламененных, а реализацию перехода называют его сгоранием.

В результате реализации (сгорания) перехода удаляется одна метка на каждой входной позиции и помещается по одной метке в каждую выходную позицию.

Таким образом, метка позиции может быть использована для реализации только одного перехода.

Реализацию перехода можно представить как событие, осуществляющееся при выполнении условий, в результате чего старые условия исчезают и соединяются в новые, при этом общее число меток в сети может измениться.

Существенно, что не все активные переходы должны быть реализованы, но допустима реализация только активных переходов.

Для нашего примера (Рисунок 2.7) в сети Петри начальная маркировка, в соответствии с которой имеется метка в позиции , делает активным переход . После реализации этого перехода метка в удаляется и метки помещаются в позиции и , что соответствует распараллеливанию процесса. Затем реализуются переходы и и появляются метки в и . Эти события могут происходить в разные моменты времени, т.к. относятся к различным параллельно протекающим процессам. Однако ни , ни не могут быть реализованы, пока оба эти процесса не закончатся. Затем реализуется какой-либо из переходов или , и сеть Петри переходит в начальное состояние.

Следует отметить, что многими авторами рассматривались различные типы сети Петри, для которых вводятся разные ограничения на заполнение позиций метками, на условия реализации переходов, на число входящих и исходящих дуг позиции.

Сеть Петри является удобным и наглядным средством описания взаимодействующих процессов. Протекание процесса соответствует последовательности реализации переходов, что вызывает перемещение меток по сети, т.е. изменение состояния процесса.

Кроме того, сеть Петри может быть использована для описания алгоритма функционирования дискретного устройства (автомата), управляющего некоторым объектом управления (ОУ). При этом требуется определенная интерпретация элементов сети Петри. Разными авторами предлагаются различные интерпретации, выбор которых зависит как от способа реализации синтезируемого автомата (аппаратурная, программная, микропрограммная реализация), так и от свойств ОУ.

При одной из возможных интерпретаций предполагается, что в результате реализации перехода происходит не только перемещение меток по сети, но и формируется сигнал (выходной сигнал), воздействующий на ОУ.

Такие сигналы могут рассматриваться как команды, которые должны быть выполнены в управляемой системе. После выполнения команды ОУ выдает сигнал, который ставит метку в соответствующую позицию сети Петри. Эти позиции называются внешними, в отличие от внутренних, которые получают метки в результате реализации переходов сети Петри. Внешние позиции могут получать метки не только от ОУ, но и от других устройств управления или от человека-оператора. Пример фрагмента такой сети Петри приведен на рисунке 2.8, где и - команды, которые должны выполняться в ОУ; , , - внешние позиции, которые получают метки извне и от ОУ.

Сеть Петри позволяет наглядно проследить протекание процесса, однако для построения устройства управления (автомата) реализуемый им алгоритм должен быть детерминированным.

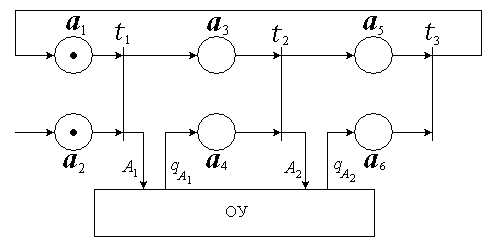
Рисунок 2.8 – Сеть Петри (фрагмент)