2.2 Магазинный автомат

Магазинный автомат - это автомат специального вида (как правило, бесконечный), в основе которого лежит понятие магазинной памяти или магазина. Автомат имеет специальную память типа «магазин».

Магазин удобно представлять в виде бесконечной в одну сторону ленты, состоящей из ячеек, пронумерованных числами 1,2,3,... . Лента расположена вертикально таким образом, что первая ячейка (ячейка с номером 1) оказывается самой верхней. В каждый момент времени в магазине записано некоторое слово. Первая его буква (символ) записана в первой ячейке, вторая - во второй и т.д., остальные ячейки магазина «пусты», т.е. записаны специальными «нулевыми» символами.

Магазин работает в двух режимах - чтения и записи. При чтении (за один такт) воспринимается лишь верхняя буква слова, записанного в магазине. Эта буква стирается, а оставшаяся часть слова поднимается на одну ячейку вверх. При записи в магазин слова длины m слово, записанное там, сдвинется на m ячеек вниз, а в освободившейся ячейке записываются символы слова (Рисунок 2.5).

Таким образом, чтение слова на магазине происходит в обратном порядке по сравнению с порядком его записи, т.е. символ, записанный в магазин последним, воспринимается при чтении как первый.

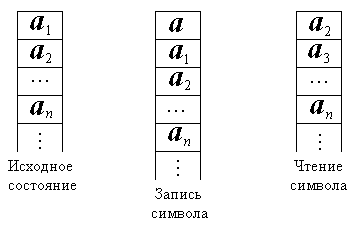
Рисунок 2.5 – Магазинная память

Вообще говоря, понятие ленты можно трактовать как абстрактную модель памяти бесконечных автоматов (память бесконечна).

В общем случае лента может быть эластичной. При этом номер ячейки играет роль адреса при обращении к ленте (к памяти). В каждый момент времени содержимым ленты является цепочка произвольной длины , которая располагается в n верхних ячейках, по одному символу в ячейке. Остальные ячейки остаются пустыми. В режиме записи по указанному адресу (номер ячейки) весь «хвост» цепочки сдвигается вниз, а в ячейку с указанным адресом записывается указанный символ.

В режиме чтения символ на ячейке с указанным адресом считывается, затем стирается, и «хвост» цепочки смещается на одну ячейку вверх.

При записи исходное слово удлиняется, при чтении - укорачивается. Это все для эластичной ленты.

Структура магазинного автомата представлена на рисунке 2.6. Он состоит из конечного управляющего автомата, снабженного тремя каналами для работы с магазинами - входным, выходным, внутренним.

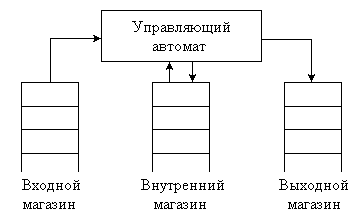
Рисунок 2.6 – Структура магазинного автомата

Входной магазин работает всегда в режиме чтения (задает входной алфавит), выходной - в режиме записи (выходной алфавит), а внутренний - в режиме и чтения, и записи (алфавит внутренних состояний).

Множество состояний управляющего автомата разбито на два непересекающихся подмножества и . Если состояние управляющего автомата относится к подмножеству , то происходит считывание из входного и внутреннего магазинов, если же оно относится к подмножеству то происходит считывание только из внутреннего магазина. В этот же момент автомат переходит в новое состояние и записывает во внутренний и выходной магазины некоторые слова.

Пусть , и - алфавиты входного, выходного и внутреннего магазинов, не включающие «пустой» буквы (символа), - множество внутренних состояний автомата.

Тогда магазинный автомат задается двумя функциями и .

Значение этих функций указывает новое состояние автомата и слова, которые записываются во внутренний и выходной магазины ( - в зависимости от состояния автомата ( ), входного ( ) и внутреннего ( ) магазинов, - в зависимости от состояния автомата ( ) и внутреннего магазина ( )).

Различают распознающие магазинные автоматы, или акцепторы (выходной алфавит пуст), порождающие магазинные автоматы (входной алфавит пуст), и магазинные преобразователи, или трансдьюсеры (общий случай).

Для определения способа функционирования магазинного автомата рассмотрим понятие конфигурации.

Конфигурацией называется четверка , где ; ; ; , где - цепочки из множества и т.д.

Конфигурация называется заключительной, если она имеет вид , где , -пустое слово.

Для распознающих автоматов в определении конфигурации следует отбросить четвертый компонент (выходной алфавит пуст), а для порождающих - первый (входной алфавит пуст).

В множестве выделяют также начальное состояние и множество заключительных состояний , а в множестве - начальный символ .

Распознающий магазинный автомат представляет (распознает) язык, состоящий из всех слов таких, что конфигурация переходит в одну из заключительных конфигураций . Порождающий магазинный автомат порождает язык, состоящий из всех слов таких, что конфигурация переходит в заключительную конфигурацию вида .

Магазинный автомат распознает (порождает) язык, относящийся к классу контекстно-свободных языков.