2 Автоматы – распознаватели языков

Напомним, что грамматики бывают порождающие и распознающие.

Концепция порождения заключается в том, что данной грамматикой порождается язык как множество цепочек в терминальном словаре этой грамматики, выводимых из ее начального символа.

Концепция распознавания заключается в том, что распознается, является ли заданная цепочка правильной в смысле данной грамматики (состоящей из ее терминальных символов), т.е. фактически - является ли заданный язык порожденным грамматикой .

Учитывая, что автомат - математическая модель устройства, предназначенного для преобразования последовательности (множества) входных дискретных сигналов в последовательность (множество) выходных дискретных сигналов, можно по заданному в том или ином виде автомату найти отображение «вход - выход», осуществляемое этим автоматом. Часто такое отображение можно интерпретировать как вычисление предиката. Напомним, что предикатом называется функция от любого числа аргументов, принимающая только два значения - истина (1) и ложь(0).

Аргументы принимают значения из произвольного конечного или бесконечного множества, необязательно двоичного.

Предикат характеризуется таблицей (множеством) истинности, которая показывает, на каких значениях аргументов предикат получит значение «истина». Поскольку каждый предикат полностью характеризуется своим множеством истинности, то задача анализа автомата сводится к нахождению этого множества.

Говорят, что множество распознается автоматом. Можно упрощенно сказать, что автомат распознает множество отображений «вход-выход», т.е. распознает языки.

Для многих классов автоматов хорошо известны классы распознаваемых ими множеств (языков). Например, машины Тьюринга распознают все рекурсивно перечислимые множества, автоматы с магазинной памятью (недетерминированные) - контекстно-свободные языки, конечные автоматы - регулярные языки (события).

Таким образом, автоматы распознают языки, т.е. являются распознавателями. Можно указать в качестве распознавателей автоматы: машина Тьюринга, магазинный автомат, сеть Петри, конечный автомат. Рассмотрим кратко эти автоматы.

2.1 Машина Тьюринга

Энциклопедия кибернетики определяет машину Тьюринга как математическое понятие, введенное как формальное уточнение понятия алгоритма.

А. Тьюринг - английский математик (1912 - 1954) ввел это понятие в 1936 г., т.е. машина Тьюринга разработана еще до создания ЭВМ.

Машина Тьюринга (Рисунок 2.1) является теоретической моделью алгоритмов (процессов вычисления), основанной на использовании конечного автомата специального вида.

Машина Тьюринга включает в себя три отдельные части:

1. Неограниченная в обе стороны лента, разделенная на ячейки.

2. Управляющее устройство (УУ) - конечный автомат, которое может находиться в одном из состояний, образующих конечное множество.

3. Считывающая и записывающая головка (Г) - устройство обращения к ленте, которая в каждый момент времени «обозревает» ячейку.

Каждая машина Тьюринга (МТ) характеризуется двумя конечными алфавитами: алфавит внешних символов , каждый из которых может быть записан в конкретной ячейке ленты, и алфавит внутренних состояний УУ . УУ может находиться в любом из состояний конечного множества . Обычно среди состояний управляющего устройства выделяется начальное и конечное (заключительное) состояние (k - мнемонический знак окончания работы). В начальном состоянии МТ находится перед началом работы, в конечном - машина останавливается после окончания работы. Иногда конечное состояние не назначается. Работа прекращается, когда на каком-то такте изменения конфигурации не происходит.

В любой момент времени в каждой ячейке ленты записан один символ из множества или пустой символ (пустая ячейка), обозначим его символом пробела (иногда в качестве пустого символа (пробела) включается в алфавит символ ), УУ находится в одном из состояний , Г обозревает одну из ячеек ленты.

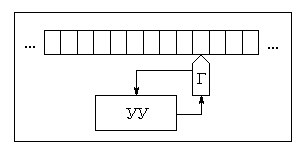
Рисунок 2.1 – Общая схема машины Тьюринга

Совокупность сведений о состоянии УУ и записи на ленте машины с указанием обозреваемой ячейки называется конфигурацией машины.

Работа машины Тьюринга состоит из тактов, в каждом из которых выполняется преобразование конфигурации, в которой МТ находится в данный момент времени , в конфигурацию, в которой машина будет находиться в момент . Это преобразование зависит только от состояния УУ и содержимого обозреваемой ячейки в момент и заключается:

а) в изменении состояния , в некоторое состояние ,

б) в замене символа , записанного в обозреваемой ячейке, некоторым символом (или пустым символом -пробелом);

в) в сдвиге Г на одну ячейку влево или вправо или отсутствии сдвига.

Такое преобразование называется командой машины Тьюринга. Символически команда записывается в виде , где - одна из букв Л, П, Н (Л означает сдвиг влево, П - сдвиг вправо, Н - отсутствие сдвига). Иногда пишут в латинском алфавите , и .

Совокупность всех команд, которые выполняет машина Тьюринга, называется ее программой.

Для каждого символа и состояния программа содержит в точности одну команду с левой частью . Поэтому работа МТ определяется однозначно, если фиксировать конфигурацию , с которой она начинает работу: в первом такте преобразуется в конфигурацию выполнением единственной применимой к команды, во 2-м такте таким же образом преобразуется в конфигурацию и т.д. Конфигурация, в которой машина останавливается, называется заключительной. Память машины Тьюринга - конечное множество состояний УУ (внутренняя память) и лента (внешняя память). Лента бесконечна в обе стороны, однако в начальный момент времени только конечное число ячеек ленты заполнено символами, остальные пусты, т.е. содержат пустой символ.

Данные машины Тьюринга - это слова в алфавите ленты, на ленте записываются исходные данные и затем - результат. Элементарные шаги - это считывание и запись символов, сдвиг головки, переход УУ из состояния в состояние.

Структурная схема универсальной машины Тьюринга представлена на рисунке 2.2.

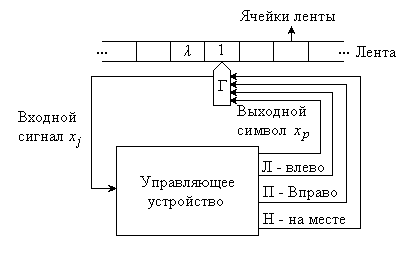
Рисунок 2.2 – Структурная схема машины Тьюринга

Под воздействием входного сигнала , например 1, считываемого головкой из ячейки, управляющее устройство формирует выходной символ и управляет движением головки - влево (л), вправо (п), на месте (н).

Таким образом, конечный автомат (УУ) управляет обработкой информации, реализует алгоритм. Тьюринг выдвинул тезис «всякий алгоритм может быть реализован машиной Тьюринга». Отсюда следует вывод - если невозможно построить машину Тьюринга для некоторых вычислений, значит, такой алгоритм отсутствует.

При построении универсальных машин (т.е. таких, на которых можно вычислять любую вычислимую функцию) исходят из того, что можно осуществить такое кодирование программ и конфигураций машины Тьюринга словами в фиксированном алфавите, например в алфавите , что по коду программы П легко восстановить любую команду из П и по коду конфигурации К-ю команду, которая применима к К.

Аналогия между универсальными машинами Тьюринга и универсальными ЭВМ заключается в том, что те и другие снабжаются, кроме исходных данных решаемой задачи, программой ее решения.

По существу, универсальную МТ можно считать идеализированной моделью универсальной ЭВМ. При этом отвлекаются от того обстоятельства, что ЭВМ обладает конечной памятью, поскольку ее внешнюю память по мере надобности можно дополнять.

В универсальной МТ лента (внешняя память) бесконечна.

Существует много различных конкретных вариаций (разновидностей) машин Тьюринга, например, машина Тьюринга с эластичной рабочей лентой, которая является удобным техническим средством для изучения грамматик (Э-машина). Ее особенности:

1. Э-машина является недетерминированной, т.е. допускает в один и тот же момент выполнение двух разных команд, в то время как классическая МТ - устройство для реализации алгоритма и не допускает выполнения двух различных команд в одном такте (детерминированная машина).

2. Э-машина имеет 2 ленты - «входную», на которой записывается исходная цепочка, которую машина в процессе работы прочитывает, не изменяя ее, и каждый символ читается только один раз; и «рабочую» ленту, на которой производится вся остальная работа. Соответственно Э-машина имеет две головки - «входную» и «рабочую».

3. Э-машина, в отличие от классической МТ, не требует, чтобы из любой конфигурации, в которой состояние машины не заключительное, она переходила в некоторую новую конфигурацию.

4. «Эластичность» рабочей ленты. Это означает, что:

а) стирая символ в ячейке рабочей ленты, машина (головка) уничтожает и саму ячейку, так что соседние с ней ячейки становятся соседними между собой («стягивание» ленты);

б) между любыми двумя ячейками рабочей ленты машина может создать новую ячейку, сразу записав в ней что-либо («растягивание» ленты). При таком способе работы отпадает надобность в «пустом символе».

Это позволяет при моделировании грамматик обходиться без сдвигов всего содержимого ленты, которое иначе пришлось бы производить на каждом шаге.

5. Наличие программы - конечного множества цепочек - инструкций, определяющих действие машины в зависимости от ее состояния и положения головок - сдвиг головок, чтение и запись символов, уничтожение и создание новых ячеек и т.д. (это - правила выводов).

Рассмотрим простейший пример реализации алгоритма сложения чисел и , записанных на ленте в виде и единиц с разделителем *. Обозначим такую запись .

Следовательно, необходимо переработать слово в слово , т.e. удалить символ * и сдвинуть одно из слагаемых, скажем, первое ко второму.

Такой алгоритм осуществляет машина Тьюринга, граф переходов управляющего устройства которой представлен на рисунке 2.3.

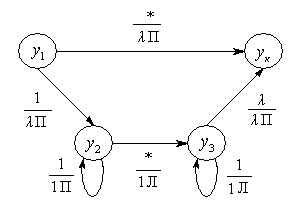
Рисунок 2.3 – Граф переходов УУ

На графе УУ, которое является автоматом Мили, обозначены - внутренние состояния.

Над дугами пишется:

• в числителе - входной сигнал (считываемый символ),

• в знаменателе - выходной сигнал (записываемый символ) и знак управления движением головки,

• стрелка (дуга) указывает состояние, в которое идет переход.

Пусть, например, заданы числа (11) и (1), Тогда последовательность работы машины может быть описана диаграммой (Рисунок 2.4).

В исходном состоянии ( ) головка установлена напротив начала первого числа (напротив первой его единицы). Головка на месте первой единицы записывает пробел и движется вправо (переход , ). Головка стоит снова против «1», идет переход , ). Головка стала против «*», идет переход , . Т.е. вместо * записали 1 (это уже ). Головка влево - напротив 1 ( ). Единица переписывается в этой ячейке, идет переход , и головка - влево. Головка напротив , значит, идет переход , . Головка делает шаг вправо и останавливается, т.к. работа закончена.

Переход на графе , необходим для случая отсутствия первого числа, т.е. когда исходное слово имеет вид .

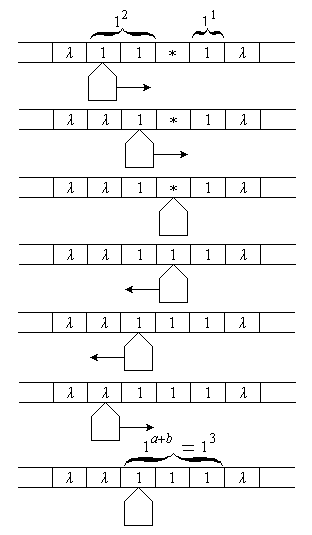
Рисунок 2.4 – Диаграмма работы МТ

Система команд имеет вид:

,

,

,

,

,

.