1.3 Класс порождающих формальных грамматик

Порождающей грамматикой называют четверку

,

где - конечное непустое множество символов, называемых терминальным (основным) словарем;

- конечное непустое множество символов, называемых нетерминальным (вспомогательным) словарем;

- конечное непустое множество правил вывода (правил переписывания, продукций); правила вывода - это грамматические правила отдельного языка-продукции;

- начальный символ.

Терминальный словарь представляет собой набор исходных символов, из которых строятся цепочки, порождаемые грамматикой.

Нетерминальный словарь - набор вспомогательных символов, обозначающих классы исходных символов.

Конечное множество - есть полный словарь грамматики .

Правила вывода - конечное непустое множество двухместных отношений вида , где и - цепочки в словаре , а “ ” интерпретируется как “заменить на”.

Цепочка непосредственно выводима из цепочки с помощью правила , если , , .

Последовательность цепочек , называется выводом (полным выводом) из , если для каждого i цепочка непосредственно выводима из . Длина вывода равна числу правил вывода. Вывод цепочки считается законченным, если не существует больше цепочки, которая следует из , т.е. состоит только из терминальных символов.

Начальный символ - выделенный нетерминальный символ, обозначающий класс языковых объектов, для которых предназначена данная грамматика. Начальный символ иногда называют целью грамматики или ее аксиомой.

Пример грамматики 1:

Пусть грамматика задана следующим образом:

; ; ;

Типичные выводы предложений:

В скобках над стрелками указан номер используемого правила вывода.

- начальный нетерминальный символ. Надо, чтобы последний вывод был цепочкой только из .

При описании естественного языка в терминах теории формальных грамматик терминальные символы интерпретируются как слова или морфемы - мельчайшие осмысленные единицы языка (корни, суффиксы и т.п.); нетерминальные символы - как названия классов слов и словосочетаний (подлежащее, сказуемое, группа глагола и т.п.). Цепочка символов обычно интерпретируется как предложение естественного языка.

Пример грамматики 2:

Пусть грамматика задана следующим образом:

;

;

.

Построим некоторые цепочки языка:

Очевидно, последняя цепочка вывода является заключительной и представляет собой предложение естественного языка.

Аналогично можно вывести цепочку ГРУЗОВАЯ МАШИНА ДОСТАВЛЯЕТ ГРУЗ и ряд других.

Заметим, что в этом примере нетерминальными символами являются синтаксические категории.

Вывод можно также описать структурным деревом, удовлетворяющим следующим требованиям:

1. каждая вершина дерева имеет в качестве метки символ из ;

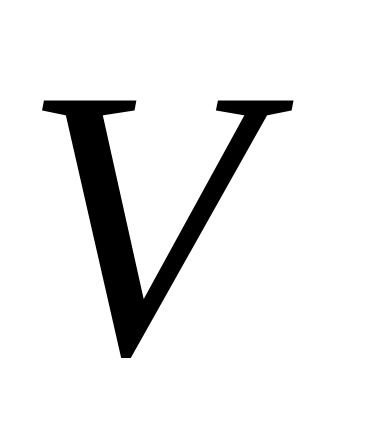2. корень дерева, т.е. вершина, в которую не входит ни одна дуга, имеет метку ;

3. если вершина с меткой Д имеет хотя бы одну подчиненную вершину, то ;

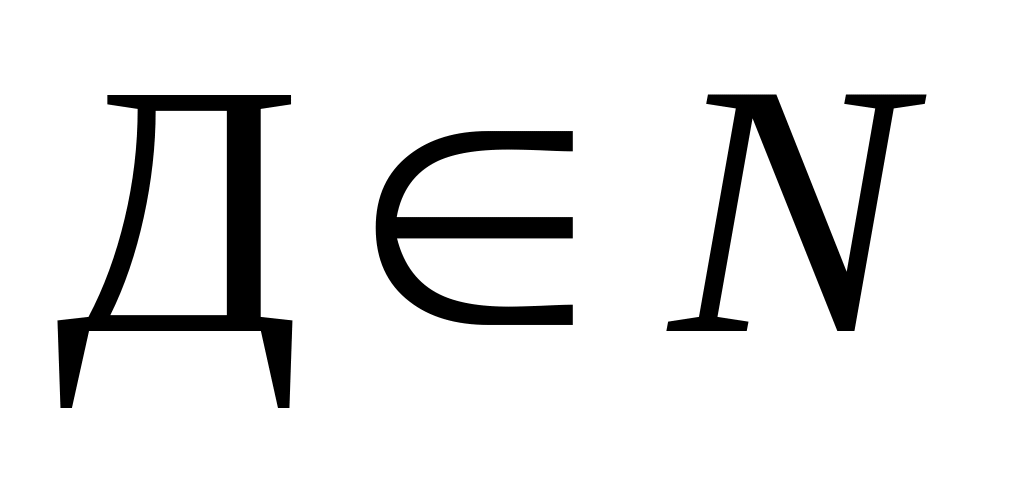4. если некоторые n вершин с метками 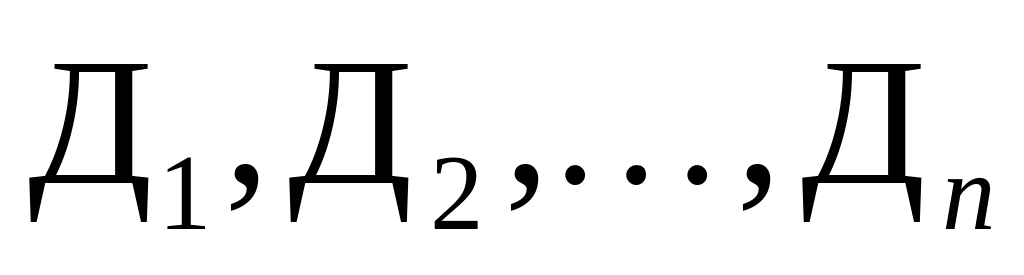подчинены непосредственно вершине с меткой Д, то в существует правило .

Структурное дерево для примера 2 изображено на схеме:

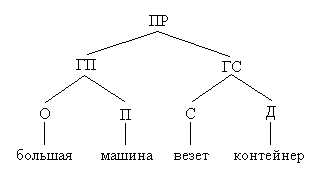
В лингвистике слова или последовательности, которые являются элементами какой-либо другой конструкции, называют составляющими. Поэтому структурное дерево называют маркером структуры составляющих или С-маркером.

Рассмотрим пример, показывающий, как можно использовать порождающую грамматику в качестве распознающей, т.е. способной определить, является ли рассматриваемая цепочка правильной в смысле данной грамматики (т.е. состоит ли она лишь из терминальных символов и математических операций).

Пример грамматики 3:

Пусть задана порождающая грамматика:

; ; ;

(знаки логического умножения (*) и сложения ( ) - можно также включить в множество терминальных символов, но чаще их просто опускают).

Проверить, является ли цепочка правильной в смысле заданной грамматики.

Очевидно, что заданная цепочка является правильной, т.к. в заданной грамматике существует вывод

Эта цепочка является правильной в смысле заданной грамматики.

Каждой грамматике однозначно соответствует язык , порожденный данной грамматикой. При этом один и тот же язык может порождаться различными грамматиками.

Итак, множество цепочек в основном (терминальном) словаре грамматики , выводимых из ее начального символа (иначе - множество последних цепочек всевозможных полных выводов в ), называют языком, порождаемым грамматикой , и обозначают .

Пример грамматики 4:

Рассмотрим порождающую грамматику с

; ; и правилами

Эта грамматика порождает язык . Например, цепочка в данной грамматике имеет вывод, на каждом шаге которого последовательно применяются продукции (правила перехода из ) 1,2,3,4,5,6,5,7,7:

Чтобы получить другие цепочки языка , нужно изменить порядок (последовательность) применения продукций.

Так, для получим цепочку :

. И так далее.