Лекция 16. Основные понятия квантовой механики

16.1. Корпускулярно-волновой дуализм

16.2. Гипотеза де Бройля. Дифракция электронов

16.3. Основные понятия квантовой механики

Теория Бора оказалась недостаточной для объяснения многих явле­ний микромира - строения многоэлектронных атомов, молекул, химической связи и т.д. Идеи де Бройля и выявленные на опыте волновые свойства частиц вещества послужили толчком к созданию принципиально новой теории, описывающей поведение микрочастиц с учетом их волновых свойств. Этой теорией стала квантовая (волновая) механика, основы которой были созданы в 1925—1926 гг. В.Гейзенбергом и Э.Шредингером. Квантовая механика раскрывает два основных свойства вещества: квантованность внутриатомных процессов и волновую природу частиц. Квантовая механика лишена наглядности, характерной для классической механики. Образы привычного нам макромира становятся непригодными для описания явлений, происходящих в микромире. При изучении явлений, происходящих в макромире, мы пользовались законами классической физики, которые остаются незыблемыми, если ограничить область их применения. Для того чтобы решить вопрос о том, какими законами механики (классическими или релятивистскими) следует пользоваться для описания рассматриваемого явления, нужно знать, с какой скоро­стью движется исследуемый объект. Если его скорость соизмерима со скоростью света в вакууме, то нужно применять релятивистские формулы. Скорость света в вакууме является критерием, определяющим гра­ницу применимости классических законов, так как она является макси­мальной скоростью передачи сигналов.

Возникает вопрос: существует ли подобный критерий при описании поведения мельчайших частиц вещества, обладающих корпускулярно-волновым дуализмом? Да, такой критерий существует, им является по­стоянная Планка.

Для того чтобы описать поведение любой частицы, нужно определить ее координату x, импульс p, энергию Е и т.д. В классической физике нет каких-либо ограничений, запрещающих с любой степенью точности одновременно измерить, например, координату х и соответствую-щую проекцию импульса р_х. В квантовой механике положение принципиально иное. Так как движущаяся частица обладает корпускулярно-волновым дуализмом, то одновременное точное определение координаты х и импульса р_х невозможно.

Тщательный анализ поведения микроскопических частиц, проведенный Гейзенбергом, показал, что существует принципиальный предел точности измерений указанных величин. Если обозначить Δх, Δу, Δz не точность (неопределенность) определения координаты, а Δр_х Δр_у, Δр_z, - неточность (неопределенность) определений соответствующих проекций импульса, то эти величины между собой связаны зависимостями:

(16.1)

Эту зависимость называют соотношением неопределенностей Гейзенберга. Из него следует: чем точнее определена координата (Δx→0), тем менее точно определен импульс (Δр_х→0), и наоборот.

Таким образом, соотношение неопределенностей устанавливает пределы, за которыми принципы классической физики становятся неприемлемыми. Если произведение ΔхΔр сравнимо с h, то поведение частицы описывается законами квантовой механики, если ΔхΔр велико по сравнению с h, то поведение частицы описывается законами классической физики. Чтобы понять, почему эксперимент не дает большей точности, чем позволяют соотношения неопределенности, предположим, что необходимо точно определить положение электрона, летящего в пучке со скоростью v, импульсом p (рис, 16.1). На пути пучка находится щель АВ шириной α. За щелью находится эк­ран CD, на котором наблюдает­ся дифракционная картина (ширина щели α сравнима с длиной волны де Бройля λ для электронов). Пунктирной линией изо­бражена плотность вероятности для центрального максимума. При дифракции от одной щели интенсивностью максимумов высшего порядка можно пренебречь по сравнению с интенсивностью центрального максимума.

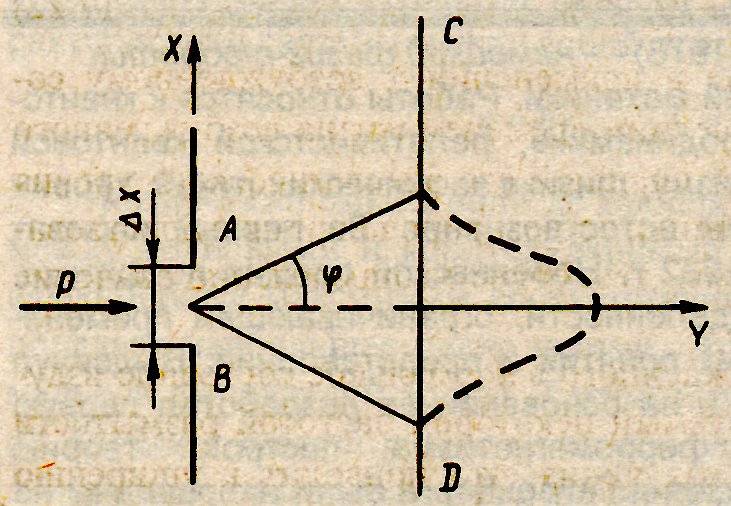
Рис. 16.1

Положение центрального максимума определяется направлением на минимумы первого порядка, т е. углом φ, определяемым из соотношения?

sinφ = 2k λ/2, где k = 1, откуда sinφ=λ/α

где, λ = h/(mv) = h/p (16.2)

Так как каждый электрон до щели движется в пучке перпендикуляр­но плоскости щели, то составляющая импульса р_x = 0, но координата х электрона неопределенная. В момент прохождения щели электрон имеет координату, равную координате щели. В определении координаты электрона содержится неопределенность, зависящая от размеров щели: Δx = α. При дифракции появляется составляющая импульса р_x, неопределенность составляющей импульса зависит от угла φ:

Δ р_x = р sinφ. (16.3)

Учитывая (16.2), получаем

Δх Δр_x = h. (16.4)

Если учесть наличие второго дифракционного максимума, то неопределенность в определении импульса увеличивается, поэтому выражение можно переписать в виде:

Δх Δр_x ≥ h. (16.5)

Соотношение, аналогичное (16.5), имеет место для времени и энергии:

ΔE Δt ≥ h. (16.6)

Рассмотрим это соотношение в применении к возбужденному состоянию атома. Если считать Δt средним временем жизни возбужденного состояния атома, а ΔЕ - средней шириной его энергетического уровня (ценность энергии состояния), то, чем короче время существования какого-либо состояния системы, тем более неопределенно значение его энергии. При переходе атома из возбужденного в нормальное состояние излучается квант энергии, характеризуемый некоторой частотой размытости Δν=ΔЕ/h спектральной линии излучения, что приводит к расширению спектральных линий.

Следует отметить, что волны де Бройля не являются электромагнитными. Они имеют особую природу, не имеющую аналогии в классической физике. Причем волны де Бройля представляют собой универсальное яв­ление для всех движущихся частиц. Гипотеза де Бройля экспериментально подтвердилась в опытах К. Дэвиссона и Л. Джермера в 1927 году, наблю­давших рассеяние электронов монокристаллом никеля.

Электронная пушка испускала пучок электронов определенней скорости, которые попадали на монокристалл ни­келя и рассеивались им. Приемником рассеянных электронов служил ци­линдр Фарадея, число электронов, попадавших в цилиндр Фарадея, было пропорционально силе тока в электрической цепи цилиндра. С точки зрения классической физики электроны рассеивались бы под всевозможными углами. Однако при наблюдении рассеяния электронов под углами оказалось, что максимум числа отраженных электронов (максимум силы тока) в электрической цепи приходился на электроны с энергией Е = 54 эВ, что соответствовало волне Де Бройля = 0,167 нм. Рассеяние электронов происходило подобно рассе­янию рентгеновских лучей при выполнении условия Вульфа-Брэгга:

. (16.7)

Таким образом, опыты Дэвиссона и Джермера подтвердили гипотезу де Бройля о существовании волновых свойств у электронов. Позднее волновые свойства электронов были подтверждены другими независимыми опытами.

В экспериментах по рассеянию электронов на кристаллах, как было показано выше, обнаруживается, что в отдельных направлениях рассеивается большее число электронов, чем во всех других. С волновой точки зрения наличие максимумов числа электронов в некоторых направлениях означает, что в этих направлениях волны де Бройля имеют наибольшую интенсивность. Учитывая, что интенсивность волны пропорциональна квадрату модуля амплитуды волны, можно дать своеобразное вероятностное толкование волн де Бройля. Квадрат модуля амплитуды А² волн де Бройля в данной точке пространства является мерой вероятности того, что частица находится в этой точке.

Для описания распределения вероятности нахождения частицы в данный момент времени в некоторой области пространства вводится функция координат и времени, которую называют волновой функцией . Волновая функция сама по себе физического смысла не имеет, смысл имеет квадрат модуля волновой функции. Опре­делим его следующим образом: вероятность того, что частица находится в элементе объема , пропорциональна квадрату модуля волновой функции  ² и элементу объема , т.е.

. (16.8)

Плотность вероятности будет равна

(16.9)

Она определяет вероятность пребывания частицы в данной точке простран­ства. Следовательно, квадрат модуля волновой функции, где комплексно сопряженная с волновая функция, представ­ляет собой вероятность нахождения частицы в данной точке простран­ства. Иными словами, величина определяет интенсивность волн де Бройля. По определению волновой функции она должна удовлетворять следующему условию:

, (16.10)

где тройной интеграл вычисляется по всему пространству от - до . Выражение означает, что нахождение частицы в какой - либо точке всего бесконечного пространства есть достоверное событие и его вероятность должна быть равна единице. Выражение называют также условием нормировки волновой функции или условием нормировки вероятностей.

ЛЕКЦИЯ 17. ОБЩЕЕ УРАВНЕНИЕ ШРЕДИНГЕРА