
- •1.1. Гармонические колебания и их характеристики
- •1.2. Пружинный маятник. Математический маятник. Физический маятник
- •2.1. Электрический колебательный контур.
- •2.2. Свободные электрические колебания
- •3.1. Затухающие колебания
- •3.2. Вынужденные колебания
- •6.1. Световая волна и ее виды
- •6.2. Основные определяющие величины
- •6.3. Характер распространения электромагнитных волн
- •7.1. Основные понятия и законы геометрической оптике 7.2. Показатели преломления среды
- •7.3. Линза и ее виды, характеристики
- •8.1.Энергетические величины в фотометрии
- •8.2. Световые величины в фотометрии
- •Лекция 9. Интерференция света
- •14.1. Фотоэффект, его виды и законы
- •14.2. Уравнение Эйнштейна для фотоэффекта
- •14.3. Эффект Комптона
- •15.1. Постулаты Бора
- •15.2. Полная энергия электрона в атоме
- •15.3. Опыт Франка-Герца.
- •Лекция 16. Основные понятия квантовой механики
- •16.1. Корпускулярно-волновой дуализм
- •16.2. Гипотеза де Бройля. Дифракция электронов
- •16.3. Основные понятия квантовой механики
- •17.1. Временное уравнение
- •17.2. Стационарное уравнение Шредингера
- •18.1. Движение частицы в одномерной потенциальной яме.
- •18.2. Прохождение частицы сквозь потенциального барьера. (Туннельный эффект)
- •20.1. Вероятность макросостояния.
- •20.2. Распределение Ферми-Дирака
- •20.3. Распределение Бозе-Эйнштейна
- •22.1. Исходные представления зонной теории твердых тел
- •22.2. Расширение энергетического уровня
- •22.3. Энергетические уровни и зоны
- •23.1. Фотопроводимость полупроводников
- •23.2. Люминесценция твердых тел
- •24.1. Контакт полупроводников p и n типов
- •24.2. Приминение p и n перехода в технике
- •24.3. Транзисторы
- •26.1. Радиоактивность и ее виды
- •26.2. Закон радиоактивного распада
- •26.3. Активность радиоактивного вещества
- •27.1. Правила смещения
- •27.2. Различные виды распадов
- •28.1. Взаимодействие заряженных частиц, нейтронов и γ-квантов со средой
- •28.2. Излучение Вавилова-Черенкова
- •28.3. Взаимодействие нейтронов с веществом
- •30.1. Термоядерные реакции
- •30.2. Условия осуществления управляемых термоядер ных реакции
- •30.3. Физика элементарных частиц.
- •Индивидуальные домашние задания
15.1. Постулаты Бора
15.2. Полная энергия электрона в атоме
15.3. Опыт Франка-Герца.
Обобщая результаты опытов, Резерфорд предложил ядерную (планетарную) модель строения атома. Согласно этой модели, весь положительный заряд и почти вся масса атома (99,4%) сосредоточены в атомном ядре. Размер ядра (~10-15 м) ничтожно мал по сравнению с размером атома (~10-10 м). Вокруг ядра по замкнутым эллиптическим орбитам, которые в первом приближении можно считать круговыми, движутся электроны, образуя электронную оболочку атома. Заряд ядра равен суммарному заряду электронов. Однако предложенная Резерфордом модель строения атома не объяснила спектральных закономерностей и даже оказалась в противоречии с законами классической механики и электродинамики. В самом деле, движение электрона по орбите, как и всякое криволинейное движение, есть движение с ускорением. Согласно законам классической электродинамики, криволинейное движение должно сопровождаться излучением света соответствующей частоты. Следовательно, при движении электрона вокруг ядра атом должен непрерывно излучать энергию. Но уменьшение энергии приводит к уменьшению радиуса орбиты электрона электрон должен двигаться по спирали, приближаясь к ядру. А так как скорость движения электрона остается неизменной, то должна увеличиться и круговая частота его вращения, непрерывно должна расти частота излучения, т.е. спектр излучения должен быть сплошным. Непрерывно приближаясь к ядру, электрон через небольшой промежуток времени должен упасть на ядро, т.е. в модели Резерфорда атом является неустойчивой системой. В действительности же атомы являются весьма устойчивыми системами и имеют линейчатые, а не сплошные спектры излучения. Внутреннее строение атома изучать непосредственно невозможно из-за малости размеров атома, линейные размеры которого приблизительно 10-10 м. Структура атома проявляется только косвенно в явлениях, связанных с его внутренним строением. К числу этих явлений относится излучение. При изучении излучения ученым удалось установить общие закономерности в характере спектров и найти ряд эмпирических законов, которым они подчиняются. Было установлено, что спектральные линии всех элементов можно разбить на ряд серий. Структуры соответствующих серий, относящихся к различным химическим элементам, схожи между собой. В пределах одной серии расположение спектральных линий имеет определенный порядок. Наиболее простым атомом является атом водорода. В 1885 г. Бальмеру удалось найти формулу, описывающую распределение спектральных линий видимого спектра водорода, получивших название серии Бальмера:
![]() (15.1)
(15.1)
λ - длина волны; 1/λ - волновое число; n для различных линий серии принимает значение последовательного ряда целых чисел, начиная с трех: n = 3,4,5, R = 1,097 107 м-1 - постоянная
Ридберга. Формула (15.1) определяет волну, соответствующую последовательным линиям серии Бальмера, как функцию целого числа. Исследования излучения в невидимой части спектра показали, что существуют серии, расположенные в инфракрасной области: серия Пашена, Брэккета, Пфунда; в ультрафиолетовой области серия Лаймана. Формулы, определяющие расположение спектральных линий в каждой из этих серий, аналогичны формуле для серии Бальмера. Обычно обобщенную формулу Бальмера для всех линий спектра атома водорода записывают в виде:
![]() (15.2)
(15.2)
где i и n принимают вполне определенные значения для каждой серии и каждой спектральной линии (табл. 15.1).
Таблица 15.1
Значение i |
Наименование серии |
Значение n |
1 2 3 4 |
Серия Лаймана Серия Бальмера Серия Пашена Серия Брэккета |
2,3,4, 3,4,5, 4,5,6, 7,8,9, |
Учитывая, что λ = c/ν или 1/λ=ν/с, формулу можно, переписать в виде
ν=R'(1/i2–1/n2) (15.3)
[R' = R c = 3,29·1015с-1. (15.4)
Величину R' также называют постоянной Ридберга. При увеличении n длина волны уменьшается, а частота линий увеличивается и достигает предельного значения R/i2 при n → ∞. R/i2 является границей серии. Аналогичные спектральные линии имеются не только у водорода, а, например, и у щелочных металлов. Расположение спектральных линий определяется формулой, аналогичной формуле Бальмера. Частота, соответствующая какой-либо спектральной линии этой серии, является разностью двух величин, одна из которых зависит от номера i серии и постоянна для всех линий данной серии, а другая определяется номером n в этой серии. Н. Бор ввел идеи квантовой теории в ядерную модель Резерфорда и разработал теорию атома водорода полностью подтвержденную экспериментально. В основе боровской теории атома лежат два основных положения (постулата).
1. Электроны могут двигаться в атоме только по определенным орбитам, находясь на которых, они, несмотря на наличие у них ускорения, не излучают. Эти орбиты соответствуют стационарным состояниям электронов в атоме и определяются условием:
mе vn rn = nh/2π (15.5)
rn - радиус n-й орбиты; vn - скорость электрона на этой орбите; mе - масса электрона; mevnrn - момент импульса электрона на этой орбите; n - целое число (n ≠ 0).
2. Атом излучает или поглощает квант электромагнитной энергии при переходе электрона из одного стационарного состояния вдругое. Энергия кванта равна разности энергий стационарных состояний электрона до (Е2) и после (Е1) перехода:
hν = E2 -E1. (15.6)
Рассмотрим простейший атом - атом водорода. Он состоит из ядра, в состав которого входит один протон, и одного электрона, вращающегося вокруг ядра по круговой орбите. На электрон со стороны ядра действует кулоновская сила притяжения, сообщая ему центростремительное ускорение, поэтому ;
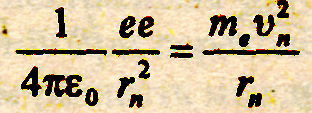 (15.7)
(15.7)
е - заряд электрона и протона, ε0 - электрическая постоянная. Поскольку должен выполняться первый постулат Бора, воспользуемся выражением (15.5). Определим из него скорость vn, возведем в квадрат и подставим в (15.7). Из полученного выражения найдем:
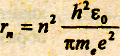 (15.8)
(15.8)
[n=1,2,3, …]. Как следует из соотношения (15.8), радиусы орбит электрона в атоме водорода пропорциональны n2. Подставляя в (7.8) значения констант и считая n = 1, получаем значение первого воровского радиуса, который является единицей длины в атомной физике:
rв = 0,528· 10-10 м.
По боровской модели ядро атома считается неподвижным, поэтому полная энергия Е атома является суммой кинетической энергии Ек вращения электрона и потенциальной энергии Еn взаимодействия электрона с ядром:
![]() (15.9)
(15.9)
Полученное значение Е отрицательно, так как потенциальная энергия двух зарядов, находящихся на бесконечно большом расстоянии, равно нулю. При сближении зарядов потенциальная энергия уменьшается.
Наименьшей энергией, как следует из уравнения (15.9), атом обладает при n=1. В этом случае говорят, что атом находится в основном энергетическом состоянии. Состояние с n>1 называют возбужденными. Определим энергию Еn на любом энергетическом уровне. Для этого подставим (15.8) в выражение (15.9):
![]() (15.10)
(15.10)
Линейчатые спектры
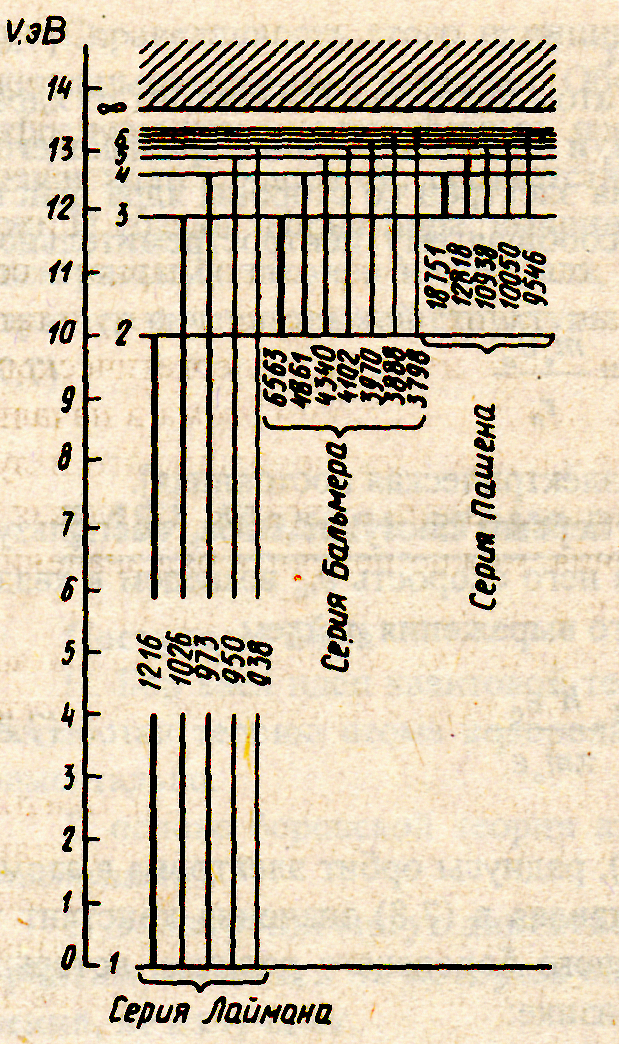
Рис.15.1.
При переходе электрона с одного энергетического уровня на другой, согласно второму постулату Бора, выделяется или поглощается квант энергии
![]() (15.11)
(15.11)
Если электрон переходит, например, со второй орбиты (n2= 2) на первую (n1 = 1), то выделяется квант энергии. В обратном случае такой же квант энергии поглощается. Таким образом, максимальную энергию атому водорода нужно сообщить для того, чтобы перевести электрон на орбиту с n = 1 на n → ∞, т.е. оторвать его от ядра атома (ионизовать атом). Из соотношения (15.11) можно определить частоту ν или длину волны λ = с/ν поглощаемого или испускаемого фотона:
![]() (15.12)
(15.12)
![]() (15.13)
сериальные формулы.
Видно, что выражение (15.12) представляет
собой обобщенную
формулу Бальмера,
а величина Ридберга.
Значение R,
вычисленное по формуле (15.14), совпадает
с экспериментальным значением этой
постоянной, что является подтверждением
правильности теории Бора для атома
водорода.
(15.13)
сериальные формулы.
Видно, что выражение (15.12) представляет
собой обобщенную
формулу Бальмера,
а величина Ридберга.
Значение R,
вычисленное по формуле (15.14), совпадает
с экспериментальным значением этой
постоянной, что является подтверждением
правильности теории Бора для атома
водорода.
![]() ( 15.14),
( 15.14),
является постоянной Ридберга.
Р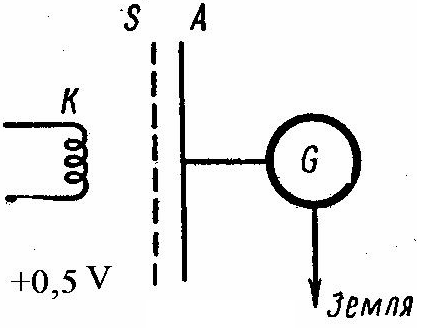 ис.15.2
.
Рис.15.3.
ис.15.2
.
Рис.15.3.
Теория Бора объяснила расхождения при экспериментальных определениях постоянной Ридберга для атома водорода и однократно ионизованного атома гели
Постулат Бора о
существовании стационарных состояний
в атомах и правило частот нашли свое
экспериментальное подтверждение в 1913
году в опытах Д. Франка и Г. Герца.
Принципиальная схема экспериментальной
установки показана на рисунке 30.2.
Раскаленный катод К в виде спирали
испускал электроны, которые под действием
электрического поля двигались к аноду
А, соединенному с гальванометром Г.
Между катодом и анодом устанавливался
сетчатый электрод
.
Вся эта система помещалась в стеклянный
баллон, из которого был откачан воздух
и вводились ртутные пары под давлением
порядка 15 Па. Между катодом и сеткой
создавалось ускоряющее электрическое
поле с разностью потенциалов
![]() , а между сеткой и анодом - слабое
замедляющее поле с разностью потенциалов
, а между сеткой и анодом - слабое
замедляющее поле с разностью потенциалов
![]() , не превышающей 0,5 В. Электроны могут
испытывать соударения с атомами ртути
двоякого рода.
, не превышающей 0,5 В. Электроны могут
испытывать соударения с атомами ртути
двоякого рода.
Первый тип соударений - упругие столкновения, которые приводят к простому рассеянию электронов без изменения величины скорости электронов. Такие упругие столкновения не могут являться причиной полного отсутствия тока в цепи, который должен возрастать с увеличением ускоряющей разности потенциалов.
Второй тип соударений
- неупругие столкновения электронов с
атомами ртути - связан с потерей
электронами их энергии и передачей этой
энергии атомам ртути. Однако, в соответствии
с постулатами Бора атом ртути не может
принять произвольную энергию, а лишь
определенную порцию энергии, равную
разности энергий на различных
энергетических уровнях. Ближайшим
к основному состоянию атома ртути
является возбужденное состояние,
имеющее разность энергий с основным
состоянием 4,86 эВ. В связи с этим, электроны,
ускоряемые полем, будут испытывать лишь
упругие столкновения до тех пор, пока
не приобретут энергию
![]() = 4,86 эВ. Как только энергия электронов
достигает 4,86 эВ, начинают преобладать
неупругие столкновения с полной передачей
энергии электроном атому ртути. Электрон,
потерявший свою энергию в результате
столкновения с атомом ртути, не может
преодолеть задерживающего поля между
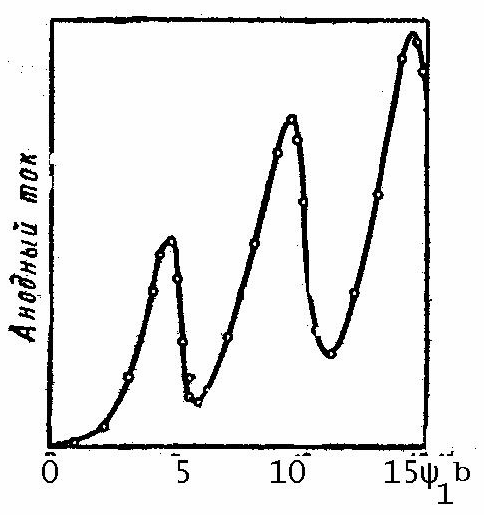
сеткой и анодом и не достигает анода.
Это приводит к резкому падению анодного
тока (рис. 30.3). Аналогичное явление будет
происходить при
= 4,86 эВ. Как только энергия электронов
достигает 4,86 эВ, начинают преобладать
неупругие столкновения с полной передачей
энергии электроном атому ртути. Электрон,
потерявший свою энергию в результате
столкновения с атомом ртути, не может
преодолеть задерживающего поля между
сеткой и анодом и не достигает анода.
Это приводит к резкому падению анодного
тока (рис. 30.3). Аналогичное явление будет
происходить при
![]() =
2
4,86 эВ и вообще говоря, при
=
=
2
4,86 эВ и вообще говоря, при
=
![]() 4,86
эВ, что подтверждает справедливость
постулатов Бора.
4,86
эВ, что подтверждает справедливость
постулатов Бора.
