Лекция 9. Интерференция света

9.1. Прицип Гюйгенса

9.1. Когерентность волны и ее виды

9.3. Условия интерференционных максимумов и

минимумов

9.4. Методы получения интерференционной картины

Волновая теория света основывается на принципе Гюйгенса: каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент времени.

Законы отражения и преломления света легко выводятся, используя принцип Гюйгенса.

П усть на границу раздела двух сред падает плоская волна (плоскость волны - АВ), распространяющаяся вдоль направления I. Пока фронт проходит расстояние ВС (за время t), фронт вторичных волн из точки А проходит расстояние AD. При отражении: ΔАВС = ΔАОС, следовательно i₁=i₁.При преломле

Рис. 9.1

нии: за время t фронт падающей волны проходит расстояние ВС =v₁t, а фронт преломленной - AD=v₂t. Из соотношения АС = BС/sin i₁ = AD/sin i₂ следует:

.

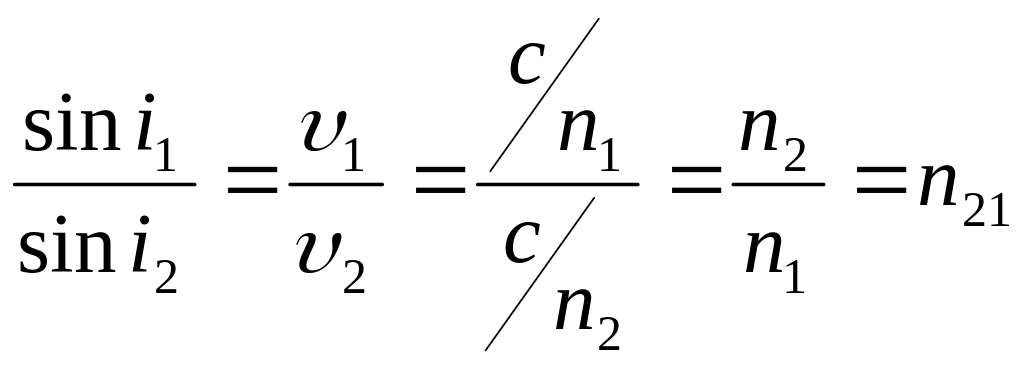Когерентность. Когерентностью называется согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.

Монохроматические волны - это неограниченные в пространстве волны одной определенной и постоянной частоты являющиеся когерентными.

Так как реальные источники не дают строго монохроматического света, то волны, излучаемые любыми независимыми источниками света всегда некогерентны. В источнике свет излучается атомами, каждый из которых испускает свет лишь в течение времени 10^-8c. Только в течение этого времени волны, испускаемые атомом, имеют постоянную амплитуду и фазу колебаний.

Немонохроматический свет можно представить в виде совокупности сменяющих друг друга коротких гармонических импульсов, излучаемых атомами - волновых цугов.

Средняя продолжительность одного цуга τ_ког называется временем когерентности.

Если волна распространяется в однородной среде, то фаза колебаний в определенной точке пространства сохраняется только в течение времени когерентности. За это время волна распространяется в вакууме на расстоянии l_ког = с τ_ког,, называемом длиной когерентности (или длиной цуга). Поэтому наблюдение интерференции света возможно лишь при оптических разностях хода, меньших длины когерентности для используемого источника света.

Временная когерентность - это определяемая степенью монохроматичности волн когерентность колебаний, совершающихся в одной и той же точке пространства. Временная когерентность существует до тех пор, пока разброс фаз в волне в данной точке не достигнет π.

Длина когерентности - расстояние, на которое перемещается волна за время когерентности.

В плоскости, перпендикулярной направлению распространения цуга волн, случайные изменения разности фаз между двумя точками увеличиваются по мере увеличения расстояния между ними. Пространственная когерентность - когерентность колебаний в один и тот же момент времени, но в разных точках такой плоскости - теряется, если разброс фаз в этих точках достигает π. Длина пространственной когерентности (радиус когерентности):

, где λ - длина волны, Δφ - разность фаз.

Источники должны быть пространственно когерентными, чтобы возможно было наблюдать интерференцию излучаемых ими световых волн.

Интерференция света - сложение в пространстве двух или нескольких когерентных световых волн, при котором в разных его точках получается усиление или ослабление амплитуды результирующей волны.

Условие интерференционного максимума:

Если оптическая разность хода Δ равна целому числу длин волн в вакууме (четному числу полуволн) , то и колебания будут происходить в одинаковой фазе.

Условие интерференционного минимума. Если оптическая разность хода Δ равна нечетному числу полуволн , то и колебания будут происходить в противофазе.

М етоды наблюдения интерференции.

До изобретения лазеров, во всех приборах когерентные световые пучки получали разделением волны, излучаемой одним источником, на две части, которые после прохождения раз-

Рис.9.2 ных оптических путей накладывали друг на друга и наблюдали интерференционную картину.

1. Метод Юнга. Свет от ярко освещенной щели S падает на две щели S₁ и S₂, играющие роль когерентных источников. Интерференционная картина ВС наблюдается на экране Э.

2 . Зеркала Френеля. Свет от источника S падает расходящимся пучком на два плоских зеркала А₁О и А₂О, расположенных под малым φ. Роль когерентных источников играют мнимые S₁ и S₂ изображения источника S. Интерференционная картина наблюдается на экране Э, Рис. 9.3

защищенном от прямого попадания света заслонкой.

Расчет интерференционной картины от двух щелей.

Д ве щели S1 и S2 находятся на расстоянии d друг от друга и являются когерентными источниками. Экран Э параллелен щелям и находится от них на расстоянии l >> d.

Интенсивность в произвольной точке A определяется разно стью хода  = S₂ - S₁ , где , Рис. 9.4 ,откуда или

Из l >> d следует , поэтому

Положение максимумов:

Положение минимумов:

Расстояние x между двумя соседними максимумами (минимумами) называется шириной интерференционной полосы

.

Интерференционная картина представляет собой чередование на экране светлых и темных полос, параллельных друг другу.

ЛЕКЦИЯ 10. ДИФРАКЦИЯ СВЕТА

10.1. Принцип Гюйгенса-Френеля

10.2. Зоны Френеля

10.3. Дифракция Френеля

10.4. дифракция Фраунгофера

10.5. Дифракционная решетка

Принцип Гюйгенса-Френеля. Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле - любое отклонение распространения волн вблизи препятствий от законов геометрической оптики.

Дифракцию объясняет принцип Гюйгенса. Именно вторичные волны огибают препятствия на пути распространения первичных волн. Френель дополнил принцип Гюйгенса представлением о когерентности вторичных волн и их интерференции. Согласно принципу Гюйгенса-Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции (сложения) когерентных вторичных волн, излучаемых вторичными (фиктивными) источниками - бесконечно малыми элементами любой замкнутой поверхности, охватывающей источник S.

Рассмотрим в произвольной

Рис.10.1

точке M амплитуду световой волны, распространяющейся в однородной среде из точечного источника S. Согласно принципу Гюйгенса-Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Φ, являющейся поверхностью фронта волны, идущей из S (поверхность сферы с центром S). Разобьем волновую поверхность Φ на кольцевые зоны такого размера, чтобы расстояния от краев зоны до M отличались на λ/2. Тогда, обозначив амплитуды колебаний от 1-й, 2-й,… m-й зон через A₁, A₂,… A_m (при этом A₁>A₂>A₃>…), получим амплитуду результирующего колебания: А=А₁-А₂+А₃-А₄+…

При таком разбиении волновой поверхности на зоны оказывается, что амплитуда колебания A_m от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон .

Тогда результирующая амплитуда в точке M будет:

,

т .к. при m >> 1 A₁ >>A_m. Площади всех зон Френеля равны , где - длина отрезка, SP₀ - радиус сферы Φ, b - длина отрезка P₀M. Радиус внешней границы m-й зоны Френеля . При =b=10 см и λ=500 нм радиус первой зоны r=0.158 мм. Следова- тельно, распространение света от S к M

Рис.10.2 происходит так, будто световой поток

распространяется внутри очень узкого канала вдоль SM , т.е. прямолинейно. Таким образом, принцип Гюйгенса-Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

Дифракция в сходящихся лучах (дифракция Френеля) - это дифракция сферических волн, осуществляемая в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию.

Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии. Амплитуда света в точке B экрана Э будет A=A₁/2±A_m/2, где знак "плюс" для случая, когда отверстие открывает нечетное число m зон Френеля, а знак "минус" - для четного m. Дифракционная картина будет иметь вид чередующихся темных и светлых колец с центром в точке B (если m - четное, то центральное кольцо будет темным, если m нечетное, то - светлым).

Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Если диск закрывает первые m зон Френеля, то амплитуда колебания в точке B экрана Э:

.

Т аким образом, в точке B всегда наблюдается интерференционный максимум (светлое пятно), соответствующий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами.

Дифракция в параллельных лучах (Дифракция Фраунгофера). Дифракция Фраунгофера наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызывающего дифракцию. Параллельный пучок лучей обычно соз

Рис. 10.3 дают, помещая точечный источник света в фокусе собирающей линзы. Дифракционную картину с помощью второй собирающей линзы, установленной за препятствием, фокусируют на экран. Рассмотрим дифракцию Фраунгофера плоской монохроматической волны на одной бесконечно длинной щели шириной a=MN. Оптическая разность хода между крайними лучами MC и ND (см. рисунок): ∆= NF sin aφ. Разобьем открытую часть волновой поверхности MN на зоны Френеля, параллельные ребру M щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна λ/2, поэтому на ширине щели уместится ∆: λ/2 зон.

В се точки волнового фронта в плоскости щели имеют одинаковую фазу и амплитуду колебаний. Поэтому суммарная интенсивность колебаний от двух любых соседних зон Френеля равна нулю. Следовательно: 1) если

Рис.10.4 число зон Френеля четное, то: ; условие дифракционного минимума; 2) если число зон Френеля нечетное, то - условие дифракционного максимума, соответствующего действию одной некомпенсированной зоны Френеля. В направлении φ=0 щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью - центральный дифракционный максимум. Направления, в которых амплитуда максимальна или равна нулю:

.

Дифракция Фраунгофера на дифракционной решетке. Одномерная дифракционная решетка - система параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

Распределение интенсивности в дифракционном спектре каждой щели, определяется направлением дифрагированных лучей и дифракционные картины, создаваемые каждой щелью, будут одинаковыми.

С уммарная дифракционная картина есть результат взаимной интерференции волн, идущих от всех щелей - в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей. Если Рис. 10.5

a - ширина каждой щели b - ширина непрозрачных участков между щелями, то величина d=a+b называется постоянной (периодом) дифракционной решетки.

Разности хода ∆ лучей, идущих от двух соседних щелей, будут для данного направления φ одинаковы в пределах всей дифракционной решетки:

.

Очевидно, что в тех направлениях, в которых ни одно из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. прежние (главные) минимумы интенсивности будут наблюдаться в направлениях

Кроме того, вследствие взаимной интерференции, в направлениях, определяемых условием

световые лучи, посылаемые двумя соседними щелями, будут гасить друг друга - возникнут дополнительные минимумы. Наоборот, действие одной щели будет усиливать действие другой, если (m=1,2,3,…) - условие главных максимумов.

ЛЕКЦИЯ 11. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГ-НИТНЫХ ВОЛН С ВЕЩЕСТВОМ

11.1. Определение понятия дисперсии

11.2. Разложение белого света в спектр

11.3. Дисперсия вещества

11.4. Электронная теория дисперсии. Поглощение

Дисперсией света называется зависимость показателя преломления n от частоты ν (длины волны λ) света (или зависимость фазовой скорости υ световых волн от его частоты ν). Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму. Дисперсия проявляется лишь при распространении немонохроматических волн.

Р ассмотрим дисперсию света в призме. Пусть монохроматический луч под углом α₁ падает на призму с показателем преломления n и преломляющим углом A. После двукратного преломле-

Рис. 11.1 ния на левой и правой гранях призмы

луч отклоняется на угол φ.

.

Если углы A и α₁ (а значит и α₂, γ₁ и γ₂) малы, то

и .

П оскольку , то откуда . Поэтому угол отклонения лучей призмой тем больше, чем больше преломляющий угол призмы. Величина называется дисперсией вещества.

Рис. 11.2

Для всех прозрачных веществ показатель преломления уменьшается с увеличением длины волны: (см. рисунок). Такая дисперсия называется Рис. 11.3

нормальной (или отрицательной). Вблизи линий и полос сильного поглощения ход кривой n(λ) — кривой дисперсии — обратный: . Такая дисперсия называется аномальной. На явлении нормальной дисперсии основано действие призменных спектрографов. Угол отклонения лучей призмой зависит от показателя преломления, который в свою очередь, зависит от длины волны. Поэтому призма разлагает белый свет в спектр, отклоняя красные лучи (длина волны больше) слабее, чем фиолетовые (длина волны меньше).

Электронная теория дисперсии Лоренца рассматривает дисперсию света как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны. Абсолютный показатель преломления среды , где ε - диэлектрическая проницаемость среды, μ - магнитная проницаемость. В оптической области спектра для всех веществ μ≈1, поэтому .

Согласно теории Лоренца, дисперсия света - следствие зависимости ε от частоты (длины волны) световых волн. По определению

,

где χ - диэлектрическая восприимчивость среды, ε₀ -электрическая постоянная, P и E - мгновенная значения поляризованности и напряженности внешнего электрического поля. В оптической области спектра частота колебаний электрического поля световой волны высока (ν≈ 10¹³Гц), поэтому ориентационная поляризация диэлектриков несущественна, и главную роль играет электронная (деформационная) поляризация - вынужденные колебания электронов под действием электрической составляющей поля световой волны.

Пусть вынужденные колебания совершает только один внешний, слабо связанный с ядром атома, электрон - оптический электрон. Его наведенный дипольный момент: p=ex, где e - заряд электрона, x - смещение электрона под действием электрического поля световой волны.

Мгновенное значение поляризованности: , где n₀ - концентрация атомов в диэлектрике. Отсюда:

.

Пусть внешнее поле E изменяется по гармоническому закону: . Тогда уравнение вынужденных колебаний электрона (без учета силы сопротивления, обуславливающей поглощение энергии падающей волны):

где - амплитудное значение силы, действующей на электрон со стороны поля волны, ω₀ - собственная частота колебаний электрона, m - масса электрона.

Решение этого уравнения: , где .

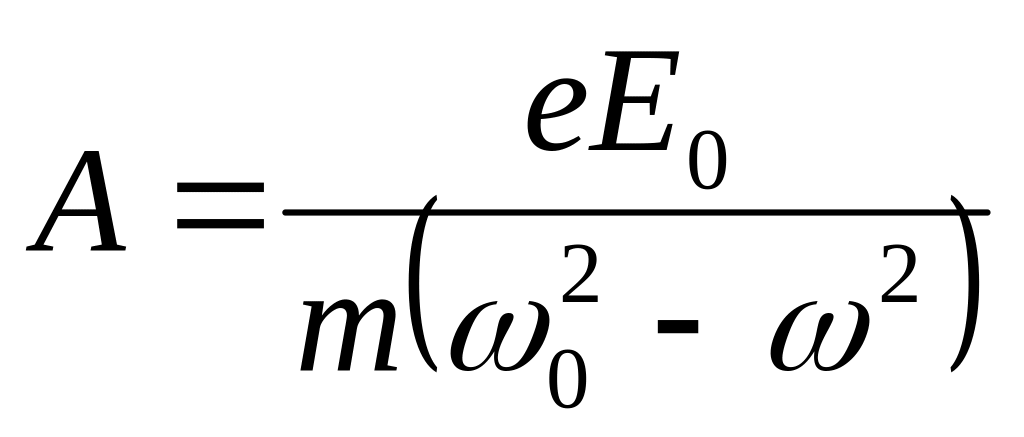Поэтому:

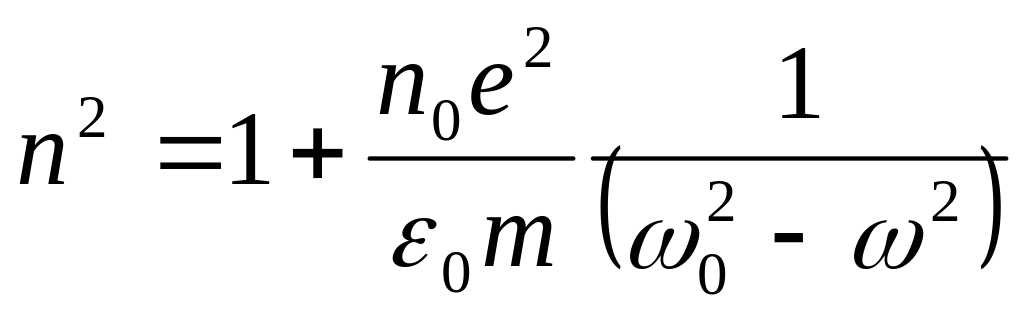
П олученная зависимость выражает явление дисперсии: . График этой зависимости приведен на рисунке. Разрыв n вблизи ω₀ обусловлен тем, что не учтены силы сопротивления среды (поглощение электромагнитных волн средой). Если учесть поглощение, то в области ω₀ зависимость n(ω) задается пунктирной линией AB - это область аномальной дисперсии (n убывает с ростом ω). Остальные участки описывают нормальную дисперсию (n растет с ростом ω). В общем случае, если в веществе

имеются различные заряды e_i

с массами m_i, совершающие вынужденные колебания с различными

собственными частотами ω_0i, то

и кривая n(ω) имеет особенности

Рис. 11.4 вблизи каждой собственной частоты ω_0i.

.

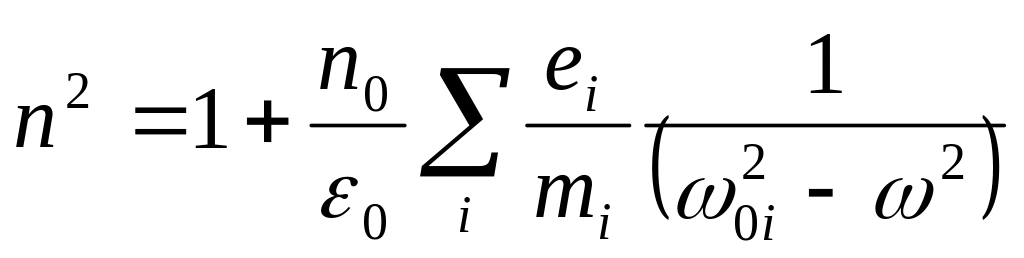Поглощение (абсорбция) света. Поглощением (абсорбцией) света называется явление уменьшения энергии световой волны при ее распространении в веществе вследствие преобразования энергии волны в другие виды энергии (внутреннюю энергию вещества, энергию вторичного излучения в других направлениях и другого спектрального состава и др.). В результате поглощения интенсивность света при прохождении через вещество уменьшается (закон Бугера):

Здесь I₀ и I - интенсивности плоской монохроматической волны на входе и выходе слоя поглощающего вещества толщиной x, α - коэффициент поглощения, зависящий от длины волны света, химической природы и состояния вещества и не зависящий от интенсивности света. Численное значение этого коэффициента α показывает толщину слоя x , равную α/1, после прохождения которого интенсивность плоской волны падает в e=2,72 раза.

ЛЕКЦИЯ 12. ПОЛЯРИЗАЦИЯ СВЕТА

12.1. Естественный свет.

12.2. Поляризованный свет

12.3. Закон Малюса.

12.4. Закон Брюстера. Вращения плоскости поляризации

При действии света на вещество основное значение имеет электрическая составляющая электромагнитного поля световой волны, поскольку именно она оказывает основное действие на электроны в атомах вещества. Поэтому для описания закономерностей поляризации будем рассматривать только световой вектор - вектор напряженности E электрического поля.

Свет представляет собой суммарное электромагнитное излучение множества независимо излучающих атомов. Поэтому все ориентации вектора E будут равновероятны. Такой свет называется естественным (рис. 12.1,а).

Поляризованным светом называется свет, в котором направления колебания вектора E каким-либо образом упорядочены.

Частично поляризованный свет (рис.12.1, б) - свет с преимущественным направлением колебаний вектора E. Плоскополяризованный свет – свет в котором вектор Er колеблется только в одной, проходящей через луч плоскости (рис. 12.1, в) и рис. (а) и (б). Эта плоскость называется плоскостью поляризации.

Закон Малюса Пропустим естественный свет с интенсивностью I_ест через поляризатор T₁ (рис. 12.2.). Поставим на пути плоскополяризованного света второй поляризатор T₂ (анализатор) под углом ψ к первому. Интенсивность I света, прошедшего через анализатор, меняется в зависимости от угла ψ по закону Малюса:

(12.1)

Рис.12.1 Рис.12.2 Рис.12.3

Естественный луч света можно представить как луч, в котором колеба­ния происходят в двух взаимно перпендикулярных направлениях, например в плоскости чертежа, которую считаем совпадающей с плоскостью падения (условно отмечаются черточками) и с плоскостью перпендикулярной (отмечаются точками). Эти два вида колебаний по-разному отражают от зеркала из диэлектрика. Если угол α падения света на границу раздела двух диэлектриков с показателями преломления n1 и n2 не равен нулю, то отраженный и преломленный лучи оказываются частично поляризованными (рис. 12.2). В отраженном луче преобладают колебания, перпендикулярные плоскости падения, в преломленном луче - колебания, параллельные плоскости падения. Степень поляризации зависит от угла падения α. При угле паде­ния, удовлетворяющем условию (закон Брюстера): tgα_полн = n₂₁ (12.2)

[n₂₁ - показатель преломления второй среды относительно первой], отраженный луч полностью поляризован, а преломленный луч поляризован только частично. Из закона Брюстера и закона преломления sinα/sinβ = n₂₁ следует, что при падении луча на диэлектрик под углом полной поляризации луч, отраженный под этим углом, и луч преломленный взаимно перпендикулярны. Выше рассмотрено явление преломления света, возникающее на границе раздела двух сред. Если одна из этих сред анизотропна, т. е. если физические свойства этой среды различны по различным направлениям, то явление преломления происходит сложнее.

Некоторые кристаллы и растворы органических соединений при прохождении сквозь них поляризованного луча поворачивают плоскость его поляризации. Это можно проследить на следующем опыте. При наблюдении источника света сквозь два николя, плоскости поляризации которых взаимно перпендикулярны, поле зрения будет темное, так как второй николь не пропустит колебаний, прошедших через первый. Поставим между николями тонкую кварцевую пластинку, вырезан­ную перпендикулярно оптической оси. Поле зрения станет светлее. Но поворотом одного из николей на некоторый угол поле зрения снова можно сделать темным. Этот опыт показывает, что при прохождении сквозь кварцевую пластинку свет остался поляризованным, но плоскость его поляризации повернулась на некоторый угол φ. Само явление получило название вращение плоскости поляризации. Вещества, вращающие плоскость поляризации, называют оптически активными. К их числу принадлежит, например, раствор сахара. В твердых телах угол φ поворота плоскости поляризации пропор­ционален длине пути светового луча в теле:

φ = [α]l (12.3)

[α] - вращательная способность (удельное вращение), зависящая от рода вещества, температуры, и длины волны]. Для растворов угол поворота плоскости поляризации равен

φ = [α]сl (12.4)

где [α] - удельное вращение; с - концентрация оптически активного вещества] Величина α зависит от природы оптически активного вещества и растворителя, температуры и длины волны света. Явление вращения плоскости поляризации нашло применение для определения концентрации какого-либо активного вещества в растворе. Так как угол поворота пропорционален концентрации оптически активного вещества и толщине слоя l, то, используя соотношение (12.4), можно определить концентрацию.

ЛЕКЦИЯ 13. КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ

13.1. Тепловое излучение

13.2. Проблемы излучения абсолютно черного тела

13.3. Квантовая гипотеза и формула Планка

13.4. Энергия и импульс световых квантов

Электромагнитное излучение, возникающее за счет внутренней энергии излучающего тела и зависящее только от температуры и химических свойств тела, называется тепловым излучением.

Тепловое излучение тел, находящихся в термодинамическом равновесии, называется равновесным излучением или температурным. В термодинамическом равновесии тепловое излучение, тел компенсируется поглощением такого же количества энергии падающего на него излучения.

Лучеиспускательной способ­ностью Е(v,T) тела называется энергия электромагнитного излучения _изл , испускаемого с единицы площади поверхности тела за единицу времени в интервале частот от до . Таким образом

(13.1)

Лучеиспускательная способность в системе СИ выражается в Дж/м².

Для спектральной характеристики поглощения электромагнитных волн телом вводится понятие поглощательной способности тела . Поглощательная способность показывает, какая доля энергии , падающей на единицу площади поверхности тела за единицу времени в интервале частот от до поглощается телом, т.е.

(13.2)

Как поглощательная, так и лучеиспускательная способности твердого тела зависят от частоты излучаемых или поглощаемых волн, от температуры тела, от его химического состава и состояния поверхности. Если тело полностью поглощает падающую на него энергию электромагнитного излучения при любой температуре и для всех частот, то такое тело называют абсолютно черным. Поглощательная способность абсолютно черного тела по определению равна единице .

Лучеиспускательная способность абсолютно черного тела зависит только от частоты и абсолютной температуры. Реальные тела не являются абсолютно черными. Достаточно хорошим приближением абсолютно черного тела являются сажа, платиновая чернь, черный бархат. Наиболее близкой моде-лью абсолютно черного тела является поверхность малого отверстия в непрозрачной стенке замкнутой полости. При каждом отражении от стенок полости происходит частичное поглощение энергии световой волны и при многократном отражении свет практически не выходит наружу. Запишем связь между электромагнитным излучением _изл , испускаемым с единицы площади поверхности тела за единицу времени в интервале частот от до и спектральной плот­ностью энергетической светимости , а также между излучаемой и поглощаемой энергии, исходя из соотношений (13.1) и (13.2):

(13.3)

В состоянии термодинамического равновесия _изл Для абсолютной черной пластины имеем:

. (13.4)

Учитывая, что в состоянии термодинамического равновесия , окончательно получаем:

или (13.5)

Таким образом, отношение лучеиспускательной способности тела к его поглощательной способности не зависит от химического состава тела и равно лучеиспускательной способности абсолютно черного тела и яв­ляется функцией температуры и частоты . Этот закон был впервые установлен Кирхгофом и носит его название, а функция называется функцией Кирхгофа. Из закона Кирхгофа следует, что, если , то , если , то . Следовательно, если тело не поглощает при данной температуре в данном интервале частот, то оно не может и излучать при этой же температуре и этом же интервале частот.

Полная мощность излучения по всему спектру частот от 0 до называется энергетической светимостью тела или интегральной излучательной способностью, которая обозначается . По определению она равна:

или с учетом закона Кирхгофа

. (13.6)

Для абсолютно черного тела , следовательно:

. (13.7)

В дальнейшем основной задачей теории теплового излучения стало отыскание явного вида функции Кирхгофа. В 1879 году на осно­ве анализа опытных данных Д. Стефан пришел к заключению, что энер­гетическая светимость любого тела прямо пропорциональна четвертой степени абсолютной температуры. Однако Л. Больцман в 1884 году теоретически методом термодинамики показал, что это утверждение спра­ведливо только абсолютно черных тел. Эта зависимость вошла в историю физики как закон Стефана-Больцмана

(13.8)

Коэффициент пропорциональности Вт/м²К⁴ носит название постоянной Стефана-Больцмана. Однако они не решили задачу об отыскании явного вида функции Кирхгофа.

Следующий шаг в нахождении явного вида функции Кирхгофа был предпринят В. Вином в 1893 году, который рассмотрел задачу об адиа­батическом сжатии излучения абсолютно черного тела в цилиндрическом сосуде с подвижным зеркальным поршнем и зеркальными стенками. В ре­зультате он получил следущее выражение для функции Кирхгофа:

(13.9)

где - некоторая неизвестная в явном виде функция.

Хотя сам В. Вин не установил явного вида функции, однако из формулы Вина (13.9) вытекает закон Стефана-Больцмана.

И з опытов было известно, что зависимость лучеиспускательной способности абсолютно черного тела от частоты при различных температурах имеет вид, показанный на рисунке 13.

Рис. 13.1 Рис. 13.2

Из этого рисунка видно, что с ростом температуры увеличивается максимальное значение лучеиспускательной способности абсолютно черного тела. Кроме того, сам максимум лучеиспускательной способнос­ти черного тела смещается с ростом температуры в сторону более вы­соких частот. Формула В.Вина позволила сформулировать эти явления в виде законов Вина. При данной температуре частота излучения , на которую приходится максимум лучеиспускательной способности абсолютно черного тела легко определяется из условия равенства нулю частной производной от функции Кирхгофа:

. (13.10)

Из последнего равенства следует:

Окончательно получаем закон смещения Вина:

, (13.11)

который гласит, что частота, соответствующая максимальному значению лучеиспускательной способности абсолютно черного тела, прямо пропорциональна его абсолютной температуре. - постоянная величина, зависящая от явного вида функции Вина . Обычно закон смещения Вина записывают через длину волны излучения

(13.12)

длина волны, на которую приходиться максимум лучеиспускательной способности абсолютно черного тела с ростом температуры смещается в сторону коротких длин волн. Постоянная мК носит название постоянной Вина, определяется опытным путем.

Впервые выражение для функции Кирхгофа было дано в работах Д. Рэлея и Д. Джинса, которые были основаны на представлениях Максвелла и методах статистической физики. Обозначая через среднее во времени значение энергии осциллятора с собственной частотой при температуре системы Т, можно представить функцию Кирхгофа в виде:

. (13.14)

Из, курса классически статистической физики известно, что на одну степень свободы колебательного движения в среднем приходится энергия, равная

.

Подставляя эту энергию в формулу (13.14), окончательно получаем формулу Рэлея и Джинса в вид

. (14.15)

Однако формула Рэлея и Джинса достаточно хорошо согласовывалась с опытом только в области низких частот (рис. 13.2).

В области же высоких частот (коротких длин волн) формула Рэлея и Джинса резко расходится с экспериментальными значениями . Это значи­тельное расхождение теории и опыта при высоких частотах получило название «ультрафиолетовой катастрофы». Кроме того, энергетическая светимость абсолютно черного тела на основе представлений Рэлея и Джинса оказалась равной

.

Таким образом, формула Рэлея и Джинса находилась в противоречии с законом Стефана-Бoльцмана, согласно которому . Выход был найден немецким физиком М. Планком в 1990 году. Он не отвергает идеи Рэлея и Джинса об излучении энергии независимыми осцилляторами. Вместе с тем, Планк предположил, что энергия излучения может принимать лишь определенные дискретные значения, равные целому числу элементарных порций энергии - квантов . Следовательно, энергию осциллятора можно представить в виде , где - любое целое положительное число. При этом условии, используя распределение Больцмана, Планку удалось найти среднюю энергию гармонического квантового осциллятора в виде:

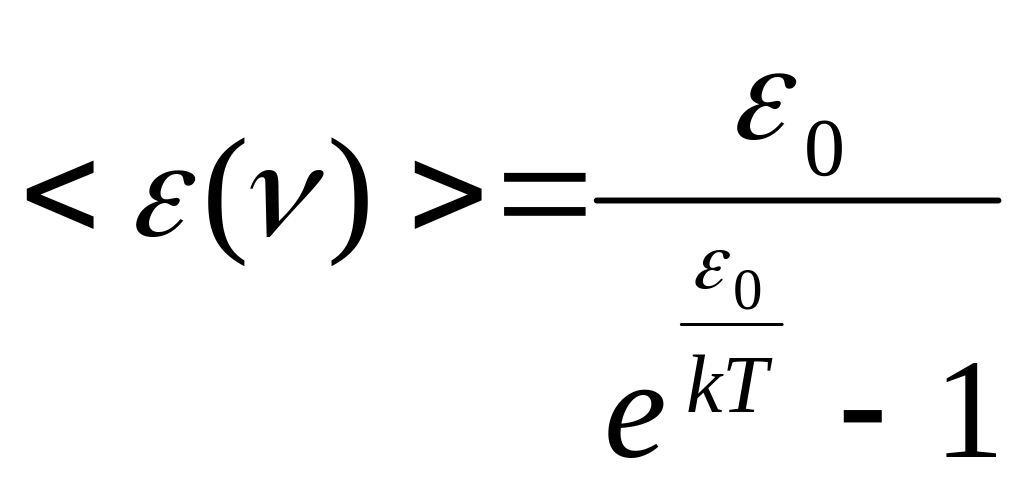. (13.16)

Подставляя среднее значение энергии гармонического осциллятора в формулу Рэлея и Джинса, получим:

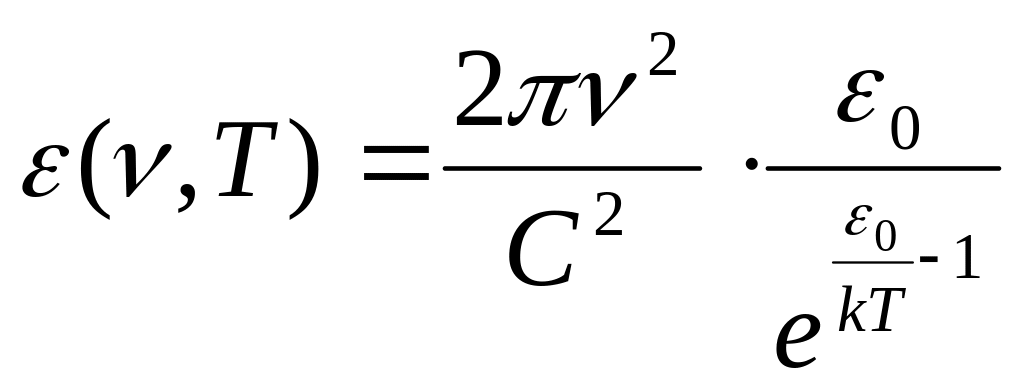. (13.17)

Сравнивая эту формулу с формулой Вина (13.9), Планк установил, что энергия кванта должна быть равна , где - постоянная Планка.

Джс

Окончательно Планк получил в явном виде выражение для функции Кирхгофа в виде:

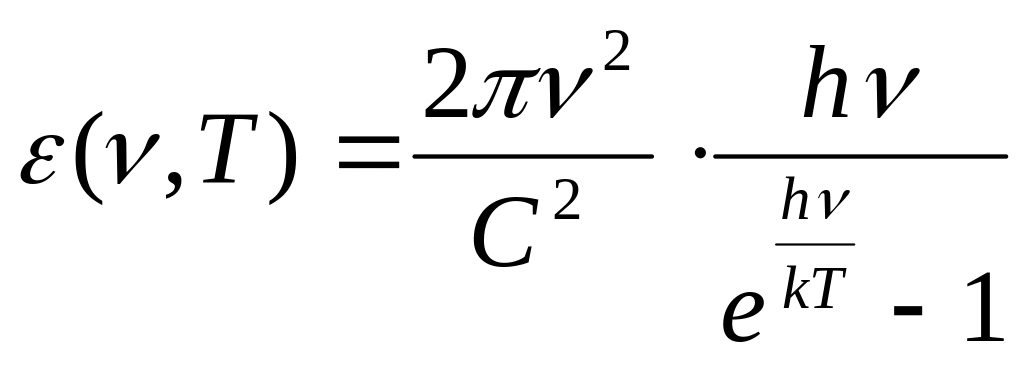. (13.18)

Формула Планка (13.18) для лучеиспускательной способности абсолютно черного тела хорошо согласуется с опытом при самых различных температурах.

ЛЕКЦИЯ 14. ФОТОЭФФЕКТ. ЭФФЕКТ КОМПТОНА