СОДЕРЖАНИЕ

Введение		4
Лекция1.	Свободные колебания	5
Лекция 2.	Электрический колебательный контур	9
Лекция 3.	Затухающие и вынужденные колебания	11
Лекция 4.	Переменный ток	14
Лекция 5.	Волны в упругой среде	17
Лекция 6.	Электромагнитные волны	20
Лекция 7.	Геометрическая оптика	22
Лекция 8.	Фотометрия	26
Лекция 9.	Интерференция света	28
Лекция 10.	Дифракция света	32
Лекция 11.	Взаимодействие электромагнитных волн с веществом	36
Лекция12.	Поляризация света	40
Лекция 13.	Квантовая природа излучения	43
Лекция 14.	Фотоэффект. Эффект Комптона	50
Лекция 15.	Строение атома	53
Лекция 16.	Основные понятия квантовой механики	61
Лекция 17.	Общее уравнение Шредингера	67
Лекция 18.	Описание движения свободных и связанных частиц в квантовой механике	70
Лекция 19.	Квантовая физика атомов и молекул	75
Лекция 20.	Квантовые статистики	82
Лекция 21.	Рентгеновские спектры. Молекулярные спектры.	88
Лекция 22.	Элементы физики твердого тела	92
Лекция 23.	Фотопроводимость полупроводников. Люминесценция твердых тел	96
Лекция 24.	Контакт электронного и дырочного полупроводников. P-n-переход. Транзисторы	98
Лекция 25.	Строение и важнейшие свойства атомных ядер	100
Лекция 26.	Радиоактивное излучение и его виды	108
Лекция 27.	Правила смещения. Альфа-распад. Бета-распад	111
Лекция 28.	Приборы для регистрации радиоактивных излучений	116
Лекция 29.	Ядерные реакции и их основные типы.	120
Лекция 30.	Реакции синтеза атомных ядер. Фундаментальные взаимодействия. Элементарные частицы	128
Задание 1	Колебания и волны	131,
Задание 2	Оптика	139
Задание 3	Квантовая физика	148
Задание 4	Атом и элементарные частицы	155

Введение

Основная цель преподавания физики состоит в:

- формировании у студентов представления о современной физической картине мира и на­учного мировоззрения;

- формировании у студентов знаний и умений использования фундаментальных законов, теорий классической и современной физики, а также методов физического исследования как основы системы профессиональной деятельности.

Задачи курса физики состоят в следующем:

- раскрыть сущность основных представлений, законов, теорий классической и современной физики в их внутренней взаимосвязи и целостности, так как для будущего инженера важно не столько описание широкого круга физических явлений, сколько усвоение иерархии физиче­ских законов и понятий, границ их применимости, позволяющее эффективно использовать их в конкретных ситуациях;

- формирование у студентов умений и навыков решения обобщённых типовых задач дисцип­лины (теоретических и экспериментально-практических учебных задач) из различных облас­тей физики как основы умения решать профессиональные задачи;

- формировать у студентов умение оценивать степень достоверности результатов, получен­ных с помощью экспериментальных или теоретических методов исследований;

- способствовать развитию у студентов творческого мышления, навыков самостоятельной познавательной деятельности, умения моделировать физические ситуации с использованием компьютера;

- ознакомить студентов с современной измерительной аппаратурой, выработать умения и на­выки проведения экспериментальных исследований и обработки их результатов, умения вы­делить конкретное физическое содержание в прикладных задачах будущей специальности.

Изучению курса физики должно предшествовать изучение: курса химии, курса высшей математики.

ЛЕКЦИЯ 1. СВОБОДНЫЕ КОЛЕБАНИЯ

 

1.1. Гармонические колебания и их характеристики

1.2. Пружинный маятник. Математический маятник. Физический маятник

Колебаниями называются движения или процессы, которые обладают определенной повторяемостью во времени. Колебания сопровождаются попеременным превращением энергии одного вида в энергию другого вида. Различают механические, электромагнитные и др. колебания. В технике и окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через равные промежутки времени. Такие процессы называют колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения. Для механических систем в описывающих их уравнениях типа (1) можно считать, что вторая производная х представляет приведенную силу инерции, а правая часть — возникающую в системе силу, связанную только с положением рассматриваемой массы (например, упругую силу), и обе они отнесены к единице массы.

Простейшим колебательным движением является гармоническое, т.е. такое колебание, при котором какая-либо характеристика системы изменяется со временем по закону синуса (или косинуса). Такая система называется гармоническим осциллятором. Гармоническое колебание величины s описывается уравнением типа

s = Acos(ωt + φ) (1.1)

где: A – амплитуда колебания – максимальное значение колеблющейся величины; ω – круговая (циклическая) частота; φ - начальная фаза колебания в момент времени t=0; (ωt + φ) – фаза колебания в момент времени t.

Дифференциальное уравнение гармонических колебаний записывается в виде

s + ω²s = 0 (1.2)

Его решением является уравнение (2).

Колебания происходят под действием возвращающей силы, т.е. силы, направленной в сторону положения равновесия и увеличивающейся по мере отклонения тела от положения равновесия. При этом гармоническими называются такие колебания, для которых возвращающая сила F прямо пропорциональна отклонению x тела от положения равновесия:

F = -kx (1.3)

Такая сила называется «упругой», причем характер колебаний определяется не только возвращающей силой, но и теми условиями, при которых эти колебания начались.

К уравнению типа (3) приводится, например, уравнение гармонического осциллятора

(1.4)

Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Как было отмечено выше, простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением

x = xm cos (ωt + φ0).

Здесь x - смещение тела от положения равновесия, x_m - амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω - циклическая или круговая частота колебаний, t - время. Величина, стоящая под знаком косинуса φ = ωt + φ₀ называется фазой гармонического процесса. При t = 0 φ = φ₀, поэтому φ₀ называют начальной фазой. Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Физическая величина, обратная периоду колебаний, называется частотой колебаний:

Частота колебаний f показывает, сколько колебаний совершается за 1 с. Единица частоты - герц (Гц) - частота периодического процесса, при котором за 1 секунду совершается один цикл колебаний. Частота колебаний f связана с циклической частотой ω и периодом колебаний T соотношениями:

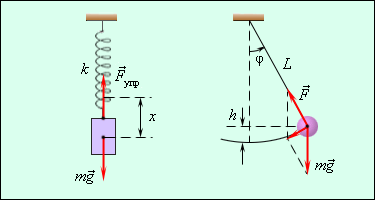
Примерами простых колебательных систем могут служить груз на пружине или математический маятник (рис. 1).

Рис. 1 1 Механические колебательные системы

Для идеального математического маятника с длиной подвеса и массой m, находящегося в поле тяготения с ускорением g, хорошим приближением является небольшой тяжелый шарик, подвешенный на тонкой длинной нити. При малых углах отклонения φ можно считать, что отклонение маятника x = lφ. Возвращающая сила:

F = mgsinφ = mgφ = mgx/l (1.5)

Уравнение движения (4) запишется в виде:

mx = -F = - -mgx/l или: x + gx /l = 0 (1.6)

Таким образом, движение математического маятника описывается дифференциальным уравнением гармонических колебаний (1.2) и происходят по закону (1.1).

Собственная частота ω и период колебаний зависят от свойств колеблющейся системы. Например, при малых колебаниях математического маятника они выражаются через ускорение свободного падения g и длину маятника l:

ω = √g/l; T = 2π√l/g (1.7)

В случае пружинного маятника груз массой m, подвешенный на абсолютно упругой пружине, совершает гармонические колебания по закону (4). Уравнение движения маятника:

mx = - kx или: x +kx/m = 0 (1.8)

Сравнивая это уравнение с уравнением (1.2) можно видеть, что пружинный маятник также совершает колебания по закону (1.1) с собственной частотой и периодом, выражаемыми при малых колебаниях грузика через его массу m и коэффициент жесткости пружины k:

ω = √k/m; T = 2π√m/k (1.9)

Физический маятник - это твердое тело, совершающее колебание вокруг горизонтальной оси, проходящей через точку подвеса, расположенную выше его центра тяжести. При малых колебаниях физический маятник совершает гармонические колебания α = α₀ · cos(ωt + φ) с циклической частотой и периодом:

ω= √mgl/J; T = 2π√J/mgl = 2π√L/g, (1.10)

где длина L = J/ml - называется приведенной длиной физического маятника; J - момент инерции маятника относительно оси, проходящей через точку подвеса маятника.

Скорость υ = υ_x движения тела определяется выражением

Появление слагаемого +π / 2 в аргументе косинуса означает изменение начальной фазы. Максимальные по модулю значения скорости υ = ωx_m достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = a_x тела при гармонических колебаниях:

Знак минус в этом выражении означает, что ускорение a(t) всегда имеет знак, противоположный знаку смещения.

ЛЕКЦИЯ 2. ЭЛЕКТРИЧЕСКИЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР