§ 13.2. Динамика твердого тела

Задача 1. Вычислить момент инерции J_c однородного стержня массой m и длиной L относительно оси, перпендикулярной стержню и проходящей через его середину. Поперечными размерами стержня пренебречь.

Дано: m, L.

J_c – ?

Решение.

Поскольку мы пренебрегаем поперечными размерами стержня (а, значит, и площадью его поперечного сечения), то масса стержня будет определяться только его длиной. Для однородного стержня его масса, приходящаяся на единицу длины, очевидно, равна . Это – так называемая линейная плотность.

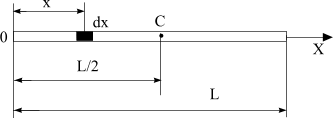
Совместим ось Х со стержнем так, как показано на рисунке и выберем в пределах стержня произвольную точку х. Тогда dx – это элементарная длина стержня в окрестности выбранной точки. Для того, чтобы вычислить элементарную массу dm выбранного кусочка стержня, надо линейную плотность стержня умножить на эту длину dx, то есть

dm =

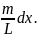
Теперь найдем момент инерции dJ этой элементарной массы относительно указанной в условии задачи оси (на рисунке точка С – середина стержня). По определению этот момент инерции равен произведению dm на квадрат расстояния до выбранной оси. Это расстояние, как видно из рисунка, равно – x. Тогда

dJ = 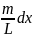(L/2 – x)².

Чтобы найти момент инерции всего стержня относительно указанной оси, надо (опять же, по определению) сложить моменты инерции всех элементарных масс стержня, то есть, просуммировать эти моменты в пределах от 0 до L. Другими словами, учитывая равномерное распределение массы стержня по его длине, надо взять интеграл от dJ в указанных пределах, то есть

J_c = = .

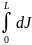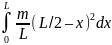Постоянную величину выносим за знак интеграла и возводим в квадрат то, что стоит в скобках. Тогда

J_c = .

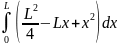Далее:

J_c = .

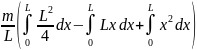Опять же выносим постоянные величины за знаки интегралов.

J_c = .

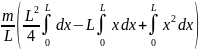Все интегралы табличные.

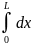= L,

= ,

= .

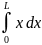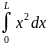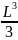Тогда

J_c = = .

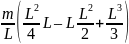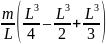Выполнив вычисления в скобках, получим 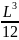. Следовательно,

J_c = 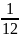m .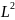

Ответ: J_c = m .

Задача 2. Доказать, что момент инерции J относительно некоторой оси равен сумме момента инерции J_c относительно оси, проходящей через центр масс параллельно данной и произведения массы m тела на квадрат кратчайшего расстояния а между этими осями, то есть J = J_c + ma². Доказательство выполнить для однородного стержня (см. предыдущую задачу).

Решение.

Перед решением этой задачи еще раз прочитайте условие и решение предыдущей задачи.

Пусть ось, относительно которой необходимо определить момент инерции тела, проходит через точку А (см. рисунок). Эта ось параллельна оси, проходящей через середину стержня. Для однородного стержня его середина является центром масс.

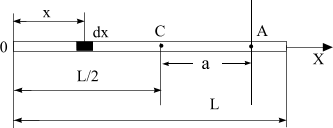
Элементарная масса dm находится от точки А на расстоянии а + – x. Тогда момент инерции dL этой элементарной массы относительно оси, проходящей через точку А, равен

dJ = dm .

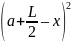Поскольку dm = dx, то

dJ = 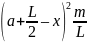dx

Момент инерции всего тела J = = .

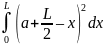Перед тем, как брать интеграл, возведем в квадрат выражение, стоящее в скобках.

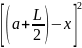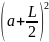
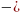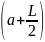= = 2 x + =

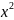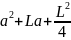
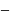= 2ax – Lx + . Тогда

J = .

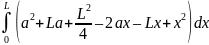J = .

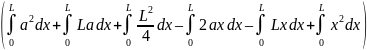Выносим постоянные величины за знаки интегралов.

J =

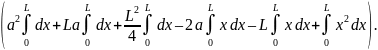
Все интегралы табличные. Первый, второй и третий интегралы дают в указанных пределах L. Четвертый и пятый интегралы дают . Последний интеграл равен . Тогда

J = .

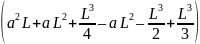Выполнив вычисления в скобках, получим

J = .

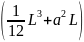Раскрываем скобки.

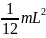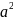J = + m . Но 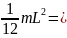J_c. Тогда

J = J_c + ma².

Доказательство было выполнено для однородного стержня с пренебрежением его поперечных размеров. Однако можно показать (мы этого делать не будем), что полученная формула справедлива и для любого тела. Эта формула является математическим выражением известной теоремы Штейнера (иногда, правда редко, ее называют теоремой Штейнера – Гюйгенса). Ценность этой теоремы заключается в том, что вычисление момента инерции тела относительно произвольной оси (а это бывает необходимо при решении различных задач) сводится, по сути, к вычислению момента инерции относительно оси, проходящей через центр масс, что не представляет принципиальных трудностей, особенно для симметричных и однородных тел.

Ответ: J_c = m .

Задача 3. Вычислить момент инерции J однородного стержня массой m и длиной L относительно оси, перпендикулярной стержню и проходящей через его конец. Поперечными размерами стержня пренебречь.

Дано: m, L.

J – ?

Решение.

Вначале ознакомьтесь с условием и решением задачи 13.2.1. Ось, относительно которой необходимо найти момент инерции тела проходит через точку В конца стержня (см. рисунок).

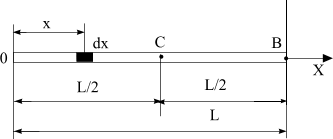
Элементарная масса dm находится от точки В на расстоянии L – x. Тогда момент инерции этой элементарной массы dJ = dm (L – x)². Поскольку dm = dx, то

dJ = dx (L – x)² = (L² – 2Lx + x²) dx.

Момент инерции всего тела

J = = 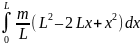= 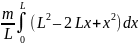. Или

J = .

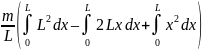Взяв интегралы, получим

J = 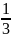mL².

А теперь решим эту задачу, используя теорему Штейнера J = J_c + ma².

В данном случае a = . Учитывая, что J_c = 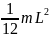, сразу находим J:

J = + m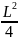 = 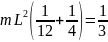mL².

Вот так, быстро и просто.

Ответ: J = mL².

Задача 4. Вычислить моменты инерции однородной прямоугольной пластины массой m, длиной а и шириной b относительно осей, проходящих вдоль краев пластины. Толщиной пластины пренебречь.

Дано: m, a, b.

J_a – ? J_b – ?

Решение.

Выберем координатные оси так, как показано на рисунке.

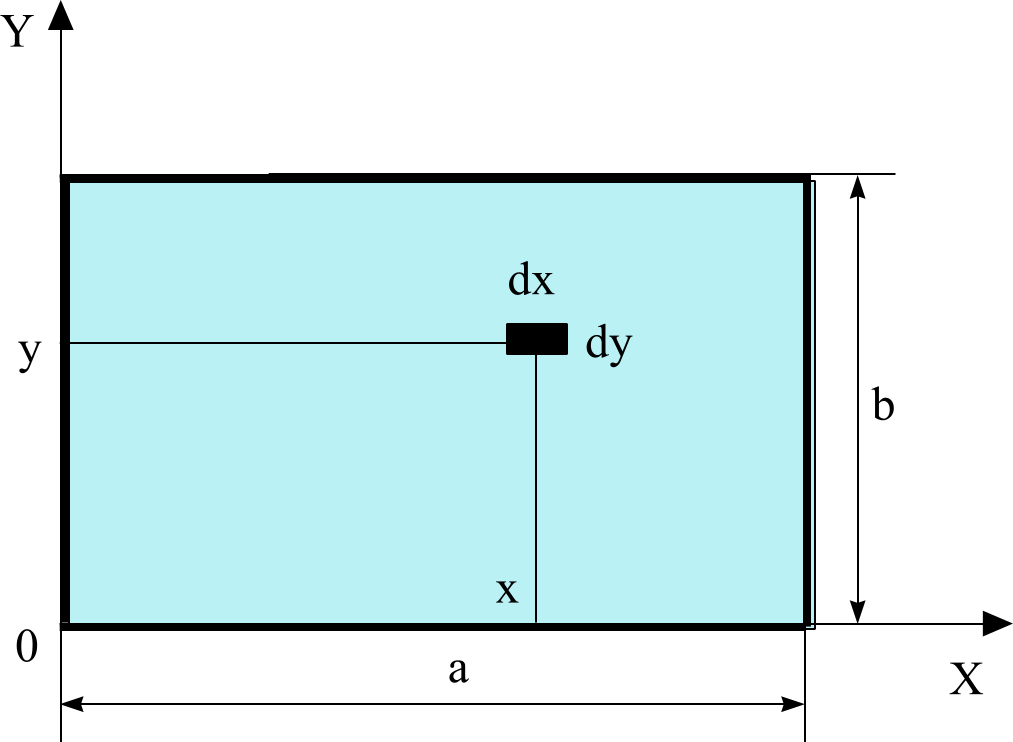
Выделим бесконечно малый элемент пластины размерами dx и dy. Площадь этого элемента dS = dx dy. Масса единицы площади пластины равна 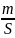= 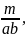где S = ab – площадь всей пластины). Это – так называемая поверхностная плотность пластины. Чтобы найти массу любого элемента пластины, надо ее поверхностную плотность умножить на площадь этого элемента. В частности, масса dm выделенного кусочка пластины будет равна dm = 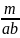ds или dm = dx dy. Его момент инерции dJ_x относительно оси Х

dJ_x = dm y² = dx dy y².

Чтобы найти момент инерции всего тела относительно данной оси, надо просуммировать момент инерции выделенного элемента по всей пластине. А для этого надо взять интеграл от последнего выражения как в пределах от 0 до а, так и в пределах от 0 до b. Записывается это так:

J_x = .

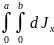Такая запись носит название двойного интеграла. Как видите, в сущности этого понятия ничего сложного нет. Перечитайте еще раз предыдущую часть решения, если остались какие-то «непонятки», но по-моему, я объяснил доступно. Идем дальше.

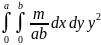J_x = или J_x = .

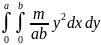Постоянную величину выносим за знаки интегралов.

J_x =

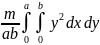
Для вычисления двойного интеграла формулу записывают вот так:

J_x =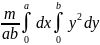 , то есть «отделяют мух от котлет».

Далее вычисляем отдельно каждый интеграл в соответствующих пределах.

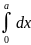= a, .

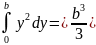Тогда

J_x = a = .

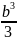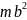Аналогично вычисляется момент инерции пластины относительно оси Y. Проведите сами нужные действия. Вы должны получить следующую формулу:

J_y = .

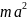Ответ: J_x = , J_y = .

Задача 5. Вычислить момент инерции J однородного плоского диска относительно оси, перпендикулярной плоскости диска и проходящей через его центр. R и m – радиус и масса диска соответственно. Толщиной диска пренебречь.

Дано: R, m.

J – ?

Решение.

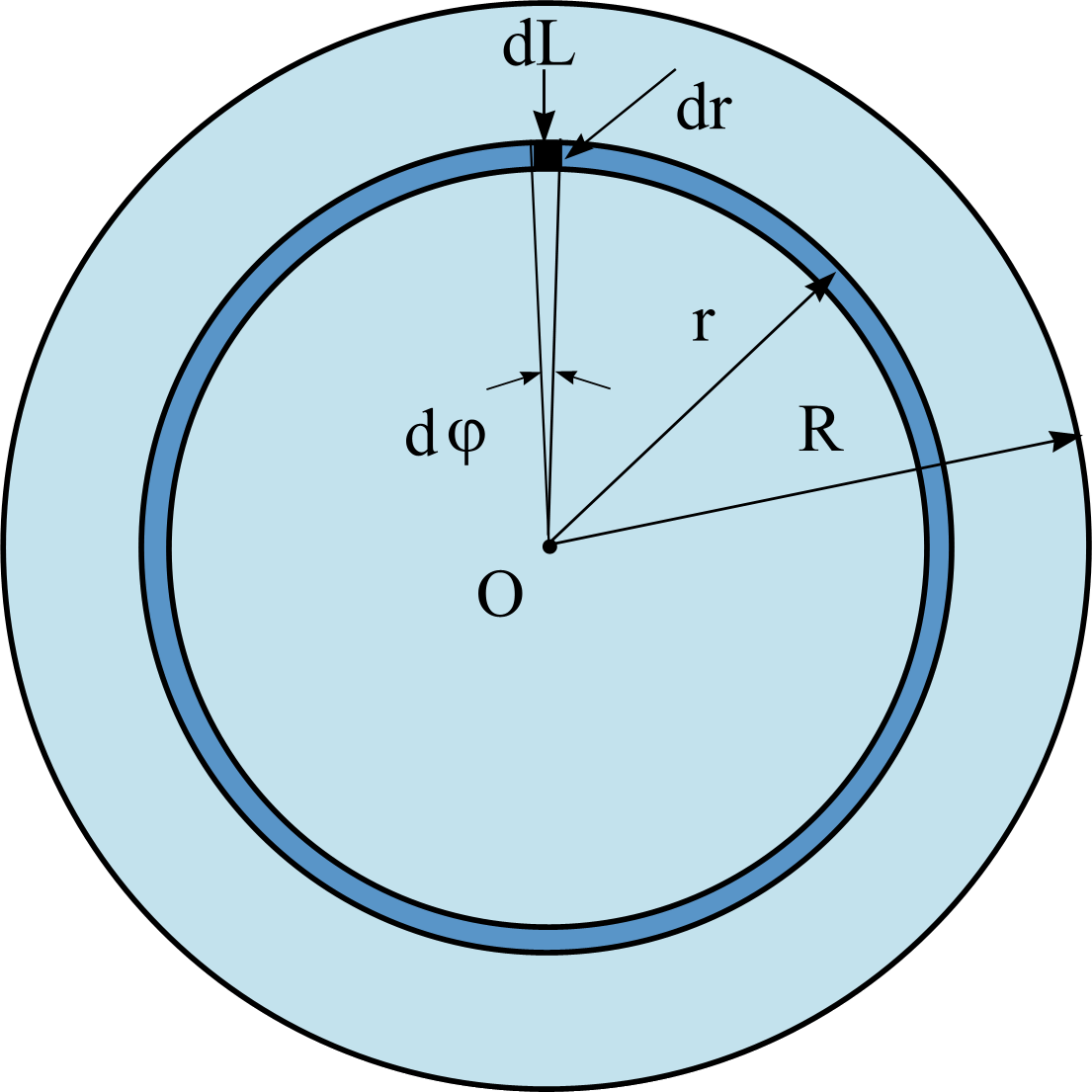
Выделим произвольно элемент диска, отстоящий от его центра на расстоянии r (см. рисунок), и найдем массу dm этого элемента. Для этого нам надо определить выражения для поверхностной плотности материала диска и для площади выделенного элемента.

Поверхностная плотность материала диска равна , где S – площадь поверхности диска. Поскольку S = πR², то поверхностная плотность материала диска равна .

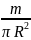Теперь найдем площадь выделенного элемента. При бесконечно малых размерах элемента его площадь dS равна площади прямоугольника со сторонами dL и dr, то есть dS = dL dr. Так как dL = r dφ, то dS = r dr dφ.

Масса выделенного элемента равна произведению поверхностной плотности на его площадь, то есть

dm = ds или dm = r dr dφ.

Момент инерции dJ этого элемента относительно выбранной оси

dJ = dm r² = r³ dr dφ.

Чтобы найти момент инерции всего диска, следует просуммировать момент инерции выделенного элемента по всему диску, для чего надо взять интеграл как по кольцу, элементарной частью которого и является данный элемент, (в пределах от 0 до 2π), так и по радиусу диска (в пределах от 0 до R). Таким образом, как и в предыдущей задаче, нам приходится брать двойной интеграл.

J = 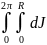или

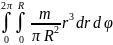J = или J = .

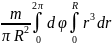Поскольку

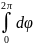= 2π,

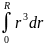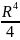= , то

J = 2π = mR².

Ответ: J = mR².

Задача 6. Вычислить момент инерции J однородного сплошного круглого цилиндра относительно продольной оси, проходящей через центры его оснований. R и m – радиус цилиндра и его масса соответственно.

Дано: R, m.

J – ?

Решение.

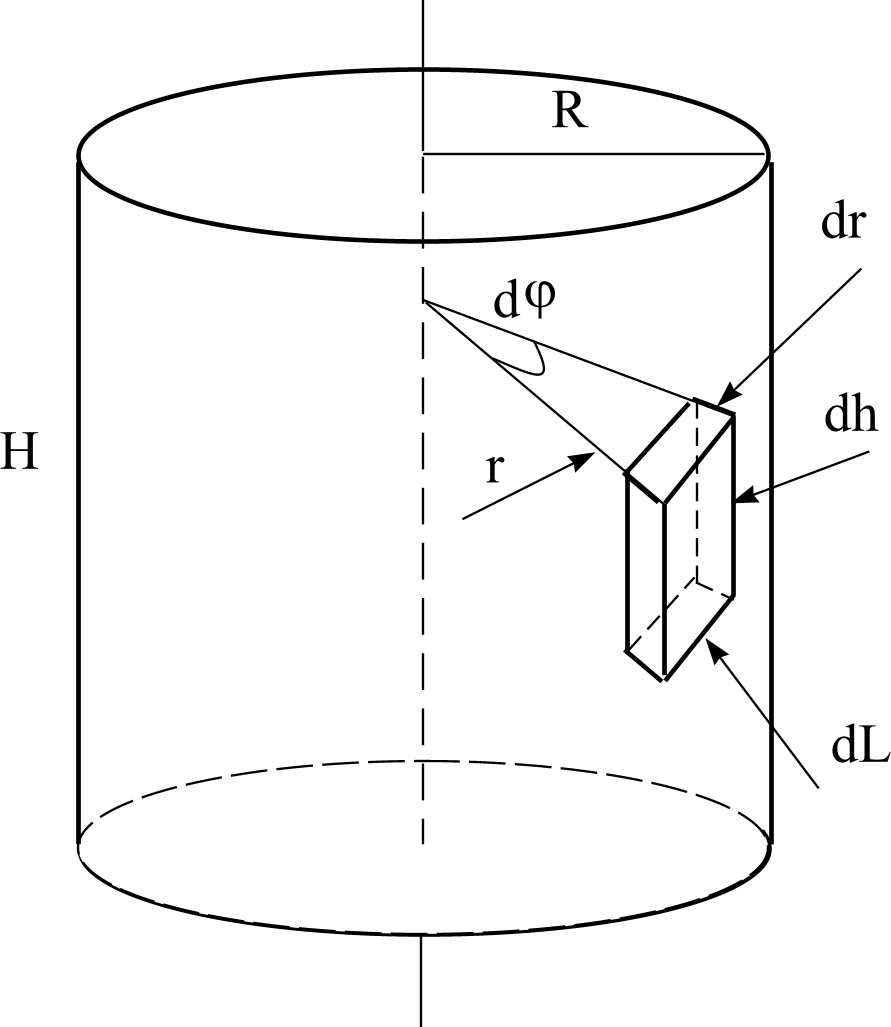
Выделим в теле цилиндра на произвольном расстоянии r от его оси элементарную часть, которая представляет собой параллелепипед высотой dh. Основания параллелепипеда имеют стороны dr и da (см. рисунок). Элементарный объем этого кусочка цилиндра dv = dr dL dh.

Масса единицы объема цилиндра равна = 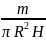, где V = πR²H – объем всего цилиндра (H – высота цилиндра). Это – так называемая объемная плотность цилиндра. Следует знать, что, когда речь идет об объемной плотности тела, то обычно слово «объемная» опускают и говорят просто – плотность.

Чтобы найти массу любого элемента цилиндра, надо его плотность умножить на объем этого элемента. В частности, масса dm выделенного элемента будет равна dm = dv или dm = dr dL dh. Момент инерции выделенного кусочка

dJ = dm r² = dr dL dh r².

Поскольку dL = 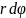, то dJ = dr 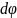dh r³.

Чтобы найти момент инерции всего цилиндра относительно данной оси, надо просуммировать момент инерции выделенного элемента по всему цилиндру. А для этого надо взять интеграл от последнего выражения по радиусу цилиндра (в пределах от 0 до R), по кольцу (в пределах от 0 до 2π), и по высоте (в пределах от 0 до H). Записывается это так:

J =

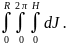
Таким образом, в данном случае нам приходится брать уже тройной интеграл. Процесс вычисления тройного интеграла в принципе ничем не отличается от вычисления двойного интеграла. Постоянные величины выносим за знаки интегралов.

J = 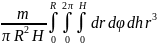или

J = .

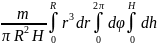Все три интеграла табличные.

= ,

= 2π,

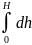= H.

Тогда

J = H = mR².

Ответ: J = mR².

Задача 7. Вычислить момент инерции J однородного кольца массы m относительно оси, проходящей через центр кольца перпендикулярно его плоскости. r₁ и r₂ – внутренний и внешний радиусы кольца соответственно. Толщиной кольца пренебречь.

Дано: m, r₁, r₂.

J – ?

Решение.

Выделим в теле кольца на произвольном расстоянии r от его центра элементарную часть (см. рисунок) и найдем ее массу dm.

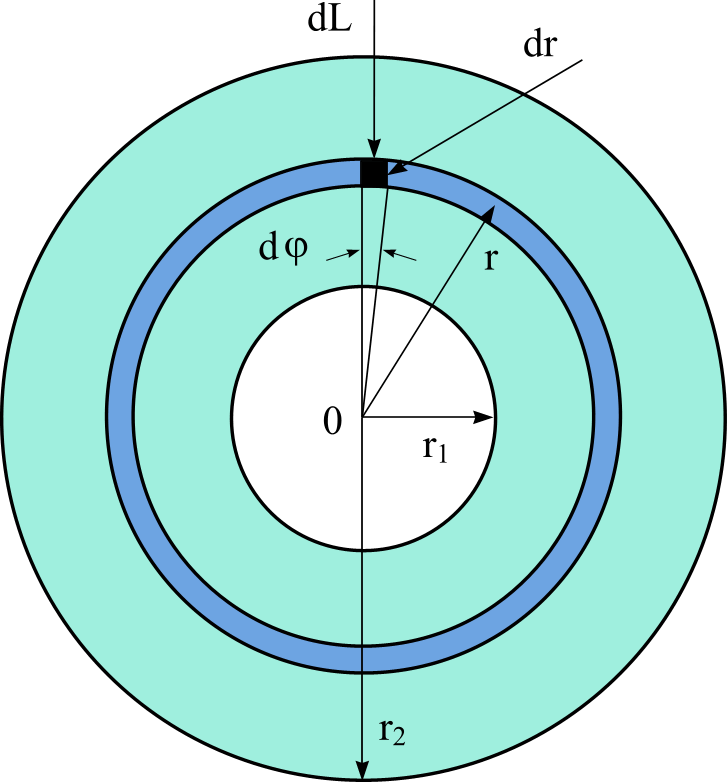
Для нахождения этой массы следует поверхностную плотность кольца умножить на площадь выделенной элементарной части. Чтобы найти поверхностную плотность, нужно массу кольца разделить на его площадь S. Очевидно, площадь кольца равна разности площади круга радиуса r₂ и площади круга радиуса r₁, то есть

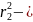S = π 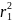π = π(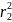 ). Таким образом, поверхностная плотность равна

= .

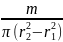Теперь найдем площадь выделенного элемента. При бесконечно малых размерах элемента его площадь dS равна площади прямоугольника со сторонами dL и dr, то есть dS = dL dr. Так как dL = r dφ, то dS = r dr dφ.

Тогда масса выделенного элемента равна dm = r dr dφ.

Момент инерции dJ этого элемента относительно выбранной оси

dJ = dm r² = r³ dr dφ.

Чтобы найти момент инерции всего кольца, следует просуммировать момент инерции выделенного элемента по всему кольцу. Для этого надо взять интеграл как по элементарному кольцу, частью которого и является выделенный элемент (в пределах от 0 до 2π), так и по радиусу (в пределах от r₁ до r₂).

Таким образом,

J = 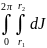или

J =

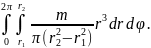
Выносим постоянные величины за знаки интегралов.

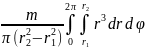J = или J = .

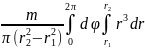Поскольку

= 2π,

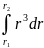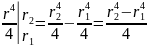= . Тогда

J = 2π = = .

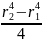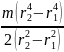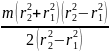Окончательно J = .

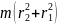Ответ: J = J =

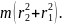
Задача 8. Вычислить момент инерции J однородного полого круглого цилиндра (трубы) массы m относительно оси, проходящей через центры его оснований. r₁ и r₂ – внутренний и внешний радиусы цилиндра соответственно.

Дано: m, r₁, r₂.

J – ?

Решение.

Задача похожа на ту, где мы находили момент инерции сплошного цилиндра, только здесь объем трубы V = π( )Н (Н – высота трубы). Тогда плотность материала трубы равна = 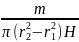. Стало быть, масса dm выделенного элемента

dm = dv, где dv – объем выделенного кусочка. Поскольку

dv = dr dL dh, то dm = dr dL dh. В свою очередь dL = r dφ, тогда

dm = dr r dφ dh.

На рисунке этот элемент не показан, мы его уже показывали на рисунке к задаче 13.2.6.

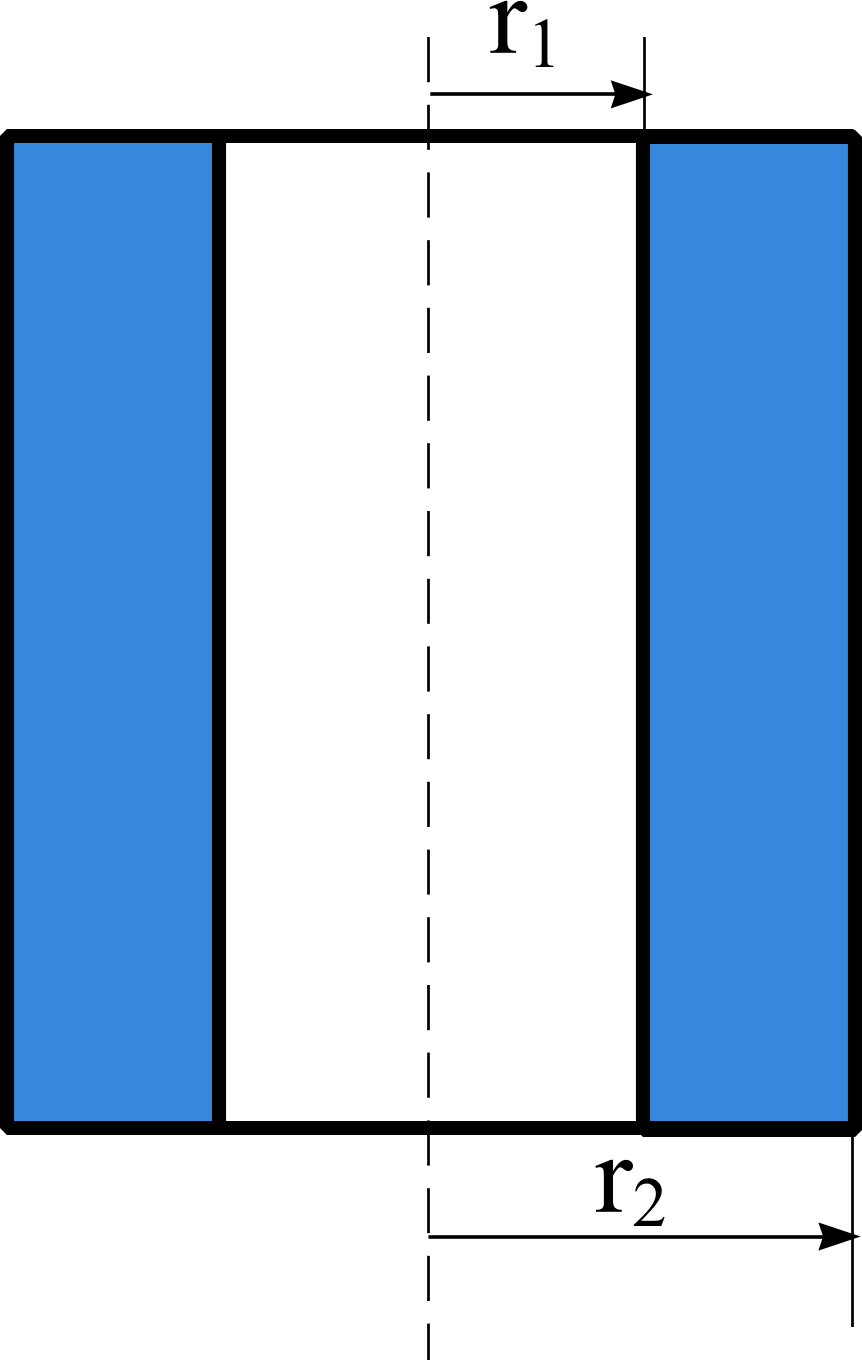
Момент инерции выделенного кусочка трубы

dJ = dm r² = dr r³ dφ dh.

При вычислении момента инерции всей трубы необходимо учесть, что интегрирование выполняется не в пределах от 0 до R, как было в случае сплошного цилиндра, а от r₁ до r₂. Тогда

J = 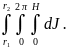Или

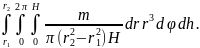J = Выносим постоянные величины за знаки интегралов.

J = 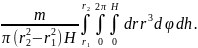Иначе

J = .

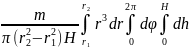Все три интеграла табличные.

= ,

= 2π,

= H.

Тогда

J = 2π H = = .

Окончательно J = .

Ответ: J = J =

Задача 9. Однородный цилиндр массы m совершает плоско-параллельное движение без проскальзывания по неподвижной горизонтальной плоскости. Величина скорости центра масс цилиндра в системе отсчета, связанной с плоскостью, равна v_c. Определить кинетическую энергию цилиндра в этой неподвижной системе отсчета, если поступательно движущаяся его мгновенная ось вращения совпадает: 1) с центральной осью С цилиндра; 2) с осью О₁ касания поверхности цилиндра с плоскостью качения; 3) с осью О₂, перпендикулярной основаниям цилиндра и проходящей через его верхнюю точку.

Дано: m, v_c.

T₁ – ? T₂ – ? T₃ – ?

Решение.

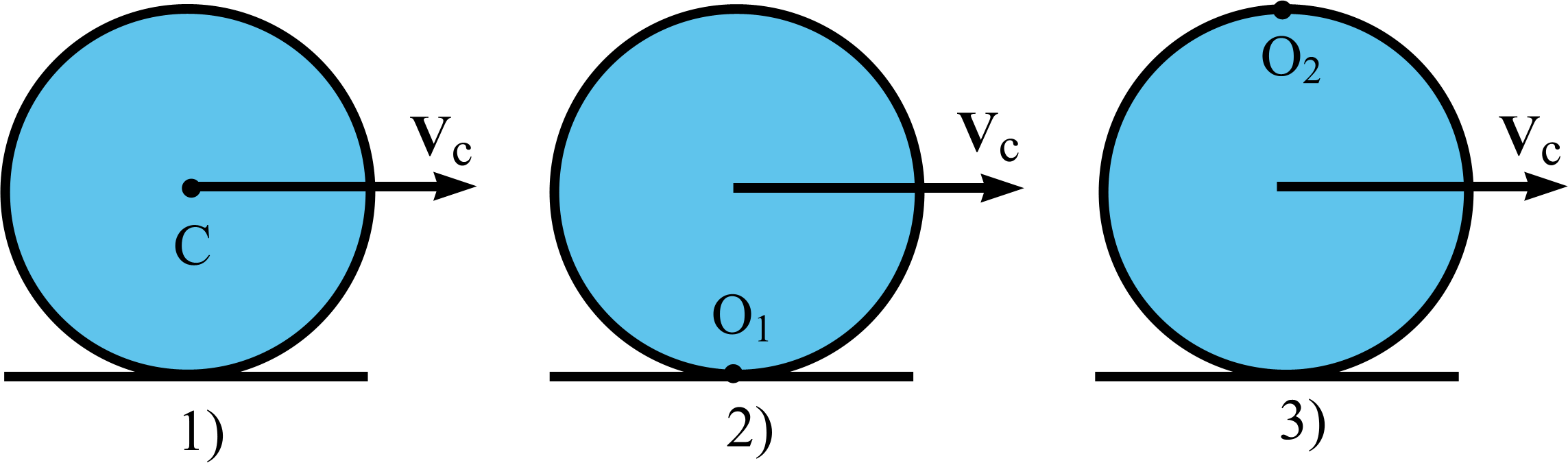
Движение цилиндра представляем как сложное движение, состоящее из совокупности его вращения вокруг оси, проходящей через произвольно выбранную точку, которая называется полюсом, и поступательного движения вместе с системой координат, связанной с полюсом. При этом угловая скорость вращения вокруг выбранной оси (мгновенной оси вращения) не зависит от выбора полюса. Скорость же поступательного движения зависит от выбора полюса.

В общем случае, при произвольном выборе полюса О, кинетическая энергия тела в неподвижной системе отсчета при его плоско-параллельном движении рассчитывается по формуле

Т = +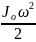 + mv_o v_co, где

m – масса тела,

v_о – скорость поступательного движения тела вместе с выбранным полюсом в неподвижной системе отсчета, связанной с плоскостью качения,

J_о – момент инерции тела относительно оси вращения, проходящей через выбранный полюс,

ω – величина угловой скорости вращения тела,

v_со – скорость центра масс тела в системе отсчета, движущейся поступательно вместе с полюсом О.

1). В данном случае центр масс совпадает с выбранным полюсом, поэтому

v_со = 0, v_о = v_с, J_о = J_с. Следовательно, формула для подсчета кинетической энергии Т₁ принимает простой вид:

Т₁ = + .

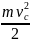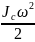Момент инерции цилиндра относительно данной оси, как известно, равен

J_с = 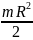(R – радиус цилиндра).

Учитывая, что ω = 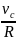, после элементарных преобразований получим

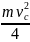Т₁ = + . Или Т₁ = 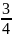m .

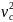2). В этом случае скорость любой точки (в том числе и полюса) данной мгновенной оси вращения О₁ равна нулю. Действительно, эта скорость, определенная по отношению к неподвижной системе отсчета, является абсолютной скоростью, поэтому

v_о = 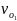+ v_с, где

– скорость любой точки данной оси в системе отсчета, движущейся поступательно вместе с осью вращения, проходящей через центр масс цилиндра (это – относительная скорость), а v_с – это переносная скорость. Ранее (см. задачу 11.3.1) было показано, что скорость любой точки поверхности цилиндра равна по величине скорости центра масс, то есть

= v_с. Поскольку для всех точек оси касания поверхности цилиндра с плоскостью качения = – v_с, то v_о = + v_с = 0. Тогда

Т₂ = 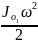, где 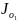– момент инерции цилиндра относительно оси О₁.

Для нахождения воспользуемся теоремой Штейнера.

= J_c + mR² = mR² + mR² = mR².Тогда

Т₂ = m R² ω². Но Rω = v_с, следовательно,

Т₂ = m .

3). Все точки, лежащие на оси вращения О₂, имеют скорость v_о2, направленную так же, как v_с. При этом 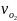= v_с, следовательно, v_о = 2 v_с. Таким образом,

Т₃ = + 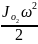+ 2m v .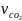

Здесь, – момент инерции цилиндра относительно выбранной оси. Очевидно, как и в предыдущем случае, = mR² (ось О₂ отстоит на таком же расстоянии от центральной оси, как и ось О₁).

Теперь разберемся с . Это – скорость центра масс тела в системе отсчета, движущейся поступательно вместе с осью О₂. По отношению к этой системе отсчета является абсолютной скоростью, а саму систему отсчета считаем условно неподвижной. Система же отсчета, связанная с плоскостью, по которой катится цилиндр, будет, очевидно, перемещаться. Если раньше система отсчета, связанная с осью О₂, перемещалась в направлении поступательного движения цилиндра со скоростью = 2 v_с, в неподвижной системе отсчета, связанной с плоскостью качения, то теперь уже сама эта плоскость перемещается в противоположную сторону с относительной скоростью – 2 v_с. Скорость v_с центра масс цилиндра была раньше абсолютной скоростью в неподвижной системе отсчета, связанной с плоскостью качения цилиндра. Теперь же в новой неподвижной системе отсчета, связанной с осью О₂, она становится переносной скоростью, направленной в ту же сторону, что и раньше. В соответствии с законом сложения скоростей абсолютная скорость центра масс в неподвижной системе отсчета, связанной с осью О₂, (то есть скорость ) равна

= – 2v_с + v_с = – v_с.

Тогда скалярное произведение v_с , входящее в формулу для подсчета Т₃, будет равно:

v_с = – v_с v_с.

Поскольку скалярное произведение вектора самого на себя есть квадрат его модуля, то есть v_с v_с = , то v_с = – . Тогда

Т₃ = 2m + – 2m . Или Т₃ = mR² ω².

Учитывая, что Rω = v_с, окончательно имеем

Т₃ = m .

Во всех трех случаях мы получили одно и то же выражение для кинетической энергии. Так и должно быть: ведь мы рассматриваем кинетическую энергию в одной и той же системе отсчета, просто по-разному описывали движение цилиндра.

Ответ: Т₁ = Т₂ = Т₃ = m .

Задача 10. Каток, представляющий собой однородный круглый цилиндр массы m₁, лежит на горизонтальной плоскости. Каток обмотан тросом, перекинутым через блок, представляющий собой круглый однородный цилиндр массы m₂, вращающийся вокруг неподвижной оси, совпадающей с его осью симметрии. К свободному концу троса прикреплен груз массы m₃. При опускании груза с постоянной скоростью, величина которой равна v, трос, разматываясь, приводит в качение без проскальзывания каток. Определить кинетическую энергию системы каток – блок – груз. Трос считать невесомым и нерастяжимым. Верхние точки катка и блока находятся на одной высоте.

Дано: m₁, m₂, m₃, v.

T – ?

Решение.

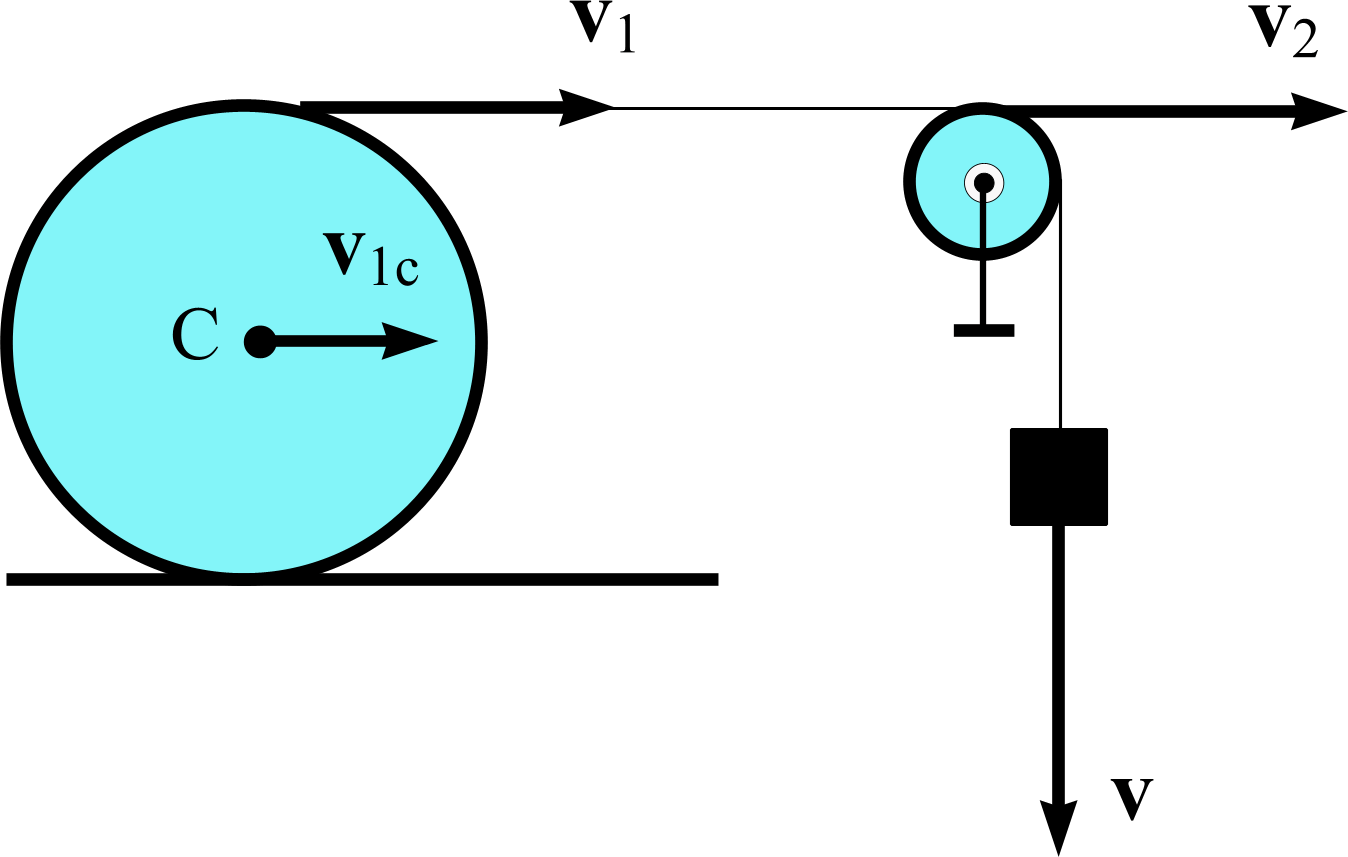
Кинетическая энергия Т системы складывается из кинетических энергий элементов системы, поэтому

Т = Т₁ + Т₂ + Т₃, где Т₁, Т₂, Т₃ – кинетические энергии катка, блока и груза соответственно.

Каток участвует в плоскопараллельном движении, его кинетическая энергия

Т₁ = 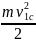+ 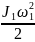, где

v_1с – величина скорости центра масс катка,

J₁ – момент инерции катка относительно его оси симметрии,

ω₁ – величина угловой скорости катка при его вращении вокруг оси симметрии.

Выразим эти величины через данные условия задачи. Очевидно, величина v₁ вектора скорости верхней части катка равна v. Тогда величина скорости центра масс катка v_1c = 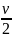. Момент инерции J₁ = m₁ 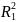, где R₁ – радиус катка. Величина угловой скорости катка ω₁ = 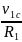= 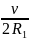. Тогда

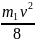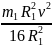Т₁ = + или Т₁ = .

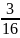
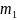
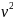Блок вращается вокруг неподвижной оси. Его кинетическая энергия

Т₂ = 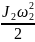, где

J₂ – момент инерции блока относительно его оси вращения.

J₂ = m₂ r², где r – радиус блока.

Поскольку величина v₂ вектора скорости верхней точки блока равна v (считаем, что скольжение между тросом и поверхностью блока отсутствует), то величина его угловой скорости ω₂ = 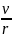. Тогда

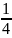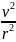Т₂ = m₂ r² = m₂v².

Груз движется поступательно. Его кинетическая энергия

Т₃ = m₃v².

Кинетическая энергия системы

Т = 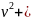m₂v² + m₃v².

Задача решена. Однако ответ можно представить и в ином виде. Вынесем за скобки. Тогда

Т = v² .

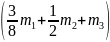Обозначим как М_пр. Тогда

Т = М_пр v². Параметр М_пр – это так называемая приведенная масса системы.

Ответ: Т = М_пр v², где М_пр = .

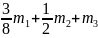Задача 11. В системе, рассмотренной в предыдущей задаче, груз под действием силы тяжести опускается вниз из состояния покоя. Определить величину скорости v груза при опускании его на расстояние h. Трением на оси блока пренебречь.

Дано: m₁, m₂, m₃, h.

v – ?

Решение.

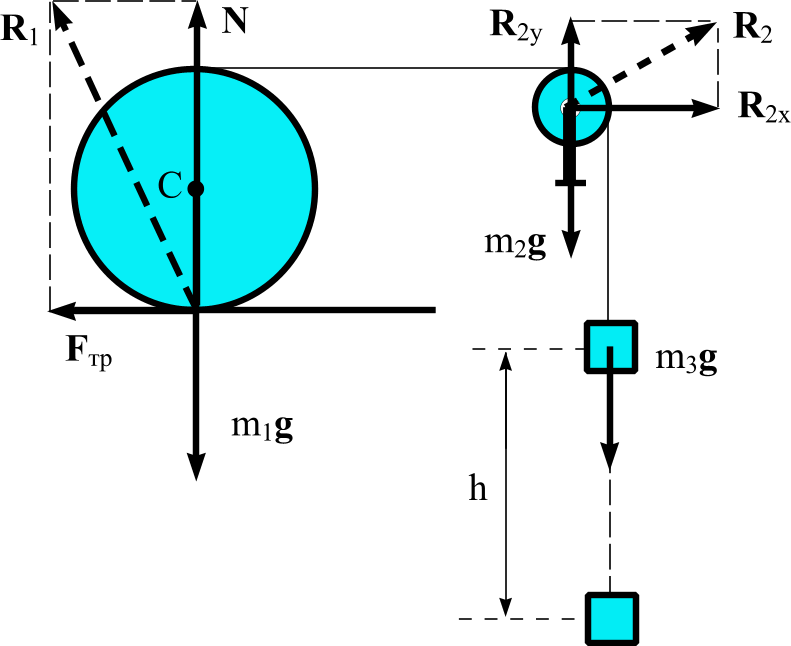
Воспользуемся законом об изменении кинетической энергии системы. Рассмотрим систему в двух состояниях: в момент начала движения груза и в момент, когда груз прошел расстояние h (см. рисунок).

Пусть Т₀ – кинетическая энергия системы в первом состоянии, Т – кинетическая энергия системы во втором состоянии. Тогда

Т – Т₀ = А^(е), где А^(е) – алгебраическая сумма работ всех внешних сил, действующих на систему. Работой внутренних сил системы пренебрегаем, поскольку неконсервативных сил в системе нет. Так как Т₀ = 0 (движение начинается из состояния покоя), то Т = А^(е).

Рассмотрим внешние силы, действующие на систему, и определим работу каждой из них на перемещении, равном по величине h. Этими внешними силами являются:

m₃g – сила тяжести груза. Работа этой силы равна m₃g h,

m₂g – сила тяжести блока. Работа этой силы равна нулю, так как точка приложения этой силы неподвижна,

R₂ – сила реакции, действующая на блок со стороны опоры. Поскольку заранее направление этой силы нам неизвестно, мы представляем ее в виде двух составляющих: R_2х – по горизонтальной оси и R_2у – по вертикальной оси. Работа этой силы реакции равна нулю, так как точка ее приложения неподвижна,

m₁g – сила тяжести катка. Работа этой силы равна нулю, так как сила перпендикулярна к перемещению точки ее приложения (точки С),

R₁ – сила реакции, действующая на каток со стороны плоскости. Эта сила раскладывается на вертикальную составляющую N (это – сила нормальной реакции плоскости) и горизонтальную составляющую F_тр (это – сила трения). Работа каждой из этих сил равна нулю, так как они приложены в мгновенном центре скоростей катка, а элементарное перемещение этого центра равно нулю.

Таким образом, Т = m₃g h.

Выражение для кинетической энергии системы было получено в результате решения предыдущей задачи, напомню его:

Т = М_пр v², где М_пр =

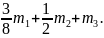
Тогда М_пр v² = m³gh, откуда

v = .

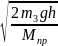Ответ: v = , где М_пр = М_пр =