§ 12.7. Колебательное движение

Задача 1. Найти период колебаний системы, состоящей из двух одинаковых по размеру пружин и твердого тела массой m. Рассмотреть случаи, когда пружины соединены параллельно и последовательно. Жесткости пружин k₁ и k₂ (см. рисунок). Массами пружин пренебречь.

Дано: m, k₁, k₂.

Т₁ − ? Т₂ − ?

Решение.

Известно, что период Т колебаний пружинного маятника определяется выражением:

Т = 2π· , где m – масса тела, закрепленного на свободном конце пружины, k – жесткость пружины.

Вначале рассмотрим маятник с параллельным соединением пружин. Эту систему мы можем мысленно заменить одной пружиной, эквивалентной данной системе, с жесткостью k_пар. В решении задачи 12.4.21 было показано, что жесткость этой эквивалентной пружины равна сумме жесткостей пружин, входящих в систему, то есть k_пар = k₁ + k₂. Тогда период колебаний такого маятника будет определяться формулой:

Т₁ = 2π· = 2π· .

Теперь рассмотрим последовательное соединение пружин. Также мысленно заменим эту систему одной эквивалентной пружиной с жесткостью k_пос. В этом случае k_пос = (см. решение задачи 12.4.21). Тогда период колебаний маятника

Т₂ = 2π· = 2π· .

Ответ: Т₁ = 2π· , Т₂ = 2π· .

Задача 2. Как изменится частота вертикальных колебаний груза, висящего на двух одинаковых пружинах, если от параллельного соединения пружин перейти к их последовательному соединению?

Решение.

Известно, что период Т колебаний пружинного маятника определяется выражением:

Т = 2π· , где m – масса тела, закрепленного на свободном конце пружины, k – жесткость пружины. Поскольку частота f колебаний есть величина, обратная периоду, то

f = .

Из решения предыдущей задачи известно, что при параллельном соединении пружин период Т₁ колебаний находится по формуле:

Т₁ = 2π· , где k₁ и k₂ – жесткости пружин.

Тогда f₁ = .

Аналогично для последовательного соединения пружин

Т₂= 2π· , и

f₂ = .

Если пружины одинаковы, то k₁ = k₂. Пусть k₁ = k₂ = K. Тогда

f₁ = и f₂ = . Следовательно, = 2. Это и есть ответ задачи.

Задача 3. К неподвижной горизонтальной стойке прикреплена вертикально пружина, к нижнему концу которой подвешен груз. В статическом состоянии (пружина с грузом не колеблются) длина пружины оказывается больше первоначальной (то есть той, которую пружина имела без груза) на величину ∆L. Определить период Т гармонических колебаний данного пружинного маятника.

Дано: ∆L.

Т − ?

Решение.

Если к нижнему концу подвешенной вертикально пружине прикрепить груз массой m, то в состоянии равновесия пружина окажется растянутой на величину ∆L по сравнению со своей первоначальной длиной (см. рисунок).

При этом в пружине возникнет упругая сила F, которая по отношению к телу будет являться силой реакции. Величина этой силы F = k ∆L, где k – жесткость пружины. Очевидно, что в состоянии равновесия F = mg или k ∆L = mg, откуда = .

Известно, что период колебаний пружинного маятника с грузом массой m определяется выражением:

Т = 2π· . Подставив сюда найденное выражение для , получим:

Т = 2π· .

Ответ: Т = 2π· .

Задача 4. На вертикальной пружине подвешен грузик. Период колебаний системы Т₁ = 0,5 с. Затем массу грузика увеличивают, в результате чего период колебаний системы становится Т₂ = 0,6 с. Определить на какую величину ∆L удлинилась пружина в состоянии равновесия после увеличения массы грузика.

Дано: Т₁ = 0,5 с, Т₂ = 0,6 с.

∆L − ?

Решение.

Если к нижнему концу подвешенной вертикально пружине прикрепить грузик массой m₁, то в состоянии равновесия пружина окажется растянутой на величину ∆L₁ по сравнению со своей первоначальной длиной. При этом в пружине возникнет упругая сила F₁, которая по отношению к телу будет являться силой реакции. Величина этой силы F₁ = k ∆L₁, где k – жесткость пружины. Очевидно, что в состоянии равновесия F₁ = m₁g или k ∆L₁ = m₁g, откуда величина деформации ∆L₁ = .

Если массу грузика увеличить на m₂, то его общая масса станет m₁ + m₂. В этом случае в пружине возникнет упругая сила F₂, величина которой F₂ = k ∆L₂, где ∆L₂ – деформация пружины в состоянии равновесия по сравнению с ее первоначальной длиной. Очевидно, что в состоянии равновесия F₂ = (m₁ + m₂)g или k ∆L₂ = (m₁ + m₂) g, откуда ∆L₂ = .

Из рисунка видно, что искомая величина ∆L = ∆L₂ − ∆L₁. Тогда

∆L = − или

∆L = 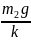. (1)

Однако кроме g ничего больше нам не известно. Поэтому обратимся к другим данным условия задачи.

Период колебаний пружинного маятника с грузиком массой m₁:

Т₁ = 2π· . Или = 4π² .

Аналогично для маятника с грузиком массой m₁ + m₂:

Т₂ = 2π· . Или = 4π² + 4π² .

Тогда − = 4π² , откуда = .

Подставив это выражение в формулу (1), получим:

∆L = g. С учетом числовых значений ∆L = 2,8·10⁻² м или ∆L = 2,8 см.

Ответ: ∆L = 2,8 см.

Задача 5. На идеально гладкой поверхности между двумя неподвижными стенками покоится груз, растянутый пружинами с разными жесткостями. Если груз отклонить в сторону вдоль оси пружин (по перпендикуляру к стенкам), то он начнет колебаться с каким-то периодом. Изменится ли период колебаний, если изменить расстояние между стенками?

Решение.

Когда груз находится между растянутыми пружинами, то на него по горизонтали действуют две силы (см. рисунок): F₁ – сила реакции со стороны левой пружины и F₂ – сила реакции со стороны правой пружины. Величина первой силы

F₁ = k₁ ∆L₁, а величина второй силы F₂ = k₂ ∆L₂, где k₁ и k₂ – жесткости левой и правой пружин соответственно, ∆L₁ – деформация левой растянутой пружины, когда груз находится в равновесии (L₀₁ – первоначальная длина левой пружины), ∆L₂ – деформация правой растянутой пружины при том же условии (L₀₂ – первоначальная длина правой пружины). Деформация (как ∆L₁, так и ∆L₂) это – положительный скаляр, равный расстоянию, пройденному незакрепленным концом пружины при изменении ее размера.

Поскольку груз находится в равновесии, то F₁ + F₂ = 0. После проектирования на ось Х и нахождения проекций, имеем:

F₁ − F₂ = 0 или

k₁ ∆L₁ − k₂ ∆L₂ = 0. (1)

Если теперь груз сдвинуть на небольшую величину х от положения равновесия, например, влево, то деформация левой пружины уменьшится и станет равной

∆L₁ – х, а деформация правой пружины увеличится и будет ∆L₂ + х. При этом величина силы реакции со стороны левой пружины примет значение k₁ (∆L₁ – х), то есть уменьшится по сравнению с тем значением, которое она имела при равновесии. Величина же силы реакции со стороны правой пружины, наоборот, возрастет и станет равной k₂ (∆L₂ + х). Разность этих сил уже не будет равна нулю. Второй закон Ньютона в этом случае будет выглядеть так:

k₁ (∆L₁ – х) − k₂ (∆L₂ + х) = ma_x, где m – масса тела, a_x – проекция ускорения груза на ось Х. Раскрывая скобки и учитывая (1), получим:

(k₁ + k₂) х = ma_х. (2)

Если, после того, как груз был смещен на величину х, его отпустить, то груз будет совершать колебательное движение.

Уравнение (2) – это уравнение колебательного движения груза. Две пружины, входящие в данный пружинный маятник, с жесткостями k₁ и k₂, можно мысленно заменить одной пружиной с жесткостью K = k₁ + k₂. Эта пружина будет эквивалентна двум данным, то есть с этой эквивалентной пружиной колебания маятника будут точно такими же, как и с двумя реальными пружинами. Период колебаний маятника Т = 2π· = 2π· , где m – масса груза.

Мы рассмотрели колебания маятника при каком-то конкретном расстоянии между стенками. Теперь изменим это расстояние, сделаем его тоже каким-то конкретным, но уже не таким, как раньше. Посмотрим, как будет выглядеть уравнение движения груза в этом случае.

Пусть расстояние между стенками стало больше (стенки раздвинули). В этом случае деформации пружин увеличились. Деформация левой пружины в состоянии равновесия стала , а деформация правой пружины приняла значение .

Так же, как и раньше при равновесии k₁ − k₂ = 0.

Также сдвигаем груз на небольшую величину х влево от положения равновесия. После этого, повторяя предыдущие рассуждения, вновь получим:

(k₁ + k₂) х = ma_х.

Таким образом, несмотря на то, что расстояние между стенками стало иным, уравнение движения груза осталось прежним, то есть он будет колебаться с тем же периодом, что и раньше.

Легко показать, что к такому же результату мы придем, если уменьшим расстояние между стенками.

Таким образом, изменение расстояния между стенками не оказывает влияния на период колебаний данного пружинного маятника.

Задача 6. Частица массой m = 0,01 кг совершает гармонические колебания с периодом Т = 2 с. Полная механическая энергия колеблющейся частицы Е = 0,1 мДж. Определить амплитуду А колебаний и наибольшее значение величины F_max силы, действующей на частицу.

Дано: m = 0,01 кг, Т = 2 с, Е = 0,1 мДж.

А − ? F_max − ?

Решение.

Для определения амплитуды колебаний воспользуемся выражением для полной механической энергии колеблющейся частицы:

Е = m ω² A², где ω = − циклическая частота колебаний. Тогда

Е = m A², откуда А = . Подставив числа, получим А = 0,045 м.

Так как частица совершает гармонические колебания, то сила, действующая на нее, является квазиупругой с модулем F = k | x |, где коэффициент пропорциональности k = m ω² = m , x – смещение колеблющейся точки от положения равновесия. Своего максимального значения F_max величина квазиупругой силы достигнет при максимальном значении величины смещения, которое равно амплитуде А колебаний. Таким образом F_max = k А или

F_max = k = m . Окончательно F_max = .

C учетом числовых значений F_max = 4,4 mН.

Ответ: А = 0,045 м, F_max = 4,4 mН.

Задача 7. Определить величину Т натяжения нити в произвольный момент t колебаний математического маятника массой m и длиной L, если угол α отклонения нити маятника от вертикали изменяется по закону α = α_max Sin (ωt + φ₀).

Дано: m, L, α = α_max Sin (ωt + φ₀).

Т − ?

Решение.

Запишем второй закон Ньютона для маятника в «естественной» системе отсчета.

m g + Q + F_и = 0, где

mg – сила тяжести, действующая на маятник со стороны Земли, Q – сила реакции нити,

F_и – сила инерции.

В проекциях на нормаль (см. рисунок):

mg_n + Q_n + F_иn = 0.

Находим проекции:

g_n = g Cos (180⁰ – α) = – g Cos α, Q_n = Q, F_иn = – F_и. Тогда

– m g Cos α + Q – F_и = 0, откуда Q = m g Cos α + F_и.

Модуль силы инерции F_и = , где v – величина линейной скорости колеблющейся частицы. Для нахождения v воспользуемся выражением v = L ω, где величина ω угловой скорости (она же является циклической частотой колебаний) определяется выражением:

ω = = α_max ω Cos (ωt + φ₀). Тогда v = L α_max ω Cos (ωt + φ₀) и

F_и = m L α²_max ω² Cos² (ωt + φ₀).

Учитывая выражение для α, данное в условии задачи, а также найденное выражение для модуля силы инерции, найдем Q:

Q = m g Cos [α_max Sin (ωt + φ₀)] + m L α²_max ω² Cos² (ωt + φ₀).

По третьему закону Ньютона Q = T.

Ответ: T = m g Cos [α_max Sin (ωt + φ₀)] + m L α²_max ω² Cos² (ωt + φ₀).

Задача 8. На двух одинаковых цилиндрах А и В лежит однородный стержень параллельно горизонтальной прямой, проходящей через их центры. Как будет двигаться стержень, если цилиндры начнут одновременно вращаться в противоположные стороны? Коэффициент трения между стержнем и каждым из вращающихся цилиндров постоянен и равен μ. Расстояние между центрами цилиндров равно 2L.

Дано: μ, 2L.

Как будет двигаться стержень?

Решение.

Рассмотрим движение стержня в инерциальной системе отсчета, связанной с Землей. Стержень взаимодействует с тремя объектами – Землей и двумя цилиндрами, следовательно, на него действуют три силы:

mg – сила тяжести со стороны Земли,

R_A – сила реакции со стороны цилиндра А,

R_В – сила реакции со стороны цилиндра В.

Как обычно, раскладываем силы реакций на составляющие:

R_A = N_A + F_трА, R_В = N_В + F_трВ, где N_A и N_В – силы нормальных реакций, действующих на стержень со стороны цилиндров А и В соответственно, F_трА и F_трВ – силы трения со стороны этих же цилиндров (см. рисунок).

Обратите внимание на направления сил трения, они направлены в стороны, противоположные относительным скоростям движения стержня. Так, при вращении цилиндра А по ходу часовой стрелки, как показано на рисунке, точки его поверхности, соприкасающиеся со стержнем, движутся вправо, а сам стержень по отношению к этим точкам – влево. Стало быть, F_трА направлена вправо. Аналогично и для цилиндра В, только в этом случае F_трВ оказывается направленной по рисунку влево. Записываем второй закон Ньютона для стержня:

mg + N_A + F_трА + N_В + F_трВ = ma, где а – ускорение, с которым движется стержень.

После проектирования на ось Х (направление оси показано на рисунке) и нахождения проекций сил, получим:

F_трА – F_трВ = ma_х. Поскольку F_трА = μ N_A, а F_трВ = μ N_В, то

μ (N_A – N_В) = ma_х. (*)

Выясним, чему равна разность, стоящая в скобках. Очевидно, что величина силы давления стержня на цилиндр А будет равна величине силы давления стержня на цилиндр В в том случае, если центр тяжести стержня будет находиться строго на середине отрезка, соединяющего центры цилиндров (точка О на рисунке). Соответственно, в этом случае будут равны N_A и N_В. Понятно, что положить таким образом стержень на цилиндры практически невозможно, его центр тяжести всегда окажется смещенным от середины указанного отрезка на какую-то величину. А раз так, то мы и напрягаться не будем, а положим стержень таким образом, чтобы его центр тяжести заведомо был смещен на величину х, например, вправо от точки О. Проследим, однако, чтобы смещение было не таким уж и большим, иначе стержень может просто упасть с цилиндров.

Поскольку стержень не вращается, то сумма моментов всех действующих на стержень сил должна быть равна нулю. Поскольку точка, относительно которой вычисляются моменты, может быть выбрана произвольно, то пусть это будет точка О. Моменты сил трения относительно данной точки равны нулю, поскольку равны нулю плечи этих сил. Следовательно, остаются три силы: mg, N_A и N_B. Обозначим их моменты соответственно как M_g, M_A и M_B. Тогда

M_g + M_A + M_B = 0.

В проекциях на ось Z, проходящую через точку О перпендикулярно плоскости рисунка и направленную от нас

M_gz + M_Az + M_Bz = 0.

После нахождения проекций, получим

M_g + M_A – M_B = 0.

Учитывая, что х – плечо силы mg, L – плечо силы N_A, и L – плечо силы N_В, имеем:

mg x + N_AL – N_ВL = 0, откуда N_A – N_В = – . Тогда выражение (*) принимает вид:

– μ = ma_х.

Итак, мы получили уравнение второго закона Ньютона в проекциях на горизонтальную ось Х. Левая часть уравнения – это проекция на данную ось какой-то силы, определяющей ускорение стержня вдоль этой оси. Понятно, что этой силой является результирующая сил трения, действующих на стержень как со стороны цилиндра А, так и со стороны цилиндра В, поскольку никакие другие силы вдоль оси Х на стержень не действуют. Обозначим эту результирующую силу как F. Тогда F_x = – μ . Иначе, F_x = – kx, где k = μ . Теперь мы можем ответить на вопрос, как движется стержень. Ответ такой: движением стержня являются гармонические колебания, происходящие вдоль оси Х, поскольку величина силы, действующей на стержень вдоль этой оси пропорциональна его смещению, а направление силы противоположно перемещению стержня.

Зная, что коэффициент пропорциональности k = m ω² = m , найдем период Т колебаний стержня: T = 2π . Подставив сюда полученное выше выражение для k, получим T = 2π .

Ответ: стержень совершает гармонические колебания с периодом T = 2π .