§ 12.5. Вращательное движение

Задача 1. Ведро с водой, привязанное к веревке длиной L, равномерно вращается в вертикальной плоскости. Найти величину v_мин наименьшей скорости вращения ведра, при которой в высшей точке вода из него не выливается. Какова величина Т силы натяжения веревки при этой скорости в высшей и низшей точках окружности. Масса воды m. Массой самого ведра пренебречь. Размер ведра много меньше длины веревки.

Дано: L, m.

v_мин − ? Т − ?

Решение.

Решим задачу в системе отсчета, связанной с Землей. Ось Y направим вверх (рисунок 1). В выбранной системе отсчета на воду действуют следующие силы: сила тяжести mg и сила N нормальной реакции дна. Направления этих сил для верхней и нижней точек окружности показаны на рисунке слева.

Рис. 1

Запишем второй закон динамики для воды.

mg + N = m a_цент. или в проекциях на выбранную ось:

mg_y + N_y = ma_цент.y. (1)

Верхняя точка окружности. Здесь g_y = – g, N_y = – N, a_цент.y – это проекция центростремительного (нормального) ускорения a_цент. на ось Y. Мы знаем, что модуль этого ускорения равен . В верхней точке окружности вектор a_цент. и ось Y направлены в противоположные стороны, следовательно, a_цент.y = – . Тогда

mg + N = m . (2)

Что будет происходить с водой, если она в верхней точке траектории начнет выливаться из ведра? Конечно, она просто-напросто начнет перемещаться по вертикали вниз, в сторону Земли. И здесь мы должны учесть одну из особенностей воды (это относится вообще ко всем жидкостям): в отличие от газов и твердых тел жидкость практически несжимаема и нерастяжима.

Чтобы ответить на первый вопрос задачи, надо обязательно иметь в виду эту особенность жидкости. Ведь, как только вода начнет выливаться, то начнут двигаться по направлению к Земле не только те слои воды, которые расположены у открытого края ведра, но и все другие ее слои, то есть придет в движение по направлению к Земле сразу вся вода. А, значит, и те ее участки, которые прилегают к дну ведра. А это, в свою очередь, означает, что, как только вода начнет выливаться, то ее контакт с дном сразу прекратится (между дном и водой возникнет зазор), стало быть, вода перестанет «чувствовать» дно. Другими словами, дно перестанет быть связью, и, следовательно, ни о какой реакции связи уже говорить не приходится. Проще сказать, N = 0.

В этом случае второй закон динамики будет выглядеть так:

mg = m , откуда v_мин = .

Теперь займемся веревкой, точнее, силой, которая веревку натягивает. Откуда вообще эта сила берется? Рассмотрим подробнее этот вопрос, поскольку во многих пособиях, в которых разбирается эта задача, его как-то «проглатывают».

Когда вода касалась дна (еще до того, как она стала выливаться), то дно являлось для воды связью, и, как и положено связи, действовало на воду какой-то силой (мы о ней говорили, это – сила нормальной реакции дна, то есть N). Но нельзя забывать (ох, как часто забывают!), что и вода «в долгу не остается» и в соответствии с третьим законом динамики действует на дно точно с такой же по величине силой. Если сила нормальной реакции N действует на воду со стороны дна, то есть приложена к воде и направлена в этой точке траектории вертикально вниз, то на дно со стороны воды действует сила, которая называется силой нормального давления F_д. Она приложена к дну ведра и направлена в противоположную, чем N сторону, то есть F_д направлена вертикально вверх (все в соответствии с третьим законом). По модулю эти силы равны, то есть F_д = N (рисунок в центре). Поскольку ведро – твердое тело, а веревка жестко соединена с ведром, то эта сила будет приложена и к веревке. Она-то веревку и натягивает. Силу, которая натягивает веревку (нить, трос, стержень…) принято обозначать буквой Т. В нашем случае F_д и T – это одно и то же.

Если же вода вдруг стала выливаться, то, как мы выяснили, дно перестает быть связью, пропадает сила реакции связи, то есть N. Сразу же исчезает F_д (рисунок 1 справа). Значит, и веревка перестает быть натянутой, то есть Т = 0.

Надо заметить, что это справедливо при условии, что масса самого ведра равна нулю (о чем и предупреждено в нашем условии задачи). Вообще-то еще нелишне было бы сказать, что и трением между водой и стенками ведра пренебрегаем…

Нижняя точка окружности. Здесь g_y = – g, N_y = N, a_цент.y = . Тогда

− mg + N = m , откуда N = m . Подставляя сюда найденное ранее выражение для величины скорости, получим:

N = 2mg, следовательно, и величина силы нормального давления F_д на дно ведра со стороны воды, и величина силы натяжения T нити будут равны 2mg.

Задача решена. Теперь посмотрим, как будет выглядеть решение в «естественной» системе отсчета, то есть в системе, вращающейся с таким же центростремительным ускорением, что и ведро с водой.

Рис. 2

Система координат – это ось нормали и касательная ось с ортами n и τ соответственно (рисунок 2). Чем же отличается такая система от предыдущей, и изменится ли решение задачи при переходе к новой системе отсчета?

Отличие, конечно, очень большое. Если первая система была инерциальной, то вторая уже таковой не является: она сама движется с центростремительным ускорением. А это значит, что изучаемое тело в этой системе отсчета не вращается, то есть, даже, если тело в данной системе отсчета и движется, то без центростремительного ускорения. Кроме того, в такой системе отсчета возникает дополнительная сила, так называемая фиктивная сила или сила инерции F_и. По модулю F_и = m | a_цент. |, но направлена в сторону, противоположную центростремительному ускорению, то есть

F_и = − m a_цент..

Как решать задачи в такой системе отсчета? В этом случае мы просто корректируем второй закон динамики: вводим силу инерции и убираем центростремительное ускорение. Тогда вместо уравнения (1) мы будем иметь такое уравнение:

mg + N + F_и = 0. Или

mg + N − m a_цент. = 0.

Правда, имейте в виду, что убирается только нормальное ускорение (оно у нас обозначено как a_цент.), к касательному ускорению это не относится, оно остается. В этом более общем случае уравнение будет выглядеть так:

mg + N + F_и = mа_τ, или mg + N − m a_цент. = mа_τ.

После проектирования на нормаль и нахождения проекций, будем иметь:

mg + N − m = 0 или mg + N = m . (Проекция на нормаль касательного ускорения все-равно равна нулю, даже, если тело и движется с касательным ускорением).

То есть мы пришли к уравнению (2). Таким образом, результат решения задачи будет одним и тем же, независимо от того, в какой системе отсчета было выполнено решение. Какую же систему выбирать? Какую хотите… Главное – разобраться, чем одна система отличается от другой и не путаться. А то, по незнанию, бывает так, что человек краем уха слышал, что какие-то там силы инерции существуют, и добросовестно приплюсовывает силу инерции к другим силам, и тут же в другой части уравнения опять же добросовестно записывает центростремительное ускорение. Вот такая получается «каша».

Ответ: v_мин = . В верхней точки окружности Т = 0. В нижней точке Т = 2mg.

Задача 2. Автомобиль массой m движется по мосту, радиус кривизны которого R. С какой по величине F силой давит автомобиль на мост в точке, направление на которую из центра кривизны моста составляет с вертикалью угол α? С какой по величине F₁ силой давит автомобиль на середину моста? Величина скорости автомобиля в точке, где определяется сила давления, равна v. Решить задачу как для выпуклого моста, так и для вогнутого.

Дано: m, v, R, α.

F − ? F₁ − ?

Решение.

Решение задачи выполним в «естественной» системе отсчета.

Запишем второй закон Ньютона для автомобиля в самом общем виде:

= ma, где левая часть уравнения – это векторная сумма всех действующих на автомобиль сил, а – полное ускорение автомобиля.

Спроектируем это векторное уравнение на нормаль (нам этого будет достаточно).

= ma_n.

Очевидно, что силы, действующие на автомобиль вдоль направления его скорости (вдоль касательной), при проектировании на нормаль дадут нуль, поэтому они нас интересовать не будут. Это такие силы, как, например, сила трения, сила, обеспечивающая вообще движение автомобиля (например, за счет работы двигателя или за счет того, что автомобиль тянут на буксире). Тогда остаются только три силы, которые имеют отличные от нуля проекции на нормаль. Это сила тяжести mg, и сила нормальной реакции N дороги и сила инерции F_и. Только они и будут представлены на рисунках.

Что касается ускорения, то при проектировании останется только проекция нормального ускорения: касательное ускорение, даже, если оно и существует (например, автомобиль разгоняется или, наоборот, тормозит), имеет нулевую проекцию на нормаль. Кроме того, в выбранной «естественной» системе отсчета нормальное ускорение отсутствует, поскольку сама система отсчета вращается вместе с объектом. Тогда второй закон динамики принимает вид: = 0.

Выпуклый мост (рис. 1).

В проекциях на нормаль последнее уравнение запишется так:

mg_n + N_n + F_иn = 0.

Рис. 1

Поскольку mg_n = mg Cos α, N_n = − N, F_иn = – F_и, то mg Cos α – N – F_и = 0. Так как F_и = m , то N = mg Cos α − m .

По третьему закону с такой же по величине силой и автомобиль будет действовать на мост. Таким образом,

F = mg Cos α − m .

На середине моста α = 0. Тогда F₁ = mg − m .

Вогнутый мост (рис. 2).

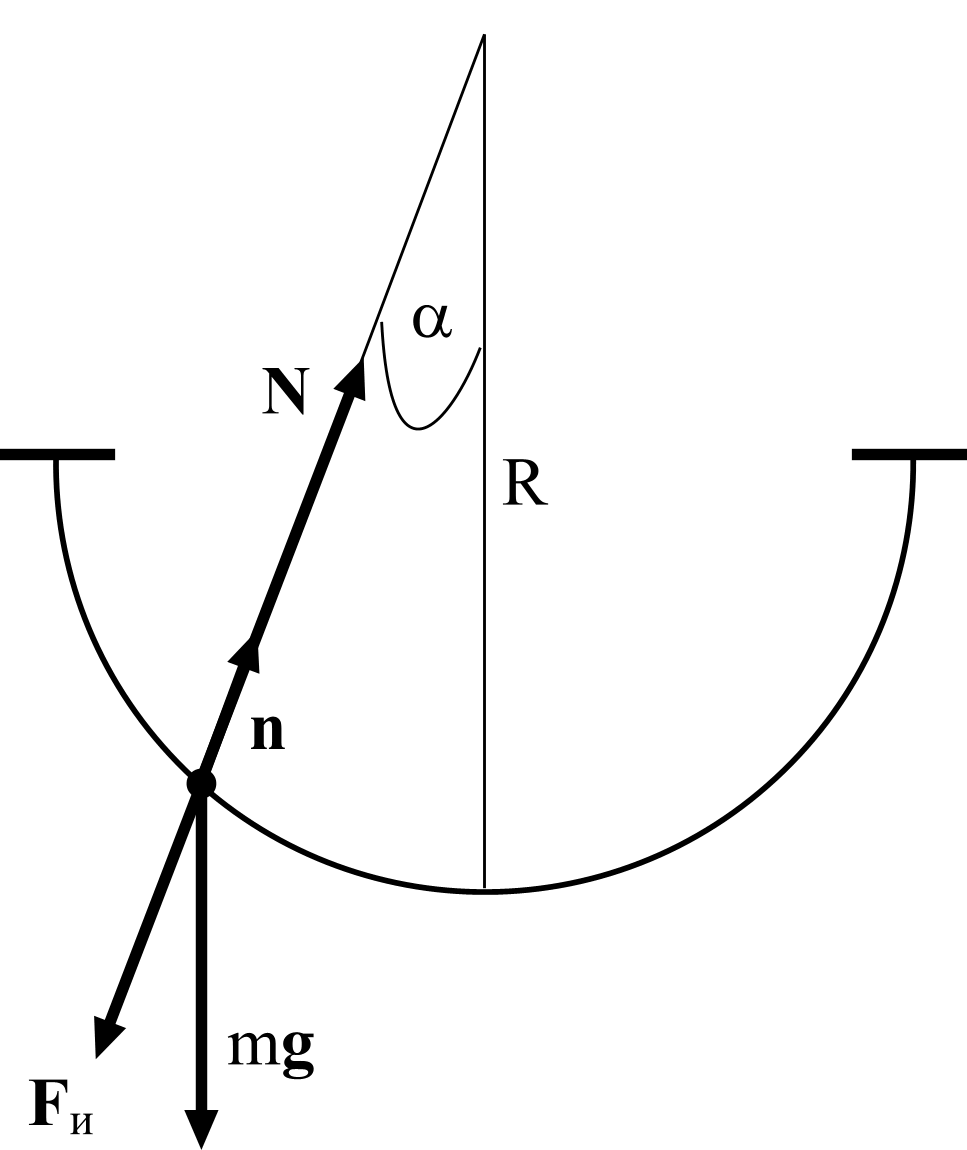
Рис. 2

В этом случае

mg_n = mg Cos (180⁰ – α) = − mg Cos α,

N_n = N, F_иn = − F_и = − m . Тогда

− mg Cos α + N = m , откуда

N = mg Cos α + m .

Следовательно, F = mg Cos α + m .

На середине моста α = 0.

Тогда F₁ = mg + m .

Ответ: Выпуклый мост. F = mg Cos α − m , F₁ = mg − m .

Вогнутый мост. F = mg Cos α + m , F₁ = mg + m .

Задача 3. Груз массой m, подвешенный на тонкой, невесомой и нерастяжимой нити, отклоняют на угол α = 60⁰ и отпускают. Найти величину Т силы натяжения нити в момент прохождения грузом положения равновесия.

Дано: m, α = 60⁰.

Т − ?

Решение.

Решение задачи выполним в «естественной» системе отсчета.

Груз взаимодействует с Землей и нитью, поэтому на него действуют две «правильные» силы (mg – сила тяжести и Q – сила реакции нити) и одна – фиктивная (F_и).

Второй закон динамики для груза:

mg + Q + F_и = 0.

В проекциях на нормаль:

mg_n + Q_n + F_иn = 0. Найдем эти проекции для момента прохождения грузом положения равновесия (см. рисунок). В этом случае g_n = − g, Q_n = Q,

F_иn = – F_иn = – m , где v – величина скорости груза в данный момент времени, L – длина нити. Тогда

Q – mg = , откуда Q = m . Так как по третьему закону динамики

Q = T, то сила натяжения нити

T = m . (1)

Теперь воспользуемся законом сохранения механической энергии консервативной системы груз – Земля (надеюсь, Вы уже сами можете объяснить, почему данная система является консервативной).

Рассмотрим систему в двух состояниях. Первое состояние соответствует моменту, когда груз отклонен от вертикали на угол α. В этом случае груз оказался поднятым на высоту h по отношению к тому положению, в котором груз находился при равновесии. Если считать, что в положении равновесия груз обладал нулевой потенциальной энергией, то в первом положении системы полная механическая энергия груза равна mgh. Причем h = L – L Cos α (см. рисунок). Или h = L (1 – Cos α). Тогда энергия груза в первом состоянии системы U = mgL (1 – Cos α).

Второе состояние системы соответствует моменту прохождения грузом положения равновесия. Механическая энергия груза в этом состоянии

Т = . Так как система консервативна, то U = T или mgL (1 – Cos α) = , откуда v² = 2gL (1 – Cos α). Подставив это выражение в формулу (1), после несложных преобразований получим:

T = mg (3 – 2Cos α). Поскольку Cos 60⁰ = , то T = 2mg.

Ответ: T = 2mg.

Задача 4. Гирька, привязанная к невесомой нерастяжимой нити длиной L = 30 см, описывает в горизонтальной плоскости окружность радиусом R = 15 см. С какой частотой n вращается гирька?

Дано: L = 30 см = 0,3 м, R = 15 см = 0,15 м.

n − ?

Решение.

Решение задачи выполним в инерциальной системе отсчета, связанной с Землей.

Груз взаимодействует с Землей и нитью, поэтому на него действуют две силы: mg – сила тяжести и Q – сила реакции нити. В выбранной системе отсчета никаких сил инерции нет!

Второй закон динамики для груза:

mg + Q = ma.

Спроектируем это векторное уравнение на координатные оси X и Y (см. рисунок).

В проекциях на ось X:

Mg_x + Q_x = ma_x. В этом случае g_x = 0, Q_x = Q Sin α, a_x = , где v – величина скорости груза. Тогда

Q Sin α = (1)

В проекциях на ось Y:

Mg_y + Q_y = ma_y. В этом случае g_y = − g, Q_y = Q Cos α, a_y = . Тогда

Q Cos α = mg. (2).

Делим уравнение (1) на уравнение (2). В результате получим:

tg α = . Поскольку v = Rω = R2πn (ω – угловая скорость гирьки), то

tg α = , откуда n = 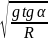. Из рисунка видно, что tg α = . Тогда

n = . Подставив числа, получим n ≈ 1 .

Ответ: n ≈ 1 .

Задача 5. Камень массой m = 0,5 кг, привязанный к невесомой нерастяжимой нити длиной L = 0,5 м, равномерно вращается в вертикальной плоскости. Сила натяжения нити в нижней точке окружности Т = 44 Н. На какую высоту h, считая от нижней точки траектории, поднимется камень, если веревка обрывается в тот момент, когда скорость камня направлена вертикально вверх?

Дано: m = 0,5 кг, L = 0,5 м, Т = 44 Н.

h − ?

Решение.

В нижней точке траектории сила натяжения нити определяется следующим выражением (см. вывод формулы (1) в решении задачи 12.5.3).

T = m . Отсюда v² = L .

Это выражение получено для нижней точки траектории камня, но оно будет справедливо и для любой точки траектории, так как по условию данной задачи камень вращается равномерно, то есть с постоянной по величине скоростью.

Применим для консервативной системы камень – Земля закон сохранения механической энергии, рассматривая систему в двух состояниях: в момент обрыва нити и в момент достижения камнем высоты h. При этом потенциальную энергию камня при обрыве нити положим равной нулю (таково наше условие нормировки). Тогда

m = mgh, откуда h = . С учетом полученного ранее выражения для квадрата скорости, будем иметь:

h = . Подставив числа, получим h = 2 м.

Ответ: h = 2 м.

Задача 6. Гиря массой m = 0,5 кг, привязанная к резиновому шнуру, описывает в горизонтальной плоскости окружность. Частота вращения гири n = 2 . Угол отклонения резинового шнура от вертикали α = 30⁰. Жесткость шнура k = 0,6 . Найти длину L₀ нерастянутого резинового шнура.

Дано: m = 0,5 кг, n = 2 , α = 30⁰, k = 0,6 = 600 , ρ = 10³ .

L₀ − ?

Решение.

Решение задачи выполним в инерциальной системе связанной с Землей.

Гиря взаимодействует с Землей и нитью, поэтому на нее действуют две силы: mg – сила тяжести и Q – сила реакции нити.

Второй закон динамики для гири:

mg + Q = ma.

Спроектируем это векторное уравнение на оси X и Y (см. рисунок).

В проекциях на ось X:

mg_x + Q_x = ma_x. В этом случае g_x = 0, Q_x = Q Sin α, a_x = , где v – величина скорости гири, R – радиус описываемый гирей окружности. Тогда

Q Sin α = (1)

В проекциях на ось Y:

mg_y + Q_y = ma_y. В этом случае g_y = − g, Q_y = Q Cos α, a_y = . Тогда

Q Cos α = mg. (2).

Поскольку Q = k·∆L (∆L – растяжение шнура), Sin α = (L – длина растянутого шнура), v² = ω² R² = 4π²n²R² (ω = 2πn – угловая скорость гири), то уравнения (1) и (2) примут вид:

= 4π² n² m,

k ∆L Cos α = mg.

Имеем систему двух уравнений с двумя неизвестными (L и ∆L).

Решая эту систему, получим:

L = , ∆L = .

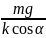Длина нерастянутого шнура L₀ = L − ∆L или

L₀ = . Подставив числа, получим L₀ = 0,06 м.

Ответ: получим L₀ = 0,06 м.

Задача 7. Груз массой m = 0,5 кг, привязанный к резиновому шнуру длиной L₀ = 9,5 см, отклоняют на угол α = 90⁰ и отпускают. Найти длину L резинового шнура в момент прохождения грузом положения равновесия. Жесткость шнура k = 1 .

Дано: m = 0,5 кг, L₀ = 9,5 см = 9,5·10⁻² м, α = 90⁰, k = 1 .

L − ?

Решение.

Задачу решим в неподвижной системе отсчета, связанной с Землей.

На груз действуют: сила тяжести mg и сила реакции шнура Q. Запишем второй закон динамики для груза в проекциях на ось Y (см. рисунок).

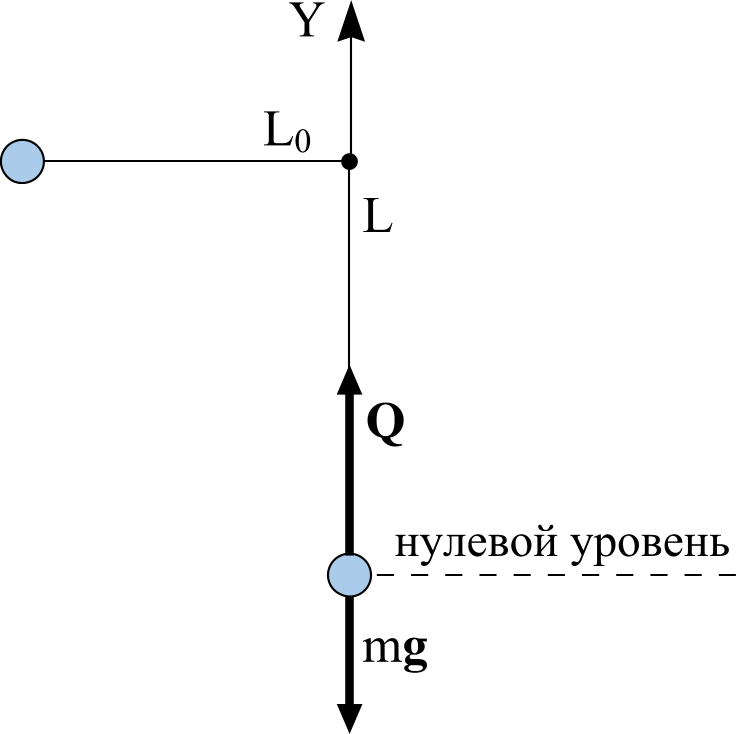
mg_y + Q_y = ma_y. В момент прохождения грузом положения равновесия

g_y = − g, Q_y = Q = k·∆L (∆L = L – L₀ – растяжение шнура), a_y = (v – величина скорости груза в указанный момент). Тогда

k·∆L – mg = . Или

k·(L – L₀) – mg = . (1)

Рассмотрим систему груз – Земля в двух состояниях: в момент, когда α = 90⁰ и в момент, когда груз проходит положение равновесия.

Система не является консервативной, поскольку на нее действует внешняя сила реакции шнура, работа которой не равна нулю. Запишем для данной системы закон изменения механической энергии при переходе системы из первого состояния во второе.

∆T + ∆U = A, где

∆T = – 0 = – изменение кинетической энергии системы,

∆U = 0 – mgL = – mgL − изменение потенциальной энергии системы (в положении равновесия потенциальная энергия системы принята равной нулю),

А = − = − – работа силы реакции шнура при его растяжении. Тогда

– mgL = − . Или

= mgL − . (2)

Таким образом, мы получили систему уравнений (1) и (2) с двумя неизвестными (L и v). Для решения системы изменим форму записи уравнения (1). Для этого обе части уравнения умножим на . В результате получим:

= − . Осталось приравнять правые части последнего уравнения и уравнения (2).

− = mgL − . Выполнив несложные преобразования, получим:

2k L² – 3 (mg + k L₀) L + k = 0.

Теперь подставим числа и решим квадратное уравнение. В результате

L = 0,11 м.

Ответ: L = 0,11 м.

Задача 8. Вокруг горизонтальной оси может без трения вращаться рычаг, плечи которого равны L₁ и L₂. На концах рычага укреплены грузы с массами, равными соответственно m₁ и m₂. Предоставленный самому себе рычаг переходит из горизонтального положения в вертикальное (см. рисунок). Какую по величине скорость v₂ будет иметь в нижней точке груз с массой m₂? Массой самого рычага пренебречь.

Дано: L₁, L₂, m₁, m₂.

v₂ − ?

Решение.

Рассмотрим систему рычаг с грузами – Земля. Система консервативна, поэтому применим к ней закон сохранения механической энергии. Пусть первое состояние системы соответствует нахождению рычага с грузами в горизонтальном положении. Во втором состоянии рычаг с грузами располагается вертикально.

Механическая энергия W₁ системы в первом состоянии складывается из потенциальной энергии U₁ первого груза и потенциальной энергии U₂ второго. Таким образом, полная энергия в этом случае W₁ = U₁ + U₂. Потенциальную энергию системы будем отсчитывать от уровня самого нижнего положения второго груза. Тогда U₁ = m₁gL₂, U₂ = m₂gL₂, W₁ = m₁gL₂ + m₂gL₂.

Механическая энергия W₂ системы во втором состоянии складывается из потенциальной энергии U′₁ и кинетической энергии Т′₁ первого груза, а также из кинетической энергии Т′₂ второго (потенциальная энергия второго груза в соответствии с нашим условием нормировки равна нулю).

Таким образом, полная энергия в этом случае W₂ = U′₁ + Т′₁ + Т′₂. Поскольку

U′₁ = m₁g (L₁ + L₂), Т′₁ = , Т′₂ = , то W₂ = m₁g (L₁ + L₂) + + , где v₁ и v₂ – величины скоростей первого и второго груза соответственно во втором состоянии системы.

Как в первом, так и во втором состояниях системы не учитывалась механическая энергия самого рычага, так как его массой мы пренебрегаем.

Поскольку система консервативна, то W₁ = W₂, то есть

m₁gL₂ + m₂gL₂ = m₁g (L₁ + L₂) + + . (1)

В этом уравнении две неизвестные величины: v₁ и v₂, поэтому необходимо еще одно уравнение, куда входили бы эти неизвестные. Это второе уравнение получим, исходя из того, что все точки рычага имеют одинаковую угловую скорость. Величина угловой скорости точки рычага, где находится груз с массой m_1, равна ω₁ = . Для точки нахождения груза с массой m₂ величина угловой скорости ω₂ = . Итак, ω₁ = ω₂ или

= . (2)

Таким образом, мы имеем систему двух уравнений (1) и (2) с двумя неизвестными v₁ и v₂. Решим ее.

Раскрыв скобки и, сделав несложные преобразования в уравнении (1), получим:

m₁ + m₂ = 2g (m₂L₂ – m₁L₁). (3)

Из уравнения (2) выразим v₁ и возведем в квадрат. Получим: = . Подставим это выражение в уравнение (3), и после простых преобразований будем иметь:

v₂ = L₂ . Это выражение и является ответом задачи.

Задача 9. Шарик массы m, висящий на тонкой нерастяжимой нити длины L, отводят в сторону так, что нить занимает горизонтальное положение, и отпускают без толчка. Внизу на расстоянии h = L под точкой подвеса вбит гвоздь. Какова величина Т силы натяжения нити в момент, когда меньшая часть нити займет горизонтальное положение? Массой нити и трением пренебречь.

Дано: m, L, h = L.

Т − ?

Решение.

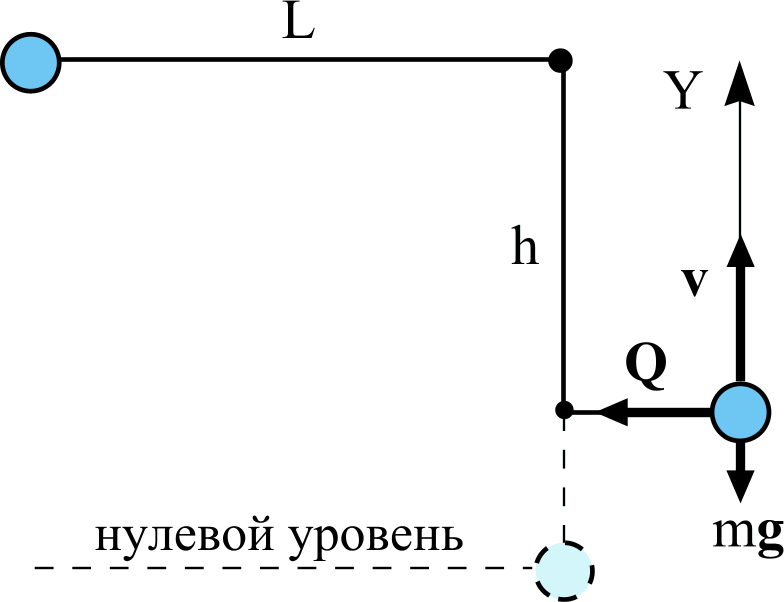
Рассмотрим систему шарик на нити – Земля в двух состояниях. В первом состоянии вся нить с шариком занимает горизонтальное положение. Во втором состоянии меньшая часть нити занимает горизонтальное положение. Система консервативна, поэтом к ней можно применить закон сохранения механической энергии. Выбранный нулевой уровень потенциальной энергии показан на рисунке.

Механическая энергия W₁ системы в первом состоянии – это потенциальная энергия (скорость шарика равна нулю), то есть W₁ = mg L. Во втором состоянии энергия W₂ системы складывается из потенциальной энергии, равной mg (L – h), и кинетической энергии, равной , где v – скорость шарика во втором состоянии системы. Таким образом, W₂ = mg (L – h) + . Поскольку W₁ = W₂, то

mg L = mg (L – h) + , откуда v² = 2gh.

Запишем уравнение второго закона Ньютона для шарика во втором состоянии системы. В инерциальной системе отсчета, связанной с Землей

mg + Q = mа. В проекциях на ось Y: mg_y + Q_y = mа_y. После нахождения проекций, получим:

Q = m . С учетом найденного ранее выражения для v², будем иметь:

Q = m . Так как h = L, то окончательно Q = 4mg.

По третьему закону Ньютона сила натяжения нити равна по величине силе реакции, то есть T = Q. Таким образом, Т = 4mg.

Ответ: Т = 4mg.

Задача 10. На внутренней поверхности полого шара радиуса R, вращающегося вокруг вертикальной оси, находится тело. При каком минимальном коэффициенте трения тело покоится относительно шара, если величина угловой скорости равна ω, радиус сферы, проведенный в точку нахождения тела, составляет с горизонтальной плоскостью угол α. Размерами тела пренебречь.

Дано: R, ω, α.

k − ?

Решение.

Решим задачу в неинерциальной системе отсчета, связанной с вращающимся шаром. Система координат – «естественная»: нормаль направлена к центру кривизны вращения тела (r – радиус кривизны), бинормаль перпендикулярна нормали (направлена вверх по вертикали).

На тело действуют: mg – сила тяжести, направленная вертикально вниз (противоположно бинормали), F_и – сила инерции, направленная вдоль радиуса r вращения тела (противоположно нормали), F_тр – сила трения. Направление этой силы легко найти. Представим, что тело начало скользить по поверхности шара. В этом случае скорость скольжения была бы направлена по касательной к сфере (на рисунке эта скорость не показана). Сила же трения всегда направлена противоположно скорости (в данном случае – противоположно скорости предполагаемого скольжения). И, наконец, − сила нормальной реакции поверхности шара. Эта сила N направлена перпендикулярно силе трения, то есть – к центру шара.

Надеюсь, Вы помните, что и сила трения, и сила нормальной реакции не являются «настоящими» силами, а есть компоненты «настоящей» силы реакции (на рисунке она не показана).

Теперь запишем второй закон Ньютона для вращающегося вместе с шаром тела.

mg + F_и + F_тр + N = 0: ускорение у тела отсутствует, так как тело рассматривается в неинерциальной системе отсчета, связанной с вращающимся шаром.

В проекциях на выбранные оси

mg_n + F_{и n} + F_{тр n} + N_n = 0,

mg_b + F_{и b} + F_{тр b} + N_b = 0.

Найдем проекции. g_n = 0, F_{и n} = − F_и, F_{тр n} = F_тр Cos (90⁰ + α) = − F_тр Sin α,

N_n = N Cos α, g_b =− g, F_{и b} = 0, F_{тр b} = F_тр Cos α, N_b = N Sin α. Тогда

− F_и − F_тр Sin α + N Cos α = 0,

− mg + F_тр Cos α + N Sin α = 0.

Теперь учтем, что F_и = ω² r. Поскольку r = R Cos α, то F_и = ω² R Cos α. Кроме того, F_тр = kN. Подставив все это в предыдущие два уравнения, получим:

N (k Sin α – Cos α) = − m ω² R Cos α,

N (k Cos α + Sin α) = mg.

Получили систему двух уравнений с двумя неизвестными (N и k). Разделив одно уравнение на другое (чтобы избавиться от N), получим:

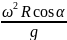= − или

kg Sin α – g Cos α = − kω²R Cos² α – ω²Rsin α Cos α, отсюда

k = .

Ответ: k = .

Задача 11. Тележка массой m совершает «мертвую петлю», скатываясь с наименьшей необходимой для этого высоты (см. рисунок). Определить, с какой по величине силой F_д тележка давит на рельсы в той точке петли, радиус которой составляет угол α с горизонталью. Размерами тележки и трением пренебречь.

Дано: m, α.

F_д − ?

Решение.

Эту задачу решим в неинерциальной системе отсчета, связанной с тележкой. Система координат – «естественная», нормаль направлена к центру кривизны «мертвой петли» (другие оси не понадобятся).

Обозначим точку траектории тележки, где надо найти силу давления на рельсы как А.

В этой точке на тележку действуют: mg – сила тяжести, направленная вертикально вниз, сила нормальной реакции N_А рельсов, направленная вдоль радиуса кривизны траектории к центру и сила инерции F_иА, направленная по радиусу от центра кривизны. Если в результате решения будет найдена величина силы нормальной реакции, то фактически это и будет являться ответом на вопрос задачи, поскольку в соответствии с третим законом Ньютона F_д = N_А.

Теперь запишем второй закон Ньютона для тележки, когда она находится в точке А.

mg + N_А + F_иА = 0. Проектируем на нормаль:

mg_n + N_Аn + F_иАn = 0. После нахождения проекций, получим:

mg Sin α + N_А − F_иА = 0. Поскольку F_иА = , где v_А – величина линейной скорости тележки в точке А, то

N_А = m − mg Sin α. (1)

Для нахождения N_А нужно знать величину скорости тележки в точке А и радиус R. Займемся скоростью.

Рассмотрим систему, состоящую из тележки и Земли в двух состояниях: в момент непосредственно предшествующий скатыванию тележки с высоты Н (см. рисунок) и в момент нахождения тележки в точке А. Система консервативна, поскольку внешние силы N_А и F_иА работы не соверщает, так как направлены перпендикулярно перемещению тележки. Следовательно, механическая энергия системы сохраняется при переходе системы из первого состояния во второе, то есть mgH = m + mg (R Sin α + R). Здесь, mgH – потенциальная энергия системы в первом состоянии, m – кинетическая энергия системы во втором состоянии, mg (R Sin α + R) – потенциальная энергия системы во втором состоянии (выражение в скобках – это высота подъема тележки относительно нулевого уровня потенциальной энергии, который показан на рисунке).

Тогда = 2gH – 2g (R Sin α + R). (2)

Для нахождения Н применим закон сохранения механической энергии при переходе системы из первого состояния в состояние, когда тележка находится в верхней точке «мертвой петли» (на рисунке – точка Б). В этом случае

mgH = m + mg·2R, где m и mg·2R соответственно кинетическая и потенциальная энергии тележки в верхней точке траектории (v_Б – величина скорости в этой точке). Тогда

H = + 2R. (3)

Чтобы найти неизвестную v_Б, применим второй закон Ньютона для тележки в точке Б. При этом будем иметь в виду следующее.

Если тележка скатывается с указанной минимальной высоты Н, то она проходит верхнюю точку «мертвой петли», и обладает необходимой для этого минимальной скоростью в этой точке. Если же тележка будет скатываться с высоты чуть меньшей Н, то тележка верхнюю точку не пройдет и упадет вниз. Но при этом ее контакт с рельсами исчезнет, и сила реакции станет равной нулю. Вот мы и рассмотрим эту критическую ситуацию. В этом случае на тележку будут действовать только сила тяжести mg и сила инерции F_иБ. Второй закон Ньютона запишется так (сразу в модулях):

mg = m , откуда 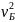= Rg. Подставим это выражение в уравнение (3) и найдем минимальную высоту.

Н = R. Подставляем это выражение в уравнение (2) и находим:

= 3gR – 2gR Sin α.

Теперь легко найти силу реакции из уравнения (1), заменив в этом уравнении предыдущим выражением.

N_А = 3mg (1 – Sin α). Как уже было сказано, F_д = N_А. Следовательно,

F_д = 3mg (1 – Sin α).

Из этой формулы следует, что, когда α → 90⁰ (тело подходит к верхней точке), то F_д → 0, то есть тележка уже «задумывается» о падении вниз.

Ответ: F_д = 3mg (1 – Sin α).

Задача 12. Тело начинает соскальзывать из верхней точки неподвижной полусферы радиусом R, расположенной на горизонтальной поверхности. На какой высоте Н тело оторвется от полусферы, считая от горизонтальной поверхности? Какой угол α с горизонтом составляет радиус полусферы, проведенный в точку отрыва? Какую по величине скорость v будет иметь тело в момент отрыва? Трением и размерами тела пренебречь.

Дано: R.

Н − ? α − ? v − ?

Решение.

Решим задачу в неинерциальной системе отсчета, связанной с движущимся телом.

При скольжении тела на него действуют: mg – сила тяжести, N − сила нормальной реакции полусферы и сила инерции F_и. Направления сил показаны на рисунке.

Запишем второй закон Ньютона для тела сразу в проекциях на нормаль.

mg_n + N_n + F_иn = 0. В момент отрыва тело перестает касаться поверхности полусферы, в результате чего исчезает сила нормальной реакции N. Тогда предыдущее уравнение принимает вид:

mg_n + F_иn = 0.

После нахождения проекций, и, учитывая, что F_и = m , получим:

mg Sin α = m . (1)

Имеем одно уравнение с двумя неизвестными величинами (α и v).

Для получения второго уравнения воспользуемся законом сохранения механической энергии.

Рассмотрим два состояния консервативной системы тело – Земля. В первом состоянии тело находится в верхней точке полусферы и обладает потенциальной энергией mgR (на горизонтальной плоскости потенциальная энергия тела принята равной нулю).

Во втором состоянии тело находится в точке отрыва от полусферы, и ее механическая энергия складывается из потенциальной энергии mgH и кинетической энгергии .

Из рисунка видно, что Н = RSin α, тогда потенциальная энергия тела будет mgRSin α. Таким образом, механическая энергия тела во втором состоянии системы равна mgRSin α + .

В соответствии с законом сохранения механической энергии

mgR = mgRSin α + . (2)

Решая совместно уравнения (1) и (2), находим:

v = ,

Sin α = , откуда α ≈ 42⁰. Ответ: Н = RSin α, α ≈ 42⁰, v = .

Задача 13. Небольшое тело соскальзывает без начальной скорости в яму, имеющую форму полусферы с радиусом R. До глубины R/2 стенки ямы полированные, трение при этом пренебрежимо мало. Далее тело движется с постоянной скоростью. Найти зависимость коэфициента трения k от угла α между горизонталью и радиусом полусферы, проведенным из центра кривизны в точку нахождения тела. Размерами тела пренебречь.

Дано: R.

k = f (α) − ?

Решение.

Решим задачу в неинерциальной системе отсчета, вращающейся вместе с телом. Рассмотрим движение тела в пределах той части ямы, где присутствует сила трения (см. рисунок).

При скольжении тела массой m, на него действуют: mg – сила тяжести (она направлена по вертикали вниз), N − сила нормальной реакции полусферы (направлена к центру кривизны полусферы), F_тр – сила трения (направлена по касательной противоположно направлению скорости движения тела) и сила инерции F_и, которая направлена вдоль радиуса от центра кривизны полусферы.

Запишем второй закон Ньютона для тела.

mg + N + F_тр + F_и = 0. Ноль в правой части уравнения объясняется отсутствием полного ускорения тела. Действительно, нормальное ускорение равно нулю, поскольку выбранная система отсчета вращается вместе с телом относительно центра О. Касательное ускорение тоже отсутствует, так как тело по условию задачи на рассматриваемом участке движется с постоянной скоростью.

Спроектируем это векторное уравнение на нормаль и касательную.

mg_n + N_n + F_{тр n} + F_иn = 0,

mg_τ + N_τ + F_{тр τ} + F_иτ = 0. Находим проекции.

g_n = − g Sin α, N_n = N, F_{тр n} = 0, F_иn = − F_и, g_τ = g Cos α, N_τ = 0, F_{тр τ} = − F_тр, F_иτ = 0. Учтем, что F_и = m где v – величина скорости тела. Тогда

− mg Sin α + N = m , (1)

mg Cos − F_тр = 0. (2).

Найдем величину скорости тела, когда оно достигло глубины R/2, то есть в точке перехода тела из той части полусферы, где трение отсутствовало, в ту ее часть, где тело уже стало двигаться с трением.

Для этого рассмотрим систему тело – Земля в двух состояниях: в момент начала движения и в момент, когда тело находится на глубине R/2. В первом состоянии механическая энергия системы равна mgR. Во втором состоянии энергия системы складывается из кинетической энергии m и потенциальной энергии mg .

Тогда mgR = m + mg , откуда v = .

Из уравнения (1) N = mg Sin α + m . С учетом найденного выражения для скорости

N = mg (1 + Sin α).

Как видим, сила нормальной реакции зависит от угла α, то есть от той точки траектории, где в данный момент находится тело. А поскольку F_тр = kN, то и величина силы трения тоже зависит от угла α, то есть

F_тр = kmg (1 + Sin α). (3)

В то же время из уравнения (2)

F_тр = mg Cos α. (4)

Получается странная, на первый взгляд, вещь: Если по формуле (3) величина силы трения растет с увеличением угла α (с увеличением глубины погружения тела в яму), так как увеличивается синус, то в соответствии с формулой (4) все происходит наоборот, величина силы трения уменьшается, так как с увеличением угла уменьшается косинус. Особенно ярко эта кажущаяся странность проявляется в самой нижней точки траектории, на дне ямы. Действительно, для этой точки α = 90⁰, и величина силы трения в соответствии с (4) тоже равна нулю. А по формуле (3) величина силы трения равна 2kmg.

В чем же дело? Вспомним, как мы получили уравнение (4). Оно является следствием уравнения (2), которое было записано в предположении, что тело после глубины R/2 движется с постоянной по величине скоростью (мы тогда положили, что касательное ускорение равно нулю). Значит, получается, что тело либо не может двигаться с постоянной по величине скоростью, либо, если все-таки оно движется именно так (а в условии задачи утверждается, что v = const), то, чтобы «примирить» правые части уравнений (3) и (4), мы должны сделать вывод, что коэффициент трения есть величина переменная, и в разных точках траектории он разный, то есть зависит от α.

Таким образом, приравнивая правые части уравнений (3) и (4), получим:

k = .

Ответ: k = .

Задача 14. Небольшое тело соскальзывает без начальной скорости в яму, имеющую форму полусферы с радиусом R. До глубины R/2 стенки ямы полированные, трение при этом пренебрежимо мало. Далее тело движется с постоянным коэффициентом трения. Найти коэффициент трения k, если тело останавливается на дне ямы. Размерами тела пренебречь.

Дано: R.

k = − ?

Решение.

В отличие от предыдущей задачи, здесь коэффициент трения постоянен. Тем не менее, сила трения зависит от угла α, поскольку сила нормальной реакции полусферы есть функция этого угла.

При решении задачи будем пользоваться той же системой отсчета, что и в предыдущей.

Рассмотрим систему тело – Земля в двух состояниях: в момент начала движения и в момент, когда тело находится на дне ямы. В первом состоянии механическая энергия системы равна mgR. Во втором состоянии механическая энергия системы равна нулю. Ясно, что закон сохранения механической энергии «не работает», поэтому воспользуемся законом изменения механической энергии.

При переходе системы из первого состояния во второе, механическая энергия изменяется на величину 0 – mgR = − mgR. Это изменение равно работе А_тр только силы трения, так как сила тяжести является внутренней потенциальной силой и не влияет на энергию системы, а нормальная реакция полусферы и сила инерции, являющиеся внешними силами, работы не совершают, поскольку направлены перпендикулярно перемещению тела. Следовательно,

− mgR = А_тр. (1)

Найдем работу силы трения. Вы уже знаете, что для нахождения работы переменной силы, нужно перемещение тела разбить на элементарные (то есть бесконечно малые) участки величиной dr и найти элементарную работу dA_тр на каждом участке, считая, что в пределах таких участков сила трения постоянна, а затем сложить все элементарные работы.

Итак, dA_тр = F_тр dr Cos 180⁰ = − F_тр dr.

При перемещении тела на dr оно поворачивается на элементарный угол dα (см. рисунок 1), причем dα = , что следует из определения угла в радианной мере (dL − это элементарная дуга окружности, по которой движется тело).

Рис. 1

Очевидно, что при бесконечно малом угле поворота, величины перемещения и дуги совпадают, то есть dr = dL, тогда dα = , и dr = R dα. Следовательно,

dA_тр = − F_тр R dα. Учитывая, что F_тр = kmg (1 + Sin α) (см. решение предыдущей задачи), имеем:

dA_тр = − kmg (1 + Sin α) R dα.

Осталось просуммировать все элементарные работы в пределах угла поворота тела при его движении на участке, где действует трение, то есть взять интеграл от левой и правой частей последнего выражения. Интеграл от левой части даст полную работу А_тр. Тогда

A_тр = − kmgR .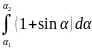

Угол α₁ легко находится по его синусу. Из рисунка 2 видно, что Sin α₁ = = , следовательно, α₁ = . Угол α₂ = .

Рис. 2

Тогда

A_тр = − kmgR = − kmgR ( + ).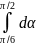

От первого интеграла получим π/2 – π/6, а = = . Следовательно,

A_тр = − kmgR = − 1,9 kmgR.

Подставив это выражение для работы силы трения в уравнение (1), получим:

− mgR = − 1,9 kmgR, откуда k = 0,52.

Ответ: k = 0,52.

Задача 15. Вода течет по квадратной трубе со стороной квадрата d = 0,1 м. Труба расположена в горизонтальной плоскости и имеет закругление радиусом R = 100 м. Найти боковое давление воды, вызванное ее движением по закруглению. Через поперечное сечение трубы в течение времени t₁ = 1 ч протекает масса воды, равная m_t = 100 т. Плотность воды ρ = 10³ .

Дано: d = 0,1 м, R = 100 м, t₁ = 1 ч = 3600 с, m_t = 100 т = 10⁵ кг, ρ = 10³ .

p − ?

Решение.

Решим задачу в неинерциальной системе отсчета, связанной с движущейся водой.

Пусть ∆m – масса воды, находящейся в участке трубы с закруглением, ∆ℓ − длина вдоль трубы этой массы.

На выделенный элемент воды вдоль нормали действуют только две силы: сила инерции F_и и сила реакции трубы Q. Вдоль нормали скорость воды ни по величине, ни по направлению не меняется (она равна нулю), поэтому

F_и + Q = 0. В проекциях на нормаль − F_и + Q = 0 или Q = F_и.

По третьему закону Ньютона вода на трубу действует с силой F_д (силой давления), которая по модулю равна Q. Эта сила направлена противоположно Q и приложена к трубе. Тогда F_д = F_и. Поскольку F_и = (v – величина скорости течения воды), то F_д = . Конечно, разные части выделенного элемента воды находятся на разных расстояниях от центра кривизны, но, поскольку R >> d, мы этим пренебрегаем и для определения величины силы инерции, а, значит, и силы давления, используем расстояние R.

Давление, оказываемое на закругленный участок трубы, p = = где ∆S – площадь соприкосновения воды массой ∆m с тем участком трубы, на который действует сила F_д. Очевидно, ∆S = d·∆ℓ. Тогда p = .

Масса ∆ m = ρ·∆v, где ∆v – объем выделенного участка воды. Так как

∆v = d·∆S = d²·∆ℓ, то ∆ m = ρ·d²·∆ℓ. Тогда давление

p = . (1)

Осталось найти величину скорости.

Вся масса воды, которая в начальный момент времени (t₀ = 0) стала пересекать поперечное сечение s трубы, через время t₁ займет объем, равный s·L, где L – то расстояние вдоль трубы, на которое переместились частицы воды, первыми пересекшие поперечное сечение трубы в начальный момент времени. Масса воды в этом объеме m_t = s·L·ρ. Так как L = v·t₁, то m_t = s·v·t₁·ρ. Отсюда v = . Учитывая, что s = d², v = . Подставив это выражение в формулу (1), получим:

p = . Подставив числа, получим: p = 7,7 Па.

Ответ: p = 7,7 Па.