§ 12.4. Энергия, работа, импульс

Задача 1. Камень брошен с высоты h под некоторым углом к горизонту с начальной скоростью, величина которой v₀. Найти величину скорости v₂ в момент падения камня на землю. Сопротивлением воздуха пренебречь.

Дано: h, v₀.

v₂ − ?

Решение.

Эта задача может быть решена с помощью законов кинематики, однако, использование закона сохранения механической энергии позволяет решить задачу значительно проще.

Система Земля – камень является консервативной, поскольку в ней внутренняя сила взаимодействия между камнем и Землей (сила тяжести) зависит от координат. Следовательно, к системе применим закон сохранения механической энергии. В дальнейшем, при решении других задач, полную механическую энергию системы мы для краткости будем называть просто энергией системы, поскольку в механике, в основном, рассматривается только этот вид энергии.

Рассмотрим энергию системы в двух состояниях: сразу после бросания камня и после падения камня на Землю. Энергия системы в первом состоянии

Е₁ = Т_к1 +Т_З1 + U₁, энергия системы во втором состоянии Е₂ = Т_к2 +Т_З2 + U₂, где Т_к1 и Т_к2 – кинетические энергии камня в первом и втором состояниях соответственно, Т_З1 и Т_З2 − кинетические энергии Земли в первом и втором состояниях соответственно, U₁ и U₂ – потенциальные энергии взаимодействия камня и Земли в первом и втором состояниях соответственно.

Тогда Е₁ = Е₂ или Т_к1 +Т_З1 + U₁ = Т_к2 +Т_З2 + U₂ . Иначе,

(Тк₂ − Тк₁) + (Т_З2−Т_З1) + (U₂ − U₁) = 0.

(Тк₂ − Тк₁) = ΔТ_к – это – изменение кинетической энергии камня при переходе системы из первого состояния во второе;

(Т_З2−Т_З1) = ΔТ_З – это – изменение кинетической энергии Земли при переходе системы из первого состояния во второе;

(U₂ − U₁) = ΔU – это – изменение потенциальной энергии взаимодействия Земли и камня при переходе системы из первого состояния во второе.

Тогда ΔТ_к + ΔТ_З + ΔU = 0. Оказывается, что величиной ΔТ_З можно пренебречь. Тогда выражение для закона сохранения энергии системы упростится:

ΔТ_к + ΔU = 0. (1)

Покажем, что изменение кинетической энергии Земли при переходе системы из одного состояния в другое можно не учитывать. Рассмотрим Землю и камень в какой-то инерциальной системе отсчета, например, связанной с Солнцем. Пусть в этой системе скорость Земли в первом состоянии u₁, а во втором состоянии эта скорость равна u₂. Аналогичные скорости для камня v₁ и v₂. Поскольку система Земля – камень является не только консервативной, но еще и замкнутой, то применим к ней закон сохранения количества движения:

Мu₁ + mv₁ = Мu₂ + mv₂ или М(u₂ − u₁) = m(v₁ − v₂), где М – масса Земли, m – масса камня. Тогда u₂ − u₁ = 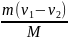. Поскольку m << М, то u₂ − u₁ = 0, откуда u₂ = u₁, то есть скорость Земли практически не изменяется. Отсюда и следует, что кинетическая энергия Земли при переходе системы из одного состояния в другое практически не изменяется или, что то же самое, изменение этой энергии равно нулю. В дальнейшем, когда в рассматриваемых системах будет фигурировать Земля, мы это положение (то, что ΔТ_З = 0) всегда будем иметь в виду.

Рассмотрим движение камня в системе отсчета, связанной с Землей.

Изменение кинетической энергии камня ΔТ_к = − . Изменение потенциальной энергии взаимодействия системы ΔU = 0 – mgh. Тогда уравнение (1) примет вид:

− – mgh = 0, откуда находим v₂ = .

При решении задачи мы выбрали систему Земля – камень. Вообще, мы вправе в качестве системы выбирать любые тела и в любом их количестве, это определяется условием задачи и удобством ее решения. Так, в данной задаче мы в качестве системы могли бы выбрать камень. Но тогда сила тяжести, действующая на камень со стороны Земли, уже не будет являться внутренней силой, а будет внешней по отношению к данной системе (камню). В этом случае закон сохранения энергии «не работает», и мы должны применить закон изменения энергии: изменение кинетической энергии камня равно работе внешней силы, то есть − = А_внеш. Мы уже знаем, что работа силы тяжести в этом случае равна mgh. Следовательно, − = mgh, то есть получено то же уравнение, что и раньше, и выражение для v₂ будет тем же. Понятно, что при таком подходе, то есть когда мы в качестве системы выбираем один только камень, о потенциальной энергии мы уже не говорим. Такого понятия в данном случае просто не существует.

Оно возникает, когда речь идет о взаимодействии объектов. Но тогда в систему надо включать и камень, и Землю, что мы и сделали ранее.

Ответ: v₂ = .

Задача 2. Пуля массой m = 20 г, выпущена с поверхности Земли под углом α к горизонту с начальной скоростью, величина которой v₀ = 600 м/с. В верхней точке траектории пуля имеет кинетическую энергию Т = 900 Дж. Найти угол α. Сопротивлением воздуха пренебречь.

Дано: m = 20 г =2∙10⁻² кг, v₀ = 600 м/с, Т = 900 Дж.

α − ?

Решение.

Рассмотрим систему Земля – пуля последовательно в двух состояниях. Первое состояние соответствует моменту, когда пуля только вылетела и имеет величину скорости v₀, а второе – моменту, когда пуля достигла верхней точке траектории.

Земля и пуля представляют собой консервативную систему, поскольку между ними действует только потенциальная сила тяжести, а внешние силы отсутствуют. Следовательно, к системе применим закон сохранения энергии. Запишем его в виде ΔТ + ΔU = 0, где ΔТ = Т − – изменение кинетической энергии системы при ее переходе из первого состояния во второе, ΔU = mgH – изменение потенциальной энергии взаимодействия между Землей и пулей при том же переходе. Находя ΔU, мы учли, что начальная потенциальная энергия (когда пуля находилась на уровне Земли) равна нулю. В последней формуле H – это максимальная высота подъема пули. Из кинематики известно, что Н = (см. решение задачи 11.2.13). Тогда ΔU = mg . Следовательно,

Т − + m = 0.

Отсюда легко найти, что Sin² α = 1 − .

Тогда Sin α = . Подставив числа, получим Sin α = 0,866, откуда α = 60⁰.

Ответ: α = 60⁰.

Задача 3. Человек, имеющий массу М, прыгает под углом α к горизонту со скоростью, величина которой v₀. В верхней точке траектории он бросает вертикально вниз груз массой m со скоростью, равной по величине v₁. На какую общую высоту H_max подпрыгнул человек?

Дано: М, α, v₀, v₁, m.

H_max − ?

Решение.

Рассмотрим систему Земля – человек в двух состояниях. Первое состояние соответствует моменту, когда человек бросил груз. Практически и человек и груз в этот момент находятся в верхней точке траектории. Второе состояние выбранной системы соответствует моменту, когда человек находится на высоте H_max.

В течение перехода системы из первого состояния во второе в ней действует консервативная сила тяжести, следовательно, к системе применим закон сохранения энергии.

К инетическая энергия человека в первом состоянии равна Т₁ = , где u – величина скорости человека сразу после того, как он бросил груз. Очевидно (см. рисунок) u = u₁ + u₂, где u₁ – это «добавочная» скорость, которую человек получил в результате того, что бросил груз, u₂ – это скорость движения человека по горизонтали. Движение человека в горизонтальном направлении не изменяется, поскольку в этом направлении он движется без ускорения. Поэтому величина этой скорости всегда равна u₂ = v₀ Cos α. Тогда

= .

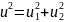Следовательно,

Т₁ = + .

Потенциальная энергия человека в первом состоянии

U₁ = Mg H, где H – высота верхней точки траектории, где человек бросил груз.

Во втором состоянии человек прекратил свое движение вверх, он достиг высоты H_max, но по горизонтали он продолжает свое движение с прежней скоростью.

Тогда кинетическая энергия человека во втором состоянии Т₂ = . Потенциальная энергия человека в этом состоянии U₂ = Mg H_max. Теперь мы можем написать:

T₁ + U₁ = T₂ + U₂ или + + Mg H = + Mg H_max. Отсюда находим H_max = H + .

Если бы мы знали Н и u₁, то задача была бы решена. Но эти величины легко найти. Действительно, из кинематики Н = . Величину u₁ найдем, воспользовавшись законом сохранения импульса системы человек – груз. Рассмотрим эту систему в двух состояниях. В первом состоянии человек с камнем находятся на высоте Н, и человек принял решение бросить груз (но еще не бросил). Второе состояние соответствует моменту, наступившему спустя мгновенье после того, как груз был брошен (для системы Земля – человек оно соответствует первому состоянию). Силы, действующие между человеком и грузом, являются внутренними для рассматриваемой системы, поэтому они не изменяют ее количества движения. Правда, на систему действуют внешние силы, это – силы тяжести человека и груза. Однако человек избавляется от груза за очень короткое время, и за это время внешние силы практически не успеют сколь-нибудь значительно изменить импульс системы.

Поэтому мы будем считать, что импульс системы не изменяется при ее переходе из первого состояния во второе. Проекция общего импульса системы на вертикальную ось (пусть она направлена вверх) в первом состоянии равна нулю, поскольку в этот момент скорость человека с камнем направлена по горизонтали. Во втором состоянии эта проекция равна Mu₁ – mv₁. Тогда Mu₁ – mv₁ = 0, откуда u₁ = . Теперь легко найти общую высоту:

H_max = + .

Почему, когда мы рассматривали вторую систему, то воспользовались законом сохранения импульса, а не законом сохранения энергии? Ведь, мы могли бы рассмотреть систему Земля – человек – груз в выбранных состояниях. Казалось бы, что эта система должна быть консервативной, поскольку сила тяжести – это потенциальная сила, она является консервативной силой и не изменяет энергии системы. Нет, такая система консервативной не является. Не надо забывать, что внутренние силы, действующие между человеком и грузом при его бросании, это – неконсервативные силы, они-то и делают такую систему неконсервативной. Что же касается закона сохранения импульса, то ему «все равно» какие в системе действуют силы. Он «всеядный», для него главное, чтобы внешних сил не было (или их действием можно пренебречь), и тогда он «заработает».

И – последнее. Не обязательно прибегать к закону сохранения энергии при решении этой задачи. Можно было бы сразу найти u₁, воспользовавшись законом сохранения импульса, а затем, применив законы кинематики, найти тот «кусочек» высоты, который человек получит в результате бросания груза. Будет полезно, если Вы самостоятельно сделаете это, заодно и кинематику повторите. Естественно, результат должен быть такой же.

Ответ: H_max = + .

Задача 4. Камень массой m = 0,1 кг, соскользнув с закрепленной наклонной плоскости высотой h = 3 м, приобрел в конце ее скорость, величина которой v = 6 м/с. Найти работу А_тр сил трения. Величина начальной скорости камня v₀ = 0.

Дано: m = 0,1 кг, h = 3 м, v = 6 м/с, v₀ = 0.

А_тр − ?

Решение.

Эта задача не может быть решена с помощью формулы А = F_тр∙Δr (F_тр – сила трения, Δr – вектор перемещения), если неизвестны угол наклона плоскости и ее длина. Для решения задачи воспользуемся законом изменения энергии.

Рассмотрим систему Земля – камень последовательно в двух состояниях. Первое состояние соответствует нахождению камня на высоте h над основанием плоскости, а второе – в конце плоскости, когда камень приобрел скорость, по величине равную v.

Помимо Земли камень взаимодействует с плоскостью, со стороны которой на него действует сила реакции R = N + F_тр, где N – сила нормальной реакции плоскости.

Поскольку R является внешней для системы силой, то эта система не является консервативной, и именно работа этой силы и вызывают изменение полной энергии системы. Внутренняя же сила, сила тяжести, является потенциальной и к изменению энергии отношения не имеет. Тогда ΔТ_к + ΔU = А_R. Здесь, ΔТ_к – изменение кинетической энергии камня при переходе системы из первого состояния во второе, ΔU – изменение потенциальной энергии взаимодействия между камнем и Землей при тех же условиях, А_R – работа силы R. Напомню, что изменением кинетической энергии Земли мы пренебрегаем, о чем уже подробно говорилось ранее.

Работа силы реакции А_R = (N + F_тр)∙Δr = N∙Δr + F_тр∙Δr. Величина N∙Δr – это работа силы нормальной реакции плоскости, а F_тр∙Δr – это работа силы трения. Работа силы нормальной реакции плоскости равна нулю, так как векторы N и Δr перпендикулярны друг другу, а, значит, косинус угла между ними равен нулю. Тогда А_R = А_тр, следовательно, ΔТ_к + ΔU = А_тр.

Изменение кинетической энергии камня ΔТ_к = Т_к2 − Т_к1, где

Т_к2 = − кинетическая энергия камня во втором состоянии системы, Т_к1 − кинетическая энергия камня в первом состоянии системы. Очевидно, Т_к1 = 0, так как v₀ = 0. Тогда ΔТ_к = .

Изменение потенциальной энергии ΔU = U₂ – U₁, где U₂ = 0 − потенциальная энергия во втором состоянии системы, U₁ = mgh − потенциальная энергия в первом состоянии системы. Тогда ΔU = − mgh. Равенство нулю U₂ объясняется так называемым условием нормировки потенциальной энергии. Условие нормировки – это выбор уровня, на котором определяется начальное значение потенциальной энергии и выбор величины и знака начального значения этой энергии. Условие нормировки выбирается произвольно. Так в данном случае за уровень, от которого отсчитывается потенциальная энергия, принят уровень основания наклонной плоскости, а величина этой энергии на данном начальном уровне принята равной нулю. Произвол в нормировке объясняется тем, что в большинстве случаев интерес представляет не само значение потенциальной энергии, а разность ее значений на различных уровнях. Когда вычисляется эта разность, то начальное значение потенциальной энергии просто исчезает. Поясню это на примере. Допустим, в данной задаче за начальный уровень мы взяли не основание наклонной плоскости, а поверхность Земли, а за начальное значение потенциальной энергии (то есть ее значение на начальном уровне) – какую-то произвольную величину (неважно какую) U₀. Тогда U₁ = mgh + U₀, а U₂ = U₀. Изменение потенциальной энергии ΔU = U₂ – U₁ = − mgh. То есть мы получили то же значение, что и при первоначальном условии нормировки.

Итак, выражение ΔТ_к + ΔU = А_тр принимает вид:

А_тр = – mgh.

Подставив числа, получим А = − 1,2 Дж.

Ответ: А = − 1,2 Дж.

Задача 5. Небольшое тело начинает скользить с вершины закрепленной на горизонтальной поверхности наклонной плоскости, высота которой Н. Считая, что трение отсутствует, определить характер движения тела после того, как оно покинет наклонную плоскость, если удар тела о горизонтальную плоскость абсолютно упругий. Плоскость наклонена к горизонту под углом α.

Дано: Н, α.

Определить характер движения тела после абсолютно упругого удара о горизонтальную плоскость.

Решение.

Рассмотрим систему Земля – тело в двух состояниях. Первое состояние соответствует моменту, когда тело только начинает скользить по наклонной плоскости, имея нулевую начальную скорость. Во втором состоянии тело находится у основания наклонной плоскости за мгновенье до удара о горизонтальную поверхность (см. рисунок)

Д анная система консервативна, поскольку внутренняя сила – это потенциальная сила тяжести, которая не изменяет энергии системы. Внешняя сила – это сила нормальной реакции плоскости, и ее работа равна нулю, так как направление этой силы перпендикулярно перемещению тела.

Для консервативной системы ΔТ + ΔU = 0, где ΔТ = Т₂ – Т₁ – изменение кинетической энергии системы при ее переходе из первого состояния во второе, ΔU = U₂ – U₁ – изменение потенциальной энергии системы при тех же условиях.

Конечное значение кинетической энергии тела Т₂ = (m – масса тела, v – величина скорости тела во втором состоянии). Начальное значение кинетической энергии равно нулю, поскольку тело начинает движение без начальной скорости. Изменением кинетической энергии Земли, как уже нам известно, пренебрегаем. Конечное значение потенциальной энергии тела U₂ = 0, таково наше условие нормировки. Начальное значение потенциальной энергии U₁ = mgH.

Тогда – mgH = 0, откда v = .

При абсолютно упругом ударе о горизонтальную поверхность, тело отскакивает от нее с такой же по величине скоростью, как и при ударе.

Обозначим скорость при отскоке как v₀. Тогда v₀ = . Кроме того, при таком ударе угол отскока равен углу падения тела на горизонтальную поверхность (углы отсчитываются по отношению к перпендикуляру к горизонтальной поверхности в точке удара).

В дальнейшем тело будет вести себя так же, как в задаче 11.2.13, за исключением того, что завершив свое движение по параболе, оно «не успокоится», а вновь упруго отразится от горизонтальной поверхности и т. д.

Максимальная высота, на которую поднимется тело при отскоке

h = = H Sin² α.

Расстояние по горизонтали между точками соударения тела с горизонтальной плоскостью

L = = 2H Sin 2α.

Ответ: тело будет совершать периодические движения по параболе.

Задача 6. Клин, масса которого М, находится на горизонтальной плоскости и может перемещаться по ней без трения. По клину скользит груз, масса которого m. Трение между грузом и клином отсутствует. Считая, что в начальный момент времени система клин – груз находится в покое, определить относительно Земли величину v скорости клина и величину u скорости груза в тот момент, когда груз опустится по вертикали на высоту h. Угол при основании клина равен α.

Дано: М, m, h, α.

v − ? u − ?

Решение.

Рассмотрим систему клин – груз в двух состояниях. Первое состояние соответствует моменту, когда груз только начинает скользить по наклонной плоскости, имея нулевую начальную скорость. Во втором состоянии тело находится на высоте h от основания клина.

Для решения задачи нам придется воспользоваться законом сохранения импульса системы в горизонтальном направлении, законом изменения энергии, а также учесть то, что при движении груза угол α с горизонтальной плоскостью составляет не скорость u, которая определяется по отношению к Земле и величину которой надо найти, а скорость груза относительно клина, то есть относительная скорость u_от. При движении груза, клин также перемещается по горизонтальной плоскости с какой-то скоростью v по отношению к Земле. Являясь для клина абсолютной скоростью, она в то же время будет переносной скоростью для груза. Тогда на основании закона сложения скоростей u = u_от + v. Спроектируем это векторное уравнение на координатные оси X и Y, выбранные так, как показано на рисунке.

u _x = u_{от x} + v_x, u_y = u_{от y}+ v_y. Так как

u_{от x} = u_от Cos α, v_x = − v,

u_{от y} = − u_от Sin α, v_y = 0, то

u_x = u_от Cos α − v,

u_y = − u_от Sin α или

u_от Cos α = v + u_x,

u_от Sin α = − u_y. Тогда tg α = − , откуда

u_y = − (v + u_x) tg α. (1)

Выбранная система по отношению к горизонтальному направлению является замкнутой. Действительно, внешние силы (силы тяжести груза и клина) направлены вертикально и не изменяют импульса системы по горизонтали. В первом состоянии этот импульс равен нулю (система покоилась). Во втором состоянии проекция общего импульса системы на горизонтальную ось равна

Mv_x + mu_x. Тогда mu_x – Mv = 0, откуда

u_x = . (2)

В то же время данная система не является консервативной, несмотря на то, что внутренние неконсервативные силы в системе отсутствуют. На систему действуют внешние силы тяжести, и их работа равна изменению кинетической энергии системы. О потенциальной энергии говорить не приходится, поскольку Земля не является объектом системы (об этом говорилось в решении задачи 12.4.1). Тогда ΔТ = А_внеш, где ΔТ = ΔТ₁ + ΔТ₂ – изменение кинетической энергии системы при ее переходе из первого состояния во второе, А_внеш – общая работа силы тяжести груза и силы тяжести клина.

Изменение кинетической энергии груза ΔТ₁ = – 0 = . Изменение кинетической энергии клина ΔТ₂ = – 0 = .

Работа силы тяжести клина равна нулю, так как клин движется перпендикулярно своей силе тяжести. Работа силы тяжести груза равна mgh, поэтому А_внеш = mgh. Следовательно,

= mgh. (3)

Для дальнейшего решения будет удобнее представить квадрат модуля скорости груза как сумму квадратов ее проекций, то есть u² = + . Это связано с тем, что в предыдущих уравнениях (1) и (2) фигурируют именно проекции этой скорости. Тогда

+ + = mgh (4).

Итак, мы имеем три уравнения (1), (2), (4) с тремя неизвестными u_x, u_y, v, и можно считать, что в принципе задача решена. Осталось просто выполнить техническую работу – решить систему трех уравнений с тремя неизвестными (u_x, u_y, v).

Заменим u_y в (4) выражением из (1).

В результате получим + = mgh.

Теперь в это уравнение вместо u_x подставим его выражение из (2).

Тогда + = mgh. Получено одно уравнение с одним неизвестным. После его решения будем иметь

v = .

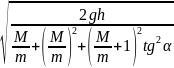Абсолютную скорость груза найдем из (3), подставив туда последнее выражение для v. В результате получим

u = · . Ответ: v = ,

u = · .

Задача 7. Тело массы m = 1 кг скользит без трения по гладкому горизонтальному столу и въезжает на подвижную горку массы M = 5 кг. Высота горки H = 1,2 м. Трение между горкой и столом отсутствует. Найти величину v₁ конечной скорости тела и величину v₂ конечной скорости горки. Величина начальной скорости тела v₀ = 5 м/с.

Дано: m = 1 кг, M = 5 кг, H = 1,2 м, v₀ = 5 м/с.

v₁ − ? v₂ − ?

Решение.

Рассмотрим систему тело – горка в двух состояниях. Первое состояние соответствует моменту, когда тело еще находится на горизонтальном столе, а горка неподвижна. Во втором состоянии тело уже находится на горизонтальном столе, покинув горку. Очевидно, что тело может соскользнуть с горки, так и не достигнув высоты Н, а может быть и так, что тело перевалит эту высоту и спустится с горки уже по другому склону. Однако о том, какая из этих возможностей реализуется в действительности, мы поговорим позже. А пока рассмотрим выбранную систему в этих двух состояниях.

Импульс системы в горизонтальном направлении не изменяется при ее переходе из одного состояния в другое, поскольку в этом направлении на систему не действуют никакие силы. Поэтому p_1x = p_2x, где p_1x = mv_0x ‒ проекция импульса системы на ось Х в первом состоянии, p_2x = mv_1x + Mv_2x ‒ то же во втором состоянии. При выбранном направлении оси Х (см. рисунок) v_0x = v₀, v_2x = v₂ (будем считать, что это очевидно), а вот знак v_1x нам пока неизвестен, поскольку мы еще не знаем по какому склону будет соскальзывать тело с горки. Поэтому mv₀ = mv_1x + Mv₂, откуда

v_1x =v₀ ‒ v₂ (1).

Изменения полной энергии системы также не происходит, поскольку внешние силы (сила тяжести тела и сила тяжести горки) работы не совершают, так как они перпендикулярны перемещениям, которые были совершены элементами системы при ее переходе из первого состояния во второе. То же самое можно сказать и о внутренних силах системы (силе нормальной реакции горки и силе нормального давления тела на горку): они всегда перпендикулярны соответствующим перемещениям при движении элементов системы. Хотя в процессе самого перехода кинетические энергии тела и горки меняются.

Напоминаю, что о потенциальной энергии взаимодействия элементов системы с Землей мы не говорим, так как Земля не входит в систему.

Изменение кинетической энергии тела ΔТ_т = ‒ , а изменение кинетической энергии горки ΔТ_г = . Следовательно,

+ = 0. (2)

Очевидно, что = . Тогда с учетом (1) = .

Подставив это выражение в (2), после несложных преобразований получим ‒ 2v₀v₂ = 0. Сокращать на v₂ не следует из-за опасения потерять корень v₂ = 0.

Последнее уравнение имеет два возможных решения: 1) v₂ = 0 и 2) v₂ = . В соответствии с (1) v_1x тоже принимает два возможных значения: 1) v_1x = v₀ и

2) v_1x = v₀ . Видно, что значения v₂ = 0, v_1x = v₀ соответствуют случаю, когда тело перевалило горку (v_1x > 0, так как проекция равна модулю начальной скорости, следовательно, вектор v₁ направлен так же, как и ось Х).

В этом случае v₁ = v₀. Если же v₂ = , а v_1x = v₀ , то это годится для ситуации, когда тело, не добравшись до вершины горки, повернуло назад и соскользнуло с горки по тому же склону, по которому и поднималось. В этом случае v₁ = .

Осталось выяснить, какой из двух возможных вариантов реализуется в нашем случае. Для этого забудем на время, что высота горки H = 1,2 м, а зададимся вопросом, на какую максимальную высоту Н₁ при заданных v₀, m и M сможет подняться тело? Очевидно, что на этой высоте скорость тела по отношению к горке (относительная скорость) будет равна нулю. Поскольку абсолютная скорость тела (по отношению к Земле) равна сумме относительной и переносной скоростей, а переносной скоростью является скорость горки относительно Земли (она же ‒ абсолютная скорость горки), то получается, что на высоте Н₁ абсолютные скорости тела и горки совпадают. Обозначим эту скорость как v.

Теперь рассмотрим систему тело ‒ горка в двух состояниях. Первое состояние то же, что и в начале решения задачи: тело еще находится на горизонтальном столе, а горка неподвижна. Второе же состояние будет соответствовать моменту, когда тело окажется на высоте Н₁. Закон сохранения импульса при переходе системы из первого состояния во второе опять же «работает», но математически он уже будет выглядеть так (запишем сразу в модулях):

mv₀ = (m + M) v. (3)

А вот закон сохранения энергии в данном случае уже не выполняется, поскольку сила тяжести тела совершает работу при подъеме тела на высоту Н₁, и эта работа равна изменению кинетической энергии системы. Изменение кинетической энергии тела равно ‒ , а изменение кинетической энергии горки равно . Работа же силы тяжести тела равна ‒ mgH₁.

Тогда ‒ + = ‒ mgH₁.

Решая это уравнение совместно с (3), найдем Н₁ = . Подставив числа, получим Н₁ = 1,04 м. Поскольку реальная высота горки Н = 1,2 м, то тело «не дотянет» до ее вершины и его движение вниз к столу будет происходить по тому же склону, по которому оно поднималось.

Таким образом, для данной задачи v₁ = , v₂ = .

Подставляя числовые значения величин, получаем v₁ = 3,3 м/с, v₂ = 1,7 м/с.

Ответ: v₁ = 3,3 м/с, v₂ = 1,7 м/с.

Задача 8. Первый шар массой m₁ = 2 кг движется со скоростью, величина которой v₁ = 3 м/с. Второй шар массой m₂ = 8 кг движется со скоростью, величина которой v₂ = 1 м/с. Найти скорость u₁ первого шара и скорость u₂ второго шара сразу после удара, если: а) шары движутся навстречу друг другу; б) первый шар догоняет второй. Удар считать центральным и абсолютно упругим.

Дано: m₁ = 2 кг, v₁ = 3 м/с, m₂ = 8 кг, v₂ = 1 м/с.

u₁ − ? u₂ − ?

Решение.

Рассмотрим систему, состоящую из шаров в двух состояниях: за мгновенье до удара (первое состояние) и, спустя мгновенье ‒ после (второе состояние). Система не является замкнутой, поскольку на нее действуют внешние силы (силы тяжести шаров). Тем не менее, считая удар кратковременным, полагаем, что за время удара внешние силы практически не успеют изменить общего импульса системы, поэтому к ней можно применить закон сохранения количества движения. Проекция общего импульса системы на ось Х до удара p_1x = m₁v_1x + m₂v_2x, а после удара p_2x = m₁u_1x + m₂u_2x.

Так как p_1x = p_2x, то

m₁v_1x + m₂v_2x = m₁u_1x + m₂u_2x. (1)

Данную систему за время перехода из первого состояния во второе можно считать консервативной, так как внутри системы отсутствуют диссипативные силы (удар абсолютно упругий), а работа внешних сил за это время равна нулю (перемещения шаров в течение удара практически не происходит). Следовательно, ΔТ₁ + ΔТ₂ = 0, где

ΔТ₁ = 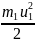‒ ‒ изменение кинетической энергии первого шара при переходе системы из первого состояния во второе,

ΔТ₂ = ‒ ‒ изменение кинетической энергии второго шара при тех же условиях. Тогда

‒ + ‒ = 0.

Запишем последнее уравнение иначе: m₁ = m₂ .

Так как = , а = , то последнюю формулу можно представить так:

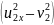m₁ = m₂ . (2)

Пусть ось направлена в сторону движения первого шара.

а). После нахождения проекций, выражение (1) примет вид:

m₁v₁ ‒ m₂v₂ = m₁u_1x + m₂u_2x. Проекции скоростей шаров после удара нам не известны, поскольку мы пока не знаем направления этих скоростей. Запишем последнюю формулу иначе:

m₁ (v₁ ‒ u_1x) = m₂ (v₂ + u_2x). (3)

Итак, мы имеем систему двух уравнений (2) и (3) с двумя неизвестными u_1x и u_2x. Решим ее. Поделив (2) на (3), получим v₁ + u_1x = u_2x ‒ v₂, откуда

u_2x = v₁ + v₂ + u_1x. (4)

Подставив это выражение для u_2x в (3), после несложных преобразований найдем

u_1x = . (5)

Модуль этой скорости u₁ = .

Из (4) с учетом найденного выражения для u_1x найдем:

u_2x = . (6)

Модуль этой скорости u₂ = .

Подставив числовые значения, получим

u_1x = ‒ 3,4 м/с, u₁ = 3,4 м/с.

u_2x = 0,6 м/с, u₂ = 0,6 м/с.

Таким образом, первый шар после столкновения изменил направление своей скорости на противоположное, увеличив при этом величину скорости. Второй шар после удара также изменил направление первоначального движения, уменьшив при этом величину скорости.

б). После нахождения проекций, выражение (1) примет вид:

m₁v₁ + m₂v₂ = m₁u_1x + m₂u_2x. Иначе:

m₁ (v₁ ‒ u_1x) = m₂ (u_2x ‒ v₂). (5)

Можно было бы для второго шара вместо u_2x написать u₂, поскольку, очевидно, что, если его подтолкнул первый шар в направлении первоначального движения (в нашем случае в направлении оси Х), то в том же направлении второй шар и будет двигаться после удара. Однако оставим как есть, от этого ничего не изменится.

Решая систему, состоящую из уравнений (2) и (5) так же, как мы это делали в первом случае, найдем

u_1x = . Модуль этой скорости

u₁ = .

u_2x = . Модуль этой скорости

u₂ = .

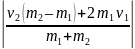Подставив числовые значения, получим

u_1x = ‒ 0,2 м/с, u₁ = 0,2 м/с.

u_2x = 1,8 м/с, u₂ = 1,8 м/с.

Таким образом, первый шар после столкновения изменил направление своей скорости на противоположное, уменьшив при этом величину скорости. Второй шар после удара продолжил движение в прежнем направлении (как мы и предполагали), но с увеличенной скоростью.

Ответ: а) u_1x = ‒ 3,4 м/с, u₁ = 3,4 м/с, u_2x = 0,6 м/с, u₂ = 0,6 м/с,

б) u_1x = ‒ 0,2 м/с, u₁ = 0,2 м/с, u_2x = 1,8 м/с, u₂ = 1,8 м/с.

Задача 9. Первый шар массой m₁ = 5 кг ударяется о неподвижный второй шар массой m₂ = 2,5 кг, который сразу после удара приобрел кинетическую энергию = 5 Дж. Считая удар центральным и абсолютно упругим, найти кинетическую энергию Т₁ первого шара непосредственно перед ударом и кинетическую энергию этого шара сразу после удара.

Дано: m₁ = 5 кг, m₂ = 2,5 кг, = 5 Дж.

Т₁ − ? − ?

Решение.

Ситуация похожа на ту, что рассматривалась в предыдущей задаче, только величина скорости второго тела до удара имеет другое значение (в данной задаче эта величина равна нулю). В остальном же все то же самое. Поэтому при необходимости сразу воспользуемся некоторыми результатами решения задачи 12.4.8.

Кинетическая энергия первого шара непосредственно перед ударом Т₁ = , где v₁ ‒ величина скорости первого шара за миг до удара. Кинетическая энергия первого шара сразу после удара = , где u₁ ‒ величина скорости первого шара в указанное мгновенье. Поскольку = , то = .

Вначале займемся Т₁.

Формула (6) предыдущей задачи с учетом того, что v₂ = 0 будет выглядеть так:

u_2x = . Отсюда v₁ = , а = .

Поскольку = = , то = . Тогда = . Подставив это выражение в формулу Т₁ = , получим: Т₁ = . С учетом числовых значений Т₁ = 5,6 Дж.

Перейдем к нахождению

Формула (5) предыдущей задачи с учетом того, что v₂ = 0 будет выглядеть так:

u_1x = 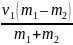. Тогда = 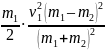. Формулу, связывающую и , мы уже нашли. Подставив ее в последнее выражение, получим: = . С учетом чисел = 0,6 Дж.

Ответ: Т₁ = 5,6 Дж, = 0,6 Дж.

Задача 10. Два шара движутся навстречу друг другу и соударяются абсолютно неупруго. Величина скорости первого шара до удара v₁ = 2 м/с, величина скорости второго шара до удара v₂ = 4 м/с. Величина общей скорости шаров сразу после удара u = 1 м/с. По направлению u совпадает с v₁. Во сколько раз кинетическая энергия Т₁ первого шара была больше кинетической энергии Т₂ второго шара?

Дано: v₁ = 2 м/с, v₂ = 4 м/с, u = 1 м/с.

− ?

Решение.

Так как Т₁ = , а Т₂ = , то = , где m₁ ‒ масса первого шара, m₂ масса второго шара.

Учитывая кратковременность удара, применим к шарам закон сохранения импульса. В проекциях на ось Х этот закон в данном случае имеет вид

m₁v_1x + m₂v_2x = (m₁ + m₂) u_x.

Направим ось в сторону движения первого шара. После нахождения проекций, будем иметь m₁v₁ ‒ m₂v₂ = m₁ u + m₂ u.

Поделим обе части равенства на m₂: ‒ = + u, откуда = .

Тогда = . Подставив числа, получим = 1,25.

Ответ: = 1,25.

Задача 11. На гладкой горизонтальной поверхности на некотором расстоянии от вертикальной стенки покоится шар массы М. Другой шар, масса которого m, скользит с некоторой скоростью по направлению от стенки к первому шару. Между шарами происходит центральный упругий удар. При каком соотношении второй шар после удара достигнет стенки и, упруго отразившись от нее, догонит первый шар?

Дано: М, m.

− ?

Решение.

Рассмотрим систему, состоящую из шаров в двух состояниях: непосредственно перед столкновением и сразу после удара.

Считая систему замкнутой, применим к ней закон сохранения количества движения. Пусть v₀ – скорость шара с массой m до столкновения, v₂ – скорость этого же шара после удара, v₁ – скорость шара с массой M после столкновения. Тогда

mv₀ = Mv₁ + mv₂ или в проекциях на ось Х: mv_0х = Mv_1х + mv_{2 х}. Если ось направить в сторону v₀, то после нахождения проекций, будем иметь:

mv₀ = Mv₁ − mv₂. (1)

Считая систему консервативной, применим к ней закон сохранения полной механической энергии:

= + . (2)

Выразим v₀ из (1) и подставим в уравнение (2). После несложных преобразований найдем связь между v₁ и v₂. Вы должны получить: v₂ = v₁ .

Очевидно, что шар с массой m догонит шар с массой M, если

v₂ > v₁, то есть > 1 или > 3.

При решении этой задачи я уже подробно не останавливался на вопросе о том, почему данную систему можно считать замкнутой и консервативной. Если Вы внимательно изучили решения предыдущих задач на законы сохранения и изменения импульса и энергии, то такой вопрос перед Вами стоять не должен.

Ответ: > 3.

Задача 12. На гладкой горизонтальной поверхности на некотором расстоянии от вертикальной стенки покоится шар массы М = 0,8 кг. Другой шар, масса которого m = 0,2 кг, скользит с некоторой скоростью по направлению от стенки к первому шару. Между шарами происходит центральный и упругий удар в точке, находящейся на расстоянии L = 3 м от стенки. Второй шар после удара достигает стенки и, упруго отразившись от нее, догоняет и вторично ударяет первый шар. Определить, на каком расстоянии S от стенки произойдет второе соударение. Размерами шаров пренебречь.

Дано: L =3, М = 0,8 кг, m = 0,2 кг.

S − ?

Решение.

Воспользуемся решением и обозначениями предыдущей задачи. Итак, после первого соударения

v₂ = v₁ .

Чтобы решение стало немного проще, сразу вместо M и m подставим их числовые значения. В результате получим: v₂ = v₁.

Между первым и вторым ударами пройдет какое-то время ∆t. За это время первый шар (с массой М) успеет пройти расстояние S – L. Время, которое он на это затратит ∆t = .

За то же самое время второй шар успевает после отскока от первого шара вернуться к стенке (при этом он проходит путь L – d, где d – диаметр шара), отразиться от нее (это происходит мгновенно), добраться от стенки до точки первого столкновения (при этом он пройдет тот же путь L – d) и, в конце концов, вторично столкнуться с первым шаром (пройдя еще расстояние между первым и вторым ударами, равное S – L). Итак, за время ∆t второй шар успевает пройти путь, равный 2(L – d) + (S – L) = S + L – 2d (см. рисунок).

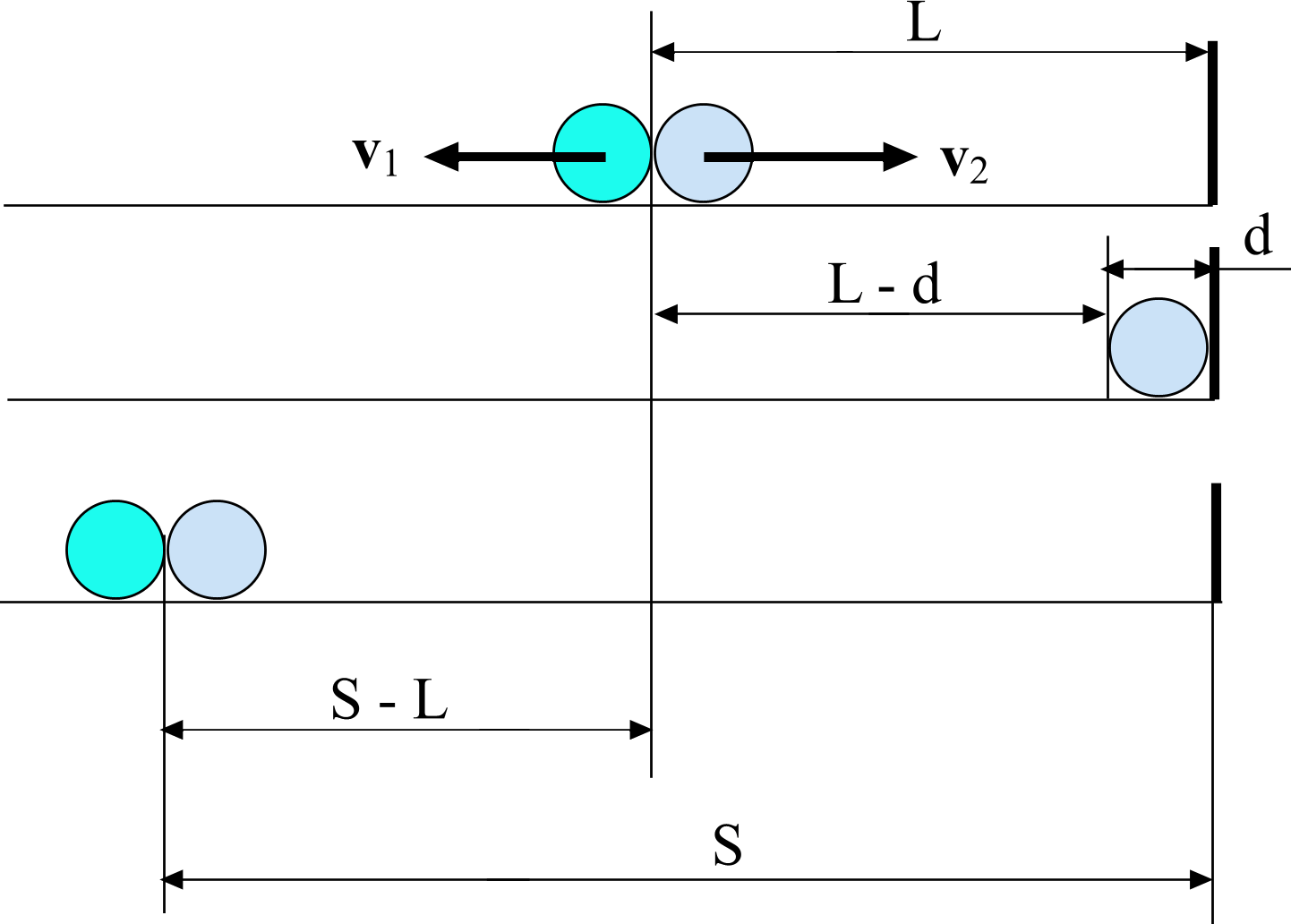
Если пренебречь размером шара (как и предлагает условие задачи), то путь, пройденный вторым шаром между двумя соударениями с первым, равен S + L. Поскольку величина скорости второго шара не изменилась при его ударе о стенку (удар упругий), то время, которое он затратит на прохождение пути S + L будет равно ∆t = .

Следовательно, = . Учитывая, что v₂ = v₁, получим: = .

Отсюда легко находим S:

S = 5L = 15 м.

Ответ: S = 15 м.

Задача 13. В неподвижный первый шар ударяет боком (не по линии, соединяющей центры шаров) второй шар такой же массы. Под каким углом разлетятся шары, если они однородные, абсолютно упругие и абсолютно гладкие?

Решение.

Пусть v₀ – скорость второго шара непосредственно перед столкновением, v₂ – скорость этого же шара после удара, v₁ – скорость первого шара после столкновения, m – масса каждого шара.

Разложим v₀ – по двум направлениям. Тогда можно считать, что за мгновение перед столкновением второй шар одновременно движется по некоторому направлению со скоростью v₂ и по какому-то другому направлению со скоростью . Что это за направления?

Вообще-то мы можем разложить v₀ по каким угодно направлениям, и в любом случае будет выполняться равенство v₀ = + v_2. Но, если не проходит через центр первого шара, то мы фактически вернемся к началу решения. Действительно, мы и начали с того, что второй шар движется со скоростью, направленной не по линии, соединяющей центры шаров. Лишь разложение v₀ по направлениям, одно из которых совпадает с линией, соединяющей эти центры, приблизит нас к решению задачи. Почему?

В этом случае в направлении происходит центральный удар. При этом, как известно, если массы шаров равны, то второй шар потеряет свою скорость в этом направлении, а первый шар приобретет в этом же направлении скорость v₁, причем v₁ = . Тогда после столкновения у второго шара останется только одна составляющая, а именно v₂.

Рассмотрим систему, состоящую из шаров в двух состояниях: непосредственно перед столкновением (рисунок слева) и сразу после удара (рисунок справа).

Считая систему замкнутой и консервативной, применим к ней закон сохранения количества движения и полной механической энергии.

В соответствии с законом сохранения импульса mv₀ = mv₁ + mv₂ или

v₀ = v₁ + v₂ (1)

В соответствии с законом сохранения энергии = + или

= + (2)

Возведем в квадрат обе части уравнения (1):

= + 2v₁v₂ + или

= + 2v₁v₂ Cos α+ , где α – искомый угол, то есть угол между v₁ и v₂.

Сравнивая последнее уравнение с уравнением (2), делаем вывод, что

2v₁v₂ Cos α = 0. Велична v₁ нулю не равна (первый шар в результате соударения приобрел энергию). Величина v₂ также не равна нулю, поскольку удар не является центральным. Получается, что Cos α = 0. Тогда α = 90⁰.

Ответ: α = 90⁰.

Задача 14. Первая частица массой m, движущаяся со скоростью v, налетает на вторую покоящуюся частицу массой m/2 и после упругого соударения отскакивает от нее под углом α = 30⁰ к направлению своего первоначального движения. С какой скоростью v₂ начнет двигаться вторая частица? Какова величина скорости v₁ первой частицы после столкновения? Движения частиц происходят в горизонтальной плоскости.

Дано: m, v, m/2, α = 30⁰.

v₂ − ? v₁ − ?

Решение.

Считая систему, состоящую из двух взаимодействующих частиц замкнутой и консервативной, применим к ней законы сохранения импульса и механической энергии.

Закон сохранения импульса: mv = mv₁ + или v = v₁ + .

Закон сохранения механической энергии: = + или

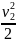v² = + . (1)

При записи закона сохранения механической энергии учтено, что взаимодействие происходит в горизонтальной плоскости, то есть изменение потенциальной энергии системы не происходит.

Спроектируем уравнение закона сохранения импульса системы на координатные оси, направления которых показаны на рисунке.

На ось Х: v = v₁ Cos α + . (2)

На ось Y: 0 = v₁ Sin α − . (3)

β – угол между направлением скорости v₂ второй частицы и осью Х.

Итак, мы имеем систему трех уравнений (1), (2) и (3) с тремя неизвестными (v₁, v₂ и β). Осталось всего-то решить эту систему, то есть найти неизвестные величины.

Как будем решать? Предложу один из вариантов (он, конечно, не единственный).

Запишем уравнения (2) и (3) иначе.

= v − v₁ Cos α,

= v₁ Sin α.

Теперь возведем в квадрат два последних уравнения. Для чего мы это делаем? Как Вы сейчас увидите, мы таким образом избавимся от одной неизвестной, а именно, от β. Итак,

= v² – 2vv₁ Cos α + Cos² α,

= Sin² α.

А теперь сложим эти два уравнения, не забывая при этом формулу «тригонометрической единицы». В результате сложения получим:

= v² – 2vv₁ Cos α +

Имеем уравнение с двумя неизвестными (v₁ и v₂.). Решим его совместно с уравнением (1). Для этого из (1) выразим и подставим в последнее уравнение.

= 2v² − 2 . Тогда = v² – 2vv₁ Cos α + или

− = v² – 2vv₁ Cos α + .

Выполнив простые преобразования и, учтя, что Cos α = Cos 30⁰ = , получим

3 − vv₁ + v² = 0. В результате имеем одно квадратное уравнение, из которого находим v₁.

v₁ = . Чтобы найти v₂, воспользуемся уравнением (1), из которого

v₂ = . Подставив сюда только что найденное выражение для v₁, получим:

v₂ = .

Осталось найти угол β, знание которого необходимо для определения направления v₂.

Угол β можно найти из уравнения (3).

Sin β = 2 Sin α.

С учетом найденных выражений для v₁ и v₂

Sin β = Sin α, то есть

β = α = 30⁰.

Ответ: v₂ = , β = 30⁰, v₁ = .

Задача 15. Пуля массой m, летящая горизонтально, попадает в деревянный брусок массой М, подвешенный на нити длиной L, и застревает в нем. На какой угол α отклонится брусок с пулей, если величина скорости пули равна v?

Дано: m, М, L, v.

α − ?

Решение.

Решение задачи выполним в неподвижной системе отсчета, связанной с Землей.

Рассмотрим систему, куда входят пуля и брусок, в трех состояниях. В первом состоянии брусок неподвижен, он вертикально висит на нити, а пуля со скоростью v уже подлетела к бруску (рисунок слева). Второе состояние соответствует моменту времени сразу после того, как пуля, попав в брусок, потеряла свою скорость (рисунок в центре). В третьем состоянии брусок (уже с пулей внутри) отклонен от вертикали на угол α, он неподвижен и «собирается» опускаться вниз (рисунок справа).

При переходе системы из первого состояния во второе закон сохранения механической энергии «не работает», поскольку в результате трения часть кинетической энергии пули переходит в тепло, количество которого нам неизвестно. А вот применить закон сохранения импульса мы можем, так как, во-первых, сила трения между пулей и бруском является внутренней по отношению к системе силой, а, во-вторых, для этого закона характер действующих сил (хоть внутренних, хоть внешних) вообще безразличен.

Что касается внешних сил, а именно силы, действующей на брусок с пулей со стороны нити и сил тяжести пули и бруска, то их действием можно пренебречь. Действительно, время перехода системы из первого состояния во второе (время движения пули внутри бруска) очень маленькое, и за это время скорость бруска (с пулей внутри) будет направлена по горизонтали. Внешние же силы в это время действуют по вертикали, и они не могут изменить общий импульс системы (да и импульс каждого тела системы) в горизонтальном направлении.

Пусть, после попадания пули в брусок, их совместная скорость равна u. Тогда закон сохранения импульса системы в проекциях на горизонтальную ось Х будет выглядеть так:

mv_х = (M + m) u_х. Очевидно, что направления v и u совпадают (удар неупругий). Если ось Х направить в сторону этих скоростей, то mv = (M + m) u, откуда

u = .

Теперь рассмотрим переход системы из второго состояния в третье с точки зрения возможности применения указанных законов. Конечно, закон сохранения импульса в этом случае не действует, так как во втором состоянии импульс системы равен (M + m) u, а в третьем состоянии он равен нулю (брусок с пулей остановился). Таким образом, произошло изменение импульса системы. Так может, применить закон изменения импульса? Можно, конечно, попробовать, но для этого мы должны знать время действия внешних сил, то есть время перехода системы из второго состояния в третье (время подъема бруска с пулей). Как найти это время? Для этого нужно воспользоваться кинематикой, применив кинематическое уравнение движения. Но каков вид этого уравнения? Мы его не знаем и найти его не так-то просто. Ведь система при переходе из второго состояния в третье движется под действием силы тяжести бруска с пулей и силы, действующей на систему со стороны нити (силы реакции нити). И, если первая из этих внешних сил все время остается постоянной как по величине так и по направлению, то о второй силе мы такого сказать не можем, поскольку ее направление постоянно меняется. Получается, что результирующая внешних сил является переменной величиной, следовательно, и ускорение системы будет с течением времени меняться, и применить уравнение движения с постоянным ускорением мы не можем.

Теперь рассмотрим ситуацию с точки зрения возможности применения закона сохранения механической энергии. Тут сразу возникает вопрос, а является ли наша система консервативной? То, что на систему действуют внешние силы, не является аргументом, чтобы считать систему неконсервативной. Другими словами, если система не является замкнутой, то это совсем не значит, что она неконсервативна. Напомню, что условиями консервативности системы являются равенство нулю алгебраической суммы работ всех внешних сил, действующих на систему, и отсутствие перехода механической энергии в другие виды энергии. Что касается последнего, то здесь все нормально: никакого преобразования механической энергии в другие виды энергии не происходит. Это при переходе системы из первого состояние во второе был такой «грех», потому-то мы тогда и «работали» с импульсом, а не с энергией. Теперь – о первом условии консервативности. Работа силы реакции нити действительно равна нулю, так как эта сила всегда перпендикулярна перемещению бруска с пулей в течение всего времени его движения. А вот о работе силы тяжести мы этого сказать не можем: сила тяжести совершает работу при подъеме бруска. Таким образом, наша система не только не замкнута, но и неконсервативна. Что же делать? Отчаиваться не следует: у нас еще есть в запасе закон изменения механической энергии системы, и ничто не мешает нам его применить.

Итак, изменение механической энергии системы равно алгебраической сумме работ всех внешних сил. Вначале найдем изменение энергии. Во втором состоянии кинетическая энергия системы равна .

Она же будет являться и полной энергией системы в этом состоянии. В третьем состоянии брусок с пулей покоится (это только мгновенье спустя он начнет двигаться вниз).

Таким образом, в третьем состоянии полная энергия системы равна 0. Изменение энергии системы при ее переходе из второго состояния в третье равно

0 − = − .

Еще раз напоминаю, что в качестве системы мы выбрали брусок и пулю. Земля не входит в систему, поэтому ни о какой потенциальной энергии взаимодействия с Землей говорить не приходится.

Теперь займемся работой внешних сил. Как уже было сказано, работа силы реакции нити равна нулю. Работа силы тяжести при подъеме бруска с пулей на высоту h равна − gh. Тогда

= gh. (1)

Отсюда h = .

Теперь легко определить угол α. Из рисунка видно, что Cos α = = 1 − или Cos α = 1 − . Подставив сюда найденное ранее выражение для u, получим:

Cos α = 1 − . Зная косинус угла, легко найти и сам угол.

Кстати, можно было бы переход из второго состояния в третье рассматривать не для системы, в которую входили брусок и пуля, а для другой системы, которая состояла бы из бруска, пули и Земли. Ведь право выбора системы всегда остается за нами. В этом случае надо было бы рассматривать потенциальную энергию взаимодействия Земли и ящика с пулей, но о работе силы тяжести мы бы уже не говорили, поскольку сила тяжести уже была бы внутренней силой и, кроме того, – потенциальной, не вызывающей изменения механической энергии. В результате мы опять пришли бы к уравнению (1).

Ответ: Cos α = 1 − .

Задача 16. Два упругих шарика подвешены на тонких невесомых нитях так, что они находятся на одной высоте и соприкасаются. Первый шарик имеет массу m₁ и подвешен на нити, длина которой равна L₁. Второй шарик шарик имеет массу m₂ и подвешен на нити, длина которой равна L₂. Первый шарик отклоняют на угол α = 60⁰ и отпускают. Какие по величине скорости v₁ и v₂ будут иметь первый и второй шарики соответственно сразу после столкновения? На какую максимальную высоту h₁ поднимется первый шарик, и на какую максимальную высоту h₂ поднимется второй шарик после соударения? Найти углы α₁ и α₂ на которые отклонятся соответственно первый и второй шарики после столкновения.

Дано: m₁, L₁, m₂, L₂, α = 60⁰.

v₁ − ? v₂ − ? h₁ − ? h₂ − ? α₁− ? α₂− ?

Решение.

Найдем величину скорости v₀ первого шарика в момент его соударения со вторым. Для этого рассмотрим систему первый шарик – Земля в двух состояниях. Первое состояние соответствует моменту, когда шарик отклонен на угол α, а второе – за мгновенье до столкновения со вторым шариком. Считая систему консервативной, применим к ней закон сохранения механической энергии:

m₁gh = . Отсюда v₀ = . Из рисунка 1 видно, что h = L₁ – L₁Cos α. Поскольку Cos 60⁰ = , то h = . Тогда v₀ = .

Рис. 1

Теперь рассмотрим систему состоящую из двух шариков в двух состояниях. Первое состояние соответствует моменту непосредственно перед столкновением, а второе – сразу после удара.

Поскольку время столкновения очень маленькое, то v₀ , v₁ и v₂ направлены практически горизонтально.

Поскольку внешние силы (а это – силы тяжести шариков и силы реакции нитей) направлены вертикально, а в горизонтальном направлении на систему не действуют никакие силы, то общий импульс системы в горизонтальном направлении сохраняется. Тогда

m₁v_0x = m₁v_1x + m₂v_2x.

Пусть направление оси Х совпадает с направлением v₀. Очевидно, что скорость v₂ второго шарика будет направлена в ту же сторону. А вот о направлении скорости v₁ первого шарика после столкновения мы ничего сказать не можем: все зависит от соотношения масс шариков. Если масса первого шарика меньше массы второго, то он отскочит назад, а, если больше, то он будет двигаться в направлении v₀. Если массы равны, то первый шарик остановится, а второй будет двигаться со скоростью v₀ в направлении оси Х. Поэтому запись для проекции скорости первого шарика оставим, как есть, то есть v_1x. Итак,

m₁v₀ = m₁v_1x + m₂v₂. (1)

Теперь рассмотрим систему шарики – Земля в тех же состояниях. Система консервативна, поскольку силы тяжести шариков являются внутренними потенциальными силами, а внешние силы реакции нитей работы не совершают, так как они направлены перпендикулярно перемещениям шариков. Таким образом, к системе можно применить закон сохранения механической энергии при переходе системы из первого состояния во второе. Потенциальную энергию шариков на уровне их соударения будем считать равной нулю (условие нормировки).

= + или = + . Поскольку = , то последнее уравнение можно записать так:

= + . (2)

В результате мы имеем два уравнения (1) и (2) с двумя неизвестными v_1x и v₂ (величину v₀ мы уже нашли раньше). Из уравнения (1)

v_1x = v₀ − v₂. (3)

Подставив это выражение в уравнение (2), после простых преобразований найдем:

v₂ = . Так как v₀ = , то

v₂ = .

Подставив это выражение в (3), найдем

v_1x = .

Очевидно, что модуль этой скорости

v₁ = .

Теперь найдем максимальные высоты, до которых поднимутся шарики после столкновения.

Сначала рассмотрим систему первый шарик – Земля в двух состояниях. Первое состояние соответствует моменту сразу после столкновения (шарик приобрел скорость v₁). Второе состояние соответствует моменту, когда шарик поднялся на высоту h₁ и на мгновенье остановился. Применяем закон сохранения механической энергии при переходе системы из первого состояния во второе.

= m₁gh₁. Подставив сюда выражение для v₁, найдем

h₁ = .

Проведя аналогичные рассуждения для системы второй шарик – Земля, будем иметь:

= m₂gh₂. Подставив сюда выражение для v₂, найдем

h₂ = .

И в заключение найдем α₁ и α₂. Из рисунка 2 видно, что Cos α₁ = = 1 − ,

Cos α₂ = = 1 − . Рисунок сделан для случая, когда L₁ > L₂ и m₁ < m₂

(первый шарик в результате столкновения отскочил от второго).

Рис. 2

С учетом выражений для h₁ и h₂ окончательно будем иметь:

Cos α₁ = 1 − ,

Cos α₂ = 1 − .

Ответ: v₁ = , v₂ = , h₁ = , h₂ = ,

Cos α₁ = 1 − , Cos α₂ = 1 − .

Задача 17. Три шара с одинаковыми радиусами, но различными массами подвешены рядом на нитях одинаковой длины и соприкасаются. Шар массой m₁ отклоняют так, что он поднимается на высоту H, и отпускают. При каких массах m₂ и m₃ все три шара после соударения первого шара со вторым и второго с третьим будут иметь одинаковые импульсы? На какую высоту они поднимутся? Все соударения считать абсолютно упругими.

Дано: m₁, H.

m₂ − ? m₃ − ? h₁ − ? h₂ − ? h₃ − ?

Решение.

На рисунке слева показано исходное состояние шаров. В центре показано состояние шаров непосредственно перед тем, как отклоненный первый шар будет отпущен. Рисунок справа демонстрирует состояние отклоненных от вертикали шаров после удара.

Рассмотрим систему, состоящую из второго и третьего шаров в двух состояниях: непосредственно перед столкновением и сразу после него. Поскольку время взаимодействия очень мало, то скорости второго шара до и после столкновения с третьим, а также скорость третьего шара после столкновения со вторым будут направлены горизонтально. Кроме того, эти скорости будут направлены в одну сторону, поскольку импульсы этих тел после столкновения одинаковы, следовательно, импульсы равны не только по величине, но и одинаковы направлены. Так как на систему не действуют силы в горизонтальном направлении, то для этого направления справедлив закон сохранения импульса. При данных условиях его можно сразу записать в модульной форме.

p₂ = p + p,

где p₂ – модуль импульса второго тела до его соударения с третьим, p – модуль импульса второго тела после его соударения с третьим, а также модуль импульса третьего тела после его соударения со вторым. Итак, p₂ = 2p.

Теперь рассмотрим систему, состоящую так же из второго и третьего шаров и Земли. Считая эту систему консервативной, запишем для нее закон сохранения механической энергии. Пусть условие нормировки таково, что шары, висящие вертикально, обладают нулевой потенциальной энергией.

При коротком времени соударения шары практически не изменят своей нулевой потенциальной энергии при переходе из первого состояния системы во второе. Тогда

= + , где

v₂ – величина скорости второго шара в первом состоянии системы (непосредственно до удара), u₂ – величина скорости второго шара во втором состоянии системы (сразу после удара), u₃ – величина скорости третьего шара во втором состоянии системы.

Запишем последнее уравнение иначе:

= + . Но –

это квадрат модуля импульса второго шара перед его столкновением с третьим, то есть = = , – это квадрат модуля импульса второго шара после его столкновением с третьим, то есть = p², – это квадрат модуля импульса третьего шара после его столкновением со вторым, то есть опять же = p². Тогда закон сохранения механической энергии примет уже такой вид:

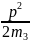= + . Отсюда легко находим: m₃ = .

Теперь рассмотрим систему, состоящую из первого и второго шаров в двух состояниях: непосредственно перед столкновением и сразу после него. Запишем для этой системы закон сохранения импульса. Пусть p₀ модуль импульса первого шара в первом состоянии системы (непосредственно перед соударением со вторым шаром). Мы знаем, что в этом состоянии системы второй шар покоился, то есть его импульс равен нулю. Сразу же после столкновения модуль импульса первого шара стал равен p (в соответствии с условием задачи), а модуль импульса второго шара стал равен 2p (мы это уже выяснили). Тогда

p₀ = p + 2p = 3p.

Далее рассматриваем систему, состоящую из первого и второго шаров и Земли в тех же двух состояниях и применяем к ней закон сохранения механической энергии. Запишем сразу этот закон через модули импульсов, как мы уже делали, когда применяли этот закон для системы: второй и третий шары – Земля.

= + . Отсюда легко находим: m₂ = . Тогда m₃ = .

Найдем высоты, на которые поднялись шары после рассмотренных соударений. Вначале займемся первым шаром. Рассмотрим систему первый шар – Земля в двух состояниях: в первом состоянии шар поднят на высоту Н, во втором состоянии первый шар подлетел ко второму (но еще не ударил).

Запишем закон сохранения механической энергии при переходе системы из первого состояния во второе (кинетическую энергию первого шара непосредственно перед его соударением со вторым представим так же, как и раньше, через модули импульсов).

m₁gH = . Выразим отсюда p² (понадобится в дальнейшем):

p² = gH.

Теперь для этой же системы запишем закон сохранения механической энергии, но рассмотрим систему уже в других двух состояниях. Первое состояние соответствует моменту сразу после соударения со вторым шаром, а во втором состоянии первый шар находится на высоте h₁. Имеем:

= m₁gh₁. Подставляем сюда найденное выражение для p² и, решая полученное уравнение, находим: h₁ = .

Теперь займемся вторым шаром. Рассматриваем систему второй шар – Земля. В первом состоянии системы второй шар находится сразу после соударения с третьим (модуль его импульса равен p). Во втором состоянии этот шар находится на высоте h₂. Применяем закон сохранения механической энергии при переходе системы из первого состояния во второе.

= m₂gh₂.

Подставляя сюда выражение для p² (p² = gH) и для m₂ (m₂ = m₁/2), находим:

h₂ = .

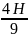И, наконец, − третий шар. Рассматриваем систему третий шар – Земля. В первом состоянии системы третий шар находится сразу после соударения со вторым (модуль его импульса равен p). Во втором состоянии этот шар находится на высоте h₃. Применяем закон сохранения механической энергии при переходе системы из первого состояния во второе.

= m₃gh₂.

Подставляя сюда выражение для p² (p² = gH) и для m₃ (m₃ = m₁/6), находим:

h₃ = 4H.

Ответ: m₂ = , m₃ = , h₁ = , h₂ = , h₃ = 4H.

Задача 18. Прикрепленный к вертикальной пружине груз медленно опускают до положения равновесия. В этом положении длина пружины оказывается на ∆L больше первоначальной. На какую максимальную величину ∆L₁ растянется пружина, если тому же грузу предоставить возможность свободно падать с такого положения, при котором пружина не растянута? Массой пружины и трением пренебречь.

Дано: ∆L.

∆L₁ − ?

Решение.

В положении равновесия на груз действуют две силы: сила тяжести груза, направленная вертикально вниз и равная по величине mg, а также сила реакции пружины, которая направлена вертикально вверх и равна по величине k ∆L, где k – жесткость пужины.

Поскольку груз неподвижен, то mg = k ∆L. Отсюда находим жесткость пружины, которая в дальнейшем понадобится при решении задачи.

k = .

Рассмотрим систему пружина – груз – Земля в двух состояниях: сразу после того, как груз подвесили к пружине и отпустили, давая ему возможность свободно падать, и в момент, когда груз растянул пружину на величину ∆L₁ (в этот момент груз на мгновенье остановится, чтобы начать движение вверх, то есть приступить к колебаниям, но это уже другая история…).

Данная система консервативна, поэтому при переходе системы из первого состояния во второе, ее механическая энергия не изменяется.

Как в первом, так и во втором состояниях скорость тела равна нулю, поэтому равна нулю и его кинетическая энергия. Таким образом, в каждом из выбранных состояний система обладает только потенциальной энергией.

В первом состоянии потенциальная энергия пружины равна нулю (она еще не успела деформироваться), а потенциальная энергия тела равна mgh, где h – высота тела относительно уровня, где потенциальная энергия, согласно условию нормировки, равна нулю. Этот уровень мы выбираем произвольно. Будем считать, что нулевой потенциальной энергией груз обладает в том месте, где пружина окажется максимально растянутой при падении груза, то есть h = ∆L₁. Таким образом, в первом состоянии механическая энергия системы равна mg ∆L₁.

Во втором состоянии потенциальная энергия груза равна нулю (он как раз находится на нулевом уровне потенциальной энергии в соответствии с нашим условием нормировки), а потенциальная энергия пружины равна . Таким образом, механическая энергия системы во втором состоянии равна .

Тогда mg ∆L₁ = , откуда ∆L₁ = . Но k = . Следовательно, ∆L₁ = 2∆L.

Ответ: ∆L₁ = 2∆L.

Задача 19. На горизонтальной плоскости лежат два связанных нитью одинаковых бруска, между которыми расположена сжатая пружина. Нить пережигают, и бруски разъезжаются в разные стороны так, что расстояние между ними становится равным d. Чему равна потенциальная энергия U сжатой пружины? Масса каждого бруска равна m. Коэффициент трения между брусками и плоскостью k. Пружина не скреплена с брусками. Массой пружины пренебречь.

Дано: d, m, k.

U − ?

Решение.

Рассмотрим систему, состоящую из брусков и пружины в двух состояниях: до пережигания нити (рисунок сверху) и после того, как бруски, разъехавшись в разные стороны, остановились (рисунок снизу).

Механическая энергия при переходе системы из первого состояния во второе не сохраняется, так как на систему действуют внешние силы: силы реакции плоскости, силы тяжести и силы трения. Силы реакции плоскости и силы тяжести хоть и являются внешними, работы не производят, поскольку направлены перпендикулярно перемещениям брусков. А вот неконсервативные силы трения совершают работу, в результате чего бруски в конце-концов останавливаются. Таким образом, к данной системе мы можем применить только закон изменения механической энергии. Правда, можно еще воспользоваться законом изменения импульса, но, думаю, обойдемся без него. Итак, полная механическая энергия системы в первом состоянии – это потенциальная знергия U сжатой пружины (потенциальная энергия брусков на том уровне, на котором они находятся, равна нулю – таково наше условие нормировки).

Во втором состоянии полная механическая энергия системы равна нулю (пружина распрямилась, бруски остановились). Изменение энергии системы при переходе ее из первого состояния во второе равно 0 – U = – U.

Рассмотрим работу сил трения. Работа силы трения при перемещении одного из брусков (любого) А₁ = − kmg r₁, где r₁ – модуль перемещения бруска при переходе системы из первого состояния во второе. (Формулу не комментирую, так как задачи на работу силы трения мы уже решали).

Работа силы трения при перемещении другого бруска А₂ = − kmg r₂. Очевидно (см. рисунок), r₁ = r₂ = − , где L – расстояние между брусками в первом состоянии системы.

Полная работа сил трения над системой А = А₁ + А₂ = − kmg (r₁ + r₂) или

А = − kmg d. Итак, закон изменения механической энергии системы будет выглядеть так:

– U = − kmg d, то есть энергия сжатой пружины равна U = kmg d.

Ответ: U = kmg d.

Задача 20. Легкая пружина, жесткость которой равна k, а длина L, стоит вертикально на столе. С высоты Н над столом на нее падает небольшой шарик, масса которого равна m. Какую максимальную скорость v_max будет иметь шарик при своем движении вниз? Трением пренебречь.

Дано: k, L, Н, m.

v_max − ?

Решение.

Проанализируем сценарий задачи. Во время падения шарика до пружины на него действует только сила тяжести со стороны Земли (сопротивлением воздуха пренебрегаем). Следовательно, скорость шарика постоянно увеличивается. Когда шарик коснулся пружины, его дальнейшее движение сопровождается действием уже двух сил: силы тяжести и силы реакции пружины (упругой силы). Причем последняя сила по мере сжатия пружины линейно возрастает по величине. Поскольку упругая сила направлена противоположно силе тяжести, то величина результирующей силы, действующей на шарик, будет меньше силы тяжести, и по мере сжатия пружины будет все более и более уменьшаться. Тем не менее, эта результирующая сила направлена вертикально вниз и придает шарику ускорение, хотя уже и меньшее, чем при отсутствии упругой силы. И скорость шарика продолжает увеличиваться по величине. Однако, в конце концов, пружина сожмется настолько, что сила упругости сравняется по величине с силой тяжести шарика, и результирующая сила станет равной нулю. А это значит, что в этот момент шарик лишается ускорения, и дальнейшее увеличение скорости при движении шарика вниз больше происходить не будет. Именно в этот момент скорость шарика и будет максимальной.

Поскольку величина упругой силы пропорциональна деформации пружины, то в этот момент mg = k ∆x₀, где ∆x₀ – это и есть величина деформации пружины, когда скорость шарика приняла свое максимальное значение.

Теперь приступим к решению. Рассмотрим систему состоящую из шарика, пружины (см. рисунок) и Земли.

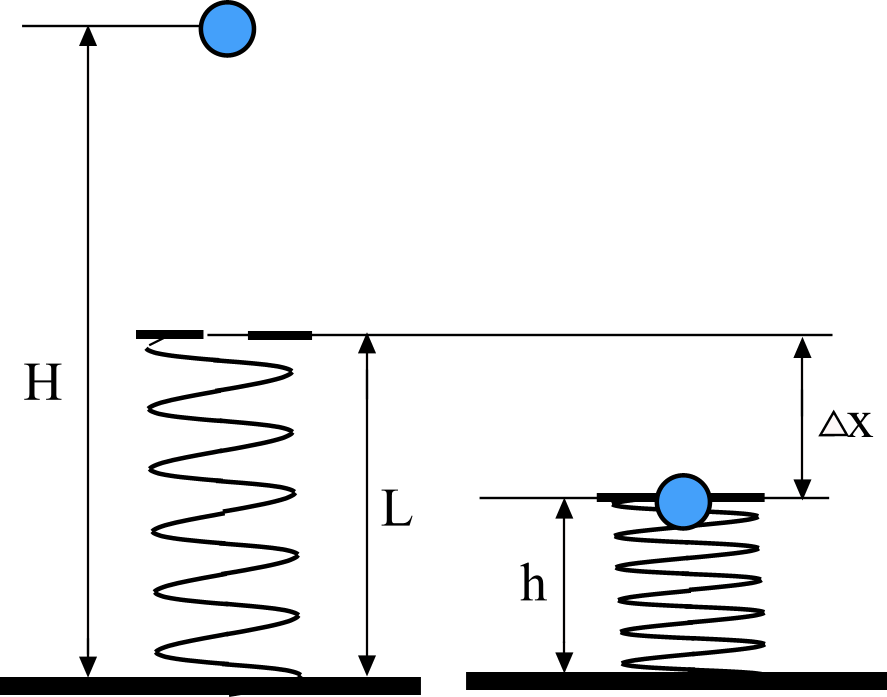
Выберем два состояния этой системы. Первое состояние соответствует моменту, когда шарик находится на высоте H. Второе состояние соответствует какому-то моменту времени, когда под действием шарика пружина деформирована на какую-то произвольную величину ∆х (неважно, какую). Считая систему консервативной, применим к ней закон сохранения механической энергии. Условие нормировки – потенциальная энергия равна нулю на уровне основания пружины.

В первом состоянии энергия системы равна mgH. Во втором состоянии энергия системы складывается из кинетической энергии шарика , имеющего величину скорости v в данный момент времени, потенциальной энергии шарика (mgh), находящегося в этот момент времени на высоте h относительно основания пружины и потенциальной энергии самой пружины , сжатой на величину ∆x. Таким образом,

mgH = + mgh + .

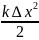Потенциальную энергию сжатой пружины представим в виде .

Как уже было сказано, максимальной скорости v_max шарик достигнет, когда

∆x = ∆x₀. В этом случае k ∆x₀ = mg. Или = m²g². Тогда потенциальная энергия пружины предстанет в виде , и закон сохранения механической энергии запишется так:

mgH = + mgh + .

Кроме того, как видно из рисунка, h = L − ∆x₀, а поскольку ∆x₀ = то

h = L − . Следовательно, mgH = + mg + . Отсюда после несложных преобразований

v_max = .

Ответ: v_max = .

Задача 21. Найти потенциальную энергию U системы, состоящей из двух одинаковых по размеру пружин, если под действием внешней силы система деформируется на величину ∆ℓ. Рассмотреть случаи, когда пружины соединены параллельно и последовательно (см. рисунок). Жесткости пружин k₁ и k₂. Массами пружин пренебречь.

Дано: ∆ℓ, k₁, k₂.

U − ?

Решение.

Вначале рассмотрим параллельное соединение пружин. В этом случае деформация каждой пружины имеет одну и ту же величину, равную деформации всей системы, то есть ∆ℓ = ∆ℓ₁ = ∆ℓ₂, где ∆ℓ₁ – деформация пружины с жесткостью k₁, ∆ℓ₂ – деформация пружины с жесткостью k₂. А вот про силы упругости, которые возникают в каждой пружине, этого сказать нельзя, поскольку при одинаковых деформациях жесткости пружин разные, а, значит, и сила упругости, равная произведению жесткости на деформацию, для каждой пружины своя.

Очевидно, что потенциальная энергия U системы складывается из потенциальной энергии U₁ пружины с жесткостью k₁ и потенциальной энергии U₂ пружины с жесткостью k₂, то есть U = U₁ + U₂.Но

U₁ = = ,

U₂ = = .

В свою очередь эту систему двух параллельных пружин мы можем мысленно заменить одной пружиной, эквивалентной данной системе. То есть эта воображаемая пружина будет деформироваться на такую же величину ∆ℓ, если к ней приложить ту же внешнюю силу. Пусть k_пар – жесткость этой эквивалентной пружины.

Тогда ее потенциальная энергия

U = . Тогда

= = , откуда следует, что жесткость эквивалентной пружины связана с жесткостями реальных пружин выражением k_пар = k₁ + k₂. Следовательно, U = .

Теперь рассмотрим последовательное соединение пружин. Также мысленно заменим эту систему одной эквивалентной пружиной с жесткостью k_пос. Теперь нашей задачей является нахождение связи между k_пос с жесткостями k₁ и k₂ реальных пружин.

В отличие от предыдущего случая, здесь деформация системы не равна деформации каждой пружины. В данном случае ∆ℓ = ∆ℓ₁ + ∆ℓ₂. Что же касается упругих сил, возникающих в пружинах, то они будут иметь одну и ту же величину в каждой пружине, поскольку при их последовательном соединении, каждую из них будет растягивать сила, равная по величине (да и по направлению) внешней силе. Пусть величина внешней силы F. Тогда для эквивалентной пружины

F = k_пос ∆ℓ, откуда ∆ℓ = .

Для пружины с жесткостью k₁

F = k₁ ∆ℓ₁, откуда ∆ℓ₁ = .

Для пружины с жесткостью k₂

F = k₂ ∆ℓ₂, откуда ∆ℓ₂ = .

Поскольку ∆ℓ = ∆ℓ₁ + ∆ℓ₂, то = + . Следовательно, = + . Отсюда

k_пос = . Следовательно, U = .

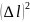Ответ: при параллельном соединении U = ,

при последовательном соединении U = .