Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский государственный педагогический университет им. Л.Н. Толстого

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Все сразу задачи с решениями для сайта.docx

Скачиваний:

Добавлен:

01.07.2025

Размер:

4.59 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

§ 12.3. Работа

Задача 1. Тело массы m находится на высоте h над поверхностью Земли. Найти работу А силы тяжести при движении тела с данной высоты до поверхности Земли, если: а) тело свободно падает; б) тело брошено вертикально вверх; в) тело брошено под углом к горизонту.

Дано: m, h.

А − ?

Решение.

Н а тело действует сила тяжести mg со стороны Земли. Поскольку сила постоянна, то ее работа определяется выражением А = mg∙Δr, где Δr – вектор перемещения тела.

а), б). В этих случаях тело совершает одно и то же перемещение Δr = АО (см. рисунок). Поэтому здесь сразу видно, что и работа в этих случаях будет одна и та же. Найдем ее.

По правилу вычисления скалярного произведения g∙Δr = g∙Δr∙Cos α, где

α – угол между направлениями g и Δr, Δr – модуль вектора перемещения Δr, то есть Δr = | Δr |. Поскольку α = 0, Δr = h, то А = mgh.

в). В этом случае Δr = АВ и g∙Δr = g∙Δr∙Cos β. Но Δr∙Cos β = АВ∙Cos β = h. Таким образом, и в этом случае А = mgh.

Следовательно, работа силы тяжести не зависит ни от скорости тела, ни от угла, под которым оно было брошено, а определяется для данного тела и данной местности только высотой поднятия тела над поверхностью Земли, то есть его положением.

Ответ: А = mgh.

Задача 2. Тело массы m брошено вертикально вверх с высоты h₁ над поверхностью Земли. Найти работу А силы тяжести при движении тела с данной высоты до высоты: а) h₂ > h₁; б) h₃ < h₁.

Дано: m, h₁, h₂, h₃.

А − ?

Р ешение.

Так же, как в предыдущей задаче А = mg∙Δr, где Δr – вектор перемещения тела.

а). В этом случае тело совершает перемещение Δr = АВ (см. рисунок). Поэтому g∙Δr = g∙АВ∙Cos α, где α – угол между направлениями g и АВ.

Поскольку α = 180⁰, Δr = АВ = h₂ – h₁ = Δh₁, то

А = − mg Δh₁.

б). В этом случае Δr = АС и g∙Δr = g∙АС∙Cos β, где β – угол между направлениями g и АС. Этот угол равен нулю, поэтому А = mg АС. Но АС = h₁ – h₃ (не наоборот, поскольку АС положительная величина, это – модуль вектора АС). Обозначим h₁ – h₃ = Δh₂. Тогда

А = mg Δh₂.

Таким образом, величина работы силы тяжести при перемещении тела с одной высоты на другую равна произведению массы тела на величину ускорения свободного падения и на разность высот (из большей высоты вычитают меньшую). Знак же самой работы зависит от угла между направлением вектора перемещения тела и направлением ускорения свободного падения. На практике же удобно не думать об этом угле, а при вычислении работы брать разность между начальной высотой тела и его конечной высотой. В этом случае нужный знак появится автоматически.

Так же, как и в предыдущей задаче, работа силы тяжести не зависит от траектории движения тела, а определяется его положением.

Ответ: а) А = − mg Δh₁; б) А = mg Δh₂.

Задача 3. Тело массы m брошено с поверхности Земли под углом α к горизонту со скоростью, величина которой v₀. Найти работу А силы тяжести при движении тела: а) от точки бросания до высоты максимального подъема; б) от точки бросания до точки падения тела на Землю.

Дано: m, v₀, α.

А − ?

Решение.

На тело действует сила тяжести mg со стороны Земли. Поскольку сила постоянна, то ее работа определяется выражением А = mg∙Δr, где Δr – вектор перемещения тела.

а ). В этом случае перемещение

Δr = ОА (см. рисунок).

Поэтому А = mg∙ОА.

Но g∙ОА = g∙ОА∙Cos β (напоминаю, что угол берется между направлениями векторов). В то же время

β = 180⁰ − γ, тогда

g∙ОА = − g∙ОА∙Cosγ. Но ОА∙Cosγ = H, где Н – высота максимального подъема. Следовательно,

g∙ОА = − gH, и А = − mgH.

Из кинематики известно, что Н = (см. решение задачи 11.2.13), поэтому

А = − mg = − m .

б). В этом случае перемещение Δr = ОВ (см. рисунок). Поэтому А = mg∙ОВ. Но g∙ОВ = g∙ОВ∙Cos 90⁰ = 0, следовательно, А = 0.

Ответ: а) А = − m ; б) А = 0.

Задача 4. Однородный стержень массой m и длиной L из вертикального положения падает на землю. Найти работу силы тяжести.

Дано: m, L.

А − ?

В предыдущих задачах было показано, что работа силы тяжести не зависит от формы траектории, по которой тело падает на землю (или поднимается), а определяется высотой нахождения тела над поверхностью земли. В данной задаче разные участки стержня находятся на разных высотах, поэтому нахождение работы силы тяжести при падении всего стержня как целого, требует применения специального приема. Этот мощный метод решения многих сложных задач основан на применении математической теории бесконечно малых величин (дифференциального и интегрального исчислений). Вообще-то суть этого метода проста, и эта задача будет являться примером его применения.

Мысленно «разрежем» горизонтальной плоскостью стоящий стержень на кусочки бесконечно малой высоты dℓ. Естественно, что таких кусочков по всей длине стержня получится огромное (бесконечное) количество. Это – операция дифференцирования, то есть разделения объекта на части. В нашем примере – на бесконечно малые части. Каждый такой кусочек обладает массой, бесконечно малой (элементарной) массой dm. Падение стержня как целого на землю есть совокупное падение всех его элементарных масс. Если мы найдем работу силы тяжести при падении каждого кусочка (она называется элементарной работой) и сложим все эти элементарные работы, то мы найдем работу силы тяжести при падении всего стержня. Понятно, что этих работ − бесконечное количество, но не переживайте, всю жизнь Вам их складывать не придется. Это сложение – операция интегрирования, и правила быстрого выполнения этой операции давно уже разработаны в соответствующем разделе математики. Как дифференцирование, так и интегрирование «проходятся» в школе. Сейчас мы применим эти знания на практике.

Выберем произвольный кусочек стержня, расположенный на расстоянии ℓ от его основания. Если обозначить площадь поперечного сечения стержня как S, то элементарный объем этого кусочка dv = S∙dℓ, а его элементарная масса

dm = ρ∙dv = ρS∙dℓ, где ρ – объемная плотность стержня. Поскольку ρ = , а объем всего стержня V = LS, то dm = .

Теперь можно найти элементарную работу dA силы тяжести при падении этого кусочка на землю с высоты ℓ: dA = ℓg∙dm = ℓg .

Настало время сложить все эти элементарные работы, то есть выполнить интегрирование и получить полную работу А. Это интегрирование следует выполнить по всей длине стержня, начиная от основания (ℓ = 0) и заканчивая «макушкой» стержня (ℓ = L). Итак, полная работа А = = . Постоянные величины (g, m, L) можно вынести за знак интеграла, тогда

А = . Интеграл, который необходимо решить (или, как говорят, «взять интеграл»), это − один из самых простых, так называемых, табличных интегралов, которые надо знать наизусть. = = . Тогда А = .

Чтобы поднять стержень, нужно выполнить такую же работу, только, понятно, другой какой-то (назовем ее внешней) силой: сила тяжести «умеет» только ронять.

Ответ: А = .

Задача 5. Однородную оконную штору массой m и длиной L свертывают в тонкий валик над окном. Какова наименьшая затрачиваемая при этом работа А_min?

Дано: m, L.

А_min − ?

Решение.

Эта задача интересна не особенностями математических приемов ее решения (в этом отношении она не отличается от предыдущей задачи), а корректным применением такого понятия как работа.

Предлагаю начать решение с постановки следующего вопроса, какова работа, совершенная силой тяжести шторы при ее поднятии? Наверняка, кто-то скажет о том, что эта сила не может быть причиной поднятия шторки. Конечно, не может, но ведь никто этого и не утверждал, а было просто скромно предложено найти работу этой силы. Кстати, может быть триста двадцать пять миллионов причин того, что шторка оказалась поднятой вверх. Не будем анализировать эти причины, а сфокусируем внимание на вопросе задачи. Что, собственно, от нас хотят? Хотят, чтобы была найдена «наименьшая работа». Работа чего? И вот тут Вы должны знать, что в механике есть понятие работа силы. Убедительно прошу Вас выбросить раз и навсегда из головы такие понятия как «работа против силы», «работа тела» (например, работа ветра), «работа против тела» и т. д. Таких понятий в механике нет. А, если Вы их будете использовать, то только запутаетесь и в теории, и, тем более, в решениях задач.

Если на тело действует сила, и при этом тело совершает перемещение, то эта сила совершает работу. И все! Других мнений быть не должно. И никого не интересует, под действием этой ли силы совершено данное перемещение, или шторка поднялась в результате действия тех миллионов причин, о которых говорилось выше. Неважно. Есть перемещение, есть сила тяжести шторки, и я имею право поставить и решить вопрос о работе этой силы.

И еще. Забегая вперед, скажу, что эта работа будет отрицательна. И в этом нет ничего плохого и ничего хорошего. Просто так есть и все. Я об этом говорю потому, что, возьми любую книгу по физике, и почти наверняка где-нибудь Вы натолкнетесь на то, что автор терпеливо объясняет физические причины возникновения отрицательного знака: «знак минус возник оттого, что…» или «знак минус говорит о том, что…». Вы где-нибудь встречали такое же подробное физическое объяснение возникновения знака «плюс»? Практически никогда и нигде! Чем же минус «хуже» плюса?

Почему авторы, как бы конфузясь, начинают быстренько «оправдываться» в том, что недосмотрели, дескать, извините, но, уж раз он появился, проклятый, то приходится объяснять, откуда он взялся.

Ничего объяснять не надо. Ни плюса, ни минуса. Они в равной степени «имеют право на существование». Если вычисление работы будет сделано математически грамотно, то нужный знак автоматически появится сам собой. Другое дело, когда какая-нибудь величина по своему существу не может быть отрицательной в рамках данной теории, например, масса, путь, вектор, модуль вектора. Вот тут действительно надо задуматься, и объяснить всем, почему у тебя, например, получилась отрицательная масса.

Кстати, именно в подобных случаях авторы часто скромно помалкивают и говорят, например, нисколько не смущаясь: «тело движется с ускорением

а = − 5 м/с²» или «путь тела изменяется по закону s = 5 – 10 t²». Разве Вы не встречали подобного? И ведь многие «проглатывают» эту неряшливость и почему-то не задумываются над тем, что модуль ускорения не может быть отрицательным, а путь не может изменяться по приведенному выше закону, потому что при некоторых значениях времени он становится отрицательным. Но стоит только появиться перед работой отрицательному знаку, как все дружно на него набрасываются и начинают что-то объяснять. А работа – это скаляр, и ему сам Бог велел быть или положительным или отрицательным.

Но, вернемся к нашей шторке. Выделим мысленно кусочек шторки с элементарной массой dm на каком-то произвольном расстоянии ℓ от подоконника.

О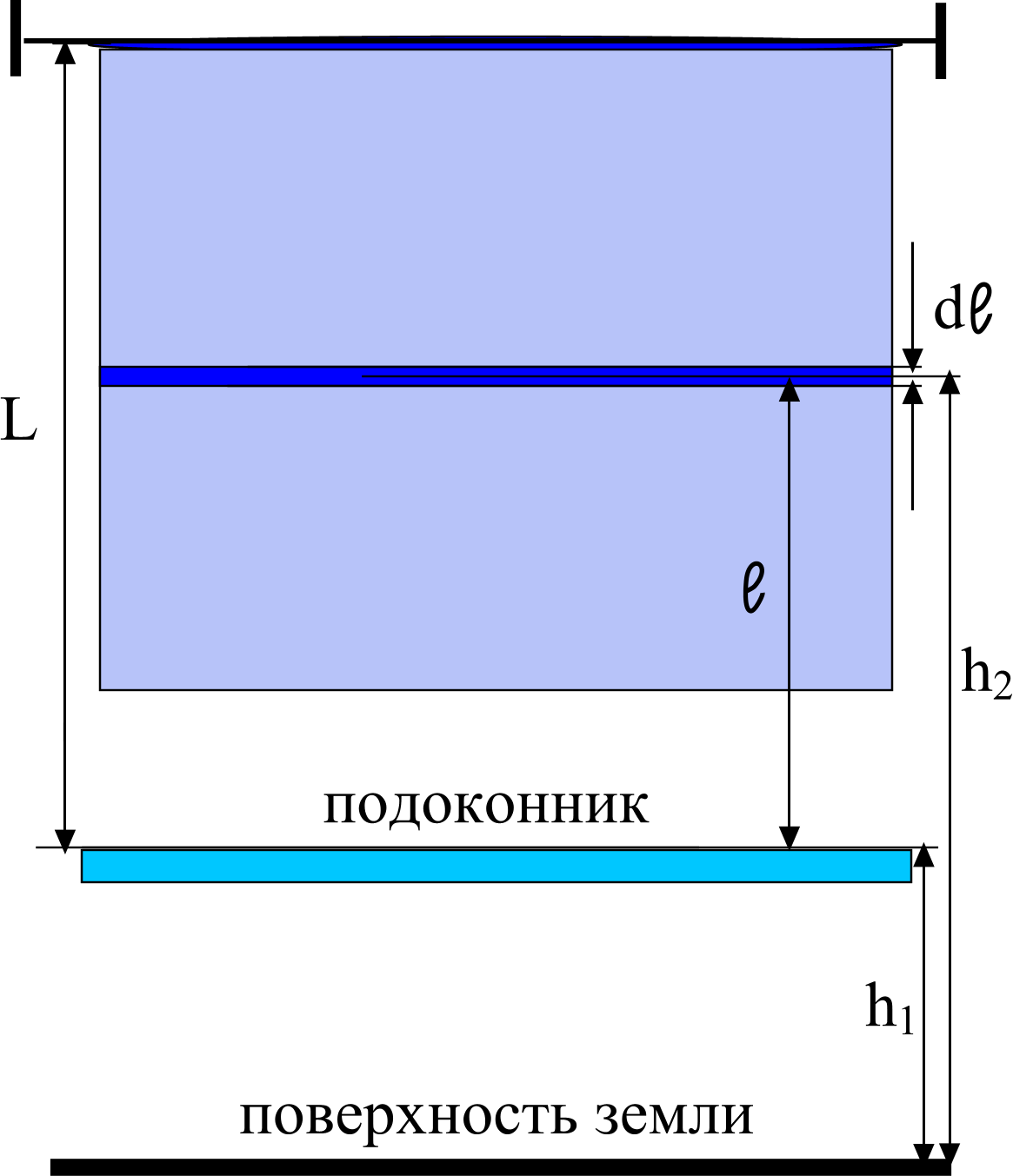 чевидно, что ℓ = h₂ – h₁, где h₁ – высота подоконника над землей, а h₂ – высота расположения выделенного участка шторки тоже относительно поверхности земли (см. рисунок). Если обозначить площадь поперечного сечения шторы как S, то элементарный объем этого кусочка dv = S∙dℓ, а его элементарная масса

dm = ρ∙dv = ρS∙dℓ, где ρ – объемная плотность шторы. Поскольку ρ = , а объем всей шторы V = LS, то dm = .

Теперь можно найти элементарную работу dA силы тяжести при поднятии выделенного кусочка шторы с высоты h₁ до высоты h₂ над поверхностью земли, то есть при его перемещении на расстояние ℓ: dA = − ℓg∙dm = − ℓg . После этого находим полную работу А. Для этого следует взять интеграл от последнего выражения. Интегрирование следует выполнить по всей длине шторки, начиная от подоконника (ℓ = 0) и заканчивая верхним положением шторки, когда она уже будет свернута в тонкий валик (ℓ = L).

Итак, полная работа А = = . Постоянные величины (g, m, L) можно вынести за знак интеграла, тогда А = − . Этот интеграл мы уже рассматривали в предыдущей задаче. Получаем А = − .

Конечно, шторка сама себя не поднимет. Для этого к ней нужно приложить какую-то силу со стороны. Зачем же мы тогда вычисляли работу силы тяжести? Дело в том, что нас интересует минимальная работа внешней силы, поэтому мы должны оценить ее величину. Поскольку и сила тяжести, и внешняя сила совершают работы при одной и той же величине перемещения шторы, то напрашивается вывод, что внешняя сила должна быть по величине равна силе тяжести.

Меньше она быть не может, в противном случае равнодействующая двух этих сил будет направлена в сторону силы тяжести. У внешней силы просто «не хватит силы» (простите за тавтологию) поднять шторку. А может ли внешняя сила быть больше силы тяжести? Конечно, может. В этом случае шторка, безусловно, будет поднята, правда, работа такой силы уже не будет минимальной, да и двигаться штора будет вверх с ускорением, глядишь, и сломает чего-нибудь при своем полном подъеме.

Поскольку при подъеме шторки ее сила тяжести постоянно меняется (точнее, той ее части, которая еще висит), то для обеспечения условия задачи (чтобы работа была минимальной) необходимо, чтобы и внешняя сила изменялась бы по такому же закону.

Направление внешней силы совпадает с перемещением шторки, поэтому работа этой силы положительна. Таким образом, А_min = .

Ответ: А_min = .

Задача 6. Тело массы m вращается на горизонтальной поверхности по окружности радиуса r. Найти работу силы трения при повороте тела на угол α. Коэффициент трения между телом и поверхностью равен k.

Дано: m, r, k.

А − ?

Решение.

Поскольку тело движется только в горизонтальной плоскости, его сила тяжести и сила нормальной реакции плоскости равны по величине. Следовательно, величина силы трения F_тр = kmg.

При повороте тела на угол α оно совершит перемещение Δr, однако, работа А силы трения не может быть найдена по формуле А = F_тр∙Δr. Дело в том, F_тр – переменная величина и на перемещении Δr она, оставаясь неизменной по величине, постоянно меняет свое направление.

Д ля решения задачи поступим следующим образом. Мысленно разобьем траекторию тела, по которой оно двигалось при повороте на угол α, на бесконечно малые кусочки, и рассмотрим движение тела в пределах одного из этих кусочков. Другими словами, рассмотрим движение тела в течение бесконечно малого промежутка времени dt, в пределах которого тело повернулось на элементарный угол dα, совершив при этом элементарное перемещение dr. Тогда, имея в виду, что в течение элементарного отрезка времени dt сила трения остается практически постоянной, найдем ее элементарную работу на перемещении dr: dА = F_тр∙dr. Сила трения всегда направлена противоположно скорости, а скорость и dr совпадают по направлению (являются касательными к траектории). Следовательно, угол между F_тр и dr равен 180⁰. Тогда dА = − F_тр∙dr, где dr – модуль вектора dr, то есть dr = | dr |. Из определения угла (в радианах) мы имеем dα = , где ds – элементарная дуга окружности. Но ds = dr, тогда dα = , откуда dr = r∙dα. Следовательно,

dА = − F_тр∙r∙dα. Полную работу силы трения при движении тела в пределах угла α найдем, взяв интеграл от последнего выражения. Интеграл следует брать в пределах от 0 до α.

Итак, А = = − 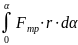. Величины F_тр и r выносим за знак интеграла как постоянные величины.

Тогда А = − F_тр∙r∙ = − F_тр∙r∙α = − kmg∙r∙α.

Кстати, r∙α – это длина дуги, по которой двигалось тело при повороте на угол α, то есть путь, пройденный телом при этом повороте.

Ответ: А = − kmg∙r∙α.

Задача 7. Какую минимальную работу А_min нужно совершить, чтобы однородную доску длиной L и массой m повернуть в горизонтальной плоскости вокруг одного из концов на угол α? Коэффициент трения между доской и землей равен k.

Дано: L, m, α, k.

А_min − ?

Решение.

Очевидно, эта работа равна по величине работе силы трения, действующей на доску при ее вращении (аналогичная ситуация рассматривалась в решении предыдущей задачи). Сила трения в данном случае является величиной переменной, поэтому для нахождения ее работы применим обычный метод дифференцирования и интегрирования.

Мысленно разбиваем доску на участки элементарной длины dℓ. Я уже не буду подробно показывать, как находится элементарная масса (если забыли, вернитесь к задачам 12.3.4 или 12.3.5). Элементарная масса dm = dℓ. Величина силы трения, действующей на элемент доски dF_тр = kg∙dm = kg∙ . Если этот элемент находится на каком- то (произвольном) расстоянии ℓ от неподвижного конца, то сила трения, действующая на этот элемент, совершит элементарную работу

dA = − dF_тр∙ℓ∙α (см. предыдущую задачу) или

dA = − kg∙ ∙ℓ∙α.

Полную работу силы трения найдем интегрированием последнего выражения в пределах длины всей доски, то есть от 0 до L.

А = − = − . Окончательно

А = − .

Такую же по величине работу необходимо совершить и внешней силе, чтобы повернуть доску на угол α. Только работа эта будет положительна: А_min = .

Кстати, α·L – это длина дуги, по которой двигались самые дальние от центра вращения точки доски при ее повороте на угол α, то есть путь, пройденный каждой из этих точек при таком повороте.

Ответ: А_min = .

Задача 8. Санки, массы m, движущиеся по горизонтальному льду, выезжают на горизонтальный асфальт. Проехав по асфальту расстояние L, равное длине полозьев, санки остановились. Найти работу А силы трения, если коэффициент трения санок об асфальт k₁, о лед k₂.

Дано: m, L, k₁, k₂.

А − ?

Решение.

Начиная с момента, когда сани выехали со льда на асфальт, на них будет действовать переменная сила трения. Действительно, величина силы трения определяется произведением коэффициента трения на величину силы нормальной реакции поверхности, по которой едут сани. Поскольку движение происходит по горизонтали, то величина силы нормальной реакции равна величине силы тяжести саней. Однако одна часть саней движется по льду, а другая – по асфальту. И, если соответствующие коэффициенты трения не изменяются в процессе движения саней, то изменяются массы частей саней, движущихся и по асфальту и по льду. Часть массы саней, которая движется по асфальту, все время увеличивается от нуля до полной массы саней, другая же часть, которая все еще продолжает свое движение по льду, уменьшает свою массу от m до нуля. Все это и является причиной движения саней с переменной силой трения.

Рассмотрим элемент dℓ саней с элементарной массой dm, совершившей перемещение ℓ в сторону асфальта, от границы, разделяющей асфальт и лед.

Элементарная работа силы трения при этом dA₁ = − dF_тр1∙ℓ, где dF_тр1 – сила трения между асфальтом и выделенным элементом саней.

Поскольку dF_тр1 = k₁gdm, а dm = dℓ, то dF_тр1 = k₁g dℓ.

Следовательно, dA₁ = − k₁g ℓ dℓ. Полная работа силы трения при движении саней по асфальту A₁ = − k₁g = −

Проведя подобные рассуждения, найдем работу А₂ силы трения при движении саней по льду: A₂ = − . Полная работа А = А₁ + А₂ = − (k₁ + k₂).

Ответ: А = − (k₁ + k₂).

Задача 9. Две материальные точки, массы которых M и m в начальный момент времени находятся на бесконечно большом расстоянии одна от другой. В результате гравитационного притяжения материальные точки начинают сближаться. Найти работу гравитационной силы: а) за время от начала сближения до момента, когда расстояние между точками стало равно r₁; б) за время, когда расстояние между точками уменьшится от r₁ до r₂.

Дано: M, m, r₁, r₂.

А − ?

Решение.

Рассмотрим взаимодействие точек в системе отсчета, связанной с точкой, масса которой M. Назовем ее первой точкой, с ней же свяжем и начало системы. В этой системе отсчета первая точка неподвижна, а вторая движется к ней под действием силы притяжения, величина которой F = γ , где γ – гравитационная постоянная, r – расстояние между материальными точками.

При решении этой задачи мы встречаемся с двумя трудностями. Во-первых, гравитационная сила меняется по величине по мере движения второго тела в сторону первого. Однако это не должно нас сильно беспокоить: мы уже знаем, каким методом нужно пользоваться для нахождения работы переменной силы.

Во-вторых, гравитационная сила «не привязана» к системе отсчета. Что имеется в виду? Гравитационная сила зависит от координат тела (его радиус-вектора). Координаты же одного и того же тела разные в разных системах отсчета, значит, и формула зависимости силы от координат будет разной в разных системах отсчета. Вы можете сказать, что знаете только одну формулу для гравитационной силы (ту, что приведена выше), и ее выражение одно и то же, в какой бы системе отсчета ни находились взаимодействующие тела. Это не так. Конечно, данная формула выглядит одинаково в любых системах отсчета, но ведь это не формула гравитационной силы! А что же это тогда такое? Это формула для подсчета модуля этой силы. Ведь, когда мы говорим сила, то имеем в виду вектор. Вектор и его модуль – это совершенно разные вещи. Понятно, почему выражение для модуля гравитационной силы одинаково в любой системе отсчета: в эту формулу входят инварианты, то есть величины, не изменяющиеся при переходе из одной системы отсчета в другую. Это − массы тел и расстояние между ними. В разных системах отсчета координаты тел разные, но расстояние между ними – инвариант.

Про гравитационную постоянную говорить вообще не приходится, на то она и постоянная, чтобы везде быть одинаковой.

Итак, чтобы решить задачу, нам необходимо выбрать систему отсчета и «привязать» к ней силу взаимодействия между материальными точками. Предвижу вопрос о том, почему мы только сейчас «спохватились», а не делали этой «привязки» ранее, ведь столько уже задач на динамику решили. И сила, зависящая от координат, встречалась (сила тяжести) и сила, зависящая от скорости, – тоже (сила трения). Дело в том, что в предыдущих задачах эта «привязка» тоже была, но она осуществлялась как бы сама по себе, автоматически, и специально акцентировать внимание на этом вопросе просто не было необходимости. Действительно, когда шла речь о силе тяжести, мы ее записывали как mg, а ускорение к данной системе отсчета уже «привязано»: ведь, например, проекции этого ускорения мы находим применительно к конкретной системе отсчета, в другой системе они были бы другими. Аналогично и с силой трения. Правда, подобная привязка к системе отсчета тут в явном виде в глаза не бросается, но мы ее направление сопоставляли с направлением скорости, и этого нам было достаточно, чтобы решать задачи.

Как же поступить в данном случае и связать направление гравитационной силы с выбранной системой отсчета? Все просто. Сначала нужно выбрать систему отсчета. Тело отсчета и начало системы мы уже выбрали (это – первая материальная точка). Осталось выбрать направление оси. Ось, конечно, будет одна (например, ось Х), и пусть она будет направлена от первой точки ко второй (см. рисунок). Вы знаете, что с каждой осью связан соответствующий орт. Обычно орты на рисунках показывать не принято, но в данном случае это будет полезно.

Вот теперь вектор силы можно представить так: F = − γ i, где i − орт оси Х. Противоположное направление F и i объясняет знак минус перед формулой. В литературе традиционно встречается другая форма записи вектора этой силы, а именно: F = − γ r. Легко видеть, что это практически то же самое, что и предыдущая формула. Действительно,

F = − γ r = − γ . Но – это единичный вектор радиус-вектора, по сути − тот же самый орт i (он и направлен туда же и модуль его равен единице). Не будем нарушать традиций и в дальнейшем отдадим предпочтение формуле

F = − γ r.

Элементарная работа гравитационной силы при бесконечно малом перемещении dr второго тела dA = − γ r∙dr.

В решении задачи 12.3.5 говорилось о том, что, если вычислять работу математически грамотно, то никаких проблем со знаком работы не возникнет, нужный знак появится автоматически и никакого физического объяснения, почему появился тот или иной знак, давать не нужно. О том, как в данном случае математически корректно выполнить вычисление работы, мы сейчас и поговорим. Прошу отнестись к этому с особым вниманием, в противном случае так и будете всю жизнь путаться с плюсами и минусами.

Что такое r∙dr? Это – скалярное произведение радиус-вектора второй материальной точки (или, что то же самое – точки приложения силы F) и вектора перемещения dr. Как вычисляется это произведение? Вот так: r∙dr = r∙dr·Cos α, где α – угол между направлениями векторов r и dr, dr – это модуль вектора dr, то есть dr = | dr |. В разделе Курса Векторная алгебра (см. задачу № 6) было показано, что r∙dr = r∙dr. Напомню, что в этой формуле dr – это уже изменение модуля вектора r, то есть dr = d| r |. Если что-то непонятно, обязательно вернитесь к Векторной алгебре.

После этого замечания, формула для элементарной работы примет вид:

dA = − γ r∙dr = − γ ∙dr, где dr – изменение модуля вектора r. Дальше – просто. Чтобы вычислить полную работу, надо взять интеграл от последнего выражения в пределах от r₀ (r₀ = до r₁.

а). А = = −γ Mm . Данный интеграл является табличным. = = − . Тогда А = γ − γ или А = γ так как

γ = 0, поскольку r₀ =

б). А = . Взяв интеграл, получим А = γ − γ или

А = γ Mm .

Обратите внимание, при вычислении полной работы мы брали интегралы в пределах либо от до r₁, либо от r₁ до r₂, но в любом случае речь идет о модулях радиус-векторов, а не о модуле вектора перемещения. Именно поэтому мы и выбрали ту форму записи для элементарной работы, куда входит изменение модуля радиус-вектора, а не модуль его изменения.

Ответ: а) А = γ ; б) А = γ Mm .

Задача 10. Имеется пружина, один конец которой закреплен. К другому концу приложена сила, действующая вдоль пружины и растягивающая ее. Когда величина упругой деформации достигла значения r₀, внешняя сила исчезла. Найти работу А_упр упругой силы при возвращении пружины в состояние равновесия из положения, когда ее деформация была равна r₀ до положения, когда ее деформация растяжения стала r₁. Жесткость пружины равна k.

Дано: r₀, r₁, k.

А_упр − ?

Решение.

В начале определимся с системой отсчета. Пусть ее началом будет точка, совпадающая с незакрепленным концом недеформированной пружины. Направление оси Х выберем, как показано на рисунке. Такой выбор системы отсчета удобен тем, что в этом случае деформация пружины равна модулю радиус-вектора ее незакрепленного конца. Это немного упростит решение.

Пусть под действием упругой силы пружина перешла из состояния с деформацией r₀ в состояние с деформацией r₁. Поскольку изменение состояния пружины происходит в пределах упругих деформаций, то F₀ = − kr₀∙i, F₁ = − kr₁∙i, где i – орт оси Х. Вот мы и «привязали» силу упругости к выбранной системе отсчета.

При переходе пружины из одного состояния в другое, величина силы упругости постоянно меняется, следовательно, нам вновь придется применить метод исчисления бесконечно малых.

В пределах бесконечно малого перемещения dr сила практически остается постоянной. Тогда ее элементарная работа на этом перемещении

d А_упр = F∙dr = − kr∙dr.

Как Вы уже знаете, r∙dr = r∙dr, где dr – изменение модуля радиус-вектора при перемещении. Тогда dA = − kr∙dr. Теперь легко найти полную работу.

А_упр = − = − .

Ответ: А_упр = − .

Задача 11. Имеется пружина, один конец которой закреплен. К другому концу приложена внешняя сила, действующая вдоль пружины и растягивающая ее. Величина силы пропорциональна деформации пружины, жесткость пружины равна k. Найти работу А этой силы при растяжении пружины если: а) пружина растягивается из недеформированного состояния, до состояния, при котором величина деформации равна r₁; б) пружина растягивается из уже деформированного до величины r₁ состояния, до состояния, при котором величина общей деформации пружины равна r₂. Найти также работу упругой силы при этих же условиях.

Дано: r₁, r₂, k.

А − ? А_упр − ?

Решение.

Систему отсчета выберем также, как и в предыдущей задаче.

П усть под действием внешней силы свободный конец пружины переместился и занял положение, характеризующееся радиус-вектором r. В выбранной системе отсчета деформация пружины будет равна r. В этот момент времени, согласно условию задачи, модуль внешней силы F = kr. Тогда сама сила (как вектор) может быть представлена в виде F = kr∙i, где i – орт оси Х. Но r∙i = r, следовательно,

F = kr. Вот мы и «привязали» силу к нашей системе отсчета.

При растяжении пружины действующая на нее внешняя сила постоянно меняется по величине, следовательно, нам вновь придется применить метод исчисления бесконечно малых.

dA = F∙dr = kr∙dr.

Как Вы уже знаете, r∙dr = r∙dr, где dr – изменение модуля радиус-вектора при перемещении. Тогда dA = kr∙dr. Теперь легко найти полную работу.

а). А = = − или А = , так как r₀ = 0.

б). А = = .

При деформации пружины в ней возникает внутренняя сила, которая до определенного предела пропорциональна величине деформации (и которая, кстати, тоже совершает работу). Эта сила называется силой упругости (на рисунке не показана). Если пружина растягивается равномерно, то в любой момент времени величина силы упругости F_упр будет равна величине внешней силы F. Следовательно, выражение для упругой силы будет иметь вид F_упр = − kr.

Очевидно, что работа этой силы будет равна работе внешней силы, взятой с противоположным знаком, поскольку сила упругости имеет направление, противоположное направлению внешней силы. Итак,

а). А_упр = − или А_упр = − , так как r₀ = 0.

б). А_упр = .

Ответ: а). А = , А_упр = − ; б) А = , А_упр = .

Задача 12. Частица совершила перемещение по некоторой траектории в плоскости XY из точки 1 с радиус-вектором r₁ = i + 2j в точку 2 с радиус-вектором r₂ = 2i – 3j. При этом на нее действовали некоторые силы, одна из которых F = 3i + 4j. Найти работу А этой силы.

Дано: r₁ = i + 2j, r₂ = 2i – 3j, F = 3i + 4j.

А − ?

Решение.

Перемещение частицы Δr = r₂ − r₁ = 2i – 3j − i − 2j = i – 5j. Поскольку действующая на частицу сила F постоянна, то ее работа

А = F∙Δr = (3i + 4j)∙(i – 5j).

Выполнив умножение, получим

А = 3i² − 15ij + 4ji − 20j².

Так как скалярное произведение взаимно перпендикулярных ортов равно нулю, а i² = 1 и j² = 1, то А = − 17 Дж.

Ответ: А = − 17 Дж.

Задача 13. Тело массы m с постоянной скоростью втаскивают с поверхности Земли на наклонную плоскость с помощью постоянной силы F, направленной параллельно плоскости. Найти работу всех сил (по отдельности), действующих на тело при его поднятии на высоту h от основания. Плоскость наклонена к горизонту под углом α.

Дано: F, h, α.

R − ? А_F − ? A_mg − ? A_R − ?

Решение.

Тело взаимодействует с тремя объектами, а именно: с Землей, с наклонной плоскостью и с каким-то телом, являющимся причиной возникновения силы F. Поэтому на тело действуют три силы. Сила, действующая со стороны Земли – это сила тяжести mg, сила, действующая со стороны плоскости – это сила реакции R плоскости и еще – сила F (см. рисунок).

П оскольку тело движется с постоянной скоростью, то его ускорение равно нулю. Тогда второй закон Ньютона запишется так: mg + R + F = 0. Отсюда