§ 12.2. Импульс

Задача 1. Бильярдный шар с массой m и скоростью v₀ летит перпендикулярно гладкой неподвижной стенке и испытывает с ней абсолютно упругий удар. Найти изменение импульса шара, модуль этого изменения и изменение модуля импульса шара.

Дано: m, v₀.

Δр − ? | Δр | − ? Δр − ?

Решение.

Рассмотрим шар в двух состояниях: до удара о стенку и − после.

До удара его импульс p₀ = mv₀. После удара его импульс p₁ = mv₁, где v₁ – скорость шара после удара.

У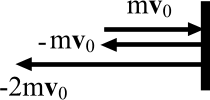 дар о гладкую неподвижную стенку является абсолютно упругим, а это значит, что, во-первых, модуль скорости шара не изменился, то есть v₀ = v₁, а, во-вторых, величина угла падения шара на стенку равна величине угла отражения (отскока). При этом угол измеряется между направлением скорости падения (или отскока) и перпендикуляром к стенке в точке соприкосновения с ней шара.

Следовательно, в данном случае шар отлетит от стенки по той же линии, что и при подлете.

Изменение или (что то же самое) приращение Δр импульса есть разность между его конечным и начальным значениями, то есть Δр = p₁ − p₀. Поскольку v₁ есть вектор, противоположный (или обратный) вектору v₀, то v₁ = − v₀, и p₁ = − mv₀. Тогда Δр = − mv₀ − mv₀, то есть Δр = − 2mv₀. Модуль этого вектора изменения импульса шара | Δр | = 2mv₀.

Модуль импульса шара до удара о стенку p₀ = mv₀. После удара модуль его импульса p₁ = mv₁. Но v₁ = v₀, следовательно, p₁ = p₀, то есть модуль импульса остался прежним. Тогда Δр = p₁ − p₀ = 0, а это значит, что изменения модуля импульса не произошло.

Ответ: Δр = − 2mv₀, | Δр | = 2mv₀, Δр = 0.

Задача 2. Бильярдный шар с массой m и скоростью v₀ летит под углом α = 30⁰ к гладкой неподвижной стенке и испытывает с ней абсолютно упругий удар. Найти модуль изменения и изменение модуля импульса шара.

Дано: m, v₀, α = 30⁰.

| Δр | − ? Δр − ?

Решение.

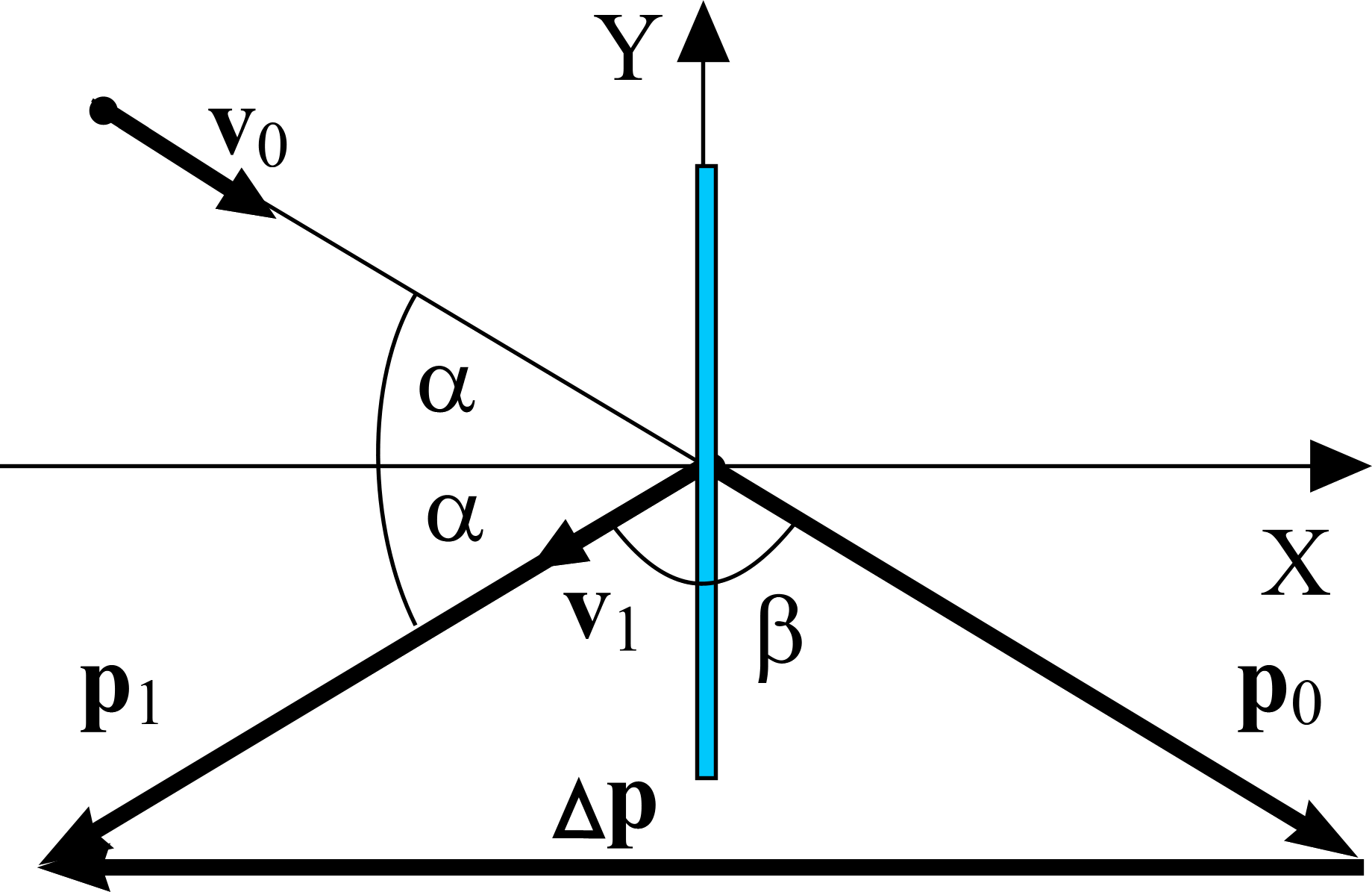
Изменение импульса Δр = p₁ − p₀ = mv₁ − mv₀, где p₀ − импульс шара до удара о стенку, p₁ – после удара. Модуль этого вектора можно найти одним из двух способов, предложенных в задаче 11.5.9. Воспользуемся вторым способом. Возведем в квадрат обе части векторного равенства Δр = mv₁ − mv₀:

(Δр)² = (mv₁ − mv₀)² = (mv₁)² – 2m²v₁v₀ + (mv₀)².

Вспоминаем, что квадрат вектора есть квадрат его модуля, а v₁v₀ = v₁v₀ Cos β. Тогда | Δр |² = m²v² – 2m²v² Cos 120⁰ + m²v².

В этом выражении учтено, что при абсолютно упругом ударе модули скоростей равны и введено обозначение: v₁ = v₀ = v. Тогда

| Δр |² = 2m²v² (1 – Cos 120⁰ ) = 3m²v², так как Cos 120⁰ = − 0,5. Извлекая квадратный корень, получим:

| Δр | ≈ 1,7 mv кг·м/с.

Вспомнив решение предыдущей задачи, можем сразу написать: Δр = 0, то есть изменения модуля вектора импульса при отскоке шарика не произошло.

Ответ: | Δр | ≈ 1,7 mv кг·м/с, Δр = 0.

Задача 3. Тело массой m = 0,5 кг бросают под углом α = 30⁰ к горизонту с высоты h = 25 м со скоростью, величина которой v₀ = 5 м/с. Найти модуль изменения и изменение модуля импульса при ударе тела о землю.

Дано: m = 0,5 кг, v₀ = 5 м/с, h = 25 м, α = 30⁰.

| Δр | − ? Δр − ?

Решение.

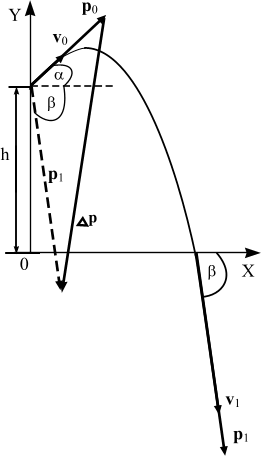
В момент t = t₁ удара о землю тело имеет скорость v₁. При этом импульс тела p₁ = mv₁. Изменение импульса Δр = p₁ – p₀, где p₀ = mv₀ – количество движения тела в момент броска. Тогда Δр = mv₁ − mv₀. (1)

Для нахождения модуля вектора изменения импульса следует рассмотреть треугольник, сторонами которого являются модули векторов p_1, p₀, Δр. По теореме косинусов найдем модуль вектора изменения импульса.

| Δр | = m 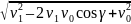. (2)

Для тех, кто забыл теорему косинусов, напомню, что ее легко получить с помощью положений векторной алгебры, как это показано в задаче № 9 (см. «Векторная алгебра» меню сайта). Думаю, нелишне вспомнить получение этой теоремы на примере данной задачи.

Возведем в квадрат обе части равенства (1):

(Δр)² = (mv₁ − mv₀)² = (mv₁)² – 2m²v₁v₀ + (mv₀)² = m² – 2m² v₁v₀ Cos γ + m² .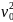

Тогда | Δр | = m .

Итак, для нахождения модуля изменения импульса тела, необходимо знать величину его скорости v₁ при ударе о землю и угол γ между направлениями конечного и начального импульсов. Все это несложно найти, если вспомнить кинематику.

Модуль скорости v₁ = 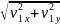, (3)

где v_1x и v_1y – проекции скорости v₁ на оси X и Y соответственно. Эти проекции найдем по формулам кинематики: v_1x = v₀ Cos α, v_1y = v₀ Sin α – gt₁ (c учетом показанных на рисунке направлений осей). Время t₁ определим из кинематического уравнения движения. При этом учтем, что в момент падения тела на землю, его ордината равна нулю. Тогда 0 = h + v₀ (Sin α) t₁ − . Подставив числа и приведя уравнение к каноническому виду, получим:

5 – 2,5 t₁ – 25 = 0. Решив это квадратное уравнение, будем иметь t₁ = 2,5 c. Найдем проекции скорости v₁ на координатные оси:

v_1x = 5 Cos 30⁰, v_1y = 5 Sin 30⁰ – 2,5 g или v_1x = 4,3 м/с, v_1y = – 22,5 м/с. Подставив эти значения в (3), найдем v₁ = 23 м/с.

Теперь найдем величину угла β между v₁ и горизонтом. Поскольку v_1x = v₁ Cos β, то Cos β = . Подставив числа, получим Cos β = 0,19, откуда β = 79⁰.

Так как γ = α + β, то γ = 109⁰. Учитывая, что Cos 109⁰ = − 0,326, из формулы (2) найдем | Δр | = 12,3 кгм/с.

Величина начального импульса тела p₀ = mv₀ = 0,5∙5 кгм/с = 2,5 кгм/с, а величина конечного импульса p₁ = mv₁ = 0,5∙23 кгм/с = 11,5 кгм/с.

Тогда Δр = p₁ – p₀ = 9 кгм/с.

Следует заметить, что предложенный способ нахождения | Δр | необходимо использовать, если по условию задачи нельзя найти силу, вызывающую изменение импульса тела. В том случае (как в этой задаче), когда такую силу можно найти, удобнее воспользоваться законом изменения импульса тела. В нашем случае этой силой является сила тяжести mg. Тогда mg t₁ = | Δр |. Подставив числа, придем практически к полученному ранее результату,

Ответ: | Δр | = 12,3 кгм/с, Δр = 9 кгм/с.

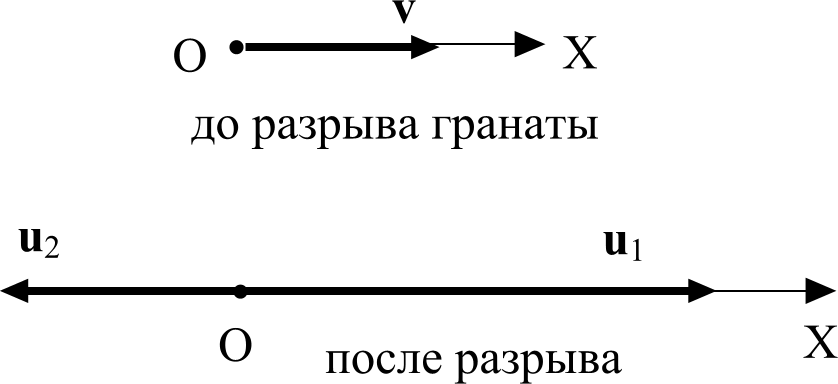
Задача 4. Граната, летящая со скоростью, равной по величине v = 10 м/с, разорвалась на два осколка. Больший осколок, масса которого m₂ составляла 0,6 массы m всей гранаты, продолжал двигаться в прежнем направлении, но с большей по модулю скоростью u₁ = 25 м/с. Найти величину скорости u₂ меньшего осколка.

Дано v = 10 м/с, m₂ = 0,6 m, u₁ = 25 м/с.

u₂ − ?

Решение.

До того, как граната разорвалась, ее импульс р₀ = mv. После взрыва гранаты ее импульс р₁ = m₁u₁ + m₂u₂, где m₁ – масса меньшего осколка. Очевидно, m₁ = 0,4m. Тогда

р₁ = 0,4 mu₁ + 0,6 mu₂.

Силы, возникающие при взрыве гранаты, настолько велики, что систему граната – два ее осколка можно считать замкнутой. Следовательно, полный вектор импульса системы за время взрыва не меняется: р₀ = р₁, или v = 0,6 u₁ + 0,4 u₂. Проектируем это векторное равенство на ось Х, совпадающую с направлением движение гранаты:

v_х = 0,6 u_1х + 0,4 u_2х. Поскольку v_х = v, u_1х = u₁, то

u_2х = 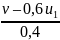. Подставив числа, получим u_2х = − 12,5 м/с.

Проектирование на ось Y, перпендикулярную оси Х, даст уравнение

0 = 0 + 0,4 u_2y, откуда следует, u_2y = 0. Таким образом, составляющая скорости по оси Y меньшего осколка отсутствует. Следовательно, он будет двигаться вдоль оси Х в сторону, противоположную направлению v и u₂. Модуль скорости меньшего осколка u₂ = 12,5 м/с.

Ответ: u₂ = 12,5 м/с.

Задача 5. На рельсах стоит платформа массой m₁ = 10 т. На платформе закреплено орудие массой m₂ = 5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m₃ = 100 кг; величина его скорости при вылете из ствола относительно орудия v₀ = 500 м/с. Найти величину и направление скорости u платформы в первый момент после выстрела, если: а) платформа двигалась со скоростью, величина которой v = 5 м/с, и выстрел был произведен в направлении ее движения; б) платформа двигалась со скоростью, величина которой v = 5 м/с, и выстрел был произведен в направлении, противоположном направлению ее движения; в) платформа стояла неподвижно.

Дано m₁ = 10 т = 10⁴ кг, m₂ = 5 т = 5∙10³ кг, m₃ = 100 кг, v₀ = 500 м/с, v = 5 м/с.

u − ?

Решение.

Рассмотрим систему, состоящую из платформы, орудия и снаряда в двух состояниях: до выстрела и после выстрела. До выстрела импульс системы

р₀ = (m₁ + m₂ + m₃) v.

После выстрела р₁ = (m₁ + m₂) u + m₃v₁, где v₁ – скорость снаряда относительно земли. Надо помнить, что в формулу, по которой рассчитывается импульс системы, должны входить скорости, вычисленные относительно какой-то одной системы отсчета. Если данную задачу решать в системе отсчета, связанной с землей, то и скорость снаряда должна быть определена относительно земли. Учитывая, что v₁ – абсолютная скорость снаряда, v₀ – его относительная скорость, v – переносная скорость, запишем закон сложения скоростей: v₁ = v₀ + v. Тогда

р₁ = (m₁ + m₂) u + m₃ (v₀ + v).

Запишем закон сохранения количества движения системы в проекциях на ось X, направление которой пусть совпадает с первоначальным направлением движения платформы. Тогда р_0х = р_1х или

(m₁ + m₂ + m₃) v_х = (m₁ + m₂) u_х + m₃ (v_0х + v_х).

а) выстрел произведен в направлении движения платформы. Тогда v_х = v, v_0х = v₀, следовательно, (m₁ + m₂ + m₃) v = = (m₁ + m₂) u_х + m₃ (v₀ + v). Отсюда находим

u_х = .

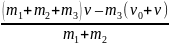Подставив числа, получим u_х = 1,7 м/с, то есть платформа движется в первоначальном направлении со скоростью, модуль которой u = 1,7 м/с.

б) выстрел произведен в направлении, противоположном направлению движения платформы. В этом случае v_х = v, v_0х = − v₀. Тогда

(m₁ + m₂ + m₃) v = (m₁ + m₂) u_х + m₃ (− v₀ + v). Отсюда находим

u_х = .

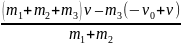Подставив числа, получим u_х = 8,3 м/с, то есть платформа движется в первоначальном направлении со скоростью, модуль которой u = 8,3 м/с.

в) выстрел произведен с неподвижной платформы. Будем считать, что выстрел произведен в направлении оси Х. В этом случае v_х = 0 (следовательно, и v = 0),

v_0х = v₀. Тогда 0 = (m₁ + m₂) u_х + m₃ v₀ . Отсюда находим u_х = .

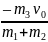Подставив числа, получим u_х = − 3,3 м/с, то есть платформа движется в направлении, противоположном направлению оси Х, со скоростью, модуль которой u = 3,3 м/с.

Ответ: а) u = 1,7 м/с, платформа движется в первоначальном направлении;

б) u = 8,3 м/с, платформа движется в первоначальном направлении;

в) u = 3,3 м/с, платформа движется в направлении, противоположном направлению оси Х.

Задача 6. Человек массой m₁ = 60 кг, бегущий со скоростью, величина которой v₁ = 9 км/ч, вскакивает на тележку массой m₂ = 70 кг, движущуюся со скоростью, равной по величине v₂ = 1,8 км/ч. С какой скоростью u будет двигаться тележка, если: а) человек догонял тележку; б) человек бежал ей навстречу?

Дано: m₁ = 60 кг, v₁ = 9 км/ч = 2,5 м/с, m₂ = 70 кг,

v₂ = 1,8 км/ч = 0,5 м/с.

u − ?

Решение.

Рассмотрим систему, состоящую из человека и тележки в двух состояниях: до того, как человек вскочил на тележку и после этого. Вначале импульс системы

р₀ = m₁v₁ + m₂v₂. После того, как человек оказался на тележке р₁ = (m₁ + m₂) u.

Запишем закон сохранения количества движения системы в проекциях на ось X, направление которой пусть совпадает с первоначальным направлением движения тележки. Тогда р_0х = р_1х или m₁v_1х + m₂v_2х = (m₁ + m₂) u_х.

Отсюда u_х = .

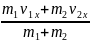а) человек догоняет тележку. Тогда v_1х = v₁, v_2х = v₂, следовательно,

u_х = 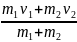. Подставив числа, получим u_х = 1,4 м/с. Тележка движется в первоначальном направлении со скоростью, модуль которой u = 1,4 м/с.

б) человек бежит навстречу тележке. Тогда v_1х = − v₁, v_2х = v₂, следовательно,

u_х = 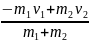. Подставив числа, получим u_х = − 0,9 м/с. Тележка движется в направлении, противоположном начальному, со скоростью, модуль которой

u = 0,9 м/с.

Ответ: а) u = 1,4 м/с, тележка движется в первоначальном направлении;

б) u = 0,9 м/с, тележка движется в направлении, противоположном начальному.

Задача 7. На рельсах, на горизонтальной плоскости стоит платформа с песком общей массой m₁ = 5∙10³ кг. В платформу попадает снаряд массой m₂ = 5 кг и застревает в песке. Найти величину u скорости платформы, если снаряд летел вдоль рельсов со скоростью, величина которой v = 400 м/с под углом α = 60⁰ к горизонту.

Дано: m₁ = 5∙10³ кг, m₂ = 5 кг, v = 400 м/с, α = 60⁰.

u − ?

Решение.

Непосредственно с помощью законов Ньютона эту задачу не решить. Дело в том, что платформа приобретает скорость в результате взаимодействия со снарядом, а сила этого взаимодействия сложным образом зависит от времени, и закон изменения этой силы нам не известен.

Решить задачу с помощью закона сохранения импульса тоже не представляется возможным без дополнительных ограничений на характер взаимодействия платформы с песком и снаряда.

Действительно, кроме внутренней силы взаимодействия снаряда с платформой на систему снаряд – платформа действуют две внешние силы: сила тяжести и сила реакции со стороны рельсов. И, если сила тяжести во время взаимодействия не изменяется, то о силе реакции этого сказать нельзя. В то же время мы знаем, что эта сила представляет собой векторную сумму силы трения и силы нормальной реакции. Если пренебречь силой трения, то оставшиеся внешние силы (сила тяжести и сила нормальной реакции) будут перпендикулярны горизонтальному направлению. Конечно, сила нормальной реакции в процессе взаимодействия снаряда с платформой будет изменяться, но ее проекция на горизонтальное направление (как и проекция силы тяжести) будет равна нулю. Тогда мы можем применить закон сохранения проекции полного импульса системы на горизонтальное направление. Можно ли пренебречь силой трения? Пренебречь можно чем угодно, другое дело, насколько это корректно с точки зрения приемлемой точности конечного результата. В данном случае пренебрежение силой трения вполне допустимо, поскольку она заведомо меньше силы взаимодействия снаряда и платформы.

После таких допущений, запишем закон сохранения системы снаряд – платформа в проекциях на горизонтальную ось Х: p_0x = p_1x, где p_0x – проекция общего импульса системы до взаимодействия, p_1x − то же после взаимодействия.

Поскольку платформа до взаимодействия покоилась, то

p_0x = m₂v_x = m₂v Cos α.

После взаимодействия

p_1x = (m₁ + m₂) u_x.

Пусть направление оси совпадает с направлением u, тогда

m₂v Cos α = (m₁ + m₂) u, откуда

u = .

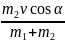Подставив числа, получим u = 0,2 м/с.

Ответ: u = 0,2 м/с.

Задача 8. Два человека на роликовых коньках стоят друг против друга. Масса первого человека m₁ = 70 кг, а второго m₂ = 80 кг. Первый бросает второму груз массой m = 10 кг со скоростью, величина горизонтальной составляющей которой v = 5 м/с относительно земли. Определить модуль v₁ скорости первого человека после бросания груза и модуль v₂ скорости второго после того, как он поймает груз. Трением пренебречь.

Дано: m₁ = 70кг, m₂ = 80 кг, m = 10 кг v = 5 м/с.

v₁ − ? v₂ − ?

Решение.

Вначале рассмотрим систему, состоящую из человека массой m₁ и груза. В исходном состоянии импульс системы равен нулю, поскольку и человек и груз неподвижны. После того, как груз был брошен, количество движения системы, в общем, изменилось, однако, изменения импульса системы по горизонтали не произошло. Это связано с тем, что сумма проекций всех внешних сил на горизонтальное направление равна нулю, поскольку сила тяжести и сила нормальной реакции горизонтальной поверхности перпендикулярны горизонтальному направлению, а силой трения пренебрегаем.

Проекция полного импульса системы на указанное направление

p_1x = m₁v_1x + mv_x = 0. Если ось Х направить от первого человека (с массой m₁) ко второму, то v_x = v. Тогда v_1x = 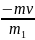. С учетом числовых значений v_1x = − 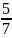м/с, то есть человек, бросивший груз, будет удаляться от другого человека со скоростью, величина которой v₁ = м/с.

Теперь рассмотрим систему, состоящую из человека массой m₂ и груза. До того, как был пойман груз, проекция полного импульса системы на ось Х p_2x = mv (направление оси оставлено прежним). После того, как человек поймал груз, проекция импульса стала (m + m₂) v_2x. Следовательно, mv = (m + m₂) v_2x, откуда v_2x = 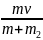. Подставив числа, получим v_2x = 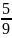м/с, то есть человек, поймавший груз, начнет удаляться от первого человека со скоростью, величина которой

v₂ = м/с.

Ответ: v₁ = м/с, v₂ = м/с.

Задача 9. По горизонтальным рельсам со скоростью величиной v = 19,8 км/ч движется платформа массой m₁ = 200 кг. На нее вертикально падает камень массой m₂ = 50 кг и движется в дальнейшем вместе с платформой. Через некоторое время в платформе открывается люк, и камень проваливается вниз. С какой по величине скоростью u′ движется после этого платформа? Трением между платформой и рельсами пренебречь.

Дано: v = 19,8 км/ч = 5,5 м/с, m₁ = 200 кг, m₂ = 50 кг.

u′ − ?

Решение.

Рассмотрим систему, состоящую из платформы и камня в трех состояниях:

1) камень еще не упал на платформу; 2) камень находится на платформе и движется вместе с ней; 3) камень находится вне платформы (провалился вниз).

В первом состоянии проекция полного импульса системы на горизонтальное направление p_0x = m₁v_x, поскольку камень падает на платформу вертикально, и проекция его импульса на горизонтальное направление равна нулю.

Во втором состоянии проекция полного импульса системы на горизонтальное направление p_1x = (m₁ + m₂) u_x, где u_x – проекция скорости u системы на указанное направление. Так как силы, действующие на систему в горизонтальном направлении, отсутствуют, то p_0x = p_1x или m₁v_x = (m₁ + m₂) u_x. Если выбрать ось Х так, что ее направление совпадает с направлением движения платформы, то

v_x = v. Тогда u_x = 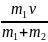. Подставив числа, получим u_x = 4,4 м/с, то есть вагон продолжает двигаться в прежнем направлении со скоростью, модуль которой

u = 4,4 м/с.

В третьем состоянии проекция полного импульса системы на горизонтальное направление p_2x = m₁ 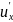+ m₂ u_x. Здесь, m₁ − проекция импульса платформы на ось Х ( − проекция скорости u′ платформы, которую она стала иметь после того, как выпал камень), m₂ u_x – проекция импульса камня на ось Х, после того, как он провалился в люк (проекция скорости камня не изменилась, так как при падении с платформы на него не действовали никакие горизонтальные силы).

Поскольку при выпадении камня на систему не действовали силы в горизонтальном направлении, то p_1x = p_2x или (m₁ + m₂) u_x = m₁ + m₂ u_x. Отсюда следует, что = u_x или u′ = u, то есть величина скорости платформы, после того, как с нее выпал камень, не изменилась. Таким образом, u′ = 4,4 м/с.

Ответ: u′ = 4,4 м/с.

Задача 10. Две лодки движутся по инерции параллельными курсами навстречу друг другу. Когда лодки поравнялись, с одной из них на другую осторожно перебросили груз массой m = 5 кг. После этого лодка, на которую перебросили груз, остановилась, а другая продолжала движение со скоростью, равной по величине u₂ = 8 м/с. С какими по величине скоростями v₁ и v₂ двигались лодки до встречи, если масса лодки, в которую перебросили груз, m₁ = 200 кг?

Дано: m = 5 кг, u₁ = 0 м/с, u₂ = 8 м/с, m₁ = 200 кг.

v₁ − ? v₂ − ?

Решение.

Выберем две системы: 1) первая лодка (с массой m₁) – груз; 2) вторая лодка – груз. Каждую систему рассмотрим в двух ее состояниях.

Начнем с первой системы. Ее начальное состояние: лодка движется со скоростью v₁, груз движется в противоположном направлении со скоростью v₂ (он находится во второй лодке). Полный импульс системы в этом состоянии m₁v₁ + mv₂. Конечное состояние: груз лежит в первой лодке. Полный импульс системы по условию задачи равен нулю. При переходе из начального состояния в конечное проекции на горизонтальное направление всех сил, действующих на систему, равны нулю, следовательно, проекция на это направление полного импульса системы сохраняется, то есть m₁v_1х + mv_2х = 0. Пусть горизонтальная ось Х направлена в сторону движения первой лодки, тогда v_1х = v₁, v_2х = − v₂. Следовательно, m₁v₁ − mv₂ = 0, откуда

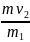v₁ = . (1)

Теперь рассмотрим вторую систему. Ее начальное состояние: лодка с грузом движется со скоростью v₂. Проекция на ту же ось Х полного импульса системы в этом состоянии m₂v_2х + mv_2х, где m₂ – масса второй лодки. Конечное состояние: груз уже не находится во второй лодке (но еще и не лежит в первой!). Проекция полного импульса системы в этом состоянии m₂u_2х + mv_2х. Здесь учтено, что скорость груза в направлении движения лодки не изменилась.

При переходе из начального состояния в конечное проекции на горизонтальное направление всех сил, действующих на систему, равны нулю, следовательно, проекция на это направление полного импульса системы сохраняется, то есть m₂v_2х + mv_2х = m₂u_2х + mv_2х. Но отсюда следует, что u_2х = v_2х, а, значит, v₂ = u₂.

Итак, v₂ = 8 м/с. Подставив числа в (1), получим v₁ = 0,2 м/с.

Ответ: v₁ = 0,2 м/с, v₂ = 8 м/с.

Задача 11. Три лодки одинаковой массы М движутся друг за другом с одинаковой по величине скоростью v. Из средней лодки в крайние одновременно перебрасывают грузы массой m каждый со скоростью величиной u относительно лодок. Какие по величине скорости будут иметь лодки после перебрасывания грузов? Сопротивлением воды и воздуха пренебречь.

Дано: М, v, m, u.

v₁ − ? v₂ − ? v₃ − ?

Решение.

Выберем три системы: 1) первая лодка – груз; 2) вторая (средняя) лодка – грузы (оба); 3) третья лодка – груз. Каждую систему рассмотрим в двух ее состояниях.

Начнем с первой системы. Ее начальное состояние: лодка движется со скоростью v, груз движется в том же направлении со скоростью u₁ относительно лодки (он уже покинул вторую лодку). Для нахождения полного импульса системы следует иметь в виду, что скорость лодки дана относительно земли (неподвижной системы отсчета), то есть v – это абсолютная скорость лодки.

Скорость же груза представлена в движущейся системе отсчета, связанной с лодкой. Для нахождения полного импульса системы следует «привязать» все скорости к какой-то одной системе отсчета. Выберем для этого систему отсчета, связанную с землей и найдем скорость груза в этой системе отсчета. Поскольку v – это переносная скорость груза, то его скорость в неподвижной системе отсчета будет u₁ + v. Тогда полный импульс системы в ее начальном состоянии определится формулой Мv + m (u₁ + v). Конечное состояние системы: груз лежит в первой лодке. Полный импульс системы в этом состоянии (М + m) v₁. При переходе из начального состояния в конечное проекции на горизонтальное направление всех сил, действующих на систему, равны нулю, следовательно, проекция на это направление полного импульса системы сохраняется, то есть

Мv_х + m (u_1х + v_x) = (М + m) v_1х. Пусть горизонтальная ось Х направлена в сторону движения лодки, тогда v_х = v, u_1х = u₁ = = u.

Следовательно, Мv + m (u + v) = (М + m) v_1х, откуда

v_1х = 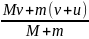. Модуль этой скорости v₁ = .

Теперь рассмотрим вторую систему. Ее начальное состояние: лодка движется со скоростью v, грузы общей массой 2m находятся в лодке и, естественно, движутся в том же направлении и с той же скоростью, что и лодка. Полный импульс системы в этом состоянии (М + 2m) v.

Конечное состояние: грузы летят каждый в свою сторону, лодка продолжает свое движение со скоростью v₂ уже без грузов. Полный импульс системы в этом состоянии Мv₂ + m (u₁ + v) + m (u₂ + v), где u₂ – относительная скорость груза, летящего к третьей лодке (то есть, противоположно направлению оси Х). При переходе из начального состояния в конечное проекции на горизонтальное направление всех сил, действующих на систему, равны нулю, следовательно, проекция на это направление полного импульса системы сохраняется, то есть

(М + 2m) v_х = Мv₂ + m (u_1х + v_х) + m (u_2х + v_х).

После нахождения проекций (учитывая, что u_2х = − u₂ = − u) и выполнения несложных преобразований, получим v₂ = v, то есть величина скорости второй лодки не изменилась.

Наконец, третья система. Здесь ситуация аналогична той, которая рассматривалась для первой лодки, только вместо u₁ будет фигурировать u₂. Проведя подобные рассуждения, получим v₃ = .

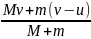Ответ: v₁ = , v₂ = v, v₃ = .

Задача 12. Лодка стоит неподвижно в стоячей воде. Человек, находящийся в лодке, переходит с кормы на нос, двигаясь с постоянной скоростью. На какое расстояние h сдвинется лодка, если масса человека m = 60 кг, масса лодки М = 120 кг, длина лодки L = 3 м? Сопротивлением воды пренебречь.

Дано: m = 60 кг, М = 120 кг, L = 3 м.

h − ?

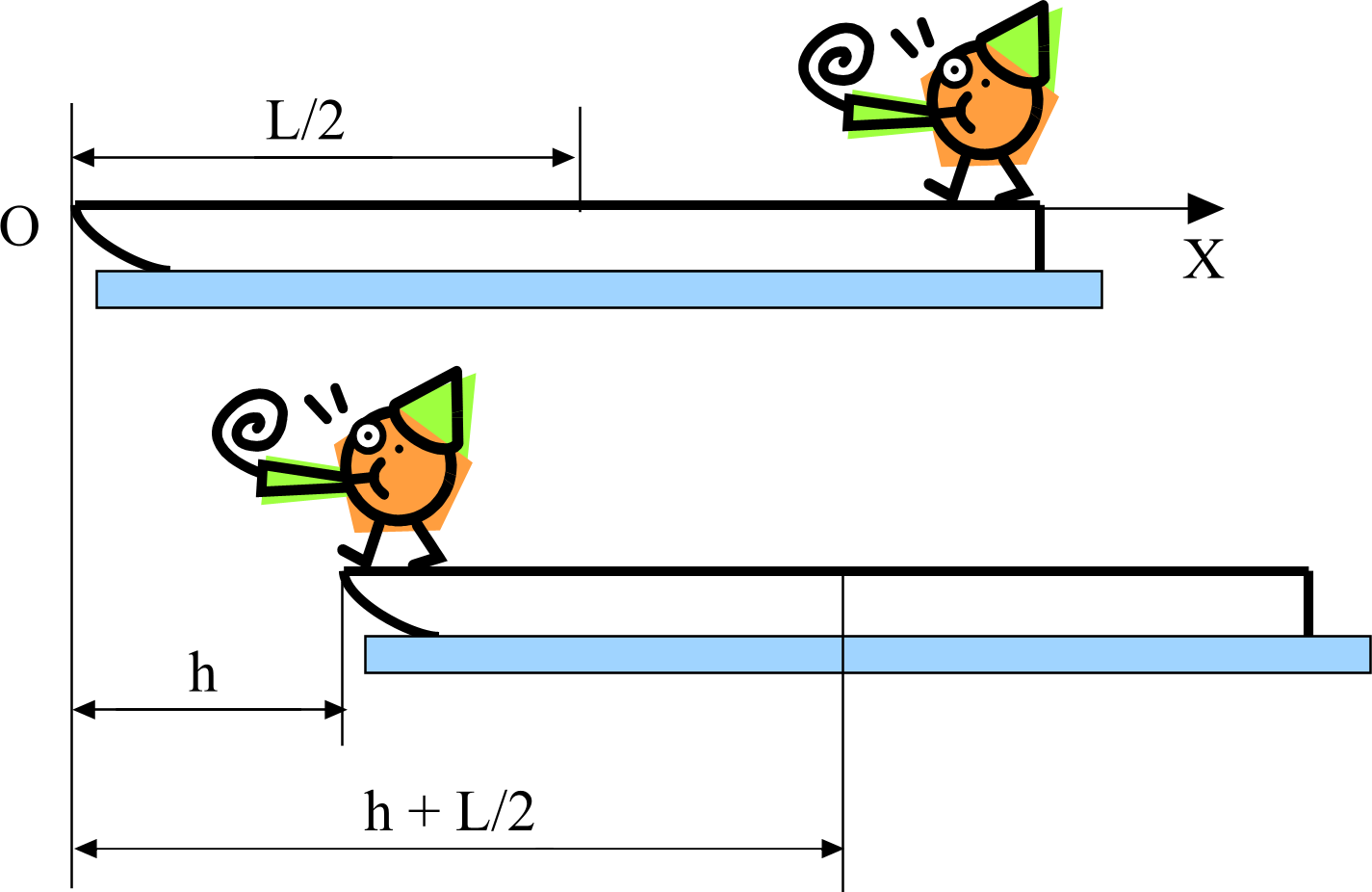
Решение.

Обычно эту (и подобные ей) задачу решают одним из двух способов. Рассмотрим их.

Первый способ.

Рассмотрим систему человек – лодка в двух состояниях. В начальном состоянии человек покоится на корме. Покоится и лодка. Полный импульс системы равен нулю. Затем человек пошел к носу лодки. Пусть его скорость относительно лодки v. Поскольку человек приобрел импульс, направленный от кормы к носу, то лодка «обязана» начать двигаться в противоположном направлении и с такой скоростью u (относительно берега), чтобы полный импульс системы по горизонтали всегда оставался равным нулю (ведь по горизонтали на систему не действуют никакие силы). Проследим за человеком вплоть до того момента, когда он пришел на нос лодки, имея в этот момент все ту же скорость v. Это мгновение мы и выберем при рассмотрении конечного состояния системы. В этот момент времени система имеет импульс mv′ + Mu, где v′ − скорость человека относительно берега (не забывайте, что скорости всех частей системы должны быть «привязаны» к одной и той же системе отсчета). Поскольку v – относительная скорость человека, u – его переносная скорость, то v′ = v + u. Тогда импульс системы в конечном состоянии равен m (v + u) + Mu. И этот импульс, спроектированный на горизонтальное направление, как уже было сказано, должен быть равен нулю, то есть, m (v_х + u_х) + Mu_х = 0. Выберем направление горизонтальной оси Х в сторону движения лодки. Тогда v_х = − v, u_х = u. Следовательно, m (− v + u) + Mu = 0.

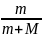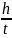Отсюда легко найти, что = . Но u = , v = 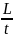, где t – время перехода системы из начального в конечное состояния. Тогда 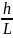= , откуда h = 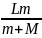. Подставив числа, получим h = 1 м.

Теперь рассмотрим второй способ решения.

Найдем координату центра масс системы человек – лодка в двух состояниях: начальном и конечном.

В начальном состоянии указанная координата х_н = .

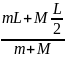В конечном состоянии х_к = .

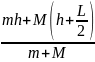Поскольку начальная скорость центра масс равна нулю (лодка и человек вначале покоились), и никакие силы в горизонтальном направлении на систему не действовали, то координата центра масс системы в горизонтальном направлении не изменится. Тогда, приравнивая х_н = х_к, после несложных преобразований получим h = .

Ответ: h = 1 м.

Задача 13. Лягушка массы m сидит на конце доски массы М и длины L. Доска покоится на поверхности пруда. Лягушка прыгает под углом α к горизонту вдоль доски. Какой должна быть при этом величина v₀ скорости лягушки, чтобы после прыжка лягушка оказалась на другом конце доски? Сопротивлением воды пренебречь.

Дано: m, М, L, α.

v₀ − ?

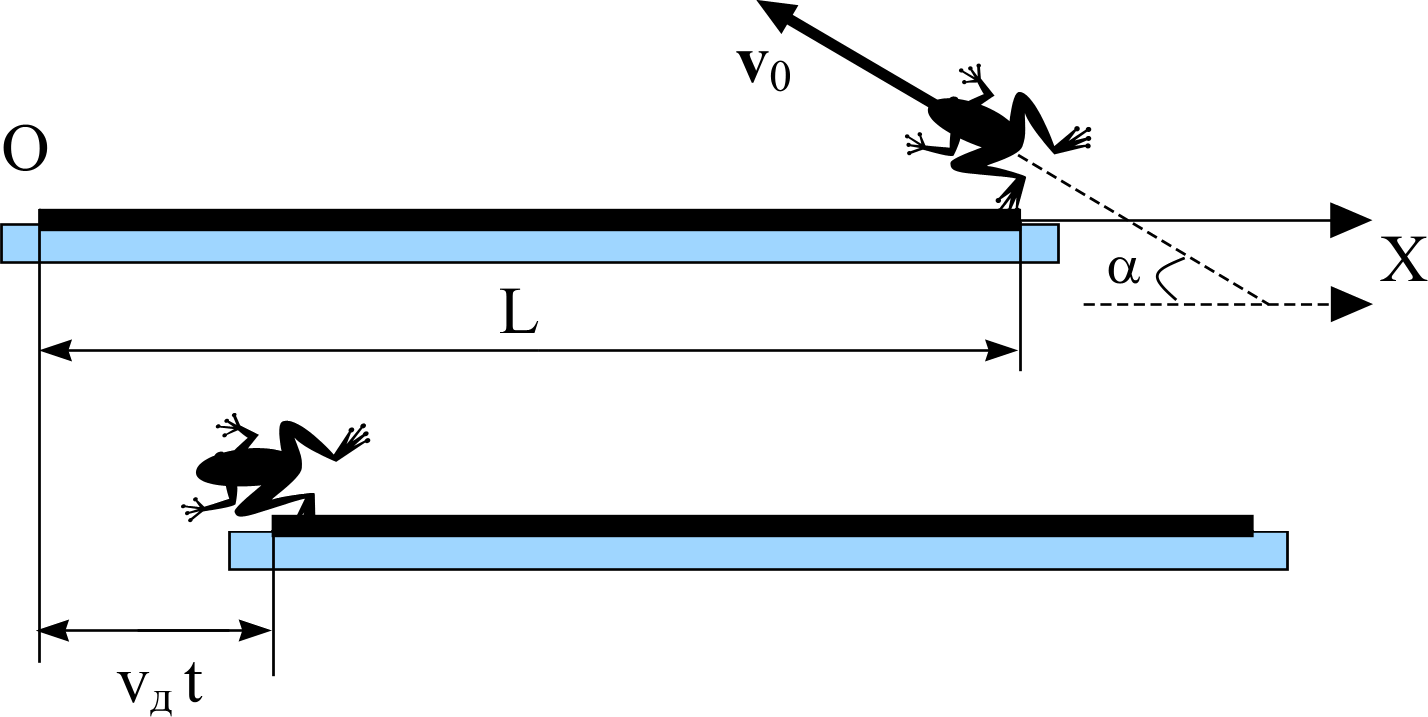
Решение.

Рассмотрим систему доска – лягушка в двух состояниях: до отрыва лягушки от доски и в момент, после которого она уже находится на другом конце доски. В первый момент полный импульс системы равен нулю, поскольку и доска и лягушка покоились. Во второй момент времени полный импульс системы равен Mu + mv, где u – скорость доски, v – скорость лягушки (скорости будем рассматривать по отношению к неподвижной системе отсчета, связанной с землей). Поскольку в горизонтальном направлении на систему не действуют никакие силы, то проекция на горизонтальное направление полного импульса системы сохраняется, то есть Mu_х + mv_х = 0. Пусть горизонтальная ось Х направлена в сторону движения доски.

Тогда u_х = u, v_х = − v₀ Cos α (здесь надо вспомнить кинематику: горизонтальная составляющая скорости не меняется. Будет полезно, если Вы вновь прочитаете решение задачи 11.2.13).

Тогда Mu − mv₀ Cos α = 0, откуда u = .

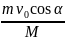Движение лягушки происходит в поле силы тяжести Земли, то есть она движется с постоянным ускорением g.

Во время полета горизонтальная координата лягушки меняется по закону

х_л = L – v₀ (Cos α) t, а координата тех точек доски, куда «приземлится» лягушка – по закону х_д = ut, или, учитывая найденное выше выражение для u,

х_д = t. В момент t = t₁, когда лягушка «приземлится» указанные координаты будут одни и те же, то есть L – v₀ (Cos α) t₁ = 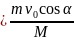t₁. Время, в течение которого лягушка находилась в воздухе, t₁ = (в задаче 11.2.13, где приведен вывод этой формулы, данное время обозначено как t₂).

Если подставить это выражение в предыдущее уравнение и выполнить несложные преобразования, то можно найти v₀:

v₀ = .

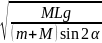Ответ: v₀ = .

Задача 14. Легкий шарик массой m, движущийся со скоростью v₀, налетает на массивную плиту, перпендикулярно ее поверхности. Плита движется со скоростью u в противоположном направлении. Считая столкновение абсолютно упругим и время столкновения равным τ, определить величину v скорости шарика после столкновения и величину средней силы F_ср взаимодействия его с плитой. Масса плиты много больше массы шарика.

Дано: m, v₀, τ.

v − ? F_ср − ?

Р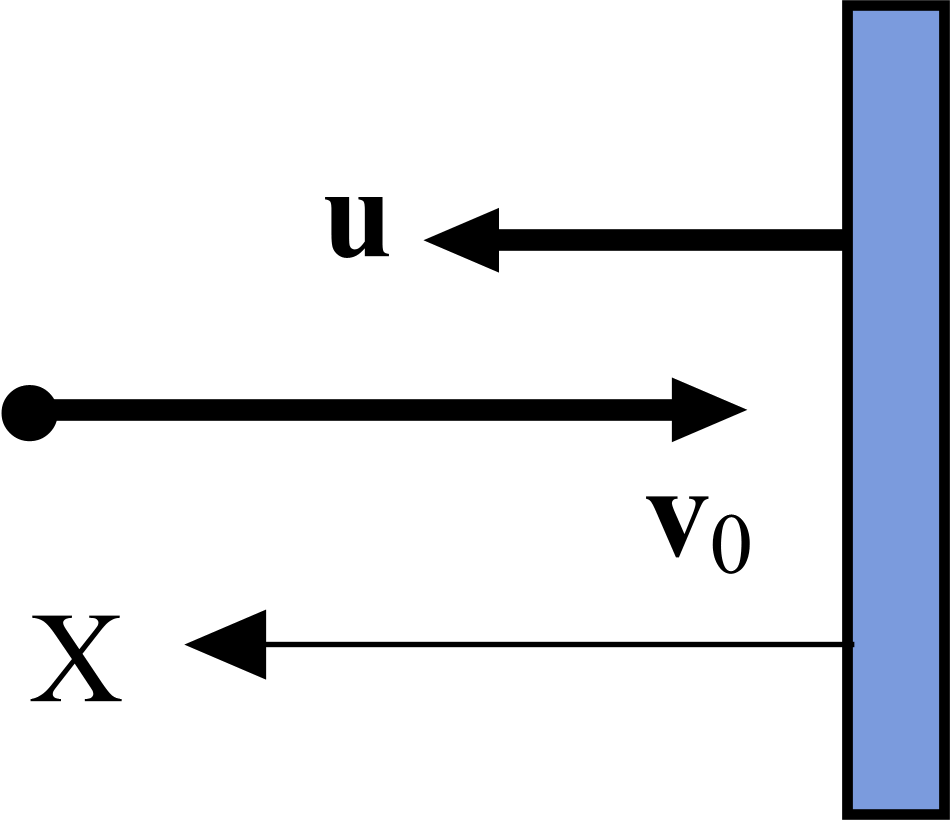 ешение.

При абсолютно упругом соударении шарик отскакивает от плиты в прямо противоположном направлении с такой же по величине скоростью относительно плиты, что и при подлете. В условии же задачи v₀ – это скорость шарика в неподвижной системе отсчета, связанной с землей. Чтобы найти скорость v_отн шарика, которую он имел, подлетая к плите, относительно самой плиты, надо учесть, что скорость u плиты это – переносная скорость. Тогда v_отн = v₀ – u. С такой же по величине, но направленной прямо противоположно скоростью v′ шарик отскочит от плиты, то есть v′ = − v_отн = u − v₀. Но это – в системе отсчета, связанной с движущейся плитой. Для нахождения скорости v отскока в неподвижной системе отсчета (абсолютную скорость), надо сложить относительную скорость отскока v′ и переносную скорость u, то есть

v = v′ + u = 2u − v₀.

Для нахождения модуля этой скорости, вначале найдем ее проекцию на ось Х, перпендикулярную плите и направленную в сторону ее движения: v_х = 2u_х − v_0х. Поскольку u_х = u, v_0х = − v₀, то v_х = 2u + v₀. Модуль же этой скорости v = 2u + v₀.

Для нахождения средней силы взаимодействия шарика и плиты, воспользуемся законом об изменении количества движения шарика. Импульс шарика до удара о плиту р₀ = mv₀. Импульс шарика после удара р = mv = m (2u − v₀). Изменение импульса Δр = р − р₀ = m (2u − v₀) − mv₀, Δр = 2m (u − v₀). Это изменение импульса шарика равно импульсу средней силы взаимодействия, то есть

2m (u − v₀) = F_ср τ. Для нахождения модуля F_ср, спроектируем последнее равенство на ту же ось Х. В результате получим F_{ср х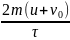} = . Таким образом, на шарик будет действовать сила, направленная вдоль оси Х (от стены), и средняя величина этой силы F_ср = .

Ответ: v = 2u + v₀, F_ср = .

Задача 15. Движение материальной точки описывается уравнением х = 25 − 10t + 2t². Приняв ее массу равной m = 3 кг, найти величину импульса в момент начала наблюдения и через t₁ = 8 с после этого. Найти величину средней силы, вызвавшей изменение импульса за указанный промежуток времени.

Дано: х = 25 − 10t + 2t², m = 3 кг, t₁ = 8 с.

p₀ − ? p₁ − ? F_ср − ?

Решение.

Дифференцирование по времени данного в условии задачи уравнения движения даст нам выражение для проекции на ось Х скорости материальной точки. Найдем это выражение.

v_x = = − 10 + 4t.

В момент начала наблюдения за движением тела, то есть, когда t = t₀ = 0, проекция скорости v_0x = − 10 м/с, и проекция импульса точки

p_0x = m v_0x = − 30 кг∙м/с.

Модуль импульса точки в это время p₀ = 30 кг∙м/с. В момент t₁ = 8 с проекция скорости v_1x = 22 м/с, и проекция импульса точки p_1x = m v_1x = 66 кг∙м/с. Этой же величине равен и сам модуль импульса, то есть p₁ = 66 кг∙м/с.

За промежуток времени Δt = t₁ − t₀ проекция импульса изменилась на

Δp_x = p_1x − p_0x, Δp_x = 96 кг∙м/с.

В соответствии с законом об изменении количества движения Δp_x = F_{ср х}∙Δt, где F_{ср х} – проекция на ось Х средней силы, действующей на точку в течение промежутка времени Δt. Тогда F_{ср х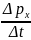} = . F_{ср х} = 12 Н.

Модуль средней силы F_ср = 12 Н.

Ответ: p₀ = 30 кг∙м/с, p₁ = 66 кг∙м/с, F_ср = 12 Н.