
- •Глава 12. Задачи на динамику
- •§ 12.1. Поступательное движение
- •§ 12.2. Импульс
- •§ 12.3. Работа
- •§ 12.4. Энергия, работа, импульс
- •§ 12.5. Вращательное движение
- •§ 12.6. Гравитация
- •§ 12.7. Колебательное движение
- •Глава 13. Твердое тело
- •§ 13.1. Кинематика твердого тела
- •§ 13.2. Динамика твердого тела
- •§ 13.3. Статика твердого тела
Равномерное и прямолинейное движение
Задача 1. Тело движется равномерно и прямолинейно от пункта А к пункту В со скоростью, величина которой v = 72 км/ч. Найти расстояния L1 и L2, на которых будет находиться тело относительно пункта В через t1 = 0,5 ч и t2 = 1,5 ч соответственно, считая, что в пункте А оно находилось в момент t = t0 = 0. Расстояние между пунктами L = 40 км. Найти пути S1 и S2, которые были пройдены за t1 и t2 соответственно.
Дано: v = 72 км/ч; t1 = 0,5 ч; t2 = 1,5 ч; L = 40 км.

L1 − ? L2 − ? S1 − ? S2 − ?
Решение.
![]()
Рис. a
Записываем кинематические уравнения движения тела:
r = r0 + vt,
Выбираем направление и начало оси Х. Пусть это будет так, как показано на рисунке (рисунок а), то есть ось направлена в сторону движения тела, а ее начало совпадает с пунктом А. Время отсчитываем от момента прохождения телом пункта А.
Проектируем векторное уравнение движения на выбранную ось:
x = x0 + vxt,
Находим проекции: x0 = 0, vx = v Cos 00 = v.
Тогда x = vt.
В момент t = t1 последнее уравнение будет выглядеть так:
x1 = vt1.
Подставив числа, получим: x1 = 36 км.
Путь S1 = vt1. Он также равен 36 км.
Расстояние L1 находим по формуле L1 = | хВ – х1 |, где
хВ – координата пункта В (в выбранной системе отсчета она равна L = 40 км). С учетом числовых значений L1 = 4 км.
В момент t = t2 x2 = vt2.
Подставив числа, получим: x2 = 108 км.
Путь S2 = vt2. Он также равен 108 км.
Расстояние L2 находим по формуле L2 = | хВ – х2 | (или наоборот, из х2 вычитаем хВ, разницы нет, поскольку берется модуль разности). С учетом числовых значений L2 = 68 км.
Решим эту же задачу, изменив направление оси на противоположное. Кроме того, изменим положение начала оси. Пусть оно теперь совпадает с пунктом В (рисунок b).
![]()
Рис. b
Вновь записываем уравнение движения тела в проекциях на ось Х:
x = x0 + vxt и находим проекции.
Начальная координата тела – это координата пункта А. В этой системе координат она равна L то есть x0 = хА = L. Проекция скорости vx = v Cos 1800 = – v. Тогда
x = L − vt.
В момент t = t1 x1 = L – vt1. Подставив числа, получим: x1 = 4 км.
Путь, пройденный телом за это время, S1 = vt1. S1 = 36 км. Расстояние L1 находим по формуле L1 = | хВ – х1 |. В данной системе координат хВ = 0, тогда
L1 = | 0 – х1 | = | – х1 |, то есть опять те же 4 км.
В момент t = t2 x2 = L – vt2. С учетом числовых значений x2 = – 68 км. Путь, пройденный телом за время t2, S2 = vt2. S2 = 108 км. Расстояние L2 находим по формуле L2 = | хВ – х2 |. = | – х2 |, то есть опять те же 68 км.
Таким образом, выбор направления оси и положения ее начала не оказывает влияния на конечный результат.
Ответ: L1 = 4 км, L2 = 68 км, S1 = 36 км, S2 = 68 км.
Задача 2. Из двух точек А и В, расположенных на расстоянии L = 90 метров друг от друга, одновременно в одном направлении начали движение два тела. Тело, движущееся из точки А, имело скорость, величина которой v1 = 5 м/с, а тело, движущееся из точки В, имело скорость, равную по величине v2 =2 м/с. Через какое время tвстр первое тело нагонит второе? На каком расстоянии Lвстр от пункта А произойдет их встреча? Найти расстояние L1 между телами спустя 50 секунд после начала движения.
Дано: L = 90 м, v1 = 5 м/с, v2 = 2 м/с, t1 = 50 с.
tвстр − ? Lвстр − ? L1 − ?
Решение.
![]()
Рис. a
Записываем кинематическое уравнение движения для каждого тела:
r1 = r01 + v1t, r2 = r02 + v2t или в проекциях на ось Х:
x1 = x01 + v1xt, x2 = x02 + v2xt. Находим проекции:
x01 = 0, v1x = v1 Cos 00 = v1, x02 = АВ,
v2x = v2 Cos 00 = v2. Тогда
x1 = v1t,
x2 = АВ + v2t.
В момент времени t = tвстр тела будут находиться в одной точке с координатой хвстр, то есть в точке С (рис. a). Тогда уравнения движения тел для этого момента времени будут выглядеть так:
для первого тела: хвстр = v1 tвстр, для второго тела:
хвстр = АВ + v2 tвстр.
Левые части двух последних уравнений равны между собой, значит, равны и правые части:
v1 tвстр = АВ + v2 tвстр, откуда
tвстр
=
 ,
tвстр
=
,
tвстр
=
 ,
tвстр
= 30 с.
,
tвстр
= 30 с.
Зная время встречи, можно найти и координату точки встречи, например, из уравнения движения первого тела (можно для этого воспользоваться и уравнением движения второго тела).
хвстр = 5∙30 м = 150 м, xС = 150 м, АС = 150 м.
Находим расстояние от места встречи до пункта А:
Lвстр = | xС – xА | = | АС – 0 | = АС, Lвстр = 150м.
Выразим в общем виде зависимость расстояния между движущимися телами от времени:
L = | x2 – x1 | = | (АВ + v2t) – v1t |, L = | АВ + (v2 − v1) t |. L = | 90 – 3t |.
По точкам строим график этой зависимости (рис. b).

Рис. b
В момент, когда t = t1, L1 = |90 – 3t1|.
L1 = |90 – 3∙50| м, L1 = | – 60 | м = 60 м.
Ответ: tвстр = 30 с, Lвстр = 150 м, L1 = 60 м.
Задача 3. По прямолинейному шоссе движутся равномерно в противоположных направлениях автобус и мотоциклист. В момент начала наблюдения координаты автобуса и мотоциклиста и модули их скоростей соответственно равны: x0a = 100 м, x0м = − 300 м, va = 20 м/с, vм = 10 м/с (см. рисунок). Написать уравнения движения автобуса и мотоциклиста. Найти положения этих объектов через t1 = 5c после начала наблюдения. В какой момент времени положение каждого из них совпадало с началом системы координат? Когда и где произошла их встреча? Каким будет расстояние L2 между ними через t2 = 1,5 мин после начала наблюдения? Построить графики зависимости от времени координат автобуса и мотоциклиста и расстояния между ними.
Дано: x0a = 100 м, x0м = −300 м, va = 20 м/с, vм = 10 м/с, t1 = 5c, t2 = 1,5 мин = 90 с.
ха = ха(t) − ? хм = хм(t) − ? ха1 − ? хм1 − ? t' − ? t'' − ? tвстр − ? xвстр − ? L2 − ?
Решение.
![]()
Рис. а
Записываем уравнения движения автобуса и мотоциклиста в векторной форме:
rа = r0а + vаt, rм = r0м + vмt. То же самое в проекциях на ось Х:
xа = x0а + vаxt, xм = x0м + vмxt. Пусть направление оси совпадает с направлением движения автобуса (рис. а). Находим проекции:
x0а = 100, vаx = vа Cos 00 = vа, x0м = − 300,
vмx = vм Cos 1800 = − vм. Тогда
xа = 100 + vаt, xа = 100 + 20 t.
xм = − 300 – vмt, xм = − 300 – 10 t.
В момент t = t1 уравнения движения будут выглядеть так:
x1а = 100 + 20 t1, x1а = (100 + 20∙5) м = 200 м.
x1м = − 300 – 10 t1, x1м = (− 300 − 10∙5) м = − 350 м.
В момент t = t' xа = x'а = 0, и уравнение движения автомобиля примет вид:
0 = 100 + 20 t', откуда t' = − 100/20 = − 5 с.
В момент t = t'' xм = x''м = 0, и уравнение движения мотоцикла примет вид:
0
= − 300 – 10 t'',
откуда t''
= −
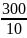 = − 30 с.
= − 30 с.
В момент встречи автомобиля и мотоцикла, когда t = tвстр, их координаты равны, то есть xа = xвстр, и xм = xвстр. Уравнения движения в этот момент времени будут выглядеть так:
для автомобиля xвстр = 100 + 20 tвстр, для мотоцикла xвстр = − 300 – 10 tвстр.
Поскольку левые части последних двух уравнений равны, то равны и правые части, то есть 100 + 20 tвстр= − 300 – 10 tвстр. Отсюда легко находим:
tвстр
= −
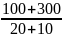 ,
tвстр
≈ − 13 с.
,
tвстр
≈ − 13 с.
Координату места встречи можно найти как из уравнения движения автомобиля, так и из уравнения движения мотоцикла для момента времени t = tвстр.
Для автомобиля: xвстр = 100 + 20∙(− 13). xвстр = − 160 м.
Расстояние L между объектами находим по формуле: L = | xа – xм |.
L = | xа – xм | = | (100 + 20 t) – (− 300 – 10 t) |, L = | 400 + 30 t |.
Для момента t = t2 L = L2 = | 400 + 30 t2 | = | 400 + 30∙90 |. L2 = 3100 м.
Чтобы построить графики зависимости от времени координат автобуса и мотоциклиста и расстояния между ними, используем уравнения:
xа = 100 + 20 t, xм = − 300 – 10 t. Тогда L = | 400 + 30 t |.
Задавая различные значения t, строим нужные графики (рис. b).

Рис. b
Ответ: xа = 100 + 20 t, xм = − 300 – 10 t, x1а = 200 м, x1м = −3 50 м, t' = − 5 с,
t'' = −3 0 с, tвстр = − 13 с, xвстр = − 160 м, L2 = 3100 м.
Задача 4. Тело движется равномерно по прямолинейному шоссе со скоростью, величина которой v =5 м/с и последовательно проходит через пункты А, В и С. Расстояние между А и В равно АВ = 80 км, расстояние между В и С равно ВС = 20 км. Сколько времени понадобится телу, чтобы пройти расстояния между А и В, А и С, В и С? Где будет находиться тело спустя 1 час, после прохождения пункта А? Как будет изменяться со временем расстояние между телом и пунктом С? Построить график зависимости изменения этого расстояния от времени. Где и на каком расстоянии от пункта А находилось тело за 15 минут до того момента, как оно поравнялось с этим пунктом?
Дано: v = 5 м/с; АВ = 80 км = 8∙104 м;
ВС = 20 км = 2∙104 м; t' = 1ч = 3600 с;
tD = − 15 мин = − 900 с.
t1 − ? t2 − ? t3 − ? x' − ? L = f(t) − ? xD − ? AD − ?
Решение.
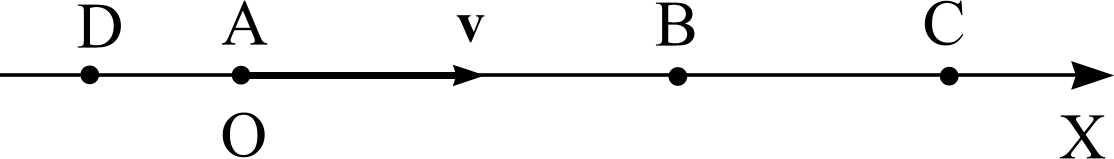
Рис. а
Записываем уравнение движения тела в векторной форме: r = r0 + vt. То же в проекциях на ось X (ось направляем от А к В и С, ее начало О совмещаем с пунктом А, как показано на рис. а):
x = x0 + vxt. Находим проекции:
x0 = 0, vx = v Cos 00 = v. x = vt. Отсчет времени ведем с момента прохождения телом пункта А. Для момента t = t1
x1
= vt1.
Но x1
= АВ, тогда АВ = vt1,
откуда t1
=
 .
Подставив числа, получим:
.
Подставив числа, получим:
t1 = 4∙103 с.
Для
момента t
= t2
x2
= vt2.
Но x2
= АС, тогда АC
= vt2,
откуда t2
=
 .
.
Подставив числа, получим: t2 = 5∙103 с.
Очевидно, что t3 = t2 − t1. t3 = 103 с.
В момент t = t' x' = vt.'
Подставив числа, найдем:
x' = 20∙3600 м = 72∙103м = 72км.
Расстояние между движущимся телом и пунктом С найдем по формуле:
L = | АС – x |. Так как x = vt, то L = | АС – vt | или
L = | 100 – 20t |.
По точкам строим график (рис. b).
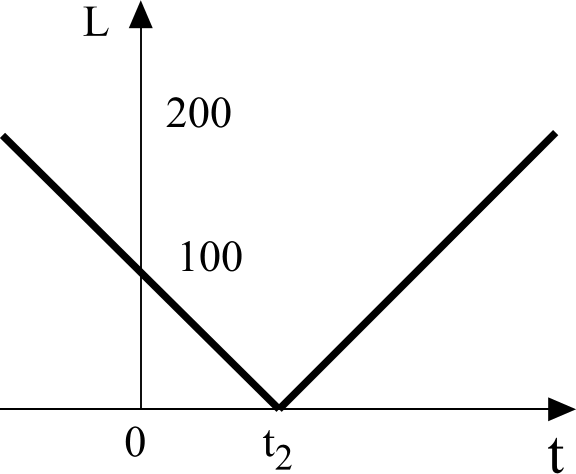
Рис. b
В момент t = tD xD = vtD.
Время tD отрицательно, поскольку нулевой момент времени мы выбрали, когда тело проходило через пункт А, а в пункте D тело побывало раньше.
tD = − 900 с, тогда xD = − 20∙900 м.
xD = − 18000 м = − 18 км. Находим расстояние AD:
AD = | xD − xА | = | − 18 – 0 | км = 18 км.
Ответ: t1 = 4∙103 с, t2 = 5∙103 с, t3 = 103 с, L = | 100 – 20t |, xD = − 18 км, AD = 18 км.
Задача 5. Торпеду выпускают из точки О, когда корабль противника находится в точке А, двигаясь со скоростью, величина которой vк = 50 км/ч и направленной под углом β = 300 к линии ОА (см. рисунок). Величина скорости торпеды vт = 100 км/ч. Под каким углом α ее надо выпустить, чтобы она поразила цель? Каково время t1 движения торпеды от момента ее выпуска до поражения цели? Расстояние между точками О и А 500 метров.
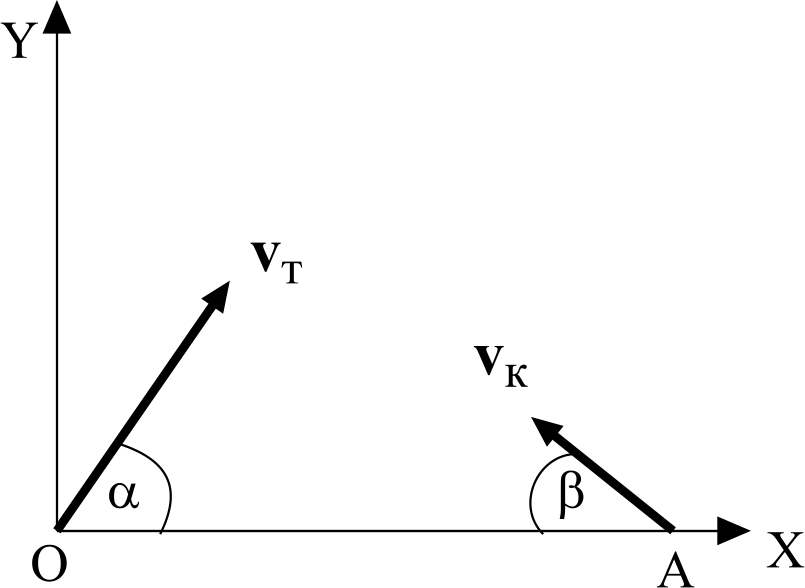
Рис. к задаче 11.1.5
Дано: vк = 50 км/ч = 14 м/с; β = 300;
vт = 100 км/ч = 28 м/с; ОО' = 500 м.
α − ? t1 − ?
Решение.
Запишем кинематические уравнения движения для торпеды и для корабля:
Для торпеды: rт = r0т + vтt.
Для корабля: rк = r0к + vкt.
Поскольку движение объектов происходит в плоскости (не вдоль одной прямой), то эти уравнения следует проектировать на две оси: на ось X и ось Y.
Для торпеды: xт = x0т + vтxt, yт = y0т + vтyt.
Для корабля: xк = x0к + vкxt, yк = y0к + vкyt.
Выбираем направления осей и начало системы отсчета. Пусть это будет так, как показано на рисунке.
Находим проекции. x0т = 0, vтx = vт Cos α, y0т = 0,
vтy = vт Cos (900 – α) = vт Sin α,
x0к = ОА, vкx = vк Cos (1800 – β) = – vк Cos β, y0к = 0, vкy = vк Cos (900 – β) = vк Sin β.
Подставив выражения для найденных проекций в кинематические уравнения, получим:
Для торпеды: xт = vт (Cos α)∙t, yт = vт (Sin α)∙t,
Для корабля: xк = ОА – vк (Cos β)∙t, yк = vк (Sin β)∙t.
В момент, когда торпеда попала в цель (t = t1), уравнения движения принимают вид:
Для торпеды: xт1 = vт (Cos α)∙t1,
yт1 = vт (Sin α)∙t1,
Для корабля: xк1 = ОА – vк (Cos β)∙t1,
yк1 = vк (Sin β)∙t1.
В этот момент времени (и только в этот, то есть, когда t = t1!) координаты объектов становятся равными, то есть xт1 = xк1, или
vт (Cos α)∙t1 = ОА – vк (Cos β)∙t1 и
vт (Sin α)∙t1 = vк (Sin β)∙t1. Из последнего равенства легко находим Sin α:
Sin
α = .
Подставив
числовые значения, получим Sin
α
= 0,25, откуда
.
Подставив
числовые значения, получим Sin
α
= 0,25, откуда
α = 14,50.
Из равенства координат по оси X:
vт (Cos α)∙t1 = ОА – vк (Cos β)∙t1.
Находим время встречи объектов:
t1
=
 .
.
Подставив числовые значения, получим t1 = 13 с.
Ответ: α = 14,50 , t1 = 13 с.
Задача 6. По прямолинейному участку шоссе движется автомобиль со скоростью, равной по величине vа = 54 км/ч. Пешеход находится на расстоянии b =80 м от шоссе и a =400 м от автомобиля. С какой минимальной по величине скоростью vп min он должен двигаться, чтобы встретить автомобиль, и сколько времени t1 он на это затратит? В каком направлении (по отношению к первоначальному направлению на автомобиль) пешеход при этом должен двигаться?
Дано: vа = 54 км/ч = 15 м/с; b = 80 м; а = 400 м;
vп min − ? t1 − ? α − ?
Решение.
Записываем кинематические уравнения движения автомобиля и пешехода:
rа = r0а + vаt, rп = r0п + vпt.
Поскольку движение объектов происходит в плоскости, то проектирование векторных уравнений движения необходимо выполнять на две оси. Пусть ось X направлена вдоль ОА, ось Y перпендикулярна оси X (см. рисунок). Начало координат выбрано в точке, где автомобиль находился в момент начала наблюдения.
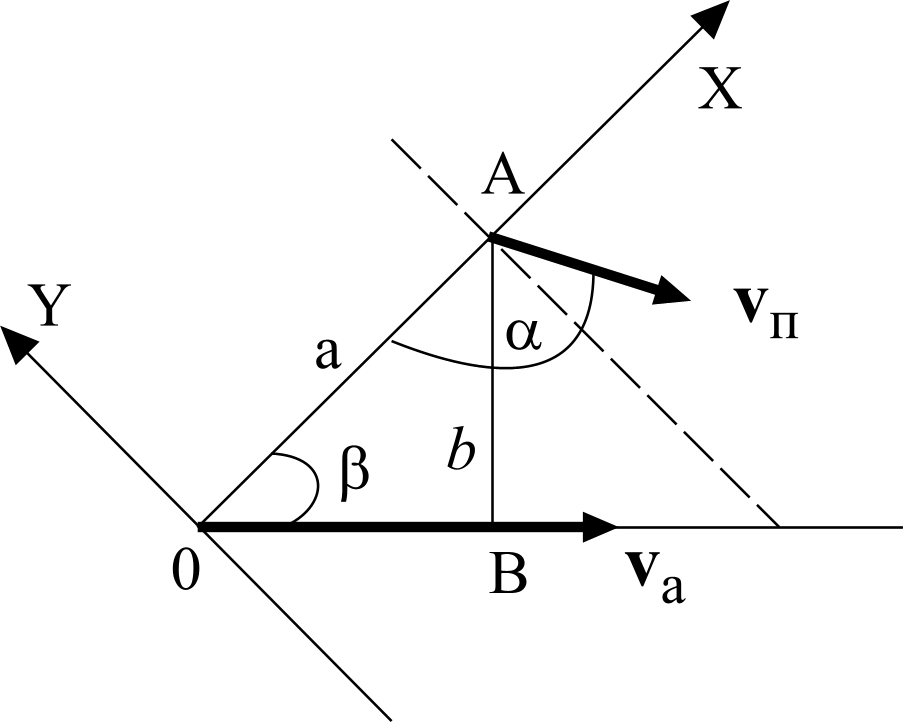
В проекциях на указанные оси уравнения движения будут выглядеть следующим образом.
Для автомобиля: xа = x0а + vаxt, yа = y0а + vаyt.
Для пешехода: xп = x0п + vпxt, yп = y0п + vпyt.
Находим проекции: x0а = 0, vаx = vа Cos β, y0а = 0,
vаy = vа Cos (900 + β) = − vа Sin β, x0п = а,
vпx = vп Cos (1800 − α) = − vп Cos α, y0п = 0,
vпy = vп Cos (2700 − α) = − vп Sin α.
Подставив выражения для найденных проекций в кинематические уравнения, получим:
Для автомобиля: xа = vа (Cosβ)∙t, yа = − vа (Sinβ)∙t.
Для пешехода: xп = а – vп (Cosα)∙t, yп = − vп (Sinα)∙t.
В момент встречи объектов, то есть когда t= t1, их уравнения движения будут выглядеть так:
Для автомобиля: xа1 = vа (Cosβ)∙t1,
yа1 = − vа (Sinβ)∙t1.
Для пешехода: xп1 = а – vп (Cosα)∙t1, yп1 = − vп (Sinα)∙t1.
В этот момент времени координаты автомобиля и пешехода будут одними и теми же, то есть xа1 = xп1 и
yа1 = yп1.
Из равенства координат по оси Y легко найти vп min. Действительно,
− vа
(Sin
β)∙t1
= − vп
(Sin
α)∙t1,
откуда vп
= vа
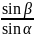 .
Проанализируем последнее выражение.
.
Проанализируем последнее выражение.
Когда vп будет иметь минимальное значение? Учитывая, что vа и Sin β в данной задаче являются величинами постоянными, несложно сделать вывод, что
vп = vп min, когда знаменатель дроби максимален. Знаменателем дроби является Sinα, а максимальное значение синуса – это единица. Таким образом, vп = vп min, когда Sin α = 1, то есть α = 900. Следовательно, vп min = vа Sin β. Учитывая, что
Sin
β
=
 ,
окончательно получим: vп
min
= vа
.
После подстановки числовых значений,
будем иметь: vп
min
= 3 м/с. Чтобы узнать время движения
пешехода, запишем равенство координат
объектов по оси X
в момент встречи:
,
окончательно получим: vп
min
= vа
.
После подстановки числовых значений,
будем иметь: vп
min
= 3 м/с. Чтобы узнать время движения
пешехода, запишем равенство координат
объектов по оси X
в момент встречи:
vа (Cos β)∙t1 = а – vп (Cos α)∙t1. Из этого выражения находим искомое время:
t1
=
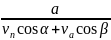 .
.
Это – самое общее выражение для t1, то есть, когда пешеход не ограничен условием нашей задачи. В этом общем случае ему не обязательно двигаться с
vп = vп min, он вправе идти или бежать с любой скоростью, однако, в этом случае, чтобы встретиться с автомобилем, направление движения пешехода должно быть уже другим. Это направление при заданной конкретной скорости пешехода находится из формулы vп = vа . Из этой формулы находим:
Sinα
=
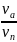 Sin
βп.
Sin
βп.
В нашем же случае условие задачи требует найти t1, когда vп именно равно vп min. Поскольку в этом случае α = 900, то Cos α = 0, и выражение для t1 упрощается:
t1
=
 Cos
β.
Из рисунка видно, что Cos
β
=
Cos
β.
Из рисунка видно, что Cos
β
=
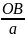 .
.
ОВ находим по теореме Пифагора:
ОВ
=
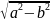 .
Тогда Cos
β
=
.
Тогда Cos
β
=
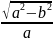 ,
и для t1
окончательно имеем: t1
=
,
и для t1
окончательно имеем: t1
=
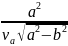 .
После подстановки числовых значений,
получим: t1
= 27 с.
.
После подстановки числовых значений,
получим: t1
= 27 с.
Ответ: vп min = 3 v/c, t1 = 27 с, α = 900.
Задача 7. Стержень АВ длиной L = 1 м опирается концами о пол и стену. Найти зависимость ординаты конца В от времени при движении конца А вдоль оси X с постоянной скоростью, равной по величине v = 0,3 м/с, от положения, указанного на рисунке (b = 0,6 м). Будет ли равномерным движение конца В? Найти величину скорости v'1 конца В, когда угол α' = 50 (см. рисунок).
Дано: L = 1 м; vА = 0,3 м/с; b = 0,6 м; α' = 50.
y = y (t) − ? v'1 −?
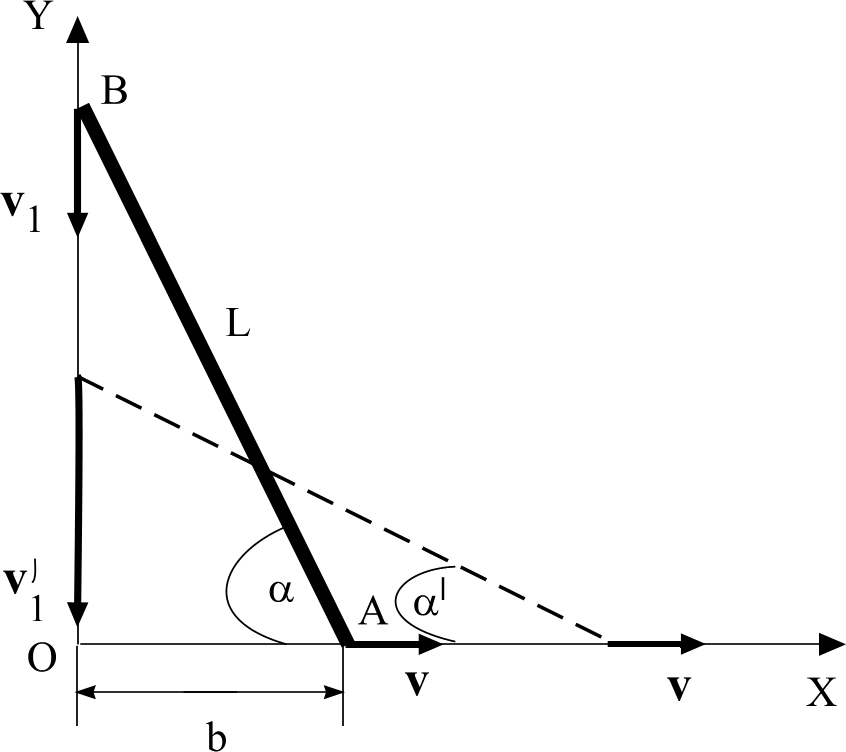
Решение.
Запишем кинематическое уравнение движения конца А стержня в проекциях на ось X (выбранные направления осей и начала системы координат показаны на рисунке).
x = x0 + vxt.
Находим проекции: x0 = b, vx = vА, тогда x = b + vt.
О движении конца В нам ничего не известно, кроме того, что он перемещается вдоль оси Y в сторону, противоположную направлению этой оси. Тем не менее, найти зависимость y = y (t) оказывается несложно, заметив, что для любого момента времени в соответствии с теоремой Пифагора
y
=
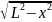 или y
=
или y
=
 .
Подставив числовые значения, окончательно
получим:
.
Подставив числовые значения, окончательно
получим:
y
=
 .
Это и будет ответом на первый вопрос
задачи.
.
Это и будет ответом на первый вопрос
задачи.
Найдем проекцию скорости конца В на ось Y. Для этого надо взять производную по времени от выражения y = .
v1y
=
 =
=
 .
Чтобы
найти модуль вектора по его проекции
(вспоминаем векторную алгебру), надо
извлечь корень квадратный из суммы
квадратов его проекций. У нас − одна
проекция: v1y.
Возводим правую часть последней формулы
в квадрат (знак минус при этом перейдет
в плюс) и извлекаем квадратный корень.
В результате получаем выражение для
модуля скорости:
.
Чтобы
найти модуль вектора по его проекции
(вспоминаем векторную алгебру), надо
извлечь корень квадратный из суммы
квадратов его проекций. У нас − одна
проекция: v1y.
Возводим правую часть последней формулы
в квадрат (знак минус при этом перейдет
в плюс) и извлекаем квадратный корень.
В результате получаем выражение для
модуля скорости:
v1
=
 .
Обратите внимание, что выражение в
числителе, стоящее в скобках, это есть
х, а знаменатель представляет собой y.
Таким образом, v1
=
.
Обратите внимание, что выражение в
числителе, стоящее в скобках, это есть
х, а знаменатель представляет собой y.
Таким образом, v1
=
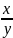 v.
В то же время
− это котангенс угла α
(см. рисунок). Поэтому v1
= v
Ctg
α.
v.
В то же время
− это котангенс угла α
(см. рисунок). Поэтому v1
= v
Ctg
α.
При движении стержня угол α меняется, поэтому будет меняться и модуль скорости v1.
Следовательно, движение конца В стержня не является равномерным, хотя оно и прямолинейное (в отличие от конца А, движение которого и равномерное и прямолинейное).
В
момент времени t
= t',
угол α
принимает значение α',
а скорость v1
становится
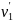 .
Тогда
= v
Ctg
α'.
Подставив числовые значения, получим:
.
Тогда
= v
Ctg
α'.
Подставив числовые значения, получим:
= 3,4 м/с.
Ответ: y = , = 3,4 м/с.
Задача 8. На наклонную плоскость, составляющую с горизонтом угол α, опирается стержень, который может перемещаться только по вертикали благодаря направляющему устройству. С какой по величине скоростью vст. поднимается стержень, если наклонная плоскость движется с постоянной скоростью, величина которой равна v?
Дано: α; v.
vст. − ?
Решение.
П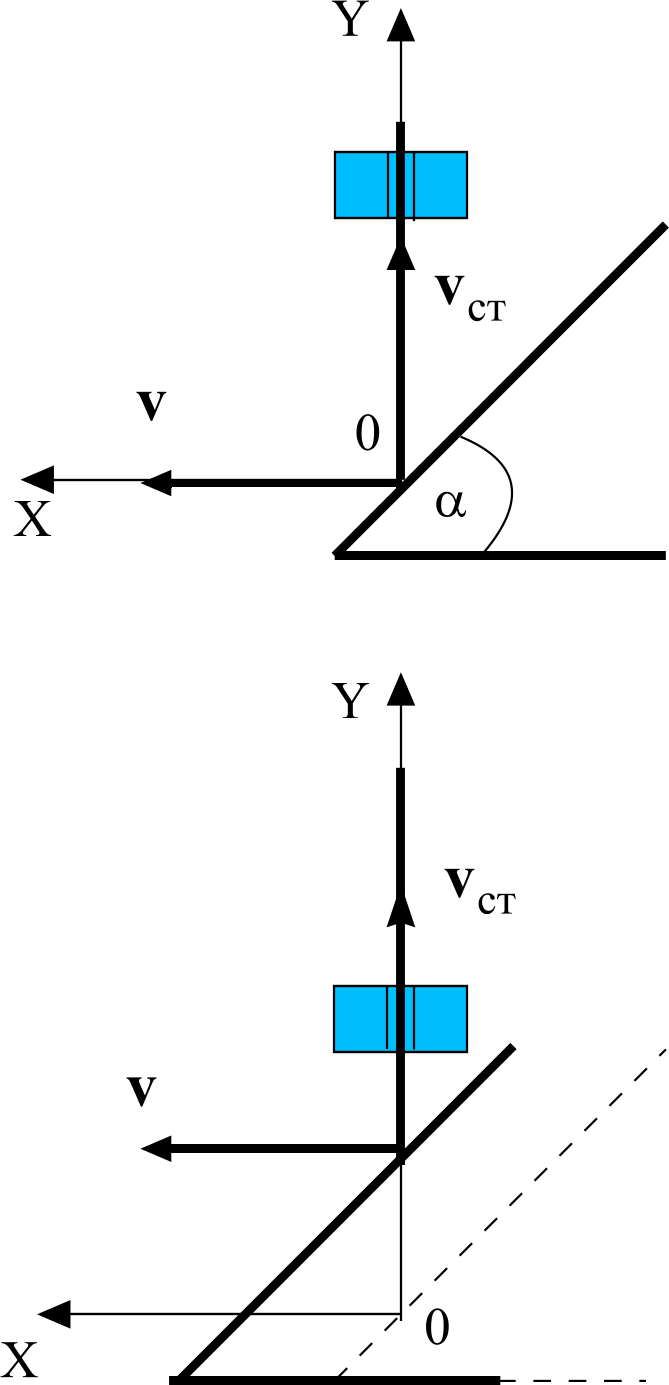 усть
мы начали наблюдение за плоскостью и
стержнем в момент, когда они находились
в положении, представленном на верхнем
рисунке. Там же показаны выбранные
направления осей и начало системы
координат. Положение объектов в следующий
(произвольный) момент времени показано
на нижнем рисунке (система отсчета
осталась той же, она у нас неподвижна!).
усть
мы начали наблюдение за плоскостью и
стержнем в момент, когда они находились
в положении, представленном на верхнем
рисунке. Там же показаны выбранные
направления осей и начало системы
координат. Положение объектов в следующий
(произвольный) момент времени показано
на нижнем рисунке (система отсчета
осталась той же, она у нас неподвижна!).
За прошедшее время плоскость сместилась по горизонтали, а стержень поднялся по вертикали (по горизонтали он не перемещается из-за направляющего устройства).
Запишем уравнения движения для объектов.
Для плоскости (точнее, для той ее точки, которая соприкасалась со стержнем в начальный момент времени):
x = x0 + vxt, y = 0. Находим проекции:
x0 = 0, vx = v Cos 00 = v. Тогда x = vt.
Для стержня: x = 0, y = y0 + vст.yt. Находим проекции: y0 = 0, vст.y = vст. Cos 00 = vст..
Тогда y = vст.t.
Из
нижнего рисунка видно, что
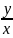 =
tg
α.
Это соотношение справедливо для любого
момента времени, поскольку два
рассмотренных фрагмента движения были
выбраны произвольно.
=
tg
α.
Это соотношение справедливо для любого
момента времени, поскольку два
рассмотренных фрагмента движения были
выбраны произвольно.
Тогда = tg
α,
откуда vст.
= v
tg
α.
= tg
α,
откуда vст.
= v
tg
α.
Ответ: vст. = v tg α.
Задача 9. Два автомобиля движутся по двум прямолинейным и взаимно перпендикулярным дорогам по направлению к перекрестку с постоянными скоростями, равными по величине v1 = 50 км/ч и v2 = 100 км/ч. Перед началом движения первый автомобиль находился на расстоянии L1 = 100 км от перекрестка, второй – на расстоянии L2 = 50 км. Через сколько времени t1 после начала движения расстояние между автомобилями будет минимальным? Каким будет это минимальное расстояние Lmin? Где при этом будут находиться автомобили?
Дано: v1 = 50 км/ч; v2 = 100 км/ч; L1 = 100 км; L2 = 50 км.
t1 − ? Lmin −? x'1 − ? y'2 − ?

Решение.
Начало системы отсчета совмещаем с центром перекрестка. Направления осей показаны на рисунке. Отсчет времени ведем от момента начала движения автомобилей.
Записываем уравнения движения автомобилей в проекциях на выбранные оси.
Для первого автомобиля: x1 = x01 + v1xt,
y1 = y01 + v1yt.
Для второго автомобиля: x2 = x02 + v2xt,
y2 = y02 + v2yt.
Находим проекции: = x01 = − L1, v1x = v1 Cos 00 = v1, y01 = 0, v1y = v1 Cos 900 = 0, x02 = 0,
v2x = v2 Cos 900 = 0, y02 = − L2, v2y = v2 Cos 00 = v2.
После подстановки получим: x1 = − L1 + v1t, y1 = 0,
x2 = 0, y2 = − L2 + v2t.
Для любого момента времени расстояние L между автомобилями определяется теоремой Пифагора:
L
=
 =
=
 .
.
В момент t = t1 расстояние между автомобилями будет минимальным, то есть
L = Lmin. Чтобы найти этот момент, надо взять производную от L по времени и приравнять ее нулю. Возьмем эту производную (для этого надо вспомнить, как берется производная от степенной функции и производная от сложной функции).
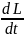 =
=
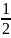 [
[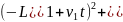 ]-1/2
∙ [2
]-1/2
∙ [2 )
)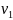 + + 2
)
+ + 2
)
=
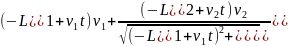
Теперь приравниваем эту производную нулю. Дробь равна нулю, когда ее числитель равен нулю.
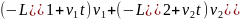 =
0. Отсюда легко находим время:
=
0. Отсюда легко находим время:
t
= t1
=
 .
Индекс единица в обозначении времени
(t1)
поставлен потому, что только в этот
момент времени (t
= t1)
производная равна нулю и L
= Lmin.
.
Индекс единица в обозначении времени
(t1)
поставлен потому, что только в этот
момент времени (t
= t1)
производная равна нулю и L
= Lmin.
Подставив числовые значения, найдем: t1 = 0,8 ч.
Выясним, где будут находиться автомобили в этот момент времени.
 =
− L1
+ v1t1,
y'2
= − L2
+ v2t1.
Подставив числа, получим:
=
− L1
+ v1t1,
y'2
= − L2
+ v2t1.
Подставив числа, получим:
=
− 60 км (первый автомобиль еще не доехал
до перекрестка),
 =
30 км (второй автомобиль уже прошел
перекресток).
=
30 км (второй автомобиль уже прошел
перекресток).
Найдем минимальное расстояние между автомобилями:
Lmin
=
 .
Подставив числа, получим:
.
Подставив числа, получим:
Lmin = 67 км.
Ответ: t1 = 0,8 ч, ℓmin = 67 км, = − 60 км, = 30 км.
Задача 10. Автомобиль, двигаясь со скоростью, величина которой v1 = 36 км/ч, проехал половину пути до места назначения за некоторый промежуток времени t1. С какой по величине скоростью v2 он должен продолжать движение, чтобы за такое же время достигнуть цели и вернуться обратно?
Дано: v1 = 36 км/ч; t1 = t2 + t3.
v2 − ?
Решение.
Имеются три участка, на которых автомобиль движется равномерно и прямолинейно:
1. Участок от начальной точки движения до середины пути (верхний рисунок). На этом участке скорость автомобиля v1, и проходит он его за какое-то время t1.
2. Участок от середины пути до конечной точки (средний рисунок). Здесь скорость автомобиля v2. Пусть t2 – время прохождения этого участка.
3. Участок от конечной точки до точки начала движения (нижний рисунок).

Здесь автомобиль движется со скоростью v3 (по условию задачи модули скоростей v2 и v3 одинаковы). Пусть t3 – время прохождения этого участка.
Запишем в проекциях на ось X кинематические уравнения движения автомобиля на каждом из этих участков. Направление оси и ее начало на каждом участке показано на рисунках.
Первый
участок:
 =
v1t1.
=
v1t1.
Второй участок: = v2t2.
Третий участок: L = v3t3 = v2t3, так как v2 = v3.
Сложим два последних уравнения:
+
L
= v2t2
+ v2t3
или
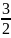 L
= v2
(t2
+ t3).
L
= v2
(t2
+ t3).
По
условию задачи t2
+ t3
= t1
Тогда
L
= v2t1.
Время t1
выразим из уравнения движения автомобиля
на первом участке: t1
=
 .
Подставив это выражение в предыдущее
уравнение, получим:
.
Подставив это выражение в предыдущее
уравнение, получим:
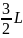 =
=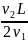 .
Отсюда легко находим искомую скорость:
v2
= 3 v1.
.
Отсюда легко находим искомую скорость:
v2
= 3 v1.
Ответ: v2 = 3 v1.
Задача 11. Первую половину своего пути автомобиль двигался со скоростью, равной по величине v1 = 80 км/ч, а вторую половину пути – со скоростью, величина которой v2 = 40 км/ч. Какова величина vср средней скорость движения автомобиля?
Дано: v1 = 80 км/ч; v2 = 40 км/ч; ∆S1 = ∆S2.
vср − ?
Решение.
Чтобы
не сделать ошибки в решении этой задачи
и подобных ей, надо иметь в виду следующее.
По определению vср
=
 и никак иначе! Поэтому, если тело за
время
и никак иначе! Поэтому, если тело за
время
∆t = ∆t1 + ∆t2 + … + ∆tN проходит путь
∆S = ∆S1 + ∆S2 + … + ∆SN, то средняя скорость пути находится по формуле:
vср
=
=
 ,
но никак не
,
но никак не
vср
=
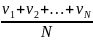 !
!
Возможен один частный случай, когда эта формула справедлива. Он будет рассмотрен ниже.
Итак,
решаем нашу задачу. vср
=
=
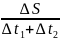 .
.
∆t1
=
 .
Но ∆S1
=
.
Но ∆S1
=
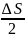 .
Тогда ∆t1
=
.
Тогда ∆t1
=
 .
Аналогично ∆t2
=
.
Аналогично ∆t2
=
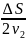 .
Следовательно,
.
Следовательно,
vср
=
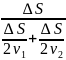 .
После несложных преобразований, получим:
vср
=
.
После несложных преобразований, получим:
vср
=
 .
Подставив числа, получим: vср
= 53 км/ч.
.
Подставив числа, получим: vср
= 53 км/ч.
Ответ: vср = 53 км/ч.
Задача 12. Первую половину времени своего движения автомобиль двигался со скоростью 80 км/ч, а вторую половину времени – со скоростью 40 км/ч. Какова средняя скорость движения автомобиля?
Дано: v1 = 80 км/ч; v2 = 40 км/ч; ∆t1 = ∆t2.
vср − ?
Решение.
vср
=
 ,
где ∆S1
– путь, пройденный телом за первую
половину времени ∆t1,
∆S2
– путь, пройденный телом за вторую
половину времени ∆t2.
,
где ∆S1
– путь, пройденный телом за первую
половину времени ∆t1,
∆S2
– путь, пройденный телом за вторую
половину времени ∆t2.
∆S1
= v1∆t1,
∆S2
= v2∆t2.
Но ∆t1
= ∆t2
=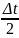 .
Тогда ∆S1
= v1
.
Тогда ∆S1
= v1
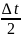 и ∆S2
= v2
.
Следовательно,
и ∆S2
= v2
.
Следовательно,
vср
=
 .
Окончательно vср
=
.
Окончательно vср
=
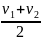 .
Подставив числа, получим:
.
Подставив числа, получим:
vср = 60 км/ч.
Ответ: vср = 60 км/ч.
Задача 13. Велосипедист проехал половину своего пути со скоростью, величина которой v1 = 12 км/ч. Затем половину оставшегося времени движения он ехал со скоростью, равной по величине v2 = 6 км/ч, а потом до конца пути шел пешком со скоростью, величина которой v3 = 4 км/ч. Определить величину vср средней скорости велосипедиста на всем пути.
Дано: v1 = 12 км/ч; v2 = 6 км/ч; v3 = 4 км/ч;
∆S1
= ∆S2
+ ∆S3;
∆t2
= ∆t3
=
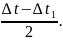
vср − ?
Решение.
По определению vср = . Весь путь ∆S состоит из трех участков: ∆S1, ∆S2 и ∆S3, поэтому
vср
=
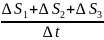 .
.
Путь первого участка ∆S1 = v1t1, где t1 – время прохождения первого участка.
Путь второго участка: ∆S2 = v2t2, где t2 – время прохождения второго участка.
Путь третьего участка: ∆S3 = v3t3, где t3 – время прохождения третьего участка.
По
условию ∆t2
= ∆t3
=
 ,
тогда
,
тогда
∆S2 = v2 , ∆S3 = v3 .
Формула для средней скорости принимает вид:
vср
=
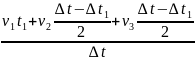 (1)
(1)
По условию также ∆S1 = ∆S2 + ∆S3 или
v1t1 = v2 + v3 . (2)
Осталось выразить из уравнения (2) ∆t1 и подставить в уравнение (1).
Из
(2): ∆t1
=

(элементарные преобразования опущены).
Подставив выражение для ∆t1 в уравнение (1), после простых, но нудных алгебраических преобразований (они тоже опущены), окончательно будем иметь:
vср
=
 .
.
Подставив числовые значения, получим:
vср = 7 км/ч.
Ответ: vср = 7 км/ч.
Движение с постоянным ускорением. Решение задач
Задача 1. Автомобиль, имея скорость, равную по величине v0 = 32,4 км/ч, за время t1 =22 с увеличил ее до значения v1 = 72 км/ч. Определить величину ускорения и путь, пройденный автомобилем за это время, считая движение равноускоренным.
Дано: v0 = 32, 4 км/ч = 9 м/c, t1 = 22 c, v1 = 72 км/ч = 20 м/с.

a − ? S1 − ?
Решение.
Записываем кинематическое уравнение и уравнение для скорости при движении с постоянным ускорением:
r
= r0
+ v0t
+ ,
v
= v0
+ at.
Проектируем
на выбранное направление оси X
(см. рисунок):
,
v
= v0
+ at.
Проектируем
на выбранное направление оси X
(см. рисунок):

x
= x0
+ v0xt
+
 .
vx
= v0x
+ axt.
.
vx
= v0x
+ axt.
Находим проекции: x0 = 0, v0x = v0∙Cos 00 = v0,
ax = a∙Cos 00 = a, vx = v∙Cos 00 = v. Тогда
x = v0t + ,
v = v0 + at.
Отсчет времени ведем с момента, когда скорость автомобиля была v0. В момент времени t1, то есть, когда автомобиль приобрел скорость v1, эти уравнения будут выглядеть так:
x1 = v0t1 + , (1)
v1 = v0 + at1 (2).
Из
уравнения (2) находим модуль ускорения:
a
=
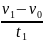 .
Подставляем числа, получаем:
.
Подставляем числа, получаем:
а = 0,5 м/с2.
Из уравнения (1) находим (после подстановки числовых значений) координату точки, в которой автомобиль имеет скорость v1: x1 = 319 м.
Перемещение автомобиля за промежуток времени t1 будет равно искомому пути S1, поскольку движение происходит вдоль прямой и в одну сторону (в противном случае величина перемещения и путь не совпадают).
S1 = | x1 – 0 | = | x1 |. S1 = 319 м.
Ответ: a = 0,5 м/с2, S1 = 319 м.
Задача 2. Посадочная скорость пассажирского самолета имеет величину v0 = 135 км/ч. Длина пробега L1 =500 м. Определить время t1 пробега по посадочной полосе и величину а ускорения самолета, считая движение равнозамедленным.
Дано: v0 = 135 км/ч = 37,5 м/c, v1 = 0, L1 = 500 м.
t1 − ? , a − ?
Решение.
Записываем кинематическое уравнение и уравнение для скорости при движении с постоянным ускорением:
r = r0 + v0t + , v = v0 + at. Проектируем на выбранное направление оси X (см. рисунок):
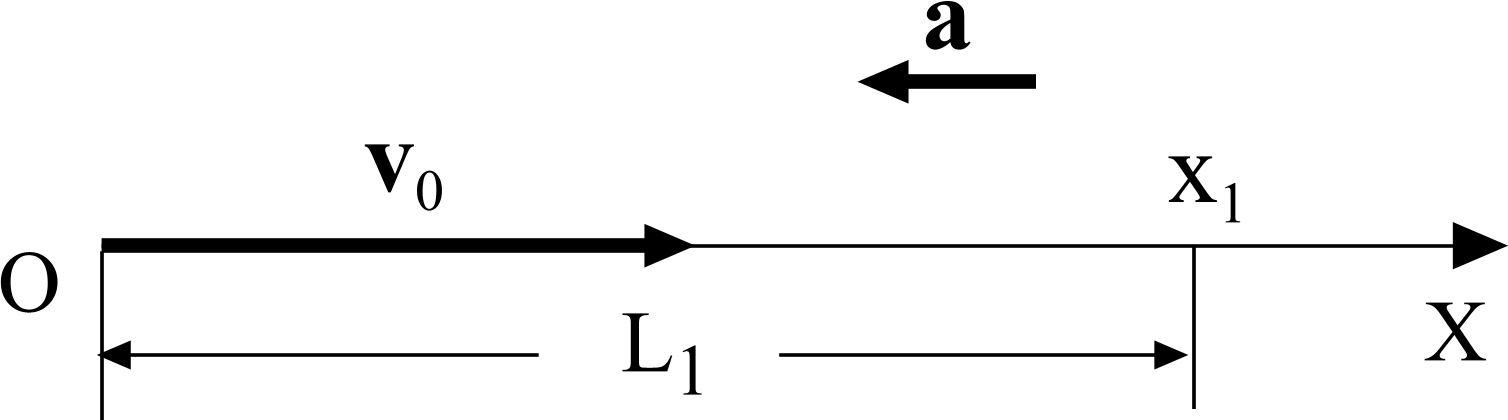
x = x0 + v0xt + . vx = v0x + axt.
Находим проекции: x0 = 0, v0x = v0∙Cos 00 = v0,
ax = a∙Cos 1800 = − a. Тогда
x = v0t − ,
vx = v0 − at.
Отсчет времени ведем с момента, когда скорость автомобиля была v0. В момент времени t1, то есть, когда самолет остановился, эти уравнения будут выглядеть так:
x1
= v0t1
−
 ,
,
v1x = v0 − at1. Но в этот момент x1 = L1, v1x = 0 (модуль скорости самолета равен нулю, значит, равна нулю и ее проекция). Тогда
L1 = v0t1 − , (1)
0 = v0 − at1. (2)
Получили систему из двух уравнения с двумя неизвестными (t1 и a). Выражаем модуль ускорения из второго уравнения и подставляем в первое.
В результате получаем (элементарные преобразования опущены):
a
=
 ,
L1
=
,
L1
=
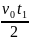 ,
откуда t1
=
,
откуда t1
=
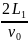 .
Подставляем числа и получаем: t1
= 27 с,
.
Подставляем числа и получаем: t1
= 27 с,
а = 1,4 м/с2.
Ответ: t1 = 27 с, а = 1,4 м/с2.
Задача 3. Два автомобиля движутся навстречу друг другу – первый равноускоренно с начальной скоростью, величина которой v01 = 36 км/ч и ускорением, равным по величине а1 = 0,3 м/с2, а второй – равнозамедленно с начальной скоростью, величина которой v02 = 54 км/ч и ускорением, равным по величине а2 = 0,5 м/с2. Найти время t', прошедшее с начала наблюдения до остановки второго автомобиля. Через какое время t1 автомобили встретятся, и какой путь от момента начала наблюдения до встречи пройдет каждый из них? Какую скорость будет иметь каждый автомобиль при встрече? Через какое время после начала наблюдения величины скоростей автомобилей окажутся равными? Найти зависимость расстояния между автомобилями от времени и построить график этой зависимости. Начальное расстояние между автомобилями 250 м.
Дано: v01 = 36 км/ч = 10 м/c, а1 = 0,3 м/с2,
v02 = 54 км/ч = 15 м/c, а2 = 0,5 м/с2, L0 = 250 м.
t' − ? t1 − ? t2 − ? s1 ? S1 − ? s2 ? S2 − ? vвст1 − ? Vвст1 − ?
vвст2 − ? Vвст2 τ − ? L = L(t) ?
Решение.
Записываем кинематические уравнения движения и уравнения для скорости при движении с постоянным ускорением для каждого автомобиля:
r1
= r01
+ v01t
+
 ,
v1
= v01
+ a1t,
,
v1
= v01
+ a1t,
r2
= r02
+ v02t
+
 ,
v2
= v02
+ a2t.
,
v2
= v02
+ a2t.
То же самое в проекциях на ось X:
x1
= x01
+ v01x
t +
 ,
v1x
= v01
x
+ a1xt,
,
v1x
= v01
x
+ a1xt,
x2
= x02
+ v02xt
+
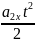 ,
v2x
= v02x
+ a2xt.
,
v2x
= v02x
+ a2xt.
Находим проекции (направление оси и ее начало показаны на рисунке a):

Рис. а
x01 = 0, v01x = v01 Cos 00 = v01, a1x = a1 Cos 00 = a1, x02 = L0,
v02x = v02 Cos 1800 = − v02, a2x = a2 Cos 00 = a2.
С учетом найденных проекций, имеем:
x1 = v01 t + ,
v1 = v01 + a1t,
x2 = L0 − v02t + ,
v2x = − v02 + a2t.
Далее можно решать задачу в общем виде, а можно уже сейчас подставить данные в условии числовые значения. В последнем случае решение несколько упростится. С учетом числовых значений, предыдущие четыре уравнения примут вид:
x1 = 10 t + 0,15 t2, (1)
v1 = 10 + 0,3 t, (2)
x2 = 250 − 15t + 0,25 t2, (3)
v2x = − 15 + 0,5 t. (4)
В момент t = t' второй автомобиль остановится и затем начнет движение в противоположную сторону. В момент остановки величина его скорости станет равной нулю. Значит и проекция скорости автомобиля тоже будет равна нулю, следовательно, в этот момент выражение (4) примет вид:
− 15 + 0,5 t' = 0, откуда t' = 30 с.
Найдем время встречи автомобилей. В общем случае автомобили в процессе своего движения могут или вообще не встретиться или встретиться два раза. Действительно, их первая встреча может произойти либо, когда второй автомобиль еще продолжает свое равнозамедленное движение в первоначальном направлении, либо, после того, как он остановился (не доехав до первого), повернул в противоположную сторону и, не набрав еще достаточной скорости, чтобы «убежать» от нагоняющего первого автомобиля, будет им настигнут. Вторая встреча может произойти после первой, если величина ускорения второго автомобиля больше первого: рано или поздно второй автомобиль после разворота разгонится до скорости большей, чем у первого и обгонит его. При каких условиях автомобили не встретятся вообще? Эта ситуация возможна, если второй автомобиль развернется до встречи с первым и успеет от него «удрать», имея большее по величине ускорение. Какая из перечисленных возможностей будет реализована в действительности – это зависит от числовых данных условия задачи. Посмотрим, что будет в нашем случае.
В момент встречи автомобилей их координаты станут одинаковыми, поэтому правые части выражений (1) и (3) будут равны друг другу:
10 t1,2 + 0,15 (t1,2)2 = 250 – 15 t1,2 + 0,25 (t1,2)2. Индексы 1,2 у времени поставлены потому, что это квадратное уравнение должно иметь два корня.
Приводим уравнение к виду
(t1,2)2 – 250∙t + 2500 = 0 и решаем его. В результате решения получим:
t1 = 10,4 с; t2 = 239,6 с.
Таким образом, автомобили встретятся дважды: первый раз до остановки второго автомобиля (он остановится спустя
t' – t = 30 – 10,4 = 19,6 с после встречи), а второй раз после того, как второй автомобиль развернется и догонит первый.
Теперь найдем пути, которые прошли автомобили от момента начала наблюдения до встречи. Поскольку, как мы выяснили, было две встречи, то речь должна идти о двух путях для каждого автомобиля.
Для первого автомобиля – все просто: он все время движется прямолинейно и в одну сторону. В этом случае его перемещение и путь численно совпадают. До первой встречи s1 = | (x1)1 − 0 |, где (x1)1 – это координата первого автомобиля в момент t = t1, то есть в момент первой встречи. Эту координату находим из (1):
(x1)1 = 10 t1 + 0,15 (t1)2. Подставляя числовое значение t1 (10,4 с), найдем:
(x1)1 = s1 = 120 м. Найдем путь, пройденный до второй встречи: S1 = | (x1)2 − 0 |, где (x1)2 – это координата первого автомобиля в момент t = t2, то есть в момент второй встречи.
Эту координату тоже находим из (1): (x1)2 = 10 t2 + 0,15 (t2)2. Подставляя числовое значение t2 (239,6 с), найдем:
(x1)2 = S1 = 11007 м.
Со вторым автомобилем немного сложнее, его движение, хотя и прямолинейное, но не всегда направлено в одну сторону. Поэтому, если рассматривается промежуток времени, в течение которого направление движения меняется, то путь, проходимый за это время уже не будет равен величине перемещения за этот промежуток времени. Чтобы найти этот путь, надо сложить величины перемещений, совершенных автомобилем при движении только в одну сторону.
Второй автомобиль двигался в одну сторону (противоположно направлению оси X) от момента начала наблюдения до остановки. В этом случае его путь
А = | L0 – x' |, где x' – это координата второго автомобиля в момент t = t', то есть в момент остановки автомобиля. Эту координату найдем из (3):
x' = 250 – 15 t' + 0,25 (t')2. Подставляя числовое значение t' (30 с), найдем:
x' = 25 м. Тогда s' = | 250 – 25 | м. s' = 225 м. После мгновенной остановки автомобиль продолжает движение, но уже в противоположном направлении (теперь он движется по направлению оси X). Найдем путь B, пройденный вторым автомобилем на участке от остановки до первой встречи с первым автомобилем:
B = | (x2)1 − x' |, где (x2)1 − это координата второго автомобиля в момент t = t1, то есть в момент первой встречи. Но она равна (x1)1, то есть 120 м.
Тогда B = | 120 – 25 | м = 95 м. Окончательно, путь второго автомобиля от начала наблюдения до первой встречи с первым автомобилем
s2 = A + B = 225 + 95 = 320 м.
Чтобы найти путь S2 второго автомобиля от начала наблюдения до второй встречи с первым, надо к пути A (от начала наблюдения до остановки) прибавить путь C, пройденный вторым автомобилем от остановки до второй встречи. Найдем C: C = | (x2)2 – x' |, где (x2)2 – это координата второго автомобиля в момент t = t2, то есть в момент второй встречи. Но она равна (x1)2, то есть 11007 м. Тогда
C = | 11007– 25 | м = 10982 м. Окончательно,
S2 = A + C = (225 + 10982) м = 11207 м.
Рисунок b качественно иллюстрирует предыдущие рассуждения.
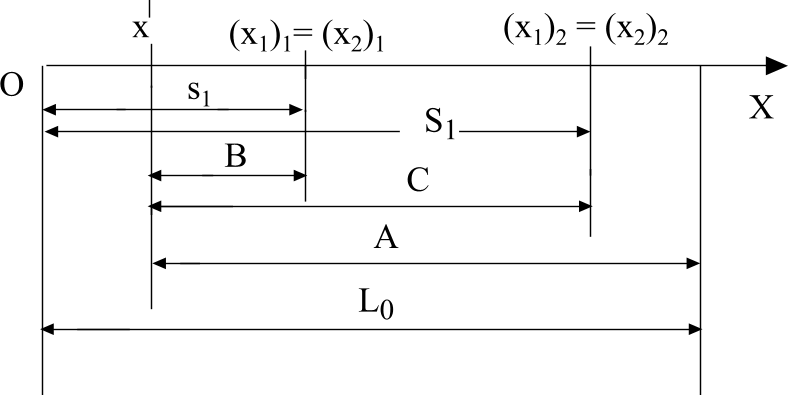
Рис. b
Теперь найдем скорость vвст1 первого автомобиля в момент первой встречи. Для этого привлекаем уравнение (2), записанное для момента t1 = t1: vвст1 = 10 + 0,3 t1. Подставляя числовое значение (t1 = 10,4 с), получим: vвст1 = 13,1 м/с. Аналогично, в момент второй встречи Vвст1 = 10 + 0,3 t2. Подставляя числовое значение
(t2 = 239,6 с), получим: Vвст1 = 72 м/с.
Точно также поступаем для нахождения скоростей второго автомобиля в моменты первой и второй встреч, но только используем уже уравнение (4).
vвст2x = − 15 + 0,5 t1 = −15 + 0,5∙10,4 = – 98 м/с. Проекция получилась отрицательная. Это и понятно, второй автомобиль в это время двигался в сторону, противоположную направлению оси Х.
Модуль этой скорости находим по известному правилу векторной алгебры:
vвст2
=
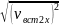 .
Подставляем и получаем: vвст2
= 98 м/с.
.
Подставляем и получаем: vвст2
= 98 м/с.
В момент второй встречи Vвст2x = − 15 + 0,5 t2 = − 15 + 0,5∙239,6 = 105 м/с.
Vвст2 = 105 м/с. Конечно, для обычного автомобиля это уж очень большая скорость и можно было бы взять другие числовые значения в условии данной задачи, чтобы привести полученные значения в соответствие с реальными скоростями. Но, не будем обращать на это внимание, пусть это будут автомобили будущего.
Найдем время τ (читается, тау), спустя которое скорости автомобилей сравняются. Анализируя числовые данные условия задачи, легко сообразить, что выравнивание скоростей произойдет дважды. Действительно, начальная скорость первого автомобиля 10 м/с, и он разгоняется, а начальная скорость второго автомобиля 15 м/с, и он до своей остановки замедляет свое движение. Понятно, что одну и ту же по модулю скорость автомобили приобретут еще до остановки второго автомобиля, и величина этой скорости будет больше 10 м/с и меньше
15 м/с. Второй раз скорости сравняются после того, как второй автомобиль изменит свое движение и будет догонять первый.
Для решения вопроса нам надо использовать уравнения (2) и (4). Но эти уравнения определяют проекции скоростей, нас же интересуют их модули.
С первым автомобилем проблем нет, он всегда движется в сторону положительного направления оси Х, и его проекция всегда равна модулю.
У второго же автомобиля проекция меняет свой знак: до остановки она отрицательна, а после остановки становится положительной, и в общем случае, то есть в течение всего времени движения второго автомобиля, мы не можем считать, что проекция его скорости равна модулю. Поэтому приравнивать правые части уравнений (2) и (4) мы не можем. Что же делать? Ведь кроме этих уравнений нам надеяться не на что. Надо возвести оба уравнения в квадрат, и приравнять правые части. Так мы разом избавимся от неопределенностей, связанных со знаками проекций скорости второго автомобиля. Сделаем это.
(10 + 0,3 τ1,2)2 = (− 15 + 0,5 τ1,2)2. Надеюсь, понятно, почему у τ стоят два нижних индекса: мы будем решать квадратное уравнение, которое имеет два корня. Один корень определяет время, когда модули скоростей станут одинаковыми до остановки второго автомобиля, а второй – после. Возведя в квадрат и приведя подобные члены, получим уравнение: 0,16 t2 – 21 t + 125 = 0. В результате решения будем иметь:
τ1 = 6,25 с, τ2 = 125 с. Конкретные значения величин скоростей можно узнать, если подставить τ1 и τ2 в уравнения (2) или (4). Удобнее − в уравнение (2), так как в этом случае мы сразу найдем модуль скорости.
Чтобы не путаться, обозначим модуль этой скорости, одинаковый как для первого, так и для второго автомобилей, как Vравн.
Vравн1 = 10 + 0,3 τ1 = 10 + 0,3∙6,25 = 12 м/с. Это – до остановки второго автомобиля.
Vравн2 = 10 + 0,3 τ2 = 10 + 0,3∙125 = 47,5 м/с. Это – после остановки второго автомобиля.
И, наконец, найдем зависимость расстояния L между автомобилями от времени.
Очевидно, что L = | x2 – x1 | (или наоборот). Используя уравнения (3) и (1), получим:
L = | (250 – 15 t + 0,25 t2) – (10 t + 0,15 t2) |. Раскрываем скобки, приводим подобные члены и получаем:
L = | 0,1t2 – 25 t + 250 |. Задавая времени различные числовые значения, строим график. Сделаем краткий анализ графика (рис. с).

Рис. с
Участок 1-2. На временном интервале, соответствующем этому участку, автомобили движутся навстречу друг другу. Точка 1 – начало наблюдения за машинами, в этот начальный момент времени расстояние между автомобилями 250 м. Точка 2 соответствует моменту встречи автомобилей (t1 = 10,4 с), расстояние между ними равно нулю.
Участок 2-3. В течение времени, соответствующего этому участку, вторая машина продолжает двигаться в том же направлении, что и раньше, но затем останавливается (в момент t' = 30 с от начала наблюдения), разворачивается и устремляется за первой машиной, все увеличивая свою скорость. В момент, соответствующий точке 3 графика (τ2 = 125 с от начала наблюдения), скорость второго автомобиля сравнялась со скоростью первого. После этого расстояние между автомобилями начнет уменьшаться.
Участок 3-4. Здесь второй автомобиль неуклонно нагоняет первый. В любой момент времени его скорость больше скорости первого автомобиля. Наконец (точка 4, и соответствующее ей время t2 = 239,6 с), второй автомобиль поравнялся с первым, и мгновенье спустя показал ему свой «хвост».
Участок 4-5. Водитель первого автомобиля с тоской наблюдает обогнавший его и постоянно удаляющийся второй автомобиль.
Ответ: t' = 30 с, t1 = 10,4 с; t2 = 239,6 с, s1 = 120 м, S1 = 11007 м, s2 = 320 м,
S2 = 11207 м, vвст1 = 13,1 м/с, Vвст1 = 72 м/с, vвст2 = 98 м/с, Vвст2 = 105 м/с,
τ1 = 6,25 с, τ2 = 125 с
Задача 4. При равноускоренном прямолинейном движении из состояния покоя тело за пятую секунду проходит путь ∆S5 = 1 м. Определить путь ∆S7, который проходит тело за седьмую секунду. Какую скорость v10 будет иметь тело в конце десятой секунды своего движения?
Дано: v0 = 0, ∆S5 = 1 м.
∆S7 − ? v10 − ?
Решение.
Записываем кинематическое уравнение движения и уравнение для скорости при движении с постоянным ускорением:
r1 = r0 + v0t + , v = v0 + at.
То же самое в проекциях на ось X:
x = x0 + v0x t + , vx = v0 x + axt.
Направление оси Х выбираем в сторону движения тела. Начало оси совмещаем с точкой, откуда тело начало двигаться.
Отсчет времени начинаем с момента начала движения. Тогда x = , v = at, поскольку x0 = 0, v0 = 0, ax = а, vx = v.
Так как тело всегда движется прямолинейно и в одну сторону, то модуль вектора перемещения равен пути, проходимому телом, то есть r = S или ∆r = ∆S. За пятую секунду тело совершит перемещение ∆r5 = x5 – x4 или
∆S5
= x5
– x4.
Но x5
= ,
x4
=
,
x4
=
 .
.
Тогда
∆S5
=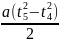 .
Отсюда найдем ускорение (оно нам
понадобится):
.
Отсюда найдем ускорение (оно нам
понадобится):
а
=
 .
.
Так
как t5
= 5 с, t4
= 4 с, то
 =
9 с2,
и а =
=
9 с2,
и а =
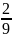 ∙∆S5.
Поскольку ∆S5
= 1 м, то
∙∆S5.
Поскольку ∆S5
= 1 м, то
а
=
 .
.
За седьмую секунду тело совершит перемещение
∆r7
= x7
– x6
или ∆S7
= x7
– x6.
Но x7
=
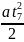 ,
x6
=
,
x6
=
 .
Тогда
.
Тогда
S7
=
 .
Учитывая, что t7
= 7 с, t6
= 6 с, а =
,
после подстановки получим: ∆S7
= 1, 4 м.
.
Учитывая, что t7
= 7 с, t6
= 6 с, а =
,
после подстановки получим: ∆S7
= 1, 4 м.
Величину скорости в конце десятой секунды найдем по формуле: v10 = at10. Подставляя числовые значения, получим:
v10
=
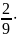 10
м/с = 2, 2 м/с.
10
м/с = 2, 2 м/с.
Ответ: ∆S7 = 1, 4 м, v10 = 2, 2 м/с.
Задача 5. Тело, имея начальную скорость, величина которой v0 = 5 м/с, прошло за пятую секунду путь, равный ∆S5 = 4,5 м. Определить величину а ускорения и путь ∆S60, пройденный телом за время t60 = 60 c, считая его движение прямолинейным и равнопеременным.
Дано: v0 = 5 м/с, ∆S5 = 4,5 м, t60 = 60 c.
а − ? ∆S60 − ?
Решение.
Записываем кинематическое уравнение движения и уравнение для скорости при движении с постоянным ускорением:
r1 = r0 + v0t + , v = v0 + at.
То же самое в проекциях на ось X:
x = x0 + v0x t + , vx = v0 x + axt.
Направление оси Х выбираем в сторону первоначального движения тела. Начало оси совмещаем с точкой начала наблюдения (см. рисунок).

Тогда x = v0∙t + , (1)
vх = v0 + aхt, (2)
поскольку x0 = 0, v0х = v0.
Найдем ускорение тела. За пятую секунду тело совершит перемещение, модуль которого ∆r5 = x5 – x4, где x4 – координата тела в конце четвертой (или, что то же самое, в начале пятой) секунды, x5 – координата тела в конце пятой (или, что то же самое, в начале шестой) секунды.
Но
x5
= v0∙t5
+
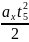 ,
x4
= v0∙t4
+
,
x4
= v0∙t4
+
 .
.
Тогда ∆r5 = v0∙t5 + − v0∙t4 − . Поскольку ∆r5 = ∆S5 (движение по прямой и в одну сторону), то
∆S5 = v0∙t5 + − v0∙t4 − . Отсюда найдем aх:
ах
=
 .
Подставив числовые значения, будем
иметь:
.
Подставив числовые значения, будем
иметь:
ах
= − 0,1 м/с2.
Модуль ускорения найдем по известной
формуле векторной алгебры: а =
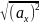 .
Получаем:
.
Получаем:
а = 0,1 м/с2.
Поскольку ах = − 0,1 м/с2, уравнения (1) и (2) примут вид: x = v0∙t − , (3)
vх = v0 – at. (4)
Получается, что тело движется равнозамедленно, поскольку вектор ускорения направлен противоположно направлению оси Х, то есть противоположно первоначальному направлению движения. Однако, спустя какое-то время t1, тело остановится и повернет вспять. Тогда направление движения тела и его ускорение совпадут, и движение станет равноускоренным.
Теперь найдем путь, пройденный телом за 60 с своего движения. Для этого нам следует воспользоваться кинематическим уравнением движения. Однако здесь мы должны проявлять осторожность. Дело в том, что это уравнение определяет зависимость от времени радиус-вектора тела (или вектора перемещения), но не пути! Модуль вектора перемещения и путь совпадают только лишь в том случае, когда тело движется прямолинейно и только в одну сторону. В нашем случае движение прямолинейное, но заранее мы не знаем, будет ли тело в течение 60 секунд двигаться в одну сторону, или остановится и повернет назад. Чтобы это узнать, следует выяснить, сколько времени t1 тело будет двигаться до остановки. Воспользуемся уравнением (4). В момент остановки скорость тела станет равной нулю, и уравнение (4) примет вид:
0
= v0
–
at1,
откуда t1
=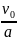 .
Подставив числовые значения, получим:
t1
=
.
Подставив числовые значения, получим:
t1
=
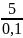 с = 50 с.
с = 50 с.
Итак, вначале тело движется равнозамедленно, через 50 с после начала наблюдения останавливается и, мгновенно развернувшись, начинает свое равноускоренное движение в противоположном направлении.
Тогда ∆S60 = ОА + АВ (см. рисунок). На каждом из участков (ОА и АВ) тело движется в одну сторону и для их нахождения мы можем использовать кинематическое уравнение движения. ОА = хост – 0 = хост. Из уравнения (3)
хост = v0∙t1 – . Тогда ОА = v0∙t1 – . Подставив числовые значения, получим:
ОА = 125 м.
АВ = хост – х60. Почему не наоборот?
Надо помнить, что АВ – это путь, а путь – это всегда положительный скаляр. А у нас при данном выборе системы координат хост > х60. Можно было бы записать и по-другому: АВ = | х60 – хост |.
х60
= v0∙t60
–
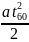 ,
где t60
= 60 с. Подставив числовые значения,
получим:
,
где t60
= 60 с. Подставив числовые значения,
получим:
х60 = 120 м.
Тогда АВ = (125 –120) м = 5 м.
∆S60 = ОА + АВ = (125 + 5) м = 130 м.
Ответ: а = 0,1 м/с2, ∆S60 = 130 м.
Задача 6. Два тела, 1 и 2, движутся вдоль прямой с ускорениями, модули которых соответственно равны а1 = 1 м/с2, а2 = 3 м/с2. Некоторую точку А второе тело проходит спустя τ = 14 с после первого в том же направлении. В точке А величина скорости первого тела vA = 22 м/с, величина скорости второго тела uA = 10 м/с. Через сколько времени t1 после прохождения первым телом точки А, оба тела встретятся? Какую по величине скорость u0 имело второе тело, и где оно находилось в момент времени, когда первое тело поравнялось с точкой А?
Дано: а1 = 1 м/с2, а2 = 3 м/с2, τ = 14 с, vA = 22 м/с, uA = 10 м/с.
t1 − ? u0 − ? х20 − ?
Решение.
Записываем кинематическое уравнение движения и уравнение для скорости для каждого тела при движении с постоянным ускорением:
r1 = r10 + v0t + , v = v0 + a1t,
r2 = r20 + u0t + , u = u0 + a2t.
То же самое в проекциях на ось X:
х1 = х10 + v0хt + , vх = v0х + a1хt,
х2 = х20 + u0хt + , uх = u0х + a2хt.
Направление оси Х выбираем так, как показано на рисунке. Начало оси совмещаем с точкой А. За начало отсчета времени выбираем момент, когда первое тело проходит точку А.

Находим проекции. х10 = 0, v0х = v0 = vA, a1х = a1, vх = v, a2х = a2.
Тогда
х1 = vАt + , (1)
v = vА + a1t, (2)
х2 = х20 + u0хt + , (3)
uх = u0х + a2t. (4)
Где находилось второе тело в начальный момент времени, то есть его начальную координату х20 мы пока не знаем. Также мы ничего пока не знаем о u0х: ведь второе тело в начальный момент времени не обязательно должно было двигаться в том направлении, как оно двигалось в точке А. За промежуток времени τ, отделяющий второе тело от начала наблюдения до того момента, когда оно проходило через точку А, второе тело вполне могло изменить направление своего движения. В момент начала наблюдения начальная скорость u0 могла быть направлена в сторону, противоположную направлению u в точке А и направлению a2. То есть в течение какого-то времени в пределах τ второе тело могло двигаться равнозамедленно, остановиться, мгновенно развернуться и продолжить свое движение в направлении оси Х и в направлении a2. Понятно, что после остановки движение второго тела станет уже равноускоренным.
Выражение для u0х найдем из (4), записанного для момента t = τ. В этот момент времени проекция скорости на ось Х равна uA. Тогда uА = u0х + a2∙τ, откуда
u0х = uА − a2∙τ. (5)
Подставив числа, получим: u0х = − 32 м/с. Таким образом, в момент начала наблюдения второе тело двигалось в направлении, противоположном тому, которое второе тело имело в точке А. Модуль этой скорости u0 = 32 м/с.
Из уравнения (3) найдем начальную координату второго тела, то есть х20. Для этого надо учесть, что в момент τ это тело находилось в точке с нулевой координатой, то есть в точке А (или в точке О). Для этого момента времени уравнение (3) примет вид:
0
= х20
+ u0х
τ
+
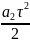 или 0 = х20
+ (uА
− a2∙τ)∙τ
+
,
откуда после элементарных преобразований
или 0 = х20
+ (uА
− a2∙τ)∙τ
+
,
откуда после элементарных преобразований
х20 = − uА∙τ + . (6)
Подставив числовые значения, получим: х20 = 154 м, то есть в момент начала наблюдения второе тело находилось справа от точки А и двигалось навстречу первому телу, которое в этот (начальный) момент времени проходило эту точку.
Подставив (5) и (6) в (3), запишем кинематическое уравнение движения второго тела:
х2 = (− uА∙τ + ) + (uА − a2∙τ)∙t + . После элементарных преобразований
х2
= uA
(t
– τ)
+
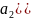 (7)
(7)
В момент встречи двух тел, то есть когда t = t1, их координаты совпадут. Тогда левые, а, значит, и правые части уравнений (1) и (7) будут равны друг другу:
vАt1
+
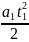 = uA
(t1
– τ) +
.
После
простых преобразований и подстановки
числовых значений приводим уравнение
к виду:
= uA
(t1
– τ) +
.
После
простых преобразований и подстановки
числовых значений приводим уравнение
к виду:
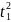 –
54 t1
+ 154 = 0. Решая это квадратное уравнение,
находим его корни: t1
= 51 c,
–
54 t1
+ 154 = 0. Решая это квадратное уравнение,
находим его корни: t1
= 51 c,
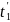 =
3 с. Первый корень (t1
> τ)
соответствует встрече тел после того,
как они прошли точку А и движутся в одном
направлении. Второй корень (
< τ)
соответствует встрече тел, когда второе
тело движется к точке А навстречу
первому.
=
3 с. Первый корень (t1
> τ)
соответствует встрече тел после того,
как они прошли точку А и движутся в одном
направлении. Второй корень (
< τ)
соответствует встрече тел, когда второе
тело движется к точке А навстречу
первому.
Ответ: t1 = 51 c, = 3 с, u0 = 32 м/с, х20 = 154 м.
Задача 7. Тело брошено с поверхности земли вертикально вверх с начальной скоростью, равной по величине v0. Найти: время t1 достижения телом максимальной высоты подъема, максимальную высоту H подъема, время t2 всего движения тела, то есть от момента бросания до момента падения на землю, величину скорости v2, с которой тело упало на землю.
Дано: v0.
t1 − ? H − ? t2 − ? v2 − ?
Решение.
Записываем кинематическое уравнение движения и уравнение для скорости тела при движении с постоянным ускорением:
r
= r0
+ v0t
+
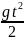 ,
v
= v0
+ gt.
,
v
= v0
+ gt.
То же самое в проекциях на ось Y:
y
= y0
+ v0yt
+
 ,
vy
= v0y
+ gyt.
,
vy
= v0y
+ gyt.
Направление оси Y выбираем по вертикали вверх. Начало оси совмещаем с точкой бросания (см. рисунок).
За начало отсчета времени выбираем момент бросания.
Находим проекции: y0 = 0, v0y = v0, gy = − g.
Тогда
y = v0t − , (1)
vy = v0 – gt. (2)
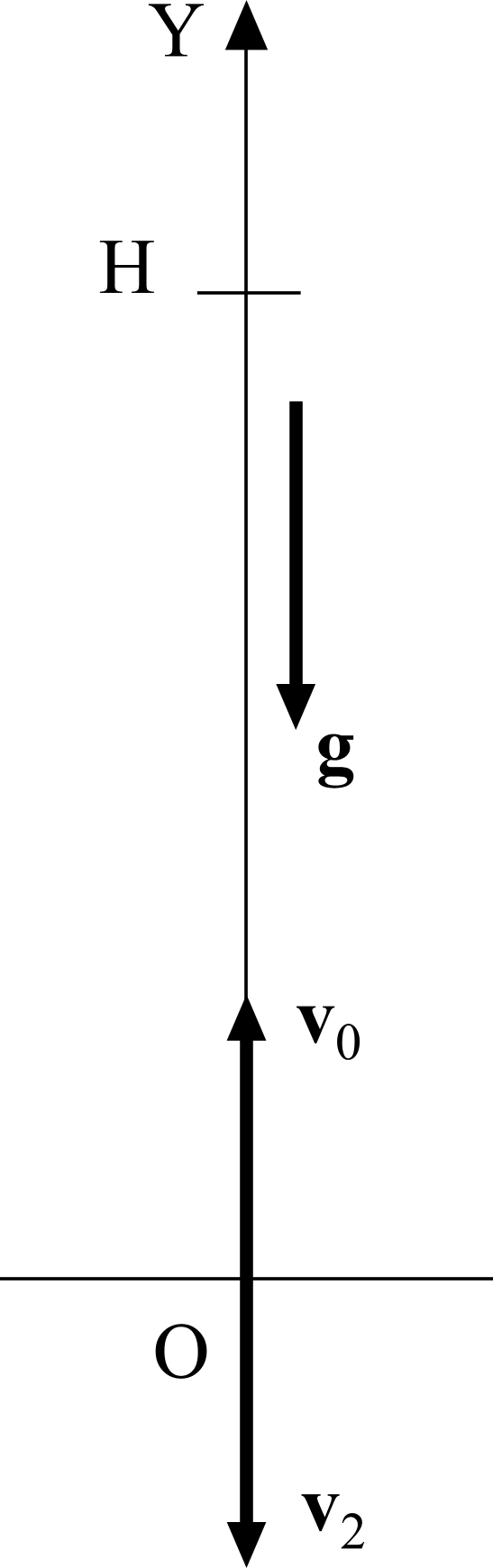
Когда тело достигнет высшей точки подъема, оно на мгновение остановится, а затем начнет падать вниз. В момент остановки, то есть когда t = t1, модуль скорости v1 тела равен нулю. Нулю будет равна и проекция этой скорости. Тогда уравнение (2) примет вид:
0
= v0
– gt1,
откуда t1
= .
В этот же момент времени уравнение (1)
будет выглядеть так:
.
В этот же момент времени уравнение (1)
будет выглядеть так:
y1
= v0t1
–
 .
Но y1
= H,
тогда H
= v0t1
–
.
С учетом найденного выражения для t1,
получим: H
= v0∙
– g∙
.
Но y1
= H,
тогда H
= v0t1
–
.
С учетом найденного выражения для t1,
получим: H
= v0∙
– g∙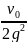 .
Окончательно H
=
.
Окончательно H
=
 .
.
Когда
тело упало на землю (в момент t
= t2),
его координата стала равна нулю. Тогда
уравнение (1) примет вид: 0 = v0t2
–
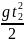 ,
откуда t2
=
,
откуда t2
=
 .
.
Сравнивая полученную формулу с выражением для t1, делаем вывод, что время всего полета тела вдвое больше времени его подъема до максимальной высоты, то есть получается, что время подъема тела до высоты H равно времени его падения на землю с этой максимальной высоты.
Модуль скорости v2 найдем из уравнения (2) для момента t = t2. Уравнение в этом случае примет вид: v2y = v0 – gt2.
Вспомним, что t2 = , тогда v2y = v0 – 2 v0 = – v0. По знаку проекции видим, что скорость v2 направлена в сторону, противоположную направлению оси Y, то есть вертикально вниз, что для нас очевидно из жизненного опыта. Модуль скорости находим как обычно, применяя формулу векторной алгебры
v2
=
 =
=
 = v0.
Таким образом, с какой по величине
скоростью тело было брошено вверх, с
такой же по величине скоростью оно упало
на землю.
= v0.
Таким образом, с какой по величине
скоростью тело было брошено вверх, с
такой же по величине скоростью оно упало
на землю.
Ответ: t1 = , H = , t2 = , v2 = v0.
Задача 8. Тело свободно падает с высоты h = 19,6 м. Какой путь S1 пройдет тело за первую t1 = 0,1 c своего движения? Какой путь S2 пройдет тело за последнюю t2 = 0,1 c своего движения?
Дано: h = 19,6 м, v0 = 0, t1 = 0,1 c, t2 = 0,1 c.
S1 − ? S2 − ?
Решение.
Записываем кинематическое уравнение движения с постоянным ускорением:
r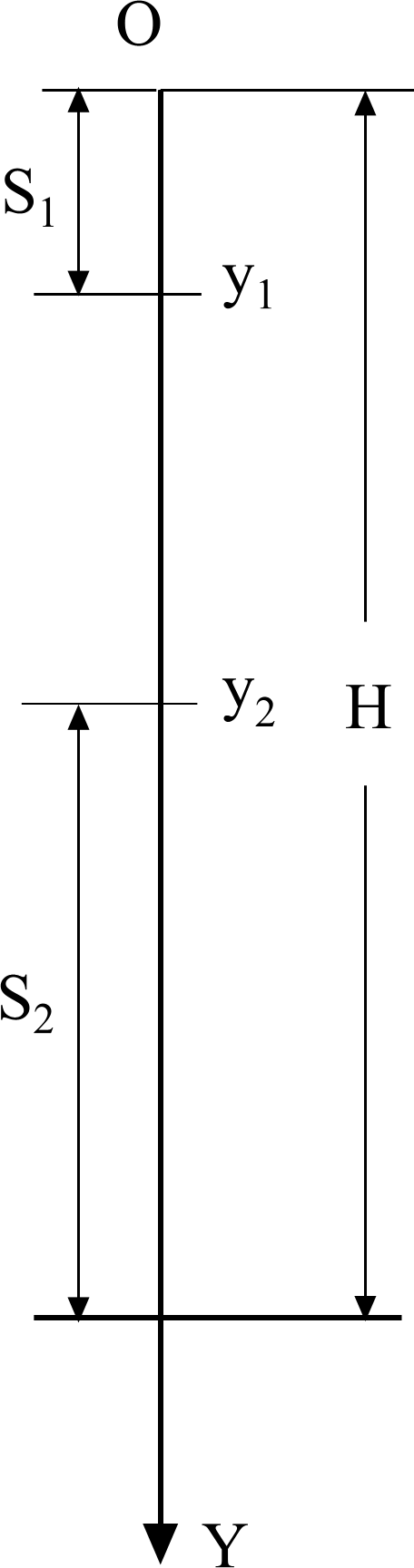 = r0
+ v0t
+
.
= r0
+ v0t
+
.
То же самое в проекциях на ось Y:
y = y0 + v0yt +.
Направление оси Y выбираем по вертикали вниз. Начало оси совмещаем с точкой начала движения (см. рисунок). За начало отсчета времени выбираем момент начала движения.
Находим проекции: y0 = 0, v0y = 0, gy = g.
Тогда
y = .
В момент времени t1 тело окажется в точке с координатой y1. Уравнение движения в этом случае примет вид: y1 = . Пройденный путь находим по формуле: S1 = y1 – 0 = y1.
S1 = . Подставив числовые значения, получим: S1 = 0,049 м.
Чтобы найти путь S2, пройденный телом за последнюю 0,1 с движения, надо, очевидно, из координаты тела, которую оно имеет при ударе о землю (а эта координата равна H) вычесть координату y2. Координату y2 можно найти из кинематического уравнения движения, но для этого надо знать время (обозначим его t′), за которое тело долетит из точки 0 до точки с координатой y2. А это время можно узнать, если из времени всего движения tпол вычесть последнюю 0,1 с движения, то есть t2.
Итак, находим полное время движения тела. Для этого опять воспользуемся уравнением движения и запишем его для момента удара тела о землю. Учтем при этом, что в этот момент координата тела будет H.
Тогда
H
=
 ,
откуда tпол
=
,
откуда tпол
=
 .
Подставив числа, получим: tпол
= 2 с. Находим t′:
t′
= tпол
– 0,1 = 1,9 с. Теперь находим y2:
y2
=
.
Подставив числа, получим: tпол
= 2 с. Находим t′:
t′
= tпол
– 0,1 = 1,9 с. Теперь находим y2:
y2
=
 .
Подставив числовые данные, получим:
y1
= 17,7 м. Тогда S2
= H
– y2.
S2
= (19,6 – 17,7) м = 1,9 м.
.
Подставив числовые данные, получим:
y1
= 17,7 м. Тогда S2
= H
– y2.
S2
= (19,6 – 17,7) м = 1,9 м.
Ответ: S1 = 0,049 м, S2 = 1,9 м.
Задача 9. Тело свободно падает с высоты h = 19,6 м. За какое время t1 тело пройдет первый S1 = 1 м своего пути? За какое время t2 тело пройдет последний S2 = 1 м своего пути?
Дано: h = 19,6 м, v0 = 0, S1 = 1 м, S2 = 1 м.
t1 − ? t2 − ?
Решение.
З аписываем
кинематическое уравнение движения с
постоянным ускорением:
аписываем
кинематическое уравнение движения с
постоянным ускорением:
r = r0 + v0t + .
То же самое в проекциях на ось Y:
y = y0 + v0yt + .
Направление оси Y выбираем по вертикали вниз. Начало оси совмещаем с точкой начала движения (см. рисунок). За начало отсчета времени выбираем момент начала движения.
Находим проекции: y0 = 0, v0y = 0, gy = g.
Тогда y = .
В момент времени t1 тело окажется в точке с координатой y1. Уравнение движения в этом случае примет вид: y1 = . Пройденный путь S1 = y1 – 0 = y1. Тогда
S1
=
,
откуда t1
=
 .
Подставляем числа и получаем: t1
= 0,45 с.
.
Подставляем числа и получаем: t1
= 0,45 с.
Чтобы найти время t2, за которое тело пройдет последний 1 м своего пути, надо, очевидно, из всего времени движения тела tпол вычесть время t′, за которое тело достигнет координаты y2, то есть t2 = tпол – t′.
Находим
полное время движения тела. Для этого
опять воспользуемся уравнением движения
и запишем его для момента удара тела о
землю. Учтем при этом, что в этот момент
координата тела будет H.
Тогда H
=
,
откуда
tпол
=
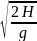 .
Подставив числа, получим: tпол
= 2 с.
.
Подставив числа, получим: tпол
= 2 с.
Время
t′
найдем из уравнения движения тела,
записанного для координаты y2.
Поскольку y2
=
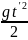 ,
то t′
=
,
то t′
=
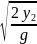 .
Координата y2
= Н – S2,
тогда t′
=
.
Координата y2
= Н – S2,
тогда t′
=
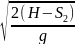 .
Подставив числа, получим: t′
= 1,95 с. Тогда t2
= tпол
– t′
= (2 – 1,95) с = 0,05 с.
.
Подставив числа, получим: t′
= 1,95 с. Тогда t2
= tпол
– t′
= (2 – 1,95) с = 0,05 с.
Ответ: t1 = 0,45 с, t2 = 0,05 с.
Задача 10. Свободно падающее тело в последнюю секунду движения проходит половину своего пути. С какой высоты h падает тело, и каково время t2 его падения?
Дано: h1 = h/2.
h − ? t2 − ?
Решение.
Записываем кинематическое уравнение движения с постоянным ускорением:
r = r0 + v0t + .
То же самое в проекциях на ось Y:
y = y0 + v0yt + .
Направление оси Y выбираем по вертикали вниз. Начало оси совмещаем с точкой начала движения (см. рисунок). За начало отсчета времени выбираем момент начала движения.
Н аходим
проекции: y0
= 0, v0y
= 0, gy
= g.
аходим
проекции: y0
= 0, v0y
= 0, gy
= g.
Тогда y = .
Запишем последнее уравнение для двух моментов времени: t1 и t2.
y1 = , y2 = .
Но
y1
=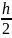 ,
y2
= h,
тогда
=
,
h
=
.
,
y2
= h,
тогда
=
,
h
=
.
Из
двух последних уравнений следует, что
2
=
или 2g
= g .
.
По условию задачи время достижения телом координаты y1 на 1 с меньше полного времени движения t2, то есть t1 = t2 – 1. Тогда 2g (t2 – 1)2 = g . Выполнив простые преобразования, получим: − 4t2 + 2 = 0. Решаем это уравнение и находим его корни: (t2)1 = 3,4 с, (t2)2 = 0,59 с.
Второй корень отбрасываем, поскольку он не соответствует условию задачи. Действительно, тело не может пролететь весь путь за 0,59 с, если оно за 1 с пролетает половину пути.
Высоту h найдем из уравнения движения, записанного для координаты y2 или, что то же самое, для момента времени t2: h = . Подставив числа, получим: h = 57 м.
Ответ: t2 = 3,4 с, h = 57 м.
Задача 11. Камень брошен вертикально вверх. На высоте h он побывал дважды с интервалом времени Δt. Определить величину v0 начальной скорости бросания камня.
Дано: h, Δt.
v0 − ?
Решение.
З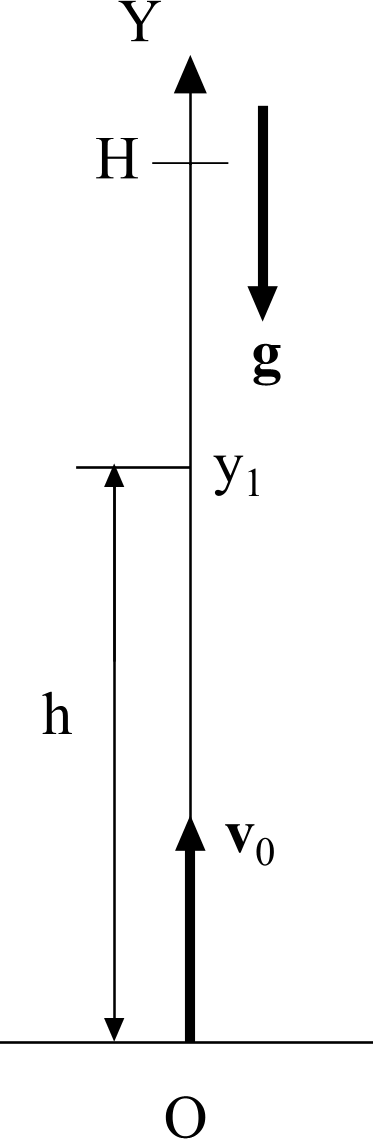 аписываем
кинематическое уравнение движения с
постоянным ускорением:
аписываем
кинематическое уравнение движения с
постоянным ускорением:
r = r0 + v0t + .
То же самое в проекциях на ось Y:
y = y0 + v0yt + .
Направление оси Y выбираем по вертикали вверх. Начало оси совмещаем с точкой начала движения (см. рисунок). За начало отсчета времени выбираем момент начала движения.
Находим проекции: y0 = 0, v0y = v0, gy = − g.
Тогда y = v0t − .
В точке с координатой y1 камень побывал в момент времени t1, когда поднимался вверх, и в момент t2, после того, как, поднявшись до максимальной высоты Н, стал падать обратно.
Запишем уравнение движения для этих двух моментов времени, учтя, что у1 = h, а t2 = t1 + Δt.
При подъеме: h = v0t1 – . (1)
При
падении: h
= v0
(t1
+ Δt)
–
 .
.
Поскольку левые части двух последних уравнений одинаковы, равны и их правые части:
v0
t1
–
= v0
(t1
+ Δt) –
.
Выполнив
элементарные преобразования, найдем:
t1
=
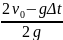 .
Подставим это выражение в уравнение
(1) и после простых действий получим:
v0
.
Подставим это выражение в уравнение
(1) и после простых действий получим:
v0 .
.
Ответ:
v0 .
.
Задача 12. Тело бросают вертикально вверх со скоростью, величина которой равна v0. Одновременно с предельной высоты, которой оно может достичь, бросают вертикально вниз другое тело с начальной скоростью V0, величина которой тоже равна v0. Определить время τ, по истечении которого тела встретятся и высоту h встречи.
Дано: v0 = V0.
τ − ? h − ?
Решение.
Записываем кинематические уравнения движения с постоянным ускорением для обоих тел:
r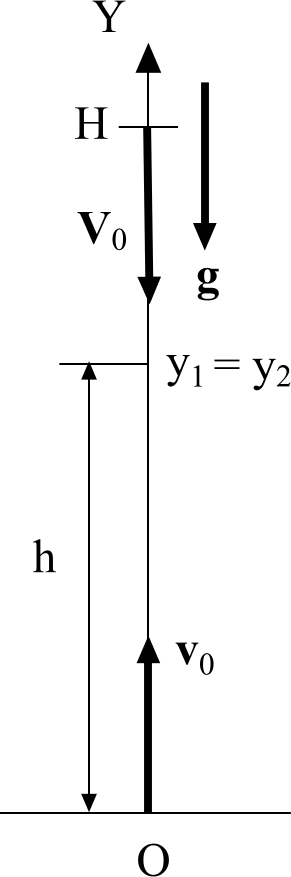 1
= r10
+ v0t
+
,
1
= r10
+ v0t
+
,
r2 = r20 + V0t + .
То же самое в проекциях на ось Y:
y1 = y10 + v0yt + ,
y2 = y20 + V0yt + .
Направление оси Y выбираем по вертикали вверх. Начало оси совмещаем с поверхностью земли (см. рисунок). За начало отсчета времени выбираем момент начала движения тел.
Находим проекции: y10 = 0, v0y = v0, gy = − g, y20 = H (в условии Н не задана, но ее легко найти), V0y = − V0 = − v0. Тогда
y1
= v0
t
–

y2 = H − v0 t − .
В момент t = τ тела встретились, и их координаты стали равны друг другу, то есть y1 = y2 = h. Тогда последние два уравнения примут вид:
h
= v0
τ
–
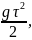 (1)
(1)
h
= H
− v0
τ
−
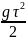 .
.
Максимальная высота H = (см. решение задачи 11.2.7).
Тогда последнее уравнение примет вид:
h = − v0 τ − (2)
Левые части уравнений (1) и (2) равны, следовательно, равны их правые части:
v0 τ – = − v0 τ − .
Отсюда легко находим время встречи.
τ
=
 .
.
Подставив последнее выражение в (1) или (2), найдем:
h
=
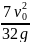 .
.
Ответ: τ = , h = .
Задача 13. Тело бросают с поверхности земли со скоростью, величина которой равна v0, под углом α к горизонту. Найти: 1) время t1 достижения максимальной высоты; 2) максимальную высоту Н, на которую поднимется тело; 3) время t2 движения тела от момента броска до момента падения на землю; 4) дальность L полета тела по горизонтали; 5) угол β, под которым нужно бросить тело, чтобы его дальность полета по горизонтали была максимальной; 6) величину v2 скорости, с которой тело упадет на землю; 7) угол γ падения тела на землю; 8) уравнение траектории тела.
Дано: v0, α.
t1 − ? Н − ? t2 − ? L − ? β − ? v2 − ? γ − ? y = φ(х) − ?
Решение.
Записываем кинематическое уравнение движения и уравнение скорости тела при движении с постоянным ускорением:
r = r0 + v0t + ,
v = v0 + gt.
Поскольку движение тела происходит в плоскости, то проектировать эти векторные уравнения следует на две оси.
Удобно выбрать две взаимно перпендикулярные оси, одна из которых (ось X) направлена по горизонтали, а другая (ось Y) – по вертикали. Начало данной системы координат совместим с точкой, откуда было брошено тело (см. рисунок). Время будем отсчитывать от момента броска.
С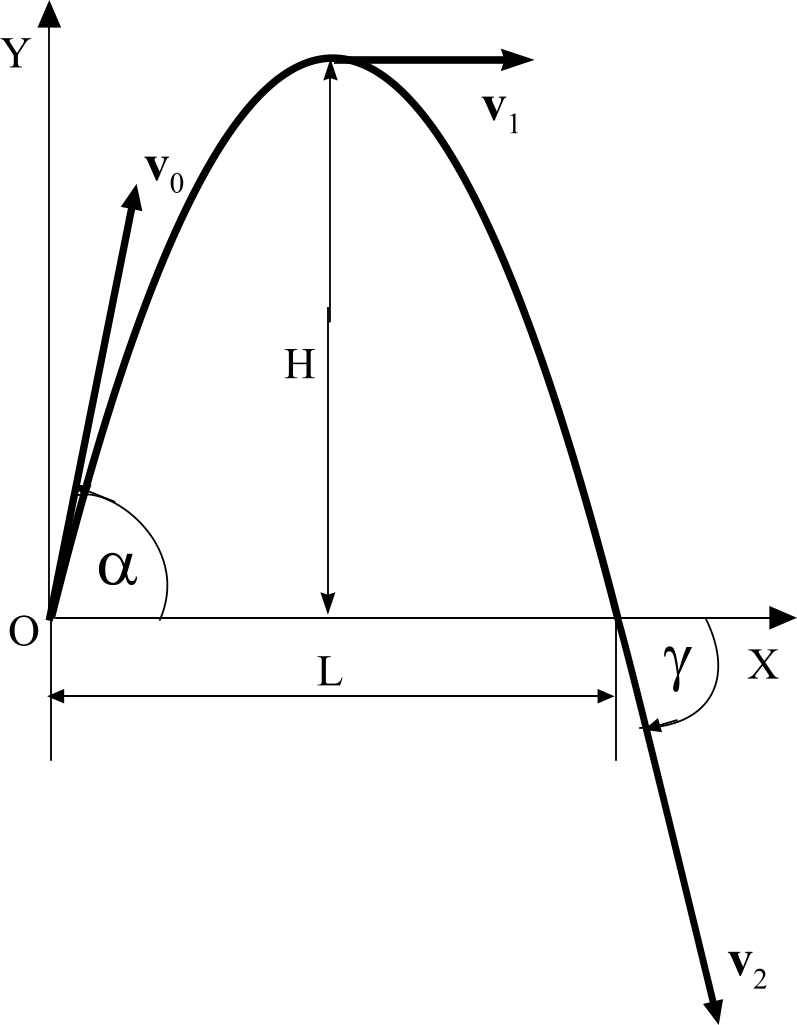 проектируем
записанные выше векторные уравнения
на выбранные оси:
проектируем
записанные выше векторные уравнения
на выбранные оси:
x
= x0
+ v0xt
+
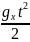 ,
,
y = y0 + v0yt + ,
vx = v0x + gxt,
vy = v0y + gyt.
Найдем проекции: x0 = 0, v0x = v0 Cos α,
gx = g Cos 900 = 0, y0 = 0,
v0y = v0 Cos (900 – α) = v0 Sin α,
gy = g Cos 1800 = – g.
С учетом найденных проекций имеем:
x = v0 (Cos α) t, (1)
y = v0 (Sin α) t – , (2)
vx = v0 Cos α, (3)
vy = v0 Sin α – gt. (4)
Следует иметь в виду, что кроме этих четырех уравнений мы более ни чем не располагаем, поэтому все ответы на вопросы задачи следует искать только в этих уравнениях.
Уравнение (1) не позволит нам получить ответ на первый вопрос задачи. Действительно, в момент времени t = t1 тело будет иметь координату x1, а мы ее не знаем. Поэтому получаем одно уравнение с двумя неизвестными.
Такая же ситуация возникает, если мы воспользуемся уравнением (2), поскольку в момент t = t1 неизвестна координата y1 (кстати, y1 = Н, то есть это – максимальная высота подъема, которую мы тоже должны найти).
В уравнение (3) время вообще не входит. Остается уравнение (4), и вот оно нам действительно поможет. В момент t = t1 вектор скорости v1 направлен горизонтально (смотри рисунок), и его проекция на вертикальную ось равна нулю, следовательно, уравнение (4) для данного момента времени будет выглядеть так:
0 = v0 Sin α – gt1, откуда
t1
= v0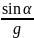 .
(5)
.
(5)
Ответ на второй вопрос даст нам уравнение (2). Для момента t1 данное уравнение примет вид:
Н = v0 (Sin α) t1 – .
Но t1 мы уже нашли, поэтому, подставив выражение для t1 из (5) в последнее уравнение, после простых преобразований получим:
Н
= .
.
Чтобы найти время t2, воспользуемся уравнением (2). В этот момент времени тело упало на землю, и его координата y2 стала равной нулю. Уравнение (2) принимает следующий вид:
0 = v0 (Sin α) t2 – . Отсюда легко находим искомое время.
t2
=
 .
(6)
.
(6)
Дальность полета тела по горизонтали найдем из уравнения (1). В момент t = t2 координата x = L, и уравнение принимает вид: L = v0 (Cos α) t2. Подставив сюда вместо t2 его выражение из (6), получим:
L
=
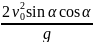 .
Но 2 Sin
α
Cos
α
= Sin
2α,
тогда
.
Но 2 Sin
α
Cos
α
= Sin
2α,
тогда
L
=
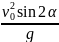 (7).
(7).
Проанализируем
это уравнение. Если v0
и g
постоянные величины (а для данной задачи
это так и есть), то дальность полета
будет зависеть только от угла бросания
тела. В зависимости от значения этого
угла синус будет принимать разные
значения, что и будет определять величину
L.
И тогда, когда синус будет максимален,
максимальна будет и дальность полета.
Но максимальное значение синуса равно
единице. Тогда Lmax
=
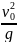 .
.
В свою очередь синус максимален, когда его аргумент равен 900, то есть 2α = 900, откуда α = 450. В условии задачи этот угол, при котором L = Lmax обозначен β. Таким образом, β = 450.
Величину
скорости v2,
с которой тело упадет на землю, легко
найти по известной формуле векторной
алгебры: v2
=
 .
Проекции скорости v2
на координатные оси найдем по формулам
(3) и (4).
.
Проекции скорости v2
на координатные оси найдем по формулам
(3) и (4).
v2x = v0 Cos α,
v2y = v0 Sin α – gt2.
Время
t2
мы уже нашли (формула 6). Тогда v2y
= v0
Sin
α
–
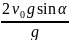 ,
,
v2y = – v0 Sin α. Подставив эти проекции в формулу для нахождения модуля v2, после простых преобразований, получим: v2 = v0.
Таким образом, с какой по величине скоростью тело было брошено, с такой же оно и упало на землю.
Угол
γ
найдем по его тангенсу. Из рисунка видно,
что tg
γ
=
 .
.
tg
γ = –
 =
– tg α.
=
– tg α.
Поскольку тангенс функция нечетная, то – tg α = tg (– α). Следовательно,
tg γ = tg (– α), откуда γ = – α, то есть по величине углы равны, но имеют разные знаки, что соответствует правилу определения знака угла в геометрии.
И, наконец, найдем уравнение траектории тела, то есть уравнение линии движения тела. А это – зависимость между его координатами.
Чтобы
найти эту зависимость, надо воспользоваться
уравнениями (1) и (2), исключив из них
время. Из (1) имеем: t
=
 .
.
Подставив это выражение в (2), получим:
y
=
 –
–
 ,
y = x tg α –
.
,
y = x tg α –
.
Введем
обозначения: tg
α
= b,
–
 = а. Тогда y
= аx2
+ bx.
= а. Тогда y
= аx2
+ bx.
Это – уравнение параболы, следовательно, траекторией движения тела является парабола. Поскольку а < 0, то ветви параболы направлены вниз.
Ответ: t1 = v0 , Н = , t2 = , L = , β = 450, v2 = v0,
γ = – α, траекторией тела является парабола.
Задача 14. Тело, брошенное со скоростью величиной v0 = 10 м/с под углом α = 450 к горизонту, ударяется о стенку ab, находящуюся на расстоянии L = 7 м от места бросания. Найти время t1 полета тела от момента бросания до удара о стенку. Найти величину скорости v1 тела в момент удара о стенку. Когда происходит удар тела о стенку, при его подъеме или при падении? Найти угол β, который составляет вектор скорости тела при ударе о стенку с положительным направлением оси X. На какой высоте h тело ударилось о стенку, считая от высоты, с которой оно брошено?
Дано: v0 = 10 м/с, α = 450, L = 7 м.
t1 − ? v1 − ? β − ? h − ?
Решение.
Эта задача похожа на предыдущую, только здесь телу не удалось продолжить свой полет по параболе из-за стенки (см. рисунок).
Т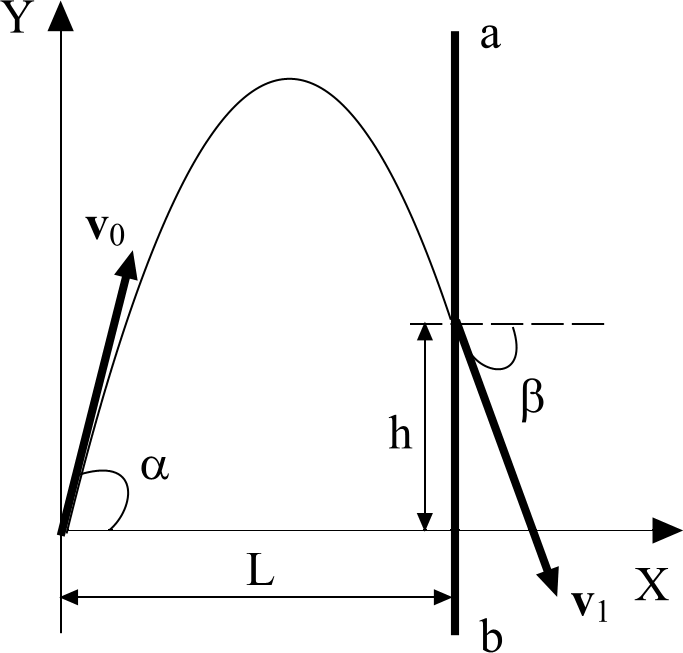 ем
не менее, движение тела также происходит
в поле тяготения с постоянным ускорением
g,
поэтому начало решения этой задачи
полностью соответствует началу решения
предыдущей. Итак, имеем четыре уравнения:
ем
не менее, движение тела также происходит
в поле тяготения с постоянным ускорением
g,
поэтому начало решения этой задачи
полностью соответствует началу решения
предыдущей. Итак, имеем четыре уравнения:
x = v0 (Cos α) t, (1)
y = v0 (Sinα) t – , (2)
vx = v0 Cos α, (3)
vy = v0 Sin α – gt. (4)
Ответ
на первый вопрос задачи даст нам уравнение
(1). Действительно, в момент удара о
стенку, то есть, когда t
= t1,
тело будет иметь координату L,
поэтому это уравнение примет вид: L
= v0
(Cos
α)
t1,
откуда t1
=
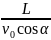 .
.
Подставив числовые значения входящих в формулу величин, получим: t1 = 1 с.
Величину
скорости тела при его ударе о стенку
найдем, зная проекции этой скорости на
координатные оси в момент удара по
известной формуле векторной алгебры:
v1
=
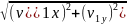 .
Сами же проекции вычислим, используя
формулы (3) и (4).
.
Сами же проекции вычислим, используя
формулы (3) и (4).
В
момент t
= t1
v1x
= v0
Cos
α
и v1y
= v0
Sin
α
– gt1.
Подставив числовые значения, получим:
v1x
= 7,1 м/с, v1y
= – 2,9 м/с. Тогда v1
=
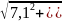 м/с = 7,7 м/с.
м/с = 7,7 м/с.
О том, когда произошел удар тела о стенку, при подъеме тела или при его падении, можно узнать по знаку проекции скорости v1 на ось Y. Если тело ударилось при подъеме, то угол между направлением скорости и направлением оси Y острый, и проекция будет положительной, а если удар произошел при падении, то угол будет тупой, и проекция в этом случае будет отрицательной. В нашем случае v1y < 0 (– 2,9 м/с), поэтому тело ударилось о стенку при падении, то есть после того, как оно пролетело верхнюю точку своей траектории. Угол β можно найти по его косинусу, используя формулу векторной алгебры:
v1x = v1 Cos β.
Cos
β =
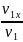 ,
Cos β =
,
Cos β =
 =
0,922. Отсюда
β
≈ 220.
Можно найти этот угол и по тангенсу (это
даже лучше): tg
β
=
=
0,922. Отсюда
β
≈ 220.
Можно найти этот угол и по тангенсу (это
даже лучше): tg
β
=
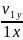 ,
tgβ
= –
,
tgβ
= –
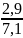 =
– 0,408. Этому значению тангенса соответствует
тот же угол, только со знаком минус: β
≈ – 220.
Откуда этот минус взялся, и почему при
нахождении угла по косинусу его не было?
Дело в том, что косинус – функция четная,
то есть косинусы одинаковых по величине
но разных по знаку углов, одинаковы. А
знак угла говорит о том по ходу часовой
стрелки или против повернут вектор
относительно оси. Поэтому, вычислив по
косинусу величину угла, на который
повернут вектор относительно оси, мы
не можем сказать, в какую сторону он
повернут. Другое дело, если мы находим
угол по тангенсу. Тангенс (как и синус)
– функция нечетная, то есть положительному
углу соответствует положительный
тангенс, а отрицательному – отрицательный.
В результате решения у нас получился
отрицательный тангенс, следовательно,
и угол β
тоже должен быть отрицательным. И теперь
уже мы не ошибемся с направлением
вектора: отрицательные углы отсчитываются
относительно оси по ходу часовой стрелки
(положительные – против хода). Конечно,
в нашей задаче итак видно, куда направлен
вектор скорости v1,
но ведь могут встретиться задачи, где
направление вектора неочевидно. Поэтому
на будущее советую определять направление
вектора по нечетной функции, тангенсу
или синусу.
=
– 0,408. Этому значению тангенса соответствует
тот же угол, только со знаком минус: β
≈ – 220.
Откуда этот минус взялся, и почему при
нахождении угла по косинусу его не было?
Дело в том, что косинус – функция четная,
то есть косинусы одинаковых по величине
но разных по знаку углов, одинаковы. А
знак угла говорит о том по ходу часовой
стрелки или против повернут вектор
относительно оси. Поэтому, вычислив по
косинусу величину угла, на который
повернут вектор относительно оси, мы
не можем сказать, в какую сторону он
повернут. Другое дело, если мы находим
угол по тангенсу. Тангенс (как и синус)
– функция нечетная, то есть положительному
углу соответствует положительный
тангенс, а отрицательному – отрицательный.
В результате решения у нас получился
отрицательный тангенс, следовательно,
и угол β
тоже должен быть отрицательным. И теперь
уже мы не ошибемся с направлением
вектора: отрицательные углы отсчитываются
относительно оси по ходу часовой стрелки
(положительные – против хода). Конечно,
в нашей задаче итак видно, куда направлен
вектор скорости v1,
но ведь могут встретиться задачи, где
направление вектора неочевидно. Поэтому
на будущее советую определять направление
вектора по нечетной функции, тангенсу
или синусу.
И, наконец, осталось ответить на последний вопрос задачи. Для этого используем уравнение (2). В момент удара, когда t = t1, координата тела по оси Y равна h. Тогда уравнение (2) запишется так: h = v0 (Sin α) t1 – . После подстановки числовых значений, получим: h = 2,1 м.
Ответ: t1 = 1 с, v1 = 7,7 м/с, удар происходит при падении тела, β ≈ – 220,
h = 2,1 м.
Задача 15. Шарик свободно падает с высоты h на наклонную плоскость, которая составляет угол α с горизонтом. Найти расстояния s1, s2, s3, и т.д. между точками, в которых подпрыгивающий шарик касается наклонной плоскости. Соударения шарика с наклонной плоскостью считать абсолютно упругими.
Дано: h, α.
s1, s2, s3… − ?
Решение.
Вначале найдем скорость, с которой шарик упадет на наклонную плоскость. Обозначим скорость падения шарика как u. Шарик движется с постоянным ускорением g, поэтому его уравнение движения и уравнение скорости будут выглядеть так (запишем их сразу в проекциях на ось Y):
y = y0 + u0yt + , uy = u0y + gyt.
Направим ось вертикально вниз, а ее начало совместим с точкой, откуда шарик начал свое движение (см. рисунок). Отсчет времени будем вести с момента начала движения шарика.
П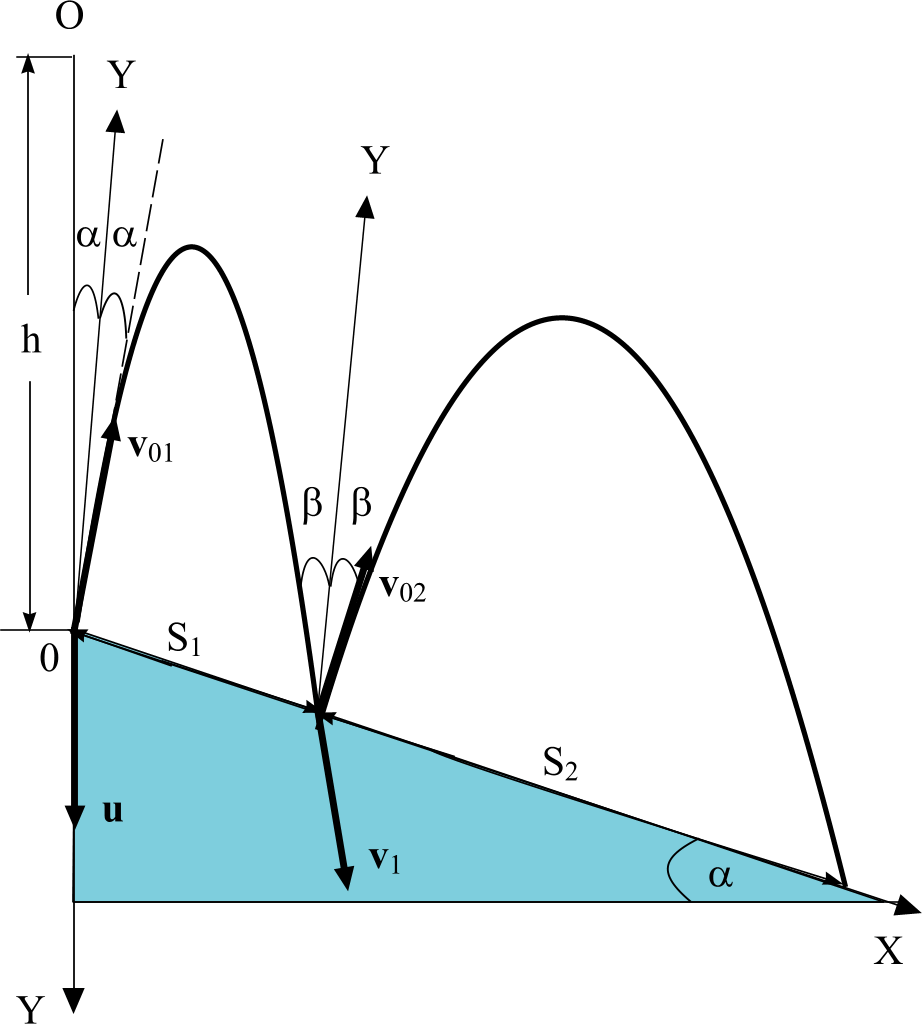 оскольку
начальная скорость шарика u0
равна нулю (поэтому его падение и называют
свободным), и начальная координата y0
= 0, то предыдущие уравнения примут вид:
оскольку
начальная скорость шарика u0
равна нулю (поэтому его падение и называют
свободным), и начальная координата y0
= 0, то предыдущие уравнения примут вид:
y = , uy = gyt.
Учитывая, что gy = g, uy = u, запишем эти уравнения для момента t = t1, когда шарик коснулся плоскости (в этот момент его координата равна h, а величина скорости равна u1): h = , u1 = gt1.
Из
предпоследнего уравнения находим t1:
t1
=
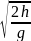 .
Подставив это выражение в последнее
уравнение, найдем искомую скорость: u1
=
.
Подставив это выражение в последнее
уравнение, найдем искомую скорость: u1
=
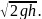
После касания плоскости, шарик от нее отразится (отскочит) с какой-то скоростью. Обозначим ее v01.
Известно, что при абсолютно упругом соударении с плоскостью шарик при отскоке будет иметь такую же по величине скорость, что и при ударе, то есть
u1 = v01.
Таким образом, v01 = Кроме того, угол падения шарика равен углу его отскока. При этом надо иметь в виду, что угол падения – это угол между линией, вдоль которой направлена скорость падения u и перпендикуляром к плоскости в точке удара (из рисунка видно, что это – угол α), а угол отражения – это угол между направлением скорости отскока v01 и тем же перпендикуляром. Дальнейшее движение шарика будет происходить по параболе (точнее, по части параболы), что видно из решения предыдущей задачи.
Анализ движения шарика после первого удара о плоскость проведем в системе координат, показанной на рисунке, то есть ось X направим вдоль наклонной плоскости, а ось Y – перпендикулярно ей. Обычно, когда решаются задачи с наклонной плоскостью, именно так выбирают направления координатных осей, в этом случае решение задач несколько (а иногда и существенно) упрощается. Начало этой системы координат совместим с точкой второго удара шарика о плоскость. Отсчет времени будем вести с момента второго отскока.
Запишем уравнение движения тела и уравнение для его скорости при движении с постоянным ускорением (в данном случае с ускорением свободного падения g) для момента t = t1, когда шарик во второй раз падает на плоскость.
Запишем сразу эти уравнения в проекциях на координатные оси. При этом учтем, что начальные координаты шарика в выбранной системе координат равны нулю.
x1
= v01xt1
+
 ,
,
y1
= v01yt1
+
 ,
,
v1x = v01x + gxt1,
v1y = v01y + gyt1.
Находим проекции:
v01x = v01 Cos (900 – α) = v01 Sin α, gx = g Cos (900 – α) = g Sin α, v01y = v01 Cos α,
gy = g Cos (1800 – α) = – g Cos α. С учетом найденных проекций предыдущие четыре уравнения примут вид:
x1
= v01
(Sin
α) t1
+ g (Sin α)
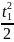 ,
(1)
,
(1)
y1 = v01 (Cos α) t1 – g (Cos α) , (2)
v1x = v01 Sin α + g (Sin α) t1, (3)
v1y = v01 Cos α – g (Cos α) t1. (4)
Найдем время t1 полета шарика между первым и вторым ударами о плоскость. Это нам поможет сделать уравнение (2). В момент второго удара ордината y1 шарика равна нулю. Тогда данное уравнение запишется так:
0
= v01
(Cosα)
t1
– g
(Cos
α)
,
откуда t1
=
 .
.
В
этот же момент времени абсцисса шарика
будет равна s1,
и уравнение (1) примет вид: s1
= v01
(Sin
α)
t1
+ g
(Sin
α)
.
Подставив сюда найденное выражение для
t1,
после простых преобразований получим:
s1
=
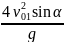 .
Так как v01
=
.
Так как v01
=
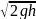 ,
то окончательно имеем: s1
= 8h
Sin
α.
,
то окончательно имеем: s1
= 8h
Sin
α.
Подставим выражение для t1 в уравнения (3) и (4). Получим:
v1x = v01 Sin α + g (Sin α) или v1x = 3v01 Sin α.
v1y = v01 Cos α – g (Cos α) или v1y = – v01 Cos α. Эти выражения для проекций скоростей нам вскоре пригодятся.
Перейдем к нахождению расстояния вдоль наклонной плоскости между вторым и третьим соударениями. Систему координат оставим прежней, только ее начало перенесем в точку второго соударения шара с плоскостью. Время будем отсчитывать от момента второго соударения.
Шар падает на плоскость в данной точке со скоростью v1 под углом β и отскакивает под тем же по величине углом со скоростью v02, причем β ≠ α, а
v02 = v1. Запишем кинематическое уравнение движение шара в этом случае (сразу в проекциях на координатные оси):
x = v02xt + , (5)
y = v02yt + . (6)
Что можно сказать о v02x? Если внимательно посмотреть на рисунок, то видно, что скорости v1 и v02 составляют с осью X одинаковые по величине углы. Учитывая, что модули скоростей одинаковы, делаем вывод, что проекции этих скоростей на ось X равны между собой, то есть v02x = v1x. Но v1x мы недавно находили, тогда v02x = 3v01 Sin α.
Теперь о v02y. Эта проекция равна по величине v1y, только знак у нее будет противоположный. Действительно, вектор v02 составляет с осью Y угол β, а вектор v1 с этой же осью – угол 1800 – β. Поскольку Cos β = – Cos (1800 – β), то v02y = – v1y. Таким образом, v02y = v01 Cos α.
Вновь запишем уравнения (5) и (6), но уже для конкретного времени t2, когда шарик в третий раз падает на плоскость. При этом учтем полученные выражения для v02x, v02y, gx и gy.
Учтем также, что в этот момент времени абсцисса шарика будет равна s2, а ордината нулю.
s2
= 3v01
(Sin
α) t2
+ g (Sin α)
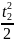 ,
,
0 = v01 (Cos α) t2 – g (Cos α) .
Из последнего уравнения находим t2: t2 = . Мы получили то же выражение, что и для t1, то есть время полета шарика между соударениями с плоскостью одно и то же. Теперь найдем s2:
s2
= 3v01
(Sin
α)
+ g (Sin α)
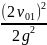 .
.
После простых преобразований, получим:
s2
=
 .
.
Ранее мы нашли, что v01 = . Тогда s2 = 16g Sin α.
Аналогично можно показать, что расстояние между третьим и четвертым соударениями s3 = 24g Sin α.
Ответ: s1 = 8h Sin α, s2 = 16h Sin α, s3 = 24h Sin α и т.д.
Вращательное движение.Решение задач
Задача 1. Сплошной диск катится без скольжения по горизонтальной плоскости с постоянной скоростью поступательного движения vп. Доказать, что величина линейной скорости vл вращения любой точки обода диска относительно центра О равна величине скорости его поступательного движения.
Решение.
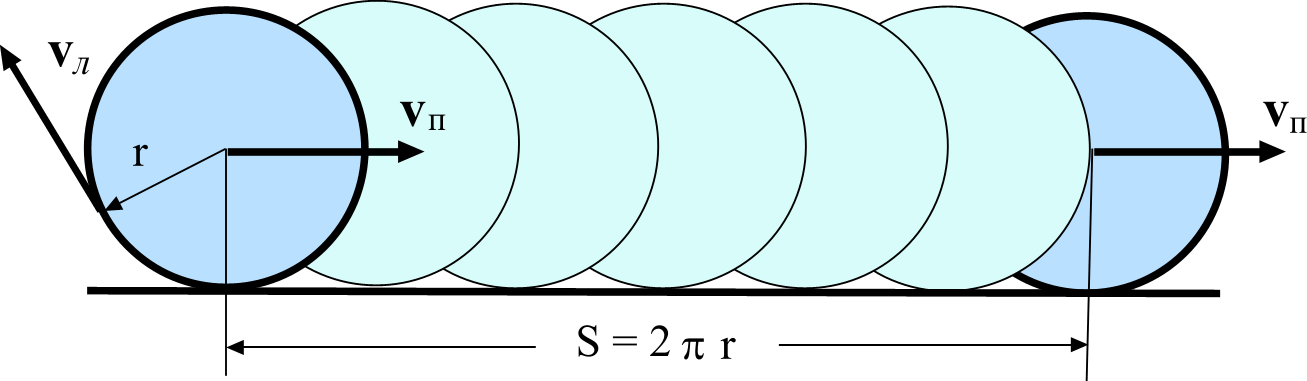
За время T полного оборота диск как целое пройдет путь S = vпT.
В то же время, этот путь равен длине окружности диска, то есть
S
= 2πr,
где r
– радиус диска (см. рисунок). Тогда vпT
= 2πr,
откуда vп
=
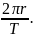
С
другой стороны, линейная скорость
вращения относительно центра О всех
точек диска, лежащих на его ободе, равна
vл
= ωr,
где ω
– угловая скорость вращения. Но ω
=
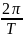 ,
следовательно, vл
=
,
следовательно, vл
=
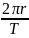 .
.
Таким образом, vл = vп.
Задача 2. Найти величину угловой скорости ω и величину линейной скорости v искусственного спутника Земли, если известно, что он вращается по круговой орбите с периодом обращения Т = 88 мин, и его орбита расположена на расстоянии h = 200 км от поверхности Земли.
Дано: Т = 88 мин = 5280 с, h = 200 км = 2∙105 м.
ω − ? v − ?
Решение.
Величину
угловой скорости найдем по формуле: ω
=
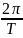 .
Подставив числовые значения, получим
ω
= 1,2∙10−3
с−1.
.
Подставив числовые значения, получим
ω
= 1,2∙10−3
с−1.
Величину линейной скорости найдем по формуле: v = ωR, где R – расстояние от центра Земли до траектории спутника, то есть радиус его орбиты. В свою очередь, R = RЗ + h. Здесь RЗ – это радиус Земли (он равен приблизительно 6,38∙106 м). Тогда v = ω(RЗ + h).
Подставив числа, получим: v = 7,8∙103 м/с.
Ответ: v = 7,8∙103 м/с, ω = 1,2∙10−3 с−1.
Задача 3. Найти величину линейной скорости v точек земной поверхности на широте Тулы (город находится на широте φ = 54,20).
Дано: φ = 54,20.
v − ?
Решение.
Величину линейной скорости найдем по формуле: v = ωr, где r – радиус окружности сечения земной сферы плоскостью, проходящей перпендикулярно к оси вращения Земли через точки с шириной 54,20. Поскольку ω = , r = RЗ Cos φ (см. рисунок), то v = RЗ Cos φ.

Здесь, Т – время одного полного оборота Земли вокруг своей оси
(Т = 24 час = 8,64∙104 с), RЗ – радиус Земли (он равен приблизительно 6,38∙106 м), Cos 54,20 = 0,585.
Подставив числа, получим: v = 271 м/с.
Ответ: v = 271 м/с.
Задача 4. Ось с двумя дисками, расположенными на расстоянии L = 0,5 м друг от друга, вращается с частотой n =30 оборотов в секунду. Пуля, летящая вдоль оси, пробивает оба диска; при этом отверстие от пули во втором диске смещено относительно отверстия в первом диске на угол φ1 = 120. Найти величину v скорости пули.
Дано: L = 0,5 м, n = 30 с–1, φ1 = 120 = 0,21 рад.
v − ?
Решение.
Найдем
время t1
пролета пули между дисками. t1
=
 .
За это же время диски успевают сместиться
на угол φ1
= ωt1.
Из последнего выражения найдем t1:
t1
=
.
За это же время диски успевают сместиться
на угол φ1
= ωt1.
Из последнего выражения найдем t1:
t1
=
 .
Тогда
=
,
откуда v
=
.
Тогда
=
,
откуда v
=
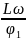 .
Поскольку ω
= 2πn,
то v
=
.
Поскольку ω
= 2πn,
то v
=
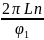 .
Подставив числа, получим:
.
Подставив числа, получим:
v = 448,6 м/с.
Ответ: v = 448,6 м/с.
Задача 5. Найти радиус R вращающегося колеса, если известно, что величина v1 линейной скорости точки, лежащей на ободе, в 2,5 раза больше величины v2 линейной скорости точки, лежащей на расстоянии r = 5 см ближе к оси колеса.
Дано: v1 = 2,5v2, r = 5 см = 5∙10−2 м.
R − ?
Решение.
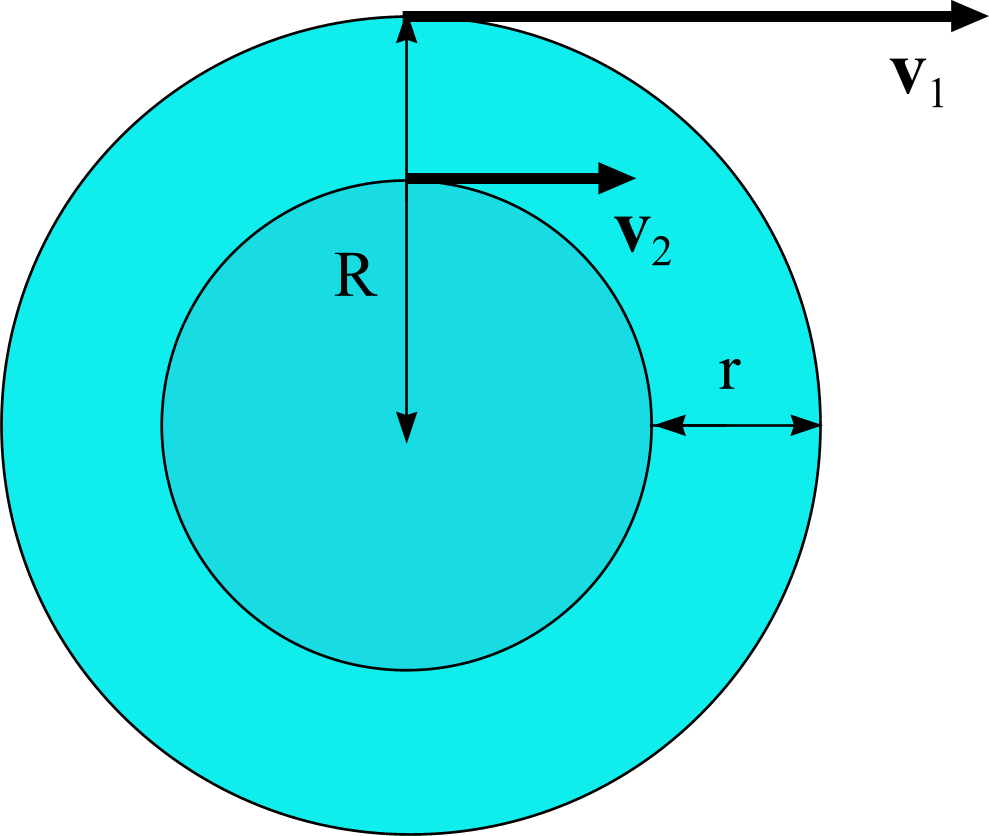
Поскольку
угловые скорости ω
всех точек колеса одинаковы, то величины
линейных скоростей указанных в условии
точек будут определяться выражениями:
v1
= ωR,
v2
= ω
(R
– r).
Тогда ωR
= 2,5ω
(R
– r),
откуда после простых преобразований
находим: R
=
 .
Подставив числа, получим:
.
Подставив числа, получим:
R = 8,3∙10−2 м = 8,3 см.
Ответ: R = 8,3 см.
Задача 6. Величина линейной скорости точек окружности вращающегося диска равна v1 = 3 м/с, а точек, находящихся на расстоянии r = 10 см ближе к оси вращения, v2 = 2 м/с. Какова частота n вращения диска?
Дано: v1 = 3 м/с, v2 = 2 м/с, r = 10 см = 10−1 м.
n − ?
Решение.
Поскольку угловые скорости ω всех точек диска одинаковы, то величины линейных скоростей указанных в условии точек будут определяться выражениями:
v1 = ωR, (1)
v2 = ω (R – r). (2)
Поделим
первое уравнение на второе:
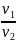 =
=
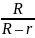 .
После простых преобразований
.
После простых преобразований
найдем
R:
R
=
 .
Подставив последнее выражение в (1),
найдем угловую
.
Подставив последнее выражение в (1),
найдем угловую
скорость:
ω
=
 .
Но ω
= 2πn.
Тогда 2πn
=
,
откуда n
=
.
Но ω
= 2πn.
Тогда 2πn
=
,
откуда n
=
 .
Подставив числа, получим:
.
Подставив числа, получим:
n = 1,6 с−1. Ответ: n = 1,6 с−1.
Задача 7. Диск, вращаясь равноускоренно, достиг величины угловой скорости ω1 = 20 с−1 через N1 = 10 оборотов после начала вращения. Найти величину ε углового ускорения диска, а также модули линейной скорости, нормального, касательного и полного ускорений точки диска, лежащей на расстоянии r = 1 м от оси вращения в этот момент времени.
Дано: ω1 = 20 с−1, N1 = 10, r = 1 м.
ε − ? v1 − ? | an1 | − ? | aτ1 | − ? a1 − ?
Решение.
Запишем кинематическое уравнение движения и уравнение для угловой скорости точки в полярных координатах при равноускоренном вращении. В этом случае векторы угловой скорости и углового ускорения совпадают по направлению. Ось Z направим в ту же сторону, куда направлены векторы ω и ε. Тогда проекции этих векторов будут равны их модулям, и интересующие нас уравнения будут выглядеть так:
φ
= ω0t
+
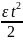 ,
,
ω = ω0 + εt.
Эти уравнения справедливы для любой точки диска. Рассмотрим какую-нибудь точку диска, лежащую на расстоянии r от оси вращения. В момент t = t1, когда диск (а, значит, и рассматриваемая точка) приобрел угловую скорость величиной ω1, уравнения примут вид:
φ1
= ω0t1
+
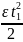 ,
(1)
,
(1)
ω1 = εt1. (2)
Выразим
t1
из (2) и подставим в (1), учтя при этом, что
φ1
= 2πN1.
После простых преобразований получим:2πN1
=
 ,
откуда ε
=
,
откуда ε
=
 .
Подставив числовые значения входящих
в формулу величин, будем иметь: ε
= 3,2 с−2.
.
Подставив числовые значения входящих
в формулу величин, будем иметь: ε
= 3,2 с−2.
Величину скорости v1 найдем по формуле: v1 = ω1r. Подставив числа, получим:
v1 = 2 м/с. Модули ускорений в момент t = t1найдем по следующим формулам:
|
an1
|
=
 ,
| aτ1
|
= εr, a =
,
| aτ1
|
= εr, a =
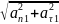 .
С
учетом числовых значений будем иметь:
.
С
учетом числовых значений будем иметь:
| an1 | = 4 м/с2, | aτ1 | = 3,2 м/с2, a = 5,1 м/с2.
Ответ: ε = 3,2 с−2, v1 = 2 м/с, | an1 | = 4 м/с2, | aτ1 | = 3,2 м/с2, a = 5,1 м/с2.
Задача 8. Диск, вращаясь равнозамедленно, за время t1 = 60 с уменьшил частоту своего вращения с n0 = 5 c−1 до n1 = 3 c−1, продолжая вращаться в ту же сторону. Найти величину ε углового ускорения диска и число оборотов N1 диска за это время.
Дано: t1 = 60 с, n0 = 5 c−1, n1 = 3 c−1.
ε − ? N1 − ?
Решение.
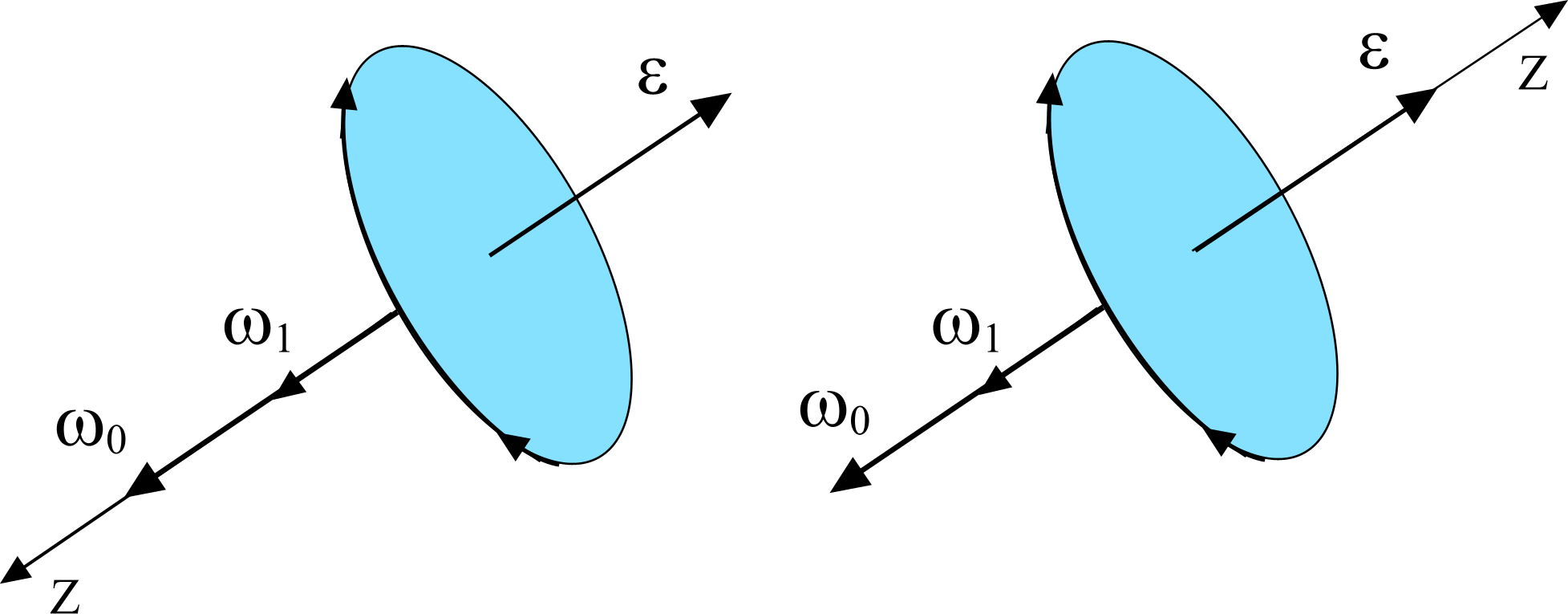
Запишем кинематическое уравнение движения и уравнение для угловой скорости какой-либо точки диска в полярных координатах при вращении с постоянным ускорением:
φ
= ω0zt
+
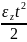 ,
,
ωz = ω0z + εzt.
В случае равнозамедленного вращения векторы угловой скорости и углового ускорения направлены в противоположные стороны. Найдем проекции. Вначале ось Z направим в сторону вектора начальной угловой скорости ω0 (рисунок слева). Затем решим эту же задачу, изменив направление оси на противоположное (рисунок справа). Итак, ω0z = ω0, εz = − ε, ωz = ω, и интересующие нас уравнения будут выглядеть так:
φ = ω0t − , (а)
ω = ω0 − εt. (b)
За начальное время выберем момент, когда диск имеет частоту вращения
n0 = 5 c−1.
Для момента t = t1, когда диск (а, значит, и рассматриваемая точка) приобрел угловую скорость ω1, уравнения будут выглядеть так:
φ1 = ω0t1 − ,
ω1 = ω0 − εt1.
Учтем, что φ1 = 2πN1, ω0 = 2πn0, а ω1 = 2πn1. Тогда уравнения примут вид:
2πN1 = 2πn0t1 − , (1)
2πn1 = 2πn0 − εt1. (2)
Из уравнения (2) найдем величину углового ускорения:
ε
=
 .
Подставив это выражение в (1), после
несложных преобразований найдем N1:
.
Подставив это выражение в (1), после
несложных преобразований найдем N1:
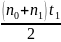 .
С учетом числовых значений ε
= 0,21 с−2,
N1
= 240.
.
С учетом числовых значений ε
= 0,21 с−2,
N1
= 240.
Теперь решим задачу, изменив направление оси Z на противоположное (рисунок справа).
В этом случае ω0z = − ω0, εz = ε, ωz = − ω. Кроме того, перед углом φ надо поставить знак минус. Почему? Дело в том, что φ – это угловая координата, которая принимает положительные значения, если угол отсчитывается от оси в направлении, противоположном ходу часовой стрелки (как на рисунке слева) и – отрицательные, если угол отсчитывается по ходу часовой стрелки (как на рисунке справа). Направления отсчета углов хорошо видны, если смотреть на диск с конца оси Z. Тогда
− φ = − ω0t + ,
− ω = − ω0 + εt.
Умножив левые и правые части уравнений на минус единицу, получим:
φ = ω0t − ,
ω = ω0 − εt.
Таким образом, мы получили те же уравнения (a) и (b), что и определяет такой же конечный результат решения, что и с предыдущим направлением оси. Так и должно быть: субъективный выбор оси не влияет на объективные процессы, происходящие в природе.
Ответ: ε = 0,21 с−2, N1 = 240 оборотов.
Задача 9. Диск, вращаясь равнозамедленно, за время t1 = 60 с уменьшил частоту своего вращения с n0 = 5 c−1 до n1 = 3 c−1, продолжая вращаться в ту же сторону. Найти величину ε углового ускорения диска и число оборотов N2 диска за время t2 = 5 мин.
Дано: t1 = 60 с, n0 = 5 c−1, n1 = 3 c−1, t2 = 5 мин = 300 с.
N2 − ?
Решение.
Эта
задача очень похожа на предыдущую.
Однако при решении следует проявить
осторожность. На первый взгляд может
показаться, что все очень просто: вначале
также находим величину углового
ускорения, а затем, используя для времени
t2
кинематическое уравнение движения
(2πN2
= 2πn0t2
–
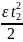 ),
найдем число оборотов N2
диска.
),
найдем число оборотов N2
диска.
Однако найденное по этой формуле значение N2 может оказаться не верным. Почему? Формула-то вроде правильная… Дело в том, что вполне может случиться так, что за промежуток времени от начала изучения движения (когда диск имел частоту n0) до момента t2 диск мог остановиться (вращение-то замедленное!), а потом начать вращаться в противоположном направлении с тем же по величине и направлению угловым ускорением.
При этом направление угловой скорости изменится на противоположное, оно станет совпадать с направлением углового ускорения, и вращение станет равноускоренным (см. рисунок).
« Ну
и что, формула-то все равно должна
работать, ведь она же для движения с
постоянным ускорением, а оно не меняется!»
− возможно, воскликнете Вы. Так, да не
совсем. Согласитесь, что при некотором
значении t2
правая часть формулы может принять
нулевое значение. Тогда получается, что
N2
равно нулю.
Ну
и что, формула-то все равно должна
работать, ведь она же для движения с
постоянным ускорением, а оно не меняется!»
− возможно, воскликнете Вы. Так, да не
совсем. Согласитесь, что при некотором
значении t2
правая часть формулы может принять
нулевое значение. Тогда получается, что
N2
равно нулю.
Как же так? Диск крутился, крутился в течение времени t2 и ничего не накрутил? Ни одного оборота? А ведь при некотором значении t2 правая часть формулы вообще может оказаться отрицательной, а уж отрицательными обороты (как и путь) быть никак не могут. Почему же так получается? Дело в том, что кинематическое уравнение справедливо для координаты (при вращении угол φ и есть угловая координата), поэтому, если бы в левой части формулы стоял угол φ2 (а не 2πN2), то уравнение «работало» бы, как говорится для всех времен и народов. Этот угол может быть равен и нулю, когда радиус-вектор точки совпадает с полярной осью, может быть и положительным и отрицательным, в зависимости от того, смещен ли радиус-вектор относительно полярной оси против хода часовой стрелки или по ходу. Выражать этот угол через количество оборотов можно, если вращение происходит в одну сторону.
Поэтому в нашем случае, сначала надо использовать формулу для подсчета числа оборотов, сделанных диском при равнозамедленном вращении до остановки, затем рассчитать количество оборотов, сделанных диском от момента остановки до момента t2 (а это уже будет равноускоренной вращение) и сложить эти числа.
Но вначале выясним, остановится ли диск и изменит ли он направление вращения в течение пяти минут? Мы имеем два уравнения, справедливых для любого момента времени:
φ = ω0t − , (1)
ωz = ω0 − εt. (2)
В
момент остановки (t
= tост.)
левая часть последнего уравнения
становится равной нулю. Тогда tост.
=
 =
=
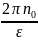 .
Величину углового ускорения мы уже
нашли в решении предыдущей задачи, не
будем повторяться (ε
= 0,21 с−2).
Подставив числа, получим: tост.
= 149,5 с. Итак, получается, что диск
практически половину времени вращался
замедленно, затем остановился, после
чего его вращение стало равноускоренным.
Найдем, сколько оборотов N′
сделал диск до остановки. Для этого
используем уравнение движения, записанного
для момента tост.:
.
Величину углового ускорения мы уже
нашли в решении предыдущей задачи, не
будем повторяться (ε
= 0,21 с−2).
Подставив числа, получим: tост.
= 149,5 с. Итак, получается, что диск
практически половину времени вращался
замедленно, затем остановился, после
чего его вращение стало равноускоренным.
Найдем, сколько оборотов N′
сделал диск до остановки. Для этого
используем уравнение движения, записанного
для момента tост.:
2πN′
= 2πn0tост.
−
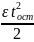 ,
откуда N′
=
,
откуда N′
=
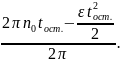 Подставив
числа, получим: N′
= 373,7.
Подставив
числа, получим: N′
= 373,7.
Теперь узнаем, сколько оборотов N′′ сделал диск, вращаясь равноускоренно.
Для этого вначале узнаем промежуток времени этого равноускоренного вращения. Обозначим его как Δt2.
Очевидно, Δt2 = t2 − tост. Δt2 = (300 – 149,5) с = 150,5 с. Теперь осталось воспользоваться уравнением (1) для вычисления N′′.
При
этом надо учесть, что начальная угловая
скорость равноускоренного вращения
равна нулю (это вращение началось с
момента остановки), а левая часть
уравнения будет равна − 2πN′′
(именно со знаком минус, поскольку угол
отсчитывается по ходу часовой стрелки,
об этом речь шла в предыдущей задаче).
Тогда − 2πN′′
= −
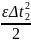 или
2πN′′
=
,
откуда N′′
=
или
2πN′′
=
,
откуда N′′
=
 .
Подставив числа, получим: N′′
= 189,3. Теперь найдем общее число оборотов
диска с момента начала наблюдения до
момента t2.
.
Подставив числа, получим: N′′
= 189,3. Теперь найдем общее число оборотов
диска с момента начала наблюдения до
момента t2.
N2 = N′ + N′′. Сложив числа, получим: N2 = 563.
Ответ: N2 = 563 оборота.
Задача 10. Точка движется равноускоренно по окружности радиусом R = 0,1 м с постоянным тангенциальным ускорением аτ. Найти величину нормального ускорения | а1n | точки через время t1 = 20 с после начала движения, если известно, что к концу пятого оборота после начала движения величина линейной скорости точки v5 = 0,1 м/с.
Дано: R = 0,1 м, t1 = 20 с, N5 = 5, v5 = 0,1 м/с.
| а1n | − ?
Решение.
В
момент t
= t1
модуль нормального ускорения | а1n
|
=
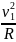 .
Так как v1
= ω1R,
то
.
Так как v1
= ω1R,
то
|
а1n
|
=
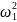 R.
Поскольку векторы угловой скорости и
углового ускорения при равноускоренном
вращении совпадают, и начальная угловая
скорость равна нулю, то ω1
= εt1.
Тогда
R.
Поскольку векторы угловой скорости и
углового ускорения при равноускоренном
вращении совпадают, и начальная угловая
скорость равна нулю, то ω1
= εt1.
Тогда
| а1n | = ε2 R. (1)
Для
нахождения величины углового ускорения
воспользуемся уравнением движения и
уравнением угловой скорости для
равноускоренного вращательного движения.
Эти уравнения запишем для момента t
= t5,
то есть, когда точка сделала пять полных
оборотов:φ5
=
 ,
ω5
= εt5.
,
ω5
= εt5.
При написании этих уравнений учтено, что проекции векторов угловой скорости и углового ускорения равны их модулям (направление оси Z совпадает с векторами ω5 и ε).
Так
как φ5
= 2πN5,
а ω5
=
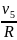 ,
то последние два уравнения запишутся
так:
,
то последние два уравнения запишутся
так:
2πN5 = , (2)
v5/R = εt5. (3)
Из
уравнения (3) найдем: t5
=
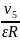 .
Подставив это выражение в (2) после
простых преобразований найдем выражение
для величины углового ускорения:
.
Подставив это выражение в (2) после
простых преобразований найдем выражение
для величины углового ускорения:
ε
=
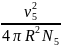 .
.
В свою очередь, если подставим полученную формулу для ε в уравнение (1) и выполним несложные преобразования, то будем иметь:
|
а1n
|
=
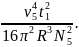 С
учетом числовых значений | а1n
|
= 1 м/с2.
С
учетом числовых значений | а1n
|
= 1 м/с2.
Ответ: |а1n| = 1 м/с2.
Задача 11. Найти величину углового ускорения ε вращающегося равноускоренно колеса, если известно, что через время t1 = 2 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол φ1 = 600 с вектором линейной скорости.
Дано: t1 = 2 с, φ1 = 600.
ε − ?
Решение.
Вначале найдем проекции полного ускорения на касательную и нормаль в момент t = t1. При этом заметим, что эти проекции равны модулям векторов соответствующих ускорений, то есть | a1τ | = a1τ и | a1n | = a1n, поскольку вектор касательного ускорения направлен в сторону касательной, а вектор нормального ускорения – в сторону нормали.
Тогда
a1τ
=
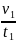 ,
а a1n
=
,
где R
– радиус вращения колеса.
,
а a1n
=
,
где R
– радиус вращения колеса.
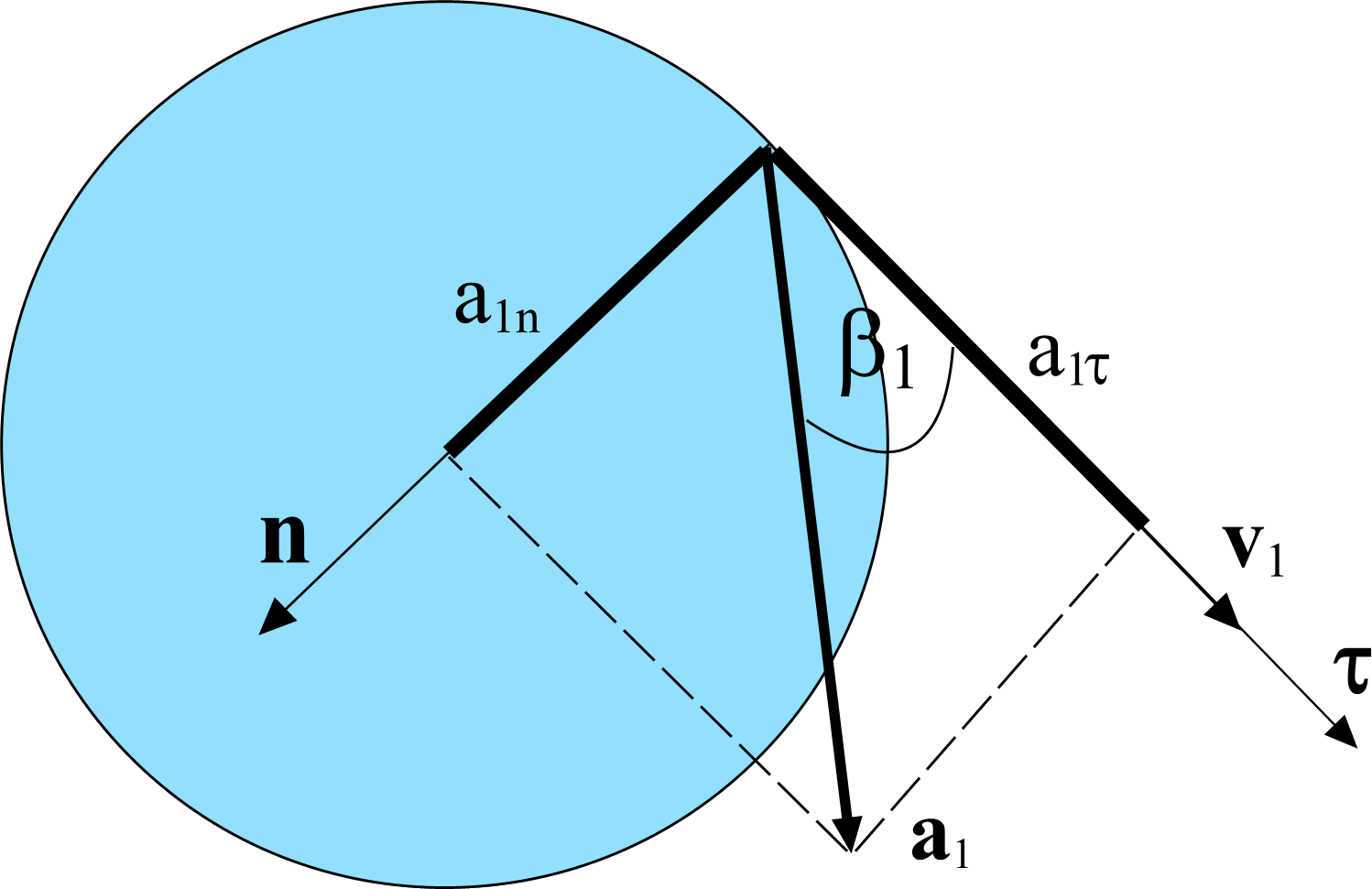
Из
рисунка видно, что
 =
tg
β1
или
tg
β1
=
=
tg
β1
или
tg
β1
=
 =
=
 .
.
Но
 = ω1,
то есть это – угловая скорость в момент
t1.
= ω1,
то есть это – угловая скорость в момент
t1.
Тогда tg β1 = ω1t1. Но ω1 = εt1, следовательно, tg β1 = ε , откуда
ε
=
 .
Подставив числа, получим: ε
= 0,43 с−2.
.
Подставив числа, получим: ε
= 0,43 с−2.
Ответ: ε = 0,43 с−2.
Гармонические колебания. Решение задач
Задача 1. Точка совершает гармонические колебания вдоль оси X по закону: x = 0,08 Cos π(t + 0,2). Определить амплитуду, период и начальную фазу колебаний.
Дано: x = 0,08 Cos π(t + 0,2).
А − ? T − ? φ0 − ?
Решение.
Запишем данное уравнение в виде x = 0,08 Cos (πt + 0,2π) и сравним его с уравнением гармонического колебания в общем виде x = А Cos (ωt + φ0). Из сопоставления этих уравнений следует, что
А = 0,08, ω = π, φ0 = 0,2π = 0,628 радиан или 360.
Поскольку
ω
=
,
то Т =
 = 2 с.
= 2 с.
Ответ: А = 0,08 м, Т = 2 с, φ0 = 360.
Задача 2. Уравнение колебаний точки имеет вид x = 0,02 Sin 5t. Определить максимальное значение vm величины скорости и максимальное значение am величины ускорения точки.
Дано: x = 0,02 Sin 5t.
vm − ? am − ?
Решение.
Проекция
скорости на ось X:
vx
=
 =
0,1 Cos
5t,
а величина скорости
=
0,1 Cos
5t,
а величина скорости
v = | 0,1 Cos 5t |. Свое максимальное значение модуль скорости примет в те моменты времени, когда косинус будет максимален, а наибольшее значение косинуса – это единица. Тогда vm = 0,1 м/с.
Проекция
ускорения на ось X:
ax
=
 = − 0,5 Sin
5t,
а величина ускорения
= − 0,5 Sin
5t,
а величина ускорения
а = 0,5 Sin 5t. Свое максимальное значение модуль ускорения примет в те моменты времени, когда синус будет максимален, а наибольшее значение синуса – это единица. Тогда аm = 0,5 м/с2.
Ответ: vm = 0,1 м/с, аm = 0,5 м/с2.
Задача 3. Точка колеблется по закону косинуса. Амплитуда колебаний А = 0,05 м, круговая частота ω = 2 с−1, начальная фаза φ0 = 0. Определить величину а1 ускорения точки в момент, когда величина ее скорости v1 = 0,08 м/с.
Дано: А = 0,05 м, ω = 2 с−1, φ0 = 0, v1 = 0,08 м/с.
а1 − ?
Решение.
Запишем уравнение гармонического колебания в общем виде: x = А Cos (ωt + φ0). С учетом данных условий задачи имеем: x = 0,05 Cos 2t. Проекция скорости на ось X: vx = = − 0,1 Sin 2t, а величина скорости равна положительному значению ее проекции, то есть v = 0,1 Sin 2t. В момент t = t1 величина скорости
v1 = 0,1 Sin 2t1 или 0,08 = 0,1 Sin 2t1. Тогда Sin 2t1 = 0,8, откуда 2t1 = 0,93
(не забывайте, что угол в системе СИ измеряется в радианах).
Проекция ускорения на ось X: аx = = 0,2 Cos 2t. Модуль ускорения равен положительному значению проекции. В момент t = t1 величина ускорения
a1 = 0,2 Cos 2t1 = 0,2 Cos 0,93.
a1 = 0,12 м/с2.
Ответ: a1 = 0,12 м/с2.
Задача 4. Точка колеблется гармонически по закону синуса. Амплитуда колебаний А = 0,1 м, максимальная величина скорости vm = 0,2 м/с, начальная фаза колебаний φ0 = 0. Написать уравнение колебаний и найти максимальную величину am ускорения точки.
Дано: А = 0,1 м, vm = 0,2 м/с, φ0 = 0.
x = x(t) − ? am − ?
Решение.
Запишем уравнение синусоидальных гармонического колебания в общем виде:
x
= А Sin
ωt.
Круговую частоту найдем из выражения
vm
= ωА:
ω
=
 .
.
ω
=
 с−1
= 2 с−1.
Тогда искомое уравнение будет выглядеть
так: x
= 0,1 Sin
2t.
с−1
= 2 с−1.
Тогда искомое уравнение будет выглядеть
так: x
= 0,1 Sin
2t.
Максимальную величину ускорения найдем из формулы am = ω2А. Подставив числа, получим: am = 0,4 м/с2.
Ответ: x = 0,1 Sin 2t, am = 0,4 м/с2.
Задача 5. Написать уравнение гармонического колебательного движения, если величина максимального ускорения точки am = 0,5 м/с2, период колебаний Т = 2 с, смещение точки от положения равновесия в начальный момент времени х0 = 0,025 м.
Дано: аm = 0,5 м/с2, Т = 2 с, х0 = 0,025 м.
x = x(t) − ?
Решение.
Запишем уравнение гармонических колебаний в общем виде, выразив его через синус:
x
= А Sin
(ωt
+ φ0).
Круговую частоту найдем по формуле ω
=
=
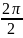 =
π.
Максимальная величина ускорения
определяется выражением аm
= ω2А.
Из этой формулы найдем амплитуду
колебаний. А =
=
π.
Максимальная величина ускорения
определяется выражением аm
= ω2А.
Из этой формулы найдем амплитуду
колебаний. А =
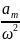 .
Подставив числа, получим:
.
Подставив числа, получим:
А = 0,05 м. Осталось найти начальную фазу φ0. Запишем уравнение гармонических колебаний для начального момента времени (t0 = 0): x0 = А Sin φ0 или 0,025 = 0,05 Sin φ0, откуда Sin φ0 = 0,5. Тогда φ0 = π/6.
Теперь можно написать искомое уравнение: x = 0,05 Sin (πt + π/6).
Эти же гармонические колебания можно выразить и через косинус, учитывая, что
Sin φ = Cos (φ – π/2). Тогда Sin (πt + π/6) = Cos (πt + π/6 – π/2). Таким образом,
x = 0,05 Cos (πt – π/3).
Ответ: x = 0,05 Sin (πt + π/6) или x = 0,05 Cos (πt – π/3).
Задача 6. Точка совершает гармонические колебания по закону косинуса с начальной фазой φ0 = 0. На расстояниях х1 и х2 от положения равновесия величина скорости точки равна соответственно v1 и v2. Найти амплитуду А и круговую частоту ω этих колебаний.
Дано: φ0 = 0, x1, x2, v1, v2.
A − ? ω − ?
Решение.
Запишем уравнение гармонических колебаний точки для моментов времени t1 и t2, когда смещения точки от положения равновесия равны соответственно х1 и х2. При этом не забудем, что φ0 = 0.
x1 = A Cos ωt1, (1)
x2 = A Cos ωt2. (2)
Запишем
выражения для проекций скоростей на
ось Х (то есть v1x
и v2x)
соответственно в моменты t1
и t2.
Поскольку v1x
=
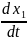 ,
а v2x
=
,
а v2x
=
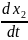 ,
то, взяв производные от обеих частей
равенств (1) и (2), получим
,
то, взяв производные от обеих частей
равенств (1) и (2), получим
v1x = − Аω Sin ωt1, (3)
v2x = − Аω Sin ωt2 (4)
Уравнения (1) – (4) дают возможность ответить на вопросы задачи. Действительно, мы имеем систему из четырех уравнений с четырьмя неизвестными: ω, A, t1, t2, то есть система может иметь решения. То, что нам по условию задачи надо найти не все неизвестные, а только два, упрощает наше решение. Правда, по условию задачи нам даны не проекции скоростей, а их модули, но пока не будем об этом думать, мы весьма корректно справимся с этим затруднением.
Вначале нам надо как-то избавиться от двух неизвестных и выйти на два уравнения с двумя неизвестными, что значительно облегчит решение. Конечно, избавляться надо от t1 и t2 (нам их все равно не надо находить). Как это сделать? Возведем в квадрат обе части уравнений (1) и (3). При этом учтем, что
(v1x)2
=
 (а
именно модуль скорости нам и задан в
условии задачи).
(а
именно модуль скорости нам и задан в
условии задачи).
x12 = A2 Cos2 ωt1, (5)
v12 = А2ω2 Sin2 ωt1. (6)
Выразим из (5) Cos2 ωt1, а из (6) Sin2 ωt1:
Cos2
ωt1
=
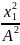 ,
Sin2
ωt1
=
,
Sin2
ωt1
=
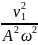 .
.
Сложим отдельно левые и правые части двух последних уравнений, и учтем, что Cos2 ωt1 + Sin2 ωt1 = 1.
+ = 1 (7).
Проделаем все то же самое с уравнениями (2) и (4). В результате получим:
 +
+
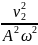 =
1 (8).
=
1 (8).
Вот мы и получили два уравнения (7) и (8) с двумя неизвестными ω и А, которые нам и надо найти.
Выразим из (7) А2ω2 и подставим полученное выражение в (8). В результате получим одно уравнение с одним неизвестным А.
Из
(7) А2ω2
=
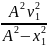 .
Простые преобразования сознательно
опущены.
.
Простые преобразования сознательно
опущены.
Подставив последнее выражение в (8), и, выполнив простые действия, будем иметь:
A
=
 .
.
Подставив последнее выражение вместо А в (7) или (8) после преобразований, получим:
ω
=
 .
Ответ: A
=
,
ω
=
.
.
Ответ: A
=
,
ω
=
.
Задача 7. Математический маятник длиной L = 2,45 м совершил n1 = 100 полных колебаний за t1 = 314 с. Определить период T колебания маятника и величину g ускорения свободного падения для данной местности.
Дано:.L = 2,45 м, n1 = 100, t1 = 314 с.
T − ? g − ?
Решение.
Период
– это время одного полного колебания,
поэтому T
=
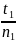 .
T
= 3,14 с.
.
T
= 3,14 с.
Период колебания математического маятника определяется формулой:
Т
= 2π∙ ,
где L
− длина нити, g
– ускорение свободного падения. Из этой
формулы находим: g
=
,
где L
− длина нити, g
– ускорение свободного падения. Из этой
формулы находим: g
=
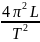 .
Подставив числа, получим: g
= 9,8 м/с2.
.
Подставив числа, получим: g
= 9,8 м/с2.
Ответ: T = 3,14 с, g = 9,8 м/с2.
Задача 8. Найти отношение L1/L2 длин двух математических маятников, если отношение периодов их колебаний T1/T2 = 1,5.
Дано:
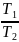 = 1,5.
= 1,5.
 −
?
−
?
Решение.
Период колебания математического маятника определяется формулой:
Т
= 2π∙
,
где ℓ − длина нити, g
– ускорение свободного падения. Тогда
для первого маятника Т1
= 2π∙ ,
для второго маятника Т2
= 2π∙
,
для второго маятника Т2
= 2π∙ .
Найдем отношение периода колебаний
первого маятника к периоду колебаний
второго:
.
Найдем отношение периода колебаний
первого маятника к периоду колебаний
второго:
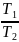 =
=
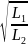 ,
откуда
=
,
откуда
=
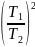 .
= (1,5)2
= 2,25.
.
= (1,5)2
= 2,25.
Ответ: = 2,25.
Задача 9. Один из маятников совершил n1 колебаний, а другой за то же время совершил n2 колебаний. Разность длин маятников L2 − L1 = ΔL. Найти длины маятников L1 и L2. Маятники считать математическими.
Дано: n1, n2, ΔL.
L1 − ? L2 − ?
Решение.
Период колебания математического маятника определяется формулой:
Т
= 2π∙
,
где L
− длина нити, g
– ускорение свободного падения. Тогда
для маятника с длиной L1:
Т1
= 2π∙
.
Для маятника с длиной L2:
Т2
= 2π∙
.
Найдем отношение периода колебаний
первого маятника к периоду колебаний
второго:
=
,
откуда
=
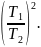
В
то же время Т1
=
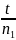 ,
а Т2
=
,
а Т2
=
 ,
где t
– время, в течение которого были совершены
,
где t
– время, в течение которого были совершены
колебания
n1
и n2.
Тогда
=
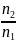 .
Следовательно,
=
.
Следовательно,
=
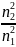 .
.
В
соответствии с условием задачи L2
= L1
+ ΔL,
тогда
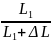 =
.
Решая последнее уравнение относительно
L1,
получим: L1
=
=
.
Решая последнее уравнение относительно
L1,
получим: L1
=
 .
Тогда
.
Тогда
L2
=
+ ΔL.
Выполнив преобразования, найдем: L2
=
 .
.
Ответ: L1 = , L2 = .
Задача 10. Маятник представляет собой шарик, прикрепленный к концу нити длиной L. При колебаниях шарик сталкивается с массивной стенкой в моменты, когда нить занимает вертикальное положение. Определить период Т колебаний маятника. Удар шарика о стенку считать абсолютно упругим. Длительностью столкновения пренебречь. Маятник считать математическим.
Дано: L.
Т − ?
Решение.
Период колебания математического маятника определяется формулой:
Тм = 2π∙ , где L − длина нити, g – ускорение свободного падения. На движение шарика из крайнего правого положения до положения равновесия (см. рисунок) будет затрачено время t′, равное четверти периода его колебаний, то есть
t′
=
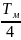 =
=
 ∙
.
∙
.
П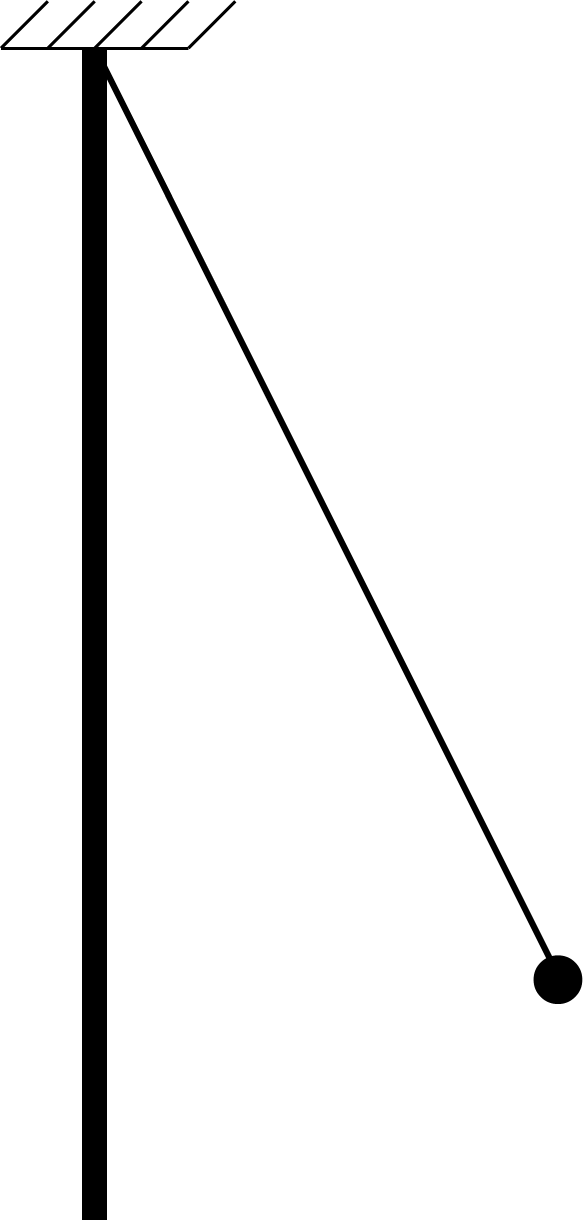 ри
абсолютно упругом ударе шарик при
отражении от стенки имеет такую же по
величине скорость, что и при ударе,
только ее направление изменится на
противоположное. Движение шарика
продолжится в обратном направлении. В
результате мы получим колебания с
периодом, равным 2t′.
Таким образом,
ри
абсолютно упругом ударе шарик при
отражении от стенки имеет такую же по
величине скорость, что и при ударе,
только ее направление изменится на
противоположное. Движение шарика
продолжится в обратном направлении. В
результате мы получим колебания с
периодом, равным 2t′.
Таким образом,
Т = π∙ .
Ответ: Т = π∙ .
Задача 11. Математический маятник длиной L1 совершает колебания вблизи вертикальной стенки. Под точкой подвеса маятника на расстоянии L2 = L1/2 от нее из стенки выступает гвоздь. Найти период Т колебаний маятника.
Дано:
L1,
L2
=
 .
.
Т − ?
Решение.
П ериод
колебания математического маятника
определяется формулой:
ериод
колебания математического маятника
определяется формулой:
Т = 2π∙ , где L − длина нити, g – ускорение свободного падения. В данном случае при колебаниях маятника его длина периодически меняется: часть времени t1 маятник имеет длину L1, другую часть времени t2 он движется, имея длину L2. Если бы маятник все время двигался с длиной L1, то период его колебаний составлял бы
Т1 = 2π∙ , а если бы его длина всегда была равна L2, то период его колебаний был бы равен Т2 = 2π∙ . Нетрудно сообразить, что период реальных колебаний маятника, то есть при наличии гвоздя, равен Т = t1 + t2. При этом t1 – это время, равное половине периода колебаний, когда длина маятника равна L1, а t2 – это время, равное половине периода колебаний, когда длина маятника равна L2.
Таким
образом, t1
=
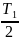 =
π∙
,
и t2
=
=
π∙
,
и t2
=
 = π∙
= π∙
= π∙
= π∙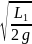 .
Период реальных колебаний маятника Т
= t1
+ t2
= π∙
+ π∙
.
.
Период реальных колебаний маятника Т
= t1
+ t2
= π∙
+ π∙
.
В результате простых преобразований получим:
Т
= π∙
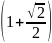 ,
что и является ответом задачи.
,
что и является ответом задачи.
Задача 12. Амплитуда колебаний математического маятника и максимальная величина скорости равны соответственно А и vm. Найти длину L маятника.
Дано: А, vm.
L − ?
Решение.
Период колебания математического маятника определяется формулой:
Т
= 2π∙
,
где L
− длина нити, g
– ускорение свободного падения. Из
этого уравнения выразим длину маятника:
L
=
 .
Колебания смещения маятника (при его
малых отклонениях от положения равновесия)
являются гармоническими. При этом Т =
,
где ω
– круговая частота колебаний. Подставив
это выражение в формулу для L,
получим: L
=
.
Колебания смещения маятника (при его
малых отклонениях от положения равновесия)
являются гармоническими. При этом Т =
,
где ω
– круговая частота колебаний. Подставив
это выражение в формулу для L,
получим: L
=
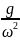 .
Круговая частота, амплитуда и максимальная
скорость при гармонических колебаниях
связаны отношением: vm
= Аω,
откуда
.
Круговая частота, амплитуда и максимальная
скорость при гармонических колебаниях
связаны отношением: vm
= Аω,
откуда
ω
=
.
Тогда L
=
 .
.
Ответ: L = .
Сложение движений. Решение задач
Задача 1. Найти величину скорости v относительно берега реки: а) лодки, идущей по течению; b) лодки, идущей против течения; c) лодки, идущей перпендикулярно течению; d) лодки, идущей под углом 300 к течению. Величина скорости течения реки u = 1 м/с, величина скорости лодки относительно воды vот = 2 м/с.
Дано: u = 1 м/с, vот = 2 м/с.
v − ?
Решение.
Свяжем с поверхностью земли условно неподвижную систему отсчета с декартовой системой координат, ось Х которой направим вдоль течения реки.
С текущей водой свяжем движущуюся систему отсчета тоже с декартовой системой координат, ось Х которой направим по течению реки (на рисунках ниже подвижная система отсчета не показана).
Разберемся со скоростями. Скорость v лодки относительно берега – это ее абсолютная скорость. Скорость vот лодки относительно воды – это ее относительная скорость. Скорость u течения реки – это переносная скорость лодки. Точнее, это скорость той точки движущейся воды, с которой совпадает лодка при своем движении (лодку, конечно, считаем перемещающейся точкой).
Записываем закон сложения скоростей: v = vот + u. Проектируем это уравнение на оси неподвижной системы отсчета: vх = vот х + uх, vy = vот y + uy. Находим проекции.
а)
лодка движется по течению реки (рисунок
а). В этом случае vот
х
= vот,
uх
= u.
Тогда vх
= vот
+ u.
Подставив числа, получим: vх
= 3 м/с. Проекции скоростей на ось Y,
очевидно, равны нулю. Величина
скорости v =
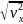 = 3 м/с.
= 3 м/с.

Рис. а Рис. b
b) лодка движется против течения реки (рисунок b). В этом случае
vот х = − vот, uх = u. Тогда vх = − vот + u. Подставив числа, получим: vх = − 1 м/с. Проекции скоростей на ось Y равны нулю. Величина скорости v = = 1 м/с.
c) лодка движется перпендикулярно течению реки (рисунок c). В этом случае
vот
х
= 0, uх
= u,
vот
y
= vот,
uy
= 0. Тогда vх
= u,
vy
= vот.
v
=
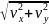 =
=
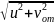 .
Подставив числа, получим: v
= 2,2 м/с. Можно найти угол α
между направлением скорости v
и направлением течения реки. Поскольку
vх
= v
Cos
α,
то
.
Подставив числа, получим: v
= 2,2 м/с. Можно найти угол α
между направлением скорости v
и направлением течения реки. Поскольку
vх
= v
Cos
α,
то
Cos
α
=
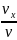 =
=
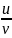 .
С учетом числовых значений Cos
α
= 0,46. Угол
α приблизительно равен 620.
.
С учетом числовых значений Cos
α
= 0,46. Угол
α приблизительно равен 620.
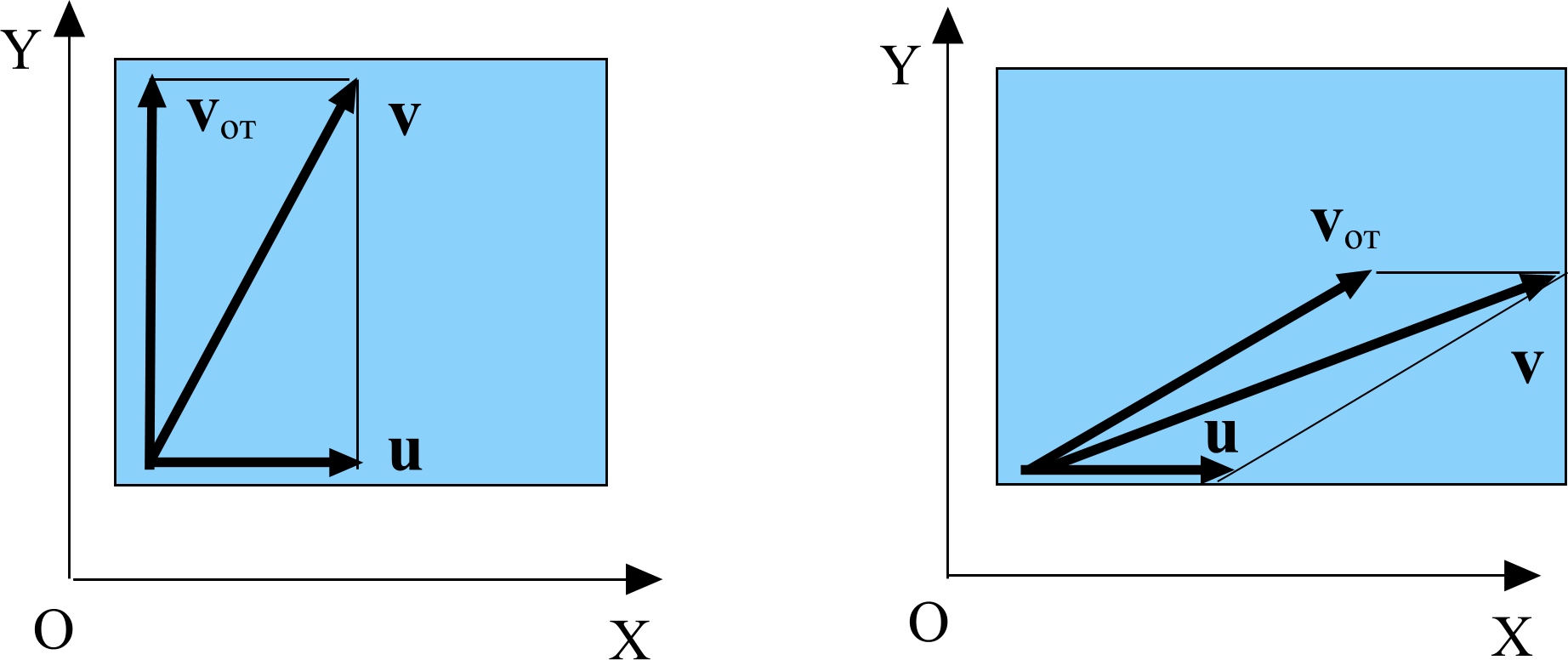
Рис. c Рис. D
d) лодка движется под углом 300 к течению (рисунок d). В этом случае
vот х = vот Cos 300, uх = u, vот y = vот Cos 600, uy = 0. После подстановки чисел, будем иметь: vот х = 1,7 м/с, uх = 1 м/с, vот y = 1 м/с. Тогда vх = 2,7 м/с, vy = 1 м/с.
Следовательно, v = = 2,9 м/с.
Ответ: а) v = 3 м/с, b) v = 1 м/с, c) v = 2,2 м/с, d) v = 2,9 м/с.
Задача 2. Самолет летит относительно воздуха со скоростью, равной по величине vот = 800 км/ч. Ветер дует с запада на восток со скоростью величиной u = 15 м/с. С какой по величине скоростью v самолет будет двигаться относительно Земли и под каким углом α к меридиану надо держать курс, чтобы перемещение было: а) на юг; b) на север; c) на запад; d) на восток.
Дано: vот = 800 км/ч = 222 м/с, u = 15 м/с.
v − ? α − ?
Решение.
Свяжем с поверхностью Земли условно неподвижную систему отсчета с декартовой системой координат, ось Х которой направим с запада на восток, то есть по направлению ветра, а ось Y − с севера на юг.
Разберемся со скоростями. Скорость v самолета относительно земли – это его абсолютная скорость. Скорость vот самолета относительно воздуха – это ее относительная скорость. Скорость u ветра – это переносная скорость.
Записываем закон сложения скоростей: v = vот + u. Направления абсолютной и переносной скоростей известны по условию задачи. Направление относительной скорости находим векторным построением, учитывая, что vот = v – u.
Проектируем закон сложения скоростей на оси неподвижной системы отсчета:
vх = vот х + uх, vy = vот y + uy. Находим проекции.
а) самолет летит на юг (рисунок а). В этом случае vх = 0,
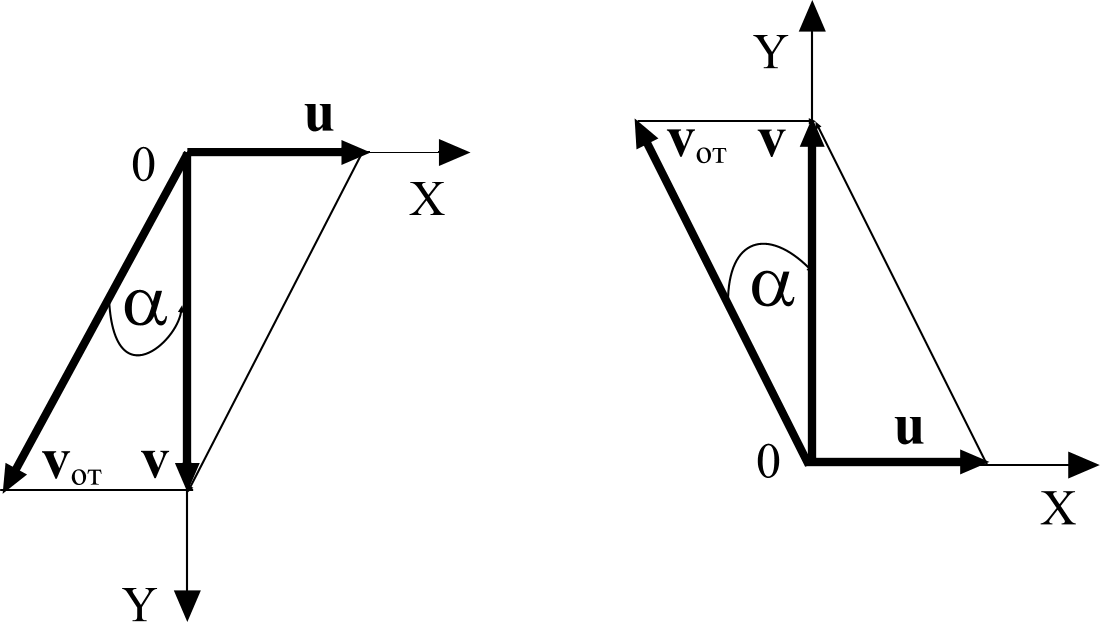
Рис. a Рис. B
vот х = vот Cos (900 + α) = − vот Sin α, uх = u, vy = v,
vот y = vот Cos α, uy = 0. Тогда
0 = u − vот Sin α,
v = vот Cos α. Запишем по-другому:
vот Sin α = u,
vот Cos α = v.
Возводим
левые и правые части двух последних
уравнений в квадрат и складываем. Учтя,
что Sin2
α
+ Cos2
α
= 1, имеем:
 =
u2
+ v2,
откуда
=
u2
+ v2,
откуда
v
=
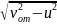 .
Подставив числа, получим: v
= 797 км/ч. Так как Sin
α
=
.
Подставив числа, получим: v
= 797 км/ч. Так как Sin
α
=
 ,
,
то
с учетом числовых значений Sin
α
=
 =
0,0676, откуда α
= 3053′.
Самолет должен держать курс на юго-запад.
=
0,0676, откуда α
= 3053′.
Самолет должен держать курс на юго-запад.
b) самолет летит на север. Ось Y также направим на север, будет удобнее находить проекции (рисунок b). В этом случае
vх = 0, vот х = vот Cos (900 + α) = − vот Sin α, uх = u, vy = v, vот y = vот Cos α, uy = 0, то есть получили такие же значения проекций, как и в первом случае. Следовательно, и значения величины абсолютной скорости и угла будут такими же. Только в этом случае самолет должен держать курс на северо-запад.
![]()
Рис. c Рис. d
c) самолет летит на запад (рисунок c). В этом случае закон сложения скоростей проектируем только на ось X, поскольку проекции всех скоростей на ось Y равны нулю. Имеем: vх = − v, vот х = − vот, uх = u. Тогда v = vот − u. Подставив числа, получим: v = 745 км/ч. Очевидно, что α = 1800. Самолет должен держать курс на запад.
d) самолет летит на восток (рисунок d). Имеем: vх = v, vот х = vот, uх = u. Тогда
v = vот + u. Подставив числа, получим: v = 853 км/ч. Очевидно, что α = 1800. Самолет должен держать курс на восток.
Ответ:
а) v = 797 км/ч, α = 3053′, курс на юго-запад;
b) v = 797 км/ч, α = 3053′, курс на северо-запад;
c) v = 745 км/ч, α = 1800, курс на запад;
d) v = 853 км/ч, α = 1800, курс на восток.
Задача 3. Лодка движется перпендикулярно к берегу со скоростью величиной vот = 7,2 км/ч относительно воды. Течение относит ее на расстояние d = 150 м вниз по реке. Найти величину u скорости течения реки и время t, затраченное на переправу через реку. Ширина реки L = 500 м.
Дано: vот = 7,2 км/ч = 2 м/с, d = 150 м, L = 500 м.
u − ? t − ?
Решение.
Лодка участвует в сложном движении. Во-первых, она движется перпендикулярно к берегу со скоростью vот относительно воды (это – относительная скорость), во-вторых, лодка переносится вместе с движущейся водой вниз по течению со скоростью u (это – переносная скорость). В результате сложения этих движений лодка перемещается относительно берега с какой-то скоростью v (это – абсолютная скорость), направленной под каким-то углом α к направлению течения воды в реке.
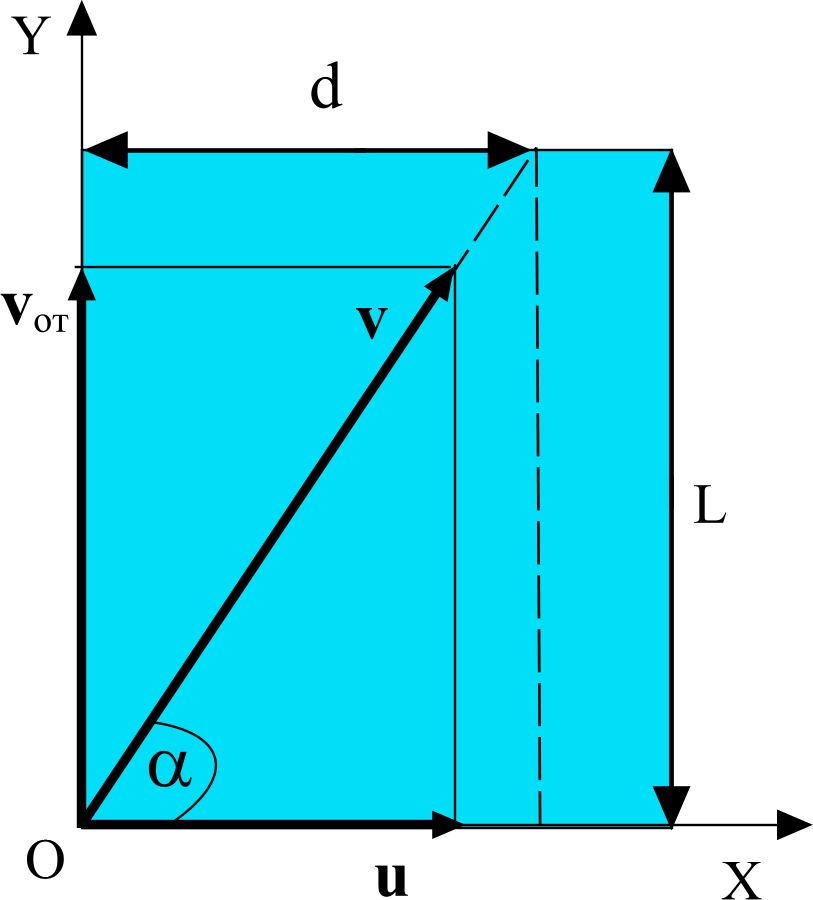
Воспользуемся законом сложения движений: v = vот + u. Проектируем это уравнение на выбранные оси (ось X направлена по течению реки, ось Y – по направлению относительной скорости, как это показано на рисунке):
vх = vот х + uх, vy = vот y + uy. Находим проекции:
vх = v Cos α, vот х = 0, uх = u, vy = v Cos (900 – α) = v Sin α, vот y = vот, uy = 0.
Тогда
v Cos α = u,
v Sin α = vот.
Поделив почленно последние уравнения друг на друга, получим: Ctg α = ,
откуда
u
= vот
Ctg
α.
В то же время Ctg
α
=
 .
Тогда u
= vот
.
.
Тогда u
= vот
.
Подставив
числа, получим: u
= 0,6 м/с. За время переправы лодка
перемещается вместе с водой на расстояние
d
со скоростью величиной u,
поэтому время, затраченное на переправу
реки, найдем по формуле: t
=
 .
С учетом числовых значений t
= 250 c.
.
С учетом числовых значений t
= 250 c.
Ответ: u = 0,6 м/с, t = 250 c.
Задача 4. Корабль идет с запада на восток со скоростью v. Известно, что ветер дует с юго-запада. Скорость ветра, измеренная на палубе корабля, равна u1. Найти величину u скорости ветра относительно земли.
Дано: v, u1.
u − ?
Решение.
Трудности, которые иногда возникают с решением задач на сложение движений (и, в частности, данной задачи) бывают связаны с непониманием того, что существует произвол в выборе условно неподвижной и подвижной систем отсчета. Другими словами, мы сами произвольны выбирать, какую систему отсчета будем считать условно неподвижной, а какую движущейся.
Если в данной задаче считать систему отсчета, связанную с землей неподвижной, а систему отсчета, связанную с ветром – движущейся, то у нас возникнут трудности с решением. Покажем это. Скорость v корабля при таком выборе систем отсчета будет являться абсолютной скоростью. Скорость u ветра – переносной скоростью. Напомню, что переносная скорость измеряется по отношению к неподвижной системе отсчета, то есть в нашем случае по отношению к земле (величину этой скорости нам и надо найти). Тогда закон сложения скоростей будет выглядеть так: v = u + vот. Здесь, vот – скорость корабля, измеренная в движущейся системе отсчета, в данном случае в системе отсчета, связанной с ветром (рисунок а). Однако эта скорость нам не известна, и не очень-то понятно, куда «приткнуть» скорость u1.
 Рис.
а
Рис.
а
Проявим гибкость в выборе систем отсчета с точки зрения того, какую систему считать условно неподвижной, а какую – движущейся. Какие у нас варианты? Их шесть (см. таблицу).
Неподвижная система отсчета |
Движущаяся система отсчета |
Земля |
Ветер |
Земля |
Корабль |
Корабль |
Земля |
Корабль |
Ветер |
Ветер |
Земля |
Ветер |
Корабль |
Тот выбор, который мы сделали изначально, соответствует первому сверху варианту таблицы. Как мы увидели, он не является удачным. Но у нас есть еще пять вариантов.
Какой же выбрать? Прочитаем еще раз условие задачи. «Скорость ветра, измеренная на палубе корабля, равна u1». Выберем в качестве движущейся системы отсчета систему, связанную с кораблем, а в качестве неподвижной – систему, связанную с землей (второй сверху вариант таблицы). Тогда роли, которые играют скорости v, u1, u, распределятся следующим образом:
v – переносная скорость (уже не абсолютная, как раньше). Она нам известна! (Еще раз настойчиво напоминаю, что переносная скорость измеряется по отношению к неподвижной системе отсчета).
u1 − относительная скорость ветра. Она измеряется по отношению к движущейся системе отсчета (к кораблю). Эта скорость нам тоже известна.
u – скорость ветра в неподвижной системе отсчета (по отношению к земле). Это – абсолютная скорость, и ее мы должны найти.
При таком «раскладе» закон сложения скоростей будет выглядеть так (рисунок b):
u = u1 + v.
Далее решаем задачу по отработанной схеме: проектируем, находим проекции… .
Выбираем оси, как показано на рисунке b.
Рис. b
ux = u1x + vx,
uy = u1y + vy.
ux
= u
Cos
450
(по условию задачи ветер дует с юго-запада).
ux
=
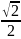 u,
u1x
= u1
Cos
α
(угол α
нам не известен, но мы потом от него
избавимся), vx
= − v,
u,
u1x
= u1
Cos
α
(угол α
нам не известен, но мы потом от него
избавимся), vx
= − v,
uy = u Sin 450 = u, u1y = u1 Sin α, vy = 0. Тогда
u = u1 Cos α − v,
u = u1 Sin α. Или
u1 Cos α = u + v,
u1 Sin α = u.
Возводим в квадрат левые и правые части двух последних уравнений, затем почленно складываем, выполняем необходимые действия и, в конце концов, приходим к уравнению:
u2
+
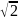 ∙vu
+ (v2
–
∙vu
+ (v2
–
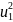 )
= 0. Решая это квадратное уравнение,
получим:
)
= 0. Решая это квадратное уравнение,
получим:
u
= −
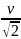 +
+
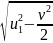 .
Знак минус перед радикалом отброшен,
поскольку модуль скорости не может быть
отрицательным.
.
Знак минус перед радикалом отброшен,
поскольку модуль скорости не может быть
отрицательным.
Ответ: u = − + .
Задача 5. Точка Р1 движется равномерно со скоростью v1 из А по направлению к В. Одновременно точка Р2 движется равномерно со скоростью v2 из В по направлению к С (см. рисунок а). Расстояние АВ = L. Острый угол АВС равен α. Определить, в какой момент времени t1 расстояние d между точками Р1 и Р2 будет минимальным и каково это расстояние.
Дано: v1, v2, L, α.
t1 − ? d − ?
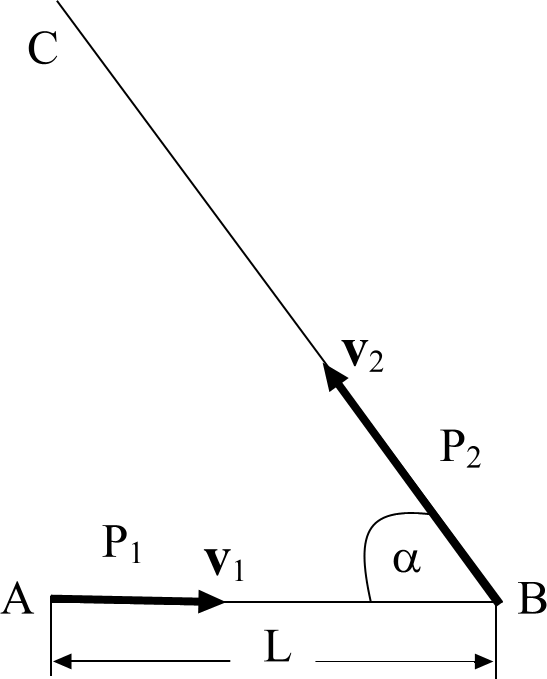
Рис.а
Решение.
Скорости движущихся точек, а также их траектории в задаче представлены по отношению к неподвижной земле, то есть указанные характеристики являются абсолютными. Нас же интересует движение точек по отношению друг к другу, например, движение точки Р2 в пространстве, связанном с точкой Р1, а не в неподвижном пространстве, связанном с землей. Но тогда (по отношению к системе отсчета, связанной с Р1) будут совсем другими и скорость точки Р2, и траектория ее движения. Если мы найдем эти относительные характеристики точки Р2, нам легче будет ответить на вопросы задачи, чем, если бы мы рассматривали движение точки Р2 в неподвижной системе и пользовались ее абсолютными характеристиками.
Выберем в качестве подвижной системы отсчета систему, связанную с точкой Р1. Тогда v1 – переносная скорость, v2 – абсолютная скорость. Применяем закон сложения скоростей и из него находим относительную скорость vот точки Р2.
v2 = v1 + vот, откуда vот = v2 − v1. Изобразим на рисунке б эту скорость vот, а также траекторию движения точки Р2 в движущейся системе отсчета точки Р1 (для точки Р2 эта система отсчета является неподвижной).
Спроектируем последнее уравнение на координатные оси (выбранные направления осей показаны на рисунке b).

Рис. b
vот х = v2х − v1х,
vот y = v2y − v1y. Находим проекции: vот х = vот Cos β,
v2х = v2 Cos α, v1х = − v1, vот y = vот Sin β, v2y = v2 Sin α, v1y = 0. Тогда
vот Cos β = v2 Cos α + v1, (1)
vот Sin β = v2 Sin α. (2)
Возводим
в квадрат левые и правые части последних
двух уравнений и почленно складываем.
После простых преобразований получим:
vот2
=
+
 +
2 v1v2
Cos
α,
откуда
+
2 v1v2
Cos
α,
откуда
vот
=
 .
.
Кратчайшим расстоянием между движущимися точками будет, очевидно, длина перпендикуляра d к линии, по которой направлена относительная скорость (эта линия является траекторией точки Р2 в системе координат, связанной с Р1).
Из
треугольника ABD
видно, что r
= L
Sin
β.
В свою очередь, из (2) Sin
β
=
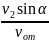 .
.
Тогда r = L или
r
= L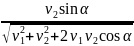 .
.
Искомое
время t1
=
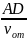 .
В свою очередь AD
= L
Cos
β.
Из (1) Cos
β
=
.
В свою очередь AD
= L
Cos
β.
Из (1) Cos
β
=
 ,
,
тогда
AD
= L
и t1
=
 .
.
t1
=
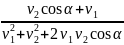 .
.
Ответ:
t1
=
,
r
= L
Задача 6. Пловец переплывает реку шириной H. Под каким углом α к течению он должен плыть, чтобы переправиться на противоположный берег за минимальное время? На какое расстояние d вниз по реке он при этом сместится? Сколько времени tmin пловец затратит на переправу, и какой путь S он в этом случае проплывет, если величина скорости течения равна u, а величина скорости пловца относительно воды равна vот?
Дано: H, u, vот.
α − ? d − ? tmin? S − ?
Решение.
Решим задачу двумя способами. Вначале рассмотрим ситуацию с точки зрения наблюдателя, покоящегося в неподвижной системе отсчета, связанной с землей. Затем посмотрим на все это глазами наблюдателя, который связан с подвижной системой отсчета, с текущей водой, и который тоже находится в покое, но уже по отношению к этой системе отсчета.
1 – й способ.
Запишем кинематическое уравнение движения пловца в неподвижной системе отсчета.
r = r0 + vt.
Абсолютная скорость пловца v = u + vот. Тогда
r = r0 + (u + vот) t. Спроектируем это равенство на координатные оси (выбор осей показан на рисунке а).
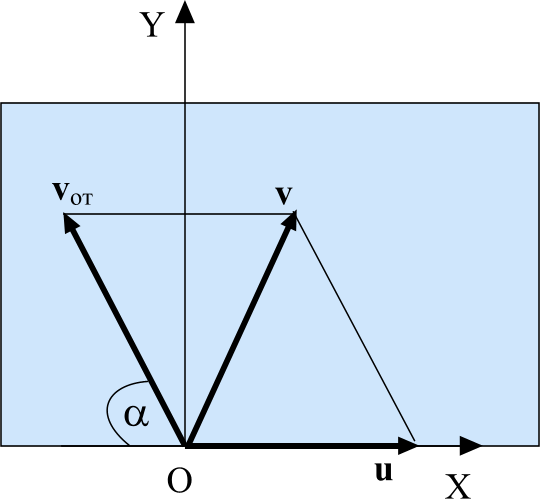
Рис. а
x = x0 + (ux + vот x) t,
y = y0 + (uy + vот y) t.
Находим проекции: x0 = 0, ux = u, vот x = vот Cos (1800 – α) = = − vот Cos α, uy = 0,
y0 = 0, vот y = vот Sin α.
Тогда,
vx = u − vот Cos α,
vy = vот Sin α.
x = (u − vот Cos α) t, (1)
y = (vот Sin α) t. (2)
Когда
пловец окажется на противоположном
берегу, его ордината будет равна H,
при этом на переправу он затратит время
tп.
Для этого момента времени уравнение
(2) следует записать так: H
= (vот
Sin
α)
tп,
откуда tп
=
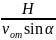 .
.
Значение
tп
будет минимальным, если Sin
α
максимален, то есть равен единице, а это
значение синус имеет при α
= 900.
Отсюда tmin
=
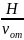 .
.
Уравнение (1) в этом случае примет вид:
x1 = (u − vот Cos 900) tmin или x1 = u .
Очевидно, что смещение d пловца вниз по реке будет по величине равно его координате x1, то есть d = u .
Таким образом, чтобы переплыть реку за минимальное время, пловец должен плыть с относительной скоростью vот, перпендикулярной к берегу (рисунок b).
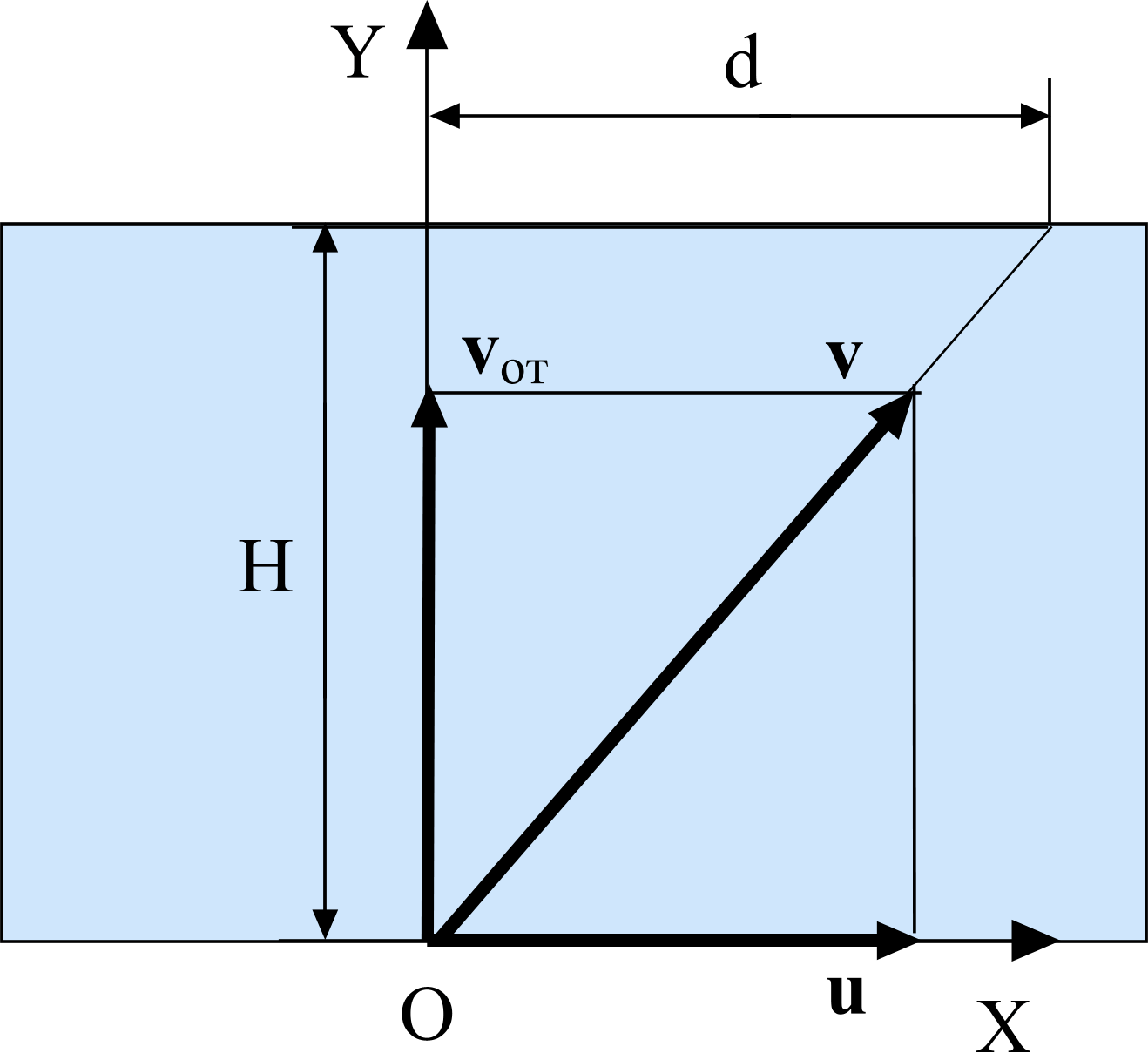
Рис. b
При этом проекции абсолютной скорости на координатные оси будут:
vx = u, так как Cos 900 = 0,
vy = vот, так как Sin 900 = 1. (Обозначения проекций абсолютной скорости и в дальнейшем ее модуля для этого частного случая, когда α = 900, оставлены прежними для упрощения математической записи формул).
Модуль абсолютной скорости v = = .
Тогда S = v tmin или Тогда S = .
2 – й способ.
Теперь перейдем в систему отсчета, связанную с движущейся со скоростью u водой. В этой системе отсчета вода в реке неподвижна, и пловец переправится на противоположный берег за минимальное время, если будет плыть со скоростью vот перпендикулярно берегам. Этот факт очевиден. Минимальное время будет при этом равно tmin = .
Естественно, что в этой системе отсчета ни о каком смещении пловца по течению воды говорить не приходится, поскольку вода для него неподвижна. Путь же, который проделает пловец в этой системе, очевидно, равен Н. Таким образом, наблюдатель, находящийся в движущейся системе отсчета в принципе ничего не может знать ни о каком другом пути S, ни о каком смещении d пловца, поскольку и S и d «работают» в неподвижной системе, и этот наблюдатель может о ней ничего и не знать. А ежели знает, то есть, например, видит землю, то она для него будет являться движущейся системой, и он увидит, что его коллега (наблюдатель, стоящий на земле) смещается в направлении, перпендикулярном направлению движения пловца. И смещение это будет равно по величине, но направлено противоположно смещению пловца, которое видит «земной» наблюдатель.
Ответ: α = 900; d = u ; tmin = ; S = .
Задача 7. Два катера одновременно отошли от причалов А и В, находящихся на противоположных берегах реки, и движутся все время по прямой АВ, соединяющей причалы. Расстояние между причалами АВ = 1 км. Прямая АВ образует с направлением течения воды в реке угол α = 600. Величина скорости течения воды по всей ширине реки одинакова и равна u = 2 м/c. Определить: координаты xв, yв места встречи катеров; угол β по отношению к прямой АВ, под которым они должны двигаться, чтобы оставаться на этом курсе; величину vот скорости движения катеров относительно неподвижной воды (считать, что по величине эта скорость одна и та же для каждого катера), если известно, что катера встретились через tв = 3 мин после их отхода от причалов.
Дано: АВ = 1 км = 1000 м; α = 600; u = 2 м/c; tв = 3 мин = 180 с.
xв − ? yв − ? β − ? vот − ?
Решение.
Решение выполним в условно неподвижной системе отсчета, связанной с землей.
При решении данной задачи воспользуемся законом движения (кинематическим уравнением движения) и законом сложения скоростей. В общем-то, в основном все задачи кинематики решаются только с использованием этих законов. Другое дело, что в некоторых случаях нет необходимости в применении сразу двух этих законов, нередко бывает, что хватает какого-то одного из них.
Для катера, отходящего от причала А:
rA = r0A + vAt,
vA = vот A + u.
Для катера, отходящего от причала B:
rB = r0B + vBt,
vB = vот B + u.
Здесь, vA и vB – абсолютные скорости катеров, vот A и vот B – их относительные скорости, u – переносная скорость.
Как обычно, векторные уравнения проектируем на координатные оси декартовой системы координат. Решение задачи значительно упростится, если направления осей выбрать так, как показано на рисунке. Начало системы отсчета совместим с причалом А.

В результате проектирования мы получим восемь уравнений, которые и позволят ответить на вопросы задачи. Однако часто бывает, что для решения задачи достаточно использовать лишь часть этих уравнений. Проектируем уравнения в той последовательности, как они записаны выше.
xA = x0A + vAxt,
vAx = vот A x + ux,
vAy = vот A y + uy,
xB = x0B + vBxt,
vBх = vот B x + ux.
Обратите внимание, мы ограничились пятью уравнениями. А почему не записали все восемь? Кинематические уравнения движения мы не проектировали на ось Y, поскольку все кинематические характеристики этих уравнений перпендикулярны оси Y и в проекциях дадут нули. В этом наша «заслуга»: мы удачно выбрали ориентацию координатных осей и сэкономили на двух уравнениях. Кроме того мы не выполнили проектирование на ось Y закона сложения скоростей для катера, отходящего от причала В. Почему? Дело в том, что после нахождения проекций мы получим такое же уравнение, как и для катера, отходящего от причала А (можете проверить), а зачем нам два одинаковых уравнения?
Итак, находим проекции: x0A = 0, vAx = vA, vот A x = vот Cos β (мы не написали vот A, а написали vот, поскольку по условию задачи vот A = vот A = vот), ux = u Cos α,
vAy = 0, vот A y = vот Sin β, uy = u Cos (900 + α) = − u Sin α, x0B = S, vBx = − vB,
vот B x = vот Cos (1800 − β) = − vот Cos β.
Подставляем найденные проекции и получаем:
xA = vAt, (1)
vA = vот Cos β + u Cos α, (2)
0 = vот Sin β − u Sin α, (3)
xB = S − vB t, (4)
− vB = − vот Cos β + u Cos α. (5)
Вот в этих пяти уравнениях и скрыты ответы на вопросы задачи. Займемся поисками этих ответов.
В момент t = tв координаты катеров будут одними и теми же. Тогда правые части уравнений (1) и (4) будут равны друг другу, то есть
vAtв = S − vB tв.
Модули абсолютных скоростей дают нам уравнения (2) и (5). Тогда
(vот Cos β + u Cos α) tв = S – (vот Cos β −u Cos α) tв.
Раскрыв скобки и выполнив простые действия, получим:
Cos
β =
 (6)
(6)
Из уравнения (3) имеем:
Sin
β
=
 (7)
(7)
Делим почленно (7) на (6) и получаем:
tg
β =
 .
Подставив
численные значения, получим tg
β
≈ 0,624; β
≈ 320.
.
Подставив
численные значения, получим tg
β
≈ 0,624; β
≈ 320.
Величину относительной скорости катеров можно найти из (6) или из (7).
Из
(6): vот
=
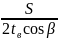 .
.
С учетом числовых значений vот ≈ 3,3 м/с (Cos 320 = 0,848).
Наконец, найдем координаты встречи катеров. Ордината нам уже известна: мы так выбрали ориентацию системы координат, что yв = 0. Абсциссу найдем из (1). В момент встречи xв = vAtв. Модуль скорости vA находим из (2). После подстановки чисел, получим:
vA = 3,8 м/с.
xв = 684 м.
Ответ: xв = 684 м; yв = 0; β ≈ 320; vот ≈ 3,3 м/с.
Задача 8. В бассейне по трем дорожкам плывут пловцы: по второй и третьей дорожкам в одну сторону, а по первой – в противоположную. Модули скоростей первого и второго пловцов равны соответственно v1 и v2. Найти величину v3 скорости третьего пловца, если все время пловцы находятся на одной прямой и плывут по середине дорожек. Расстояния между серединами дорожек одинаковы.
Дано: v1, v2.
v3 − ?
Решение.
Решение будет проще, если его выполнить в условно неподвижной системе отсчета, связанной с первым пловцом.
В выбранной системе отсчета дадим кинематическим характеристикам пловцов следующие обозначения:
r2 – радиус-вектор второго пловца,
r20 – начальный радиус-вектор второго пловца,
r3 – радиус-вектор третьего пловца,
r30 – начальный радиус-вектор третьего пловца,
v2от – скорость второго пловца в системе отсчета, связанной с первым пловцом,
v3от – скорость третьего пловца в системе отсчета, связанной с первым пловцом.
Все перечисленные характеристики – относительные, однако, чтобы не загромождать индексами математические формулы, индексы от у радиус-векторов сознательно опущены.
Записываем закон движения и закон сложения скоростей для второго и третьего пловцов.
r2 = r20 + v2отt,
r3 = r30 + v3отt,
v2 = v2от + v1,
v3 = v3от + v1.
При написании последних двух формул учтено, что v2 и v3 – это абсолютные скорости второго и третьего пловцов соответственно, а v1, которая в системе отсчета, связанной с бассейном, является абсолютной скоростью, теперь уже при нашем выборе системы отсчета, будет представлять собой переносную скорость.
Проектируем написанные уравнения на координатные оси, ориентация которых показана на рисунке. Рисунок сделан для движущейся системы отсчета и для случая, когда величина скорости первого пловца меньше величин скоростей второго и третьего (в противном случае v2от и v3от были бы направлены в противоположную сторону).
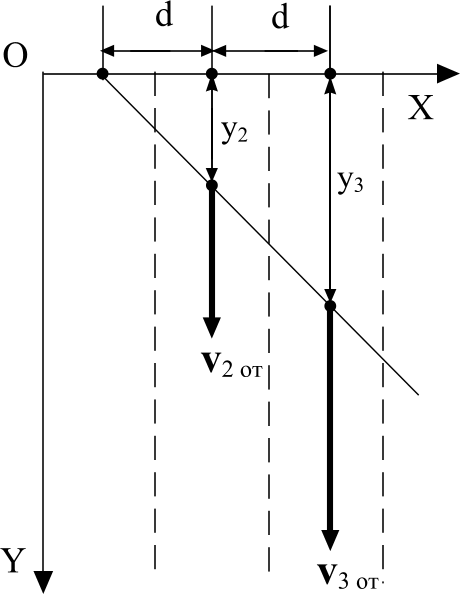
y2 = y20 + v2от yt,
y3 = y30 + v3от yt,
v2y = v2от y + v1y,
v3y = v3от y + v1y.
За начало отсчета времени удобно взять момент, когда пловцы ныряют в воду. Находим проекции:
y20 = 0, v2отy = v2от, y30 = 0, v3от y = v3от, v2y = v2, v1y = − v1, v3y = v3. Тогда
y2 = v2от t, (1)
y3 = v3от t, (2)
v2 = v2от − v1, (3)
v3 = v3от − v1. (4)
Из уравнений (3) и (4) v2от = v2 + v1, v3от = v3 + v1. С учетом этого, уравнения (1) и (2) примут вид:
y2 = (v2 + v1) t, y3 = (v3 + v1) t.
Поделив почленно последние два уравнения друг на друга, получим:
 =
=
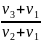 .
Но
=
.
Но
=
 = 2 (из подобия треугольников),
= 2 (из подобия треугольников),
d – расстояние между пловцами. Тогда
= 2. Отсюда легко находим искомую скорость.
v3 = 2v2 + v1.
Ответ: v3 = 2v2 + v1.
Задача 9. Равносторонний треугольник со стороной r = 1 м вращается в плоскости рисунка вокруг точки O с постоянной угловой скоростью величиной ω = 4 с−1. По стороне АВ равномерно движется точка со скоростью величиной vот = 3 м/с относительно треугольника. Найти модули абсолютной скорости и абсолютного ускорения точки в тот момент, когда она попадет в положение В.
Дано: а = 1 м, ω = 4 с−1, vот = 3 м/с.
v − ? а − ?
Решение.
Переносная скорость u точки направлена перпендикулярно радиусу окружности, по которой вращается треугольник, то есть перпендикулярно АВ. Относительная скорость vот направлена вдоль стороны 0В треугольника.
В соответствии с законом сложения скоростей абсолютная скорость v = u + vот (рис. а).

Рис. а
Модуль абсолютной скорости является диагональю параллелограмма Вuvvот. Легко видеть, угол α = 1500 (не забывайте, что вращающийся треугольник – равносторонний, значит, все его углы равны 600).
Таким образом, задача нахождения модуля скорости v сводится к нахождению диагонали параллелограмма по известным сторонам и углу между ними. Применив известную формулу, найдем:
v
=
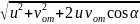 .
Эта формула довольно часто встречается
при решении различных физических задач,
поэтому, полезно не надеяться на свою
память, а уметь эту формулу получить.
.
Эта формула довольно часто встречается
при решении различных физических задач,
поэтому, полезно не надеяться на свою
память, а уметь эту формулу получить.
Предложу два способа получения этой формулы.
Первый способ удобен тем, что при нем соблюдается та последовательность в решении задач, которую мы всегда использовали: записываем векторное уравнение, проектируем на выбранные оси, находим проекции и так далее. То есть, при этом Вам ничего нового выдумывать не надо.
Итак, выбираем оси.
Пусть ось Х направлена по радиусу вращения (вдоль 0В), а ось Y – перпендикулярно ей (вдоль переносной скорости u). Проектируем закон сложения скоростей на эти оси:
vx = ux + vот x,
vy = uy + vот y.
Находим проекции:
ux = 0, vот x = vот Cos (α – 900) = vот Sin α, uy = u, vот y = vот Cos α.
Тогда vx = vот Sin α,
vy = u + vот Cos α.
Находим квадраты проекций и складываем их:
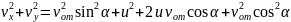 .
.
Учитывая,
что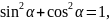 получаем:
получаем:

Поскольку
v
=
,
то v
=
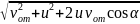 .
.
Второй способ удобен своей простотой. Возведем в квадрат обе части векторного уравнения сложения скоростей:
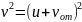 или
или
 .
.
Квадрат вектора есть квадрат его модуля, то есть v2 = v2, u2 = u2. Скалярное произведение векторов равно произведению их модулей и косинуса угла между ними, то есть uvот = uvот Cos α.
Тогда v = .
Переносная скорость u = ω·0В = ω·r.
Тогда
v
=
 .
.
Подставив числа, получим v = 2 м/с (Cos 1500 = − 0,866).
Перейдем к ускорениям. Относительное движение – равномерное и прямолинейное, следовательно, относительное ускорение равно нулю. Вращательное (оно же переносное) движение – тоже равномерное, следовательно, касательное ускорение равно нулю. Поэтому полное ускорение переносного движения – это нормальное ускорение аn. Поскольку точка обладает относительной скоростью, то будет присутствовать еще и ускорение Кориолиса акор. Полное абсолютное ускорение а точки представляет собой векторную сумму всех ее ускорений. В данном случае а = аn + акор. Разберемся с направлениями ускорений. С нормальным ускорением все просто, оно направлено к центру вращения. Для нахождения направления кориолисова ускорения, следует вспомнить, что акор = ωхvот, поэтому его направление определяется по правилу нахождения направления векторного произведения. Однако есть способ, предложенный Н.Е. Жуковским, позволяющий проще найти ориентацию акор. Надо мысленно повернуть вектор относительной скорости на 900 в направлении вращения, и он укажет направление ускорения Кориолиса. На рисунке b вектор vот показан пунктиром.

Рис. b
Несложно найти угол между аn и акор, он равен α = 1500. Тогда
а
=
 .
Модуль нормального ускорения аn
= ω2r,
модуль кориолисова ускорения
.
Модуль нормального ускорения аn
= ω2r,
модуль кориолисова ускорения
акор = ωv Sin 900 = ωv.
Выполнив необходимые вычисления, найдем: аn = 16 м/с2, акор = 12 м/с2, а = 8 м/с2.
Ответ: v = 2 м/с, а = 8 м/с2.
Задача 10. Используя метод векторных диаграмм, сложить гармонические колебания x1 = A1 Cos (ωt + φ01) и x2 = A2 Cos (ωt + φ02), то есть найти амплитуду А и начальную фазу φ0 результирующего движения. А1, А2, ω, φ01, φ02 считать известными.
Дано: x1 = A1 Cos (ωt + φ01), x2 = A2 Cos (ωt + φ02).
А − ? φ0 − ?
Решение.
Первое гармоническое колебание можно представить как движение проекции конца радиус-вектора A1, составляющего с осью Х угол φ01 в начальный момент времени и вращающегося по окружности с угловой скоростью ω.
Точно также второе гармоническое колебание можно представить как движение проекции конца радиус-вектора A2, составляющего с осью Х угол φ02 в начальный момент времени и вращающегося по окружности с той же угловой скоростью ω.
Действительно, если, например, в начальный момент времени t0 проекция х10 вектора А1 была х10 = A1 Cos φ01, то, спустя время t, его проекция х1 = A1 Cos φ1.
Очевидно, что φ1 представляет собой сумму двух углов: угла φ01, который составлял вектор А1 в начальный момент времени и угла φ′, который вектор накрутил за время t, то есть φ1 = φ01 + φ′ (рисунок а). Угол же φ′ равен величине ω угловой скорости вращения вектора, умноженной на время, за которое вектор повернулся на этот угол, то есть φ′ = ωt.

Рис. а
Тогда φ1 = φ01 + ωt и x1 = A1 Cos (ωt + φ01). Аналогичные рассуждения можно провести и в отношении вектора А2: φ2 = φ02 + ωt, x2 = A2 Cos (ωt + φ02).
Сложив векторы А1 и А2, мы получим какой-то вектор А, проекция х которого будет равна сумме х1 и х2, то есть х = х1 + х2 (рис. b).
Конечно, это сложение можно сделать и чисто аналитически, то есть записать выражение х = A1 Cos (ωt + φ01) + A2 Cos (ωt + φ02), а затем с помощью тригонометрических преобразований ответить на поставленные в задаче вопросы. Именно так мы и поступали в параграфе 3.16. С помощью же векторных диаграмм все значительно упрощается. Сейчас мы получим те же результаты, что и в указанном параграфе, затратив на это гораздо меньше усилий.
Из рисунка b видно, что х = А Cos φ. При этом φ = ωt + φ0 (исходя из подобных рассуждений, что мы делали для вектора А1).
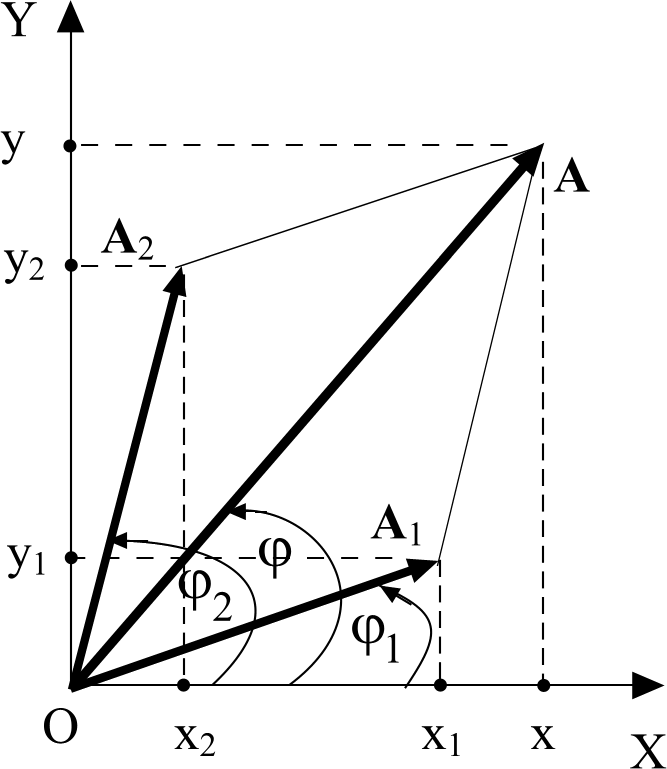
Рис. b
Тогда х = A Cos (ωt + φ0). Амплитуду А находим как диагональ параллелограмма ОА2АА1 по известной формуле:
А
=
 .
Поскольку φ2
– φ1
= φ02
– φ01,
то
.
Поскольку φ2
– φ1
= φ02
– φ01,
то
А
=

Начальную фазу φ0 можно найти по тангенсу этого начального угла. Очевидно, что для любого угла φ его тангенс tg φ = (см. рисунок b) Но
y = y1 + y2 = A1 Sin φ1 + A2 Sin φ2, а
x
= x1
+ x2
= A1
Cos φ1
+ A2
Cos φ2.
Тогда
tg
φ
= .
.
Это выражение справедливо для любого момента времени, в том числе, и начального, то есть
tg
φ0
=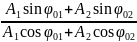 .
Тогда
начальный угол (начальная фаза)
.
Тогда
начальный угол (начальная фаза)
φ0 = arctg .
Ответ:
А =
 ,
φ0
= arctg
.
,
φ0
= arctg
.
Глава 12. Задачи на динамику
Во всех, решаемых нами задачах на динамику, считать, что сила сопротивления воздуха равна нулю, а величина ускорения свободного падения вблизи поверхности Земли g = 10 м/с2 (если не будет других указаний).
§ 12.1. Поступательное движение
Задача 1. К тонкой, невесомой и нерастяжимой нити подвешен груз массой m = 1 кг. Найти величину силы натяжения Т нити, если нить с грузом: а) поднимать с ускорением величиной а = 5 м/с2; б) опускать с тем же по величине ускорением.
Дано: m = 1 кг, а = 5 м/с2.
Т − ?
Решение.
Рассмотрим силы, действующие на груз.
Груз взаимодействует с двумя объектами: с Землей и нитью. Поэтому на него будут действовать только две силы. Сила, действующая со стороны Земли – это сила тяжести Fт = mg. Сила, действующая со стороны нити – это сила реакции нити Q. Теперь – внимание! Очень часто (практически всегда) эту силу (силу реакции нити) называют силой натяжения нити и считают, что именно ее и надо найти по условию задачи. И обозначают ее, как правило, Т. Однако это совсем не так. Действительно, в задаче надо найти силу натяжения нити Т. Как проявляется действие этой силы? Очевидно (даже, судя по названию), она натягивает нить. К чему должна быть приложена эта сила, чтобы натягивать нить? Что за вопрос, к нити, конечно, не к Луне же! А к чему приложена сила Q? Эта сила приложена к грузу (рис. а), и поэтому она ну, никак не может натягивать нить! Как же быть? Как найти силу Т, которая приложена к нити и натягивает ее?
Все очень просто, надо вспомнить третий закон Ньютона: если нить действует на груз с силой реакции Q, то и груз действует на нить с такой же по величине силой, только направленной в противоположную сторону. Таким образом Q = Т, Q = − Т. На рисунке а показаны все силы, действующие на груз, а на рисунке b – сила, действующая на нить со стороны груза. Другие силы, приложенные к нити, например, сила, действующая на нить со стороны какого-то объекта, заставляющая ее двигаться, нам не интересны и потому не показаны.

Рис. a Рис. b Рис. с Рис. d
Записываем второй закон динамики для груза:
mg + Q = ma.
У Вас уже накоплен приличный опыт решения задач по кинематике, и Вы знаете, что появившееся векторное уравнение надо проектировать.
Движение объектов происходит вдоль одной оси, поэтому и проектировать будем на одну ось. Назовем ее осью Y и направим, например, вертикально вверх.
а) нить с грузом движутся вверх (рис. c).
mgy + Qy = may. Находим проекции: gy = − g, Qy = Q, ay = а. Тогда
− mg + Q = ma, откуда Q = m (g + a). С учетом третьего закона динамики Q = T, поэтому
Т = m (g + a).
Подставив числа, найдем Т = 15 Н.
б) нить с грузом движутся вниз (рис. d).
Находим проекции: gy = − g, Qy = Q, ay = − а. Тогда
− mg + Q = − ma, откуда Q = m (g − a).
С учетом третьего закона динамики Т = m (g − a).
Подставив числа, найдем Т = 5 Н.
Надеюсь, Вы убедились, что без применения третьего закона Ньютона эту задачу просто не решить, но ведь умудряются…
Ответ: а) Т = 15 Н, б) Т = 5 Н.
Задача 2.Тело массой m = 10 кг движется равнозамедленно по горизонтальной плоскости. Найти величину ускорения а тела, а также величину и направление силы R, с которой плоскость действует на тело, если коэффициент трения k = 0,5. Сколько времени t1 тело будет двигаться до остановки, и какое по величине перемещение r1 за это время оно совершит, если в момент начала наблюдения величина скорости тела v0 = 15 м/с.
Дано: m = 10 кг, k = 0,5, v0 = 15 м/с.
a − ? R − ? t1 − ? r1 − ?
Решение.
Определим силы, действующие на тело.Тело взаимодействует с двумя объектами: с Землей и горизонтальной плоскостью, которая является связью. Поэтому на него будут действовать только две силы. Сила, действующая со стороны Земли – это сила тяжести Fт = mg. Сила, действующая со стороны плоскости – это сила реакции R. В общем случае нахождение величины и направления сил реакции представляет собой очень трудную, а иногда и теоретически неразрешимую задачу. В таких случаях эти силы находятся экспериментально. В редких случаях (данная задача как раз к ним относится) этот вопрос решается просто. Для этого применяют следующий прием. Раскладывают силу реакции на две составляющие, одна из которых направлена перпендикулярно связи (в данном случае перпендикулярно горизонтальной плоскости), а другая – вдоль движения тела в сторону, противоположную направлению его скорости (см. рисунок). Первую составляющую называют силой нормальной реакции связи и обычно обозначают Q или N, а вторую называют силой трения и обозначают Fтр. Вообще-то разложить любую силу мы можем по любым направлениям. Почему силу реакции R мы раскладываем именно по таким направлениям, о которых говорилось выше, а не по другим, будет понятно из дальнейшего.
Записываем второй закон Ньютона для тела: mg + R = ma. Поскольку R = N + Fтр, то : mg + N + Fтр = ma. Силы, действующие на тело, располагаются в плоскости, поэтому проектировать последнее уравнение следует на две оси. Пусть направление осей такое, как показано на рисунке.
mgx + Nx + Fтр x = max,
mgy + Ny + Fтр y = may.

Находим проекции:
gx = 0, Nx = 0, Fтр x = − Fтр, ax = − а, gy = − g, Ny = N, Fтр y = 0, ay = 0. Тогда
− Fтр
= − ma,
откуда а =
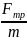 .
.
− mg + N = 0, откуда N = mg.
Казалось
бы мы не приблизились к решению, поскольку
сила трения нам не известна, а последнее
уравнение никакого отношения к силе
трения не имеет. Имеет! Дело в том, что
экспериментально найдено, что модули
составляющих сил реакции, то есть Fтр
и N
связаны между собой следующей зависимостью:
Fтр
= kN,
где k
называется коэффициентом трения (часто
его обозначают буквой µ). Именно
поэтому-то, заранее зная эту связь, мы
и раскладывали силу реакции по указанным
направлениям. Эта связь называется
законом Амонтона-Кулона. Тогда Fтр
= kmg
и а =
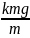 = kg.
Подставив числа, получим: а = 5 м/с2.
= kg.
Подставив числа, получим: а = 5 м/с2.
Модуль силы реакции
R
=
 =
=
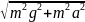 = m
= m
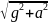 .
С учетом числовых значений
.
С учетом числовых значений
R = 112 Н.
Направление силы R найдем по углу α.
Cos
α =
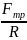 =
= .
Подставив
числа, найдем: Cos
α
= 0,446, откуда α
= 63,50.
.
Подставив
числа, найдем: Cos
α
= 0,446, откуда α
= 63,50.
Ответы на последние два вопроса дает кинематика. Сразу запишем уравнение движения и уравнение для скорости в модулях для момента t = t1 (если Вы добросовестно решали предыдущие кинематические задачи, для Вас это не составит никакого труда).
r1 = v0t1 − ,
0 = v0 − аt1.
Решив эту систему уравнений и подставив числа, получим: t1 = 3 с, r1 = 22,5 м.
Ответ: a = 5 м/с2, R = 112 Н, α = 63,50, t1 = 3 с, r1 = 22,5 м.
Задача 3. Два тела с массами m1 = 1кг и m2 = 4 кг, соединенные нерастяжимой невесомой нитью, лежат на горизонтальной плоскости. С каким по величине ускорением а будут двигаться тела, если к одному из них приложить силу величиной F = 10 Н, направленную горизонтально? Какова будет величина Т силы натяжения нити, если эту силу приложить: а) к телу с массой m1; б) к телу с массой m2? Трением пренебречь.
Дано: m1 = 1кг, m2 = 4 кг, F = 10 Н.
а − ? Т − ?
Решение.
а) сила F приложена к телу с массой m1 (будем называть его первым телом).
Первое тело взаимодействует с четырьмя объектами: с Землей, плоскостью, нитью (нить и плоскость являются связями) и с каким-то телом (каким – неважно), обеспечивающим появление силы F (назовем ее внешней силой). Поэтому на первое тело будут действовать четыре силы. Помимо силы F это − сила тяжести, сила реакции плоскости и сила реакции нити. Со вторым телом все также за исключением силы F. Поскольку сила трения по условию задачи отсутствует, то сила реакции плоскости для каждого тела будет ей перпендикулярна, то есть будет являться силой нормальной реакции. Так как для каждого тела эта сила и сила тяжести равны по величине, действуют вдоль одной прямой в противоположные стороны, то они уравновешивают друг друга и не оказывают влияния на ускорение тел и силу натяжения нити. Поэтому, чтобы не усложнять рисунок, эти силы на нем мы отображать не будем.
На рисунке а представлены силы, действующие по горизонтали на каждое тело.
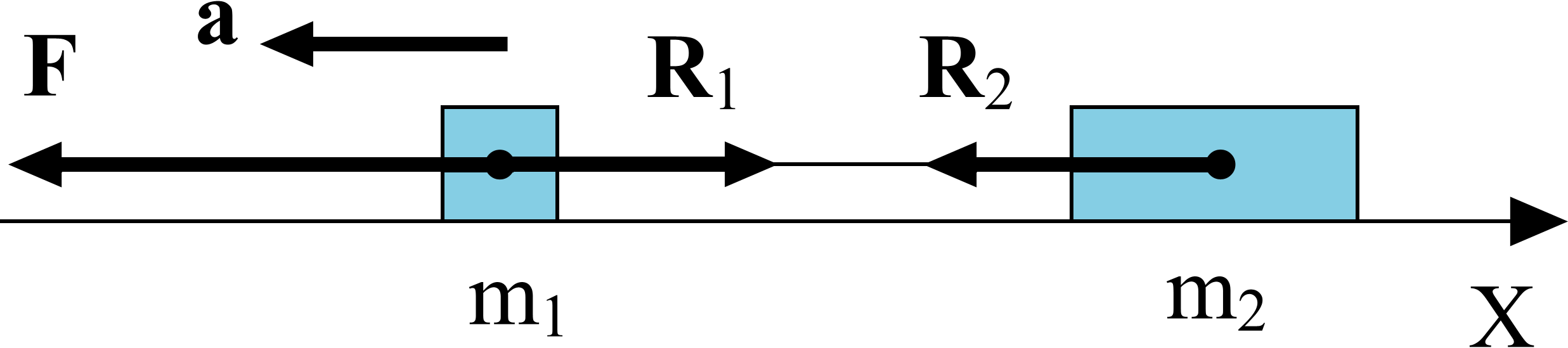
Рис. а
R1 – сила реакции нити, действующая на первое тело,
F – внешняя сила (сейчас она приложена к первому телу),
R2 – сила реакции нити, действующая на второе тело.
Записываем второй закон Ньютона для каждого тела сразу в проекциях на горизонтальную ось X (направление оси показано на рисунке):
Fx + R1х = m1a1х,
R2х = m2a2х.
После нахождения проекций, будем иметь:
− F + R1 = − m1a1,
− R2 = − m2a2.
При нахождении проекций было учтено, что ускорения тел направлены в сторону силы F, что очевидно.
По третьему закону Ньютона величина силы, с которой нить действует на тело с массой m1, равна величине силы, с которой это тело действует на нить (это – сила натяжения нити Т1), то есть R1 = Т1. Аналогично R2 = Т2. Тогда предыдущие уравнения примут вид:
− F + Т1 = − m1a1, (1)
− Т2 = − m2a2. (2)
Имеем два уравнения с четырьмя неизвестными (Т1, a1, Т2, a2).
Избавиться от двух неизвестных нам поможет условие о невесомости и нерастяжимости нити. Действительно, если нить нерастяжима (жесткая), то каждый ее участок (а, значит, и тела, прикрепленные к концам нити) движутся с одинаковыми по величине ускорениями, то есть a1 = a2 = а. Посмотрим, что нам даст условие невесомости нити. Запишем второй закон Ньютона для нити: Т1 + Т2 = mнан. Невесомость нити означает равенство нулю ее массы (mн = 0), тогда
Т1 + Т2 = 0.
В проекциях на ось X (рис. b) имеем:
![]()
Рис. b
Т1х + Т2х = 0 или Т2 − Т1 = 0, откуда
Т1 = Т2 = Т.
Уравнения (1) и (2) теперь можно записать так:
F − Т = m1a, (3)
Т = m2a. (4)
Теперь мы имеем два уравнения с двумя неизвестными (а и Т). Сложим левые и правые части этих уравнений:
F
= a
(m1
+ m2),
откуда а =
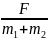 .
Из (4) находим Т: Т =
.
Из (4) находим Т: Т =
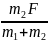 .
Подставив числа, получим: а = 2 м/с2,
Т = 8 Н.
.
Подставив числа, получим: а = 2 м/с2,
Т = 8 Н.
б) сила F приложена к телу с массой m2 (рис. c).
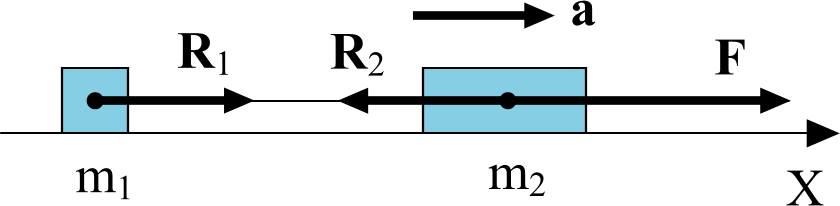
Рис. с
Проводим аналогичные рассуждения, как для случая а). В результате имеем:
T
= m1a,
F
– T
= m2a.
Решив систему, получим: а =
(то есть то же самое, что и в первом
случае), Т =
 .
С учетом числовых значений
.
С учетом числовых значений
а = 2 м/с2, Т = 2 Н.
Ответ: а) а = 2 м/с2, Т = 8 Н; б) а = 2 м/с2, Т = 2 Н.
Задача 4. Три тела с массами m1, m2, m3, связанные невесомыми нерастяжимыми нитями, лежат на гладкой горизонтальной поверхности. К телу массой m1 приложена сила величиной F1, направленная вдоль плоскости, а к телу массой m3 – сила величиной F2, направленная в противоположную сторону, причем F2 > F1. Найти величину силы натяжения Т нити между телами с массами m1 и m2, величину силы натяжения Т′ нити между телами с массами m2 и m3, а также величину а ускорения тел.
Дано: m1, m2, m3, F1, F2, F2 > F1.
T − ? T′ − ? а − ?
Решение.
Рассмотрим силы, действующие на каждое тело (см. рисунок). При этом вертикальные силы из анализа исключим. Дело в том, сила трения отсутствует (поверхность гладкая), и сила реакции, направленная перпендикулярно поверхности, компенсируется силой тяжести. Следовательно, вертикальные силы на движение тел влияния не оказывают.

На первое тело действует внешняя сила F1 и сила реакции R1 нити. На второе тело действуют сила реакции R2 нити, соединяющей его с первым телом, и сила R3 реакции нити, соединяющей второе тело с третьим. На третье тело действует внешняя сила F2 и сила реакции нити R4.
Запишем второй закон Ньютона для всех грузов, учитывая только горизонтальные силы:
F1 + R1= m1a1,
R2 + R3= m2a2,
F2 + R4= m1a3.
Проектируем эти уравнения на выбранную (см. рисунок) ось Х. После нахождения проекций, будем иметь:
− F1 + R1= m1a1,
− R2 + R3= m2a2,
F2 − R4= m1a3.
Поскольку нить невесома, то, с учетом третьего закона Ньютона, R1 = R2 = Т. Аналогично, R3 = R4 = Т′. Так как нить нерастяжима, то а1 = а2 = а3 = а. Тогда
− F1 + Т= m1a,
− Т + Т′= m2a,
F2 − Т′= m1a.
Имеем систему трех уравнений с тремя неизвестными (Т, Т′, а). Решая ее, получим:
Т
=
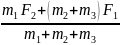 ,
Т′=
,
Т′=
 ,
а =
,
а =
 .
.
Эти выражения и являются ответом задачи.
Задача 5. К концам однородного стержня приложены две противоположно направленные силы, модули которых: F1 = 40H и F2 = 100 H. Найти величину Т силы натяжения стержня в поперечном сечении, которое делит стержень на две части в отношении 1 : 2.
Дано: F1 = 40H, F2 = 100 H, L1/L2 = 1/2.
T − ?
Решение.
Запишем второй закон Ньютона в проекциях на горизонтальную ось Х (направление оси показано на рисунке): F1x + F2x = max. После нахождения проекций, будем иметь: F2 − F1 = ma. При нахождении проекций было учтено, что ускорение направлено в сторону большей силы, что очевидно.
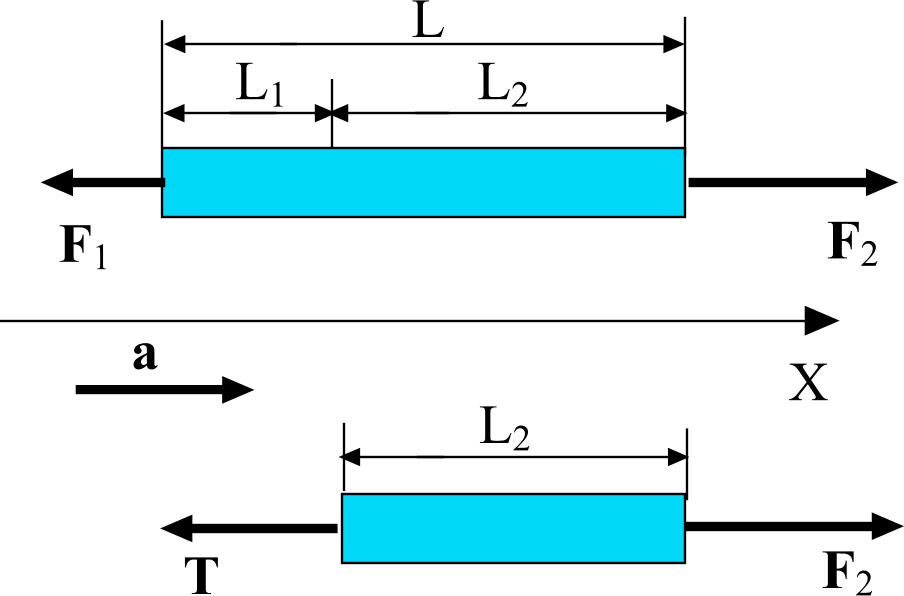
Рис. а (вверху) и Рис. b (внизу)
Если
бы модули F1
и F2
были равны между собой, стержень находился
бы в покое, и сила натяжения была бы
одинаковой в любом вертикальном сечении
стержня. Но так как модули приложенных
к стержню горизонтальных сил не равны
друг другу, стержень движется с ускорением,
величина которого а =
 .
.
При
ускоренном движении сила натяжения в
разных сечениях стержня будет различной.
Для нахождения этой силы обычно
применяется следующий прием: рассекают
стержень на две части в интересующем
сечении (рисунок а) и отбрасывают одну
из частей, например, левую. Чтобы это не
повлияло на состояние оставшейся правой
части, заменяют действие левой части
на правую введением силы натяжения Т
(рисунок b).
В результате действия разности модулей
сил F2
– T
оставшаяся правая часть стержня массой
m1
должна двигаться с ускорением, модуль
которого а =
 .
.
Это ускорение равно по величине и направлению прежнему ускорению.
Разберемся
с массой m2
оставшейся правой части стержня. По
условию задачи
=
или
 =
.
Отсюда легко найти, что L2
=
=
.
Отсюда легко найти, что L2
=
 L.
L.
Так
как стержень однородный, то масса любого
участка пропорциональна его длине.
Тогда m2
=
m.
Следовательно, а =
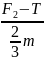 .
Тогда
=
.
.
Тогда
=
.
Из
этого уравнения находим величину силы
натяжения стержня в заданном сечении:
Т =
 .
С учетом числовых значений Т = 60 Н.
.
С учетом числовых значений Т = 60 Н.
Ответ: Т = 60 Н.
Задача 6. Тело равномерно скользит по наклонной плоскости с углом наклона α = 600. Найти коэффициент трения k тела о плоскость.
Дано: α = 600.
k − ?
Решение.
Определим силы, действующие на тело.
Тело взаимодействует с двумя объектами: с Землей и наклонной плоскостью, которая является связью. Поэтому на него будут действовать только две силы. Сила, действующая со стороны Земли – это сила тяжести Fт = mg. Сила, действующая со стороны плоскости – это сила реакции R.
Раскладываем силу реакции на две составляющие, одна из которых перпендикулярна наклонной плоскости, а другая направлена в сторону, противоположную движению тела. Первая составляющая – это сила нормальной реакции N плоскости, а вторая – сила трения Fтр.
Записываем второй закон Ньютона для тела: mg + R = ma. Ускорение при равномерном движении равно нулю, поэтому mg + R = 0. Поскольку R = N + Fтр, то mg + N + Fтр = 0. Силы, действующие на тело, располагаются в плоскости, поэтому проектировать последнее уравнение следует на две оси. Пусть направление осей такое, как показано на рисунке.

mgx + Nx + Fтр x = 0,
mgy + Ny + Fтр y = 0.
Находим проекции:
gx = g Cos (900 – α) = g Sin α, Nx = 0, Fтр x = − Fтр, gy = g Cos (1800 – α) = − g Cos α, Ny = N, Fтр y = 0. Тогда
mg Sin α − Fтр = 0, (1)
− mg Cos α + N = 0. Отсюда N = mg Cos α.
Но Fтр = kN, тогда Fтр = kmg Cos α. Подставив это выражение в (1), получим:
mg Sin α − kmg Cos α = 0, откуда k = tg α. k = tg 600 = 1,7.
Ответ: k = 1,7.
Задача 7. Два тела с массами m1 = 2 кг и m2 = 1 кг соединены упругой невесомой нитью, перекинутой через невесомый блок. Найти величину а ускорения, с которым движутся тела, и величину Т силы натяжения нити. Весом блока и трением в нем пренебречь.
Дано: m1 = 2 кг, m2 = 1 кг.
а − ? Т − ?
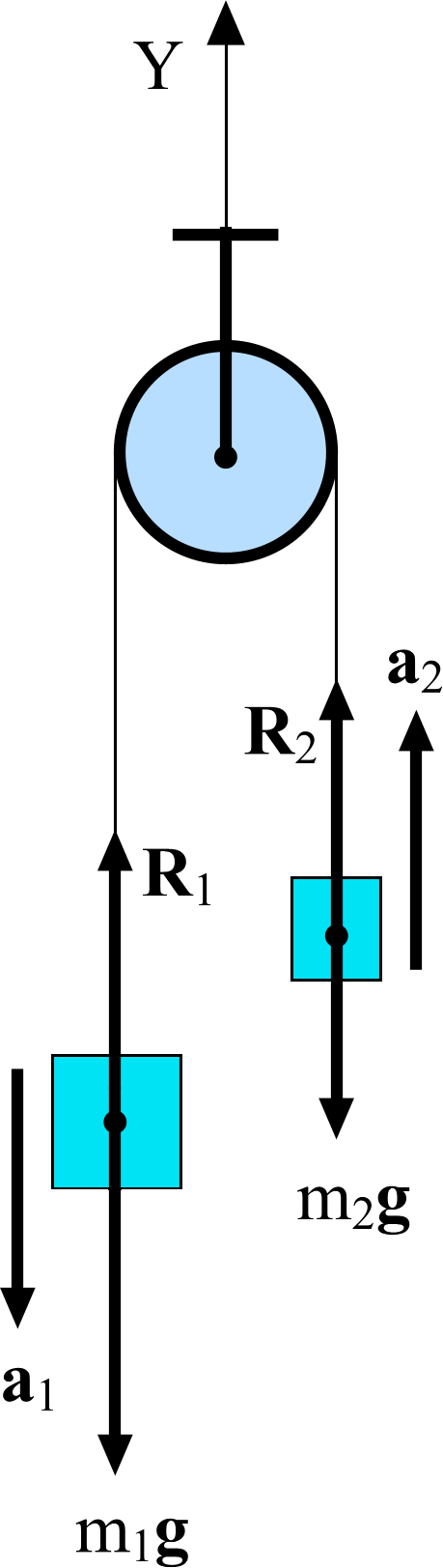
Решение.
Определим силы, действующие на каждое тело.
Первое тело взаимодействует с двумя объектами: с Землей и нитью, которая является связью. Поэтому на него будут действовать две силы. Сила, действующая со стороны Земли – это сила тяжести m1g. Сила, действующая со стороны нити – это сила реакции R1.
Аналогично, на второе тело действуют силы m2g и R2 (см. рисунок).
Записываем второй закон Ньютона для каждого тела:
m1g + R1 = ma1, m2g + R2 = ma2.
Проектируем эти уравнения на ось Y, и после нахождения проекций получим:
− m1g + R1 = − m1a1,
− m2g + R2 = m2a2.
По третьему закону Ньютона величина силы, с которой нить действует на тело с массой m1 (величина R1 силы реакции) равна величине силы, с которой это тело действует на нить (это – величина Т1 силы натяжения нити), то есть R1 = Т1. Аналогично, R2 = Т2. Тогда предыдущие уравнения примут вид:
− m1g + Т1 = − m1a1,
− m2g + Т2 = m2a2.
Имеем два уравнения с четырьмя неизвестными (Т1, a1, Т2, a2). Учитывая, что
a1 = a2 = а, Т1 = Т2 = Т, получим систему из двух уравнений с двумя неизвестными:
− m1g + Т = − m1a,
− m2g + Т = m2a. Решаем систему и находим:
a
=
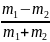 g,
Т =
g,
Т =
 g.
Подставив числа, получим:
g.
Подставив числа, получим:
а = 3,3 м/с2, Т = 13,3 Н.
Ответ: а = 3,3 м/с2, Т = 13,3 Н.
Задача 8. Невесомый блок укреплен на конце стола. Гири с массами m1 = m2 = 1 кг соединены невесомой нерастяжимой нитью и перекинуты через блок. Коэффициент трения гири массой m2 о стол k = 0,1. Найти величину а ускорения, с которым движутся гири, и величину Т силы натяжения нити. Весом блока и трением в нем пренебречь.
Дано: m1 = m2 = 1 кг, k = 0,1.
а − ? Т − ?
Решение.
Определим силы, действующие на каждую гирю.
На первую гирю массой m1 действует сила со стороны Земли – это сила тяжести m1g и сила, со стороны нити – это сила реакции нити R1.
На вторую гирю массой m2 действует сила со стороны Земли – это сила тяжести m2g, сила реакции R1 нити, и сила реакции R2 стола. Эту последнюю силу для упрощения рисунка изображать не будем, а сразу нарисуем ее компоненты: силу нормальной реакции N плоскости и силу трения Fтр, направленную против движения тела (см. рисунок).
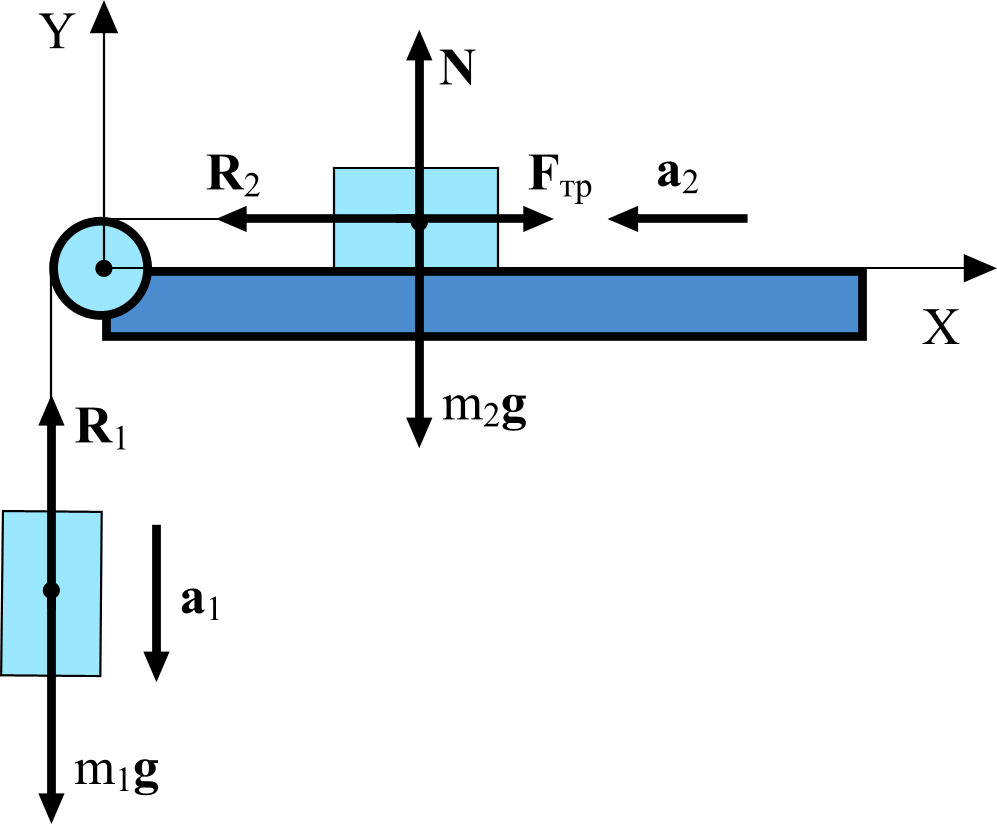
Записываем второй закон Ньютона для каждого тела сразу в проекциях на координатные оси, направления которых показаны на рисунке. При этом учтем, что проектирование для первого тела следует выполнять только на вертикальную ось, поскольку m1g, R1 и а1 направлены вдоль этой оси, и их проекции на горизонтальную ось равны нулю.
m1gy + R1y = m1a1y,
m2gx + R2x + Fтрx + Nx = m2a2x,
m2gy + R2y + Fтрy + Ny = m2a2y.
После нахождения проекций записанные уравнения примут вид:
− m1g + R1 = − m1a1,
− R2 + Fтр = − m2a2,
− m2g + N = 0.
Учитывая, что R1 = R2 = Т, a1 = a2 = а, будем иметь:
− m1g + Т = − m1a, (1)
− Т + Fтр = − m2a, (2)
N = m2g. (3)
Так как Fтр = kN, то, учитывая (3), Fтр = k m2g.
Тогда уравнение (2) будет выглядеть так: Т − km2g = m2a, откуда
Т = km2g + m2a. (4).
Подставив
это выражение для Т в (1), найдем: а =
 g.
С учетом этого выражения найдем Т из
(4):
g.
С учетом этого выражения найдем Т из
(4):
Т
=
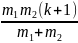 g.
С учетом числовых значенй: а = 4,5 м/с2,
Т = 5,5 Н.
g.
С учетом числовых значенй: а = 4,5 м/с2,
Т = 5,5 Н.
Ответ: а = 4,5 м/с2, Т = 5,5 Н.
Задача 9. Невесомый блок укреплен на вершине наклонной плоскости, образующей с горизонтом угол α = 300. Гири с массами m1 = m2 = 1 кг соединены невесомой нерастяжимой нитью и перекинуты через блок. Коэффициент трения гири с массой m2 о плоскость k = 0,1. Найти величину а ускорения, с которым движутся гири, и величину Т силы натяжения нити. Весом блока и трением в нем пренебречь.
Дано: m1 = m2 = 1 кг, k = 0,1.
а − ? Т − ?
Решение.
Определим силы, действующие на каждую гирю.
На первую гирю (с массой m1) действует сила со стороны Земли – это сила тяжести m1g и сила, со стороны нити – это сила реакции нити R1.
На вторую гирю действует сила со стороны Земли – это сила тяжести m2g, сила реакции R2 нити, и сила реакции стола. Эту последнюю силу для упрощения рисунка изображать не будем, а сразу нарисуем ее компоненты: силу нормальной реакции плоскости N и силу трения Fтр, направленную против движения тела (см. рисунок).

В общем случае вопрос о том, в какую сторону движутся тела, заранее определить трудно, поскольку это зависит и от соотношения масс тел, и от величины коэффициента трения тела о плоскость, и от угла наклона плоскости. Поэтому в таких случаях направление движения тел выбирается произвольно, и задача решается с учетом выбранного направления. Если в результате решения окажется, что модуль ускорения отрицателен, то это скажет о том, что направление выбрано неверно, на самом деле тела движутся в противоположную сторону.
Записываем второй закон Ньютона для каждого тела в проекциях на выбранные оси (направления осей показаны на рисунке).
m1gх + R1х = m1a1х,
m1gy + R1y = m1a1y,
m2gx + R2x + Fтрx + Nx = m2a2x,
m2gy + R2y + Fтрy + Ny = m2a2y.
Вообще-то в решении этой задачи самое сложное – это нахождение проекций. Если проекции найдены правильно, то дальше все просто. Если Вы владеете основами векторной алгебры, помните формулы приведения и изучили решения предыдущих кинематических и динамических задач, то никаких трудностей при нахождении проекций возникнуть не должно. Итак, после того, как будут найдены все 14 проекций, у Вас должно получиться следующее:
m1g Sin α − R1 Sin α = m1a1 Sin α,
− m1g Cos α + R1 Cos α = − m1a1 Cos α,
m2g Sin α − R2 + Fтр = − m2a2,
− m2g Cos α + N = 0.
Поскольку R1 = R2 = Т, a1 = a2 = а (смотри задачу 12.1.3), то:
m1g − Т = m1a, (1)
− m1g + Т = − m1a, (2)
m2g Sin α − Т + Fтр = − m2a, (3)
− m2g Cos α + N = 0. (4)
Легко видеть, что уравнения (1) и (2) это – одно и то же, а именно:
Т = m1g − m1a. (5)
Из (4) N = m2g Cos α. Поскольку Fтр = kN, то Fтр = km2g Cos α, и уравнение (3) примет вид:
m2g Sin α − Т + km2g Cos α = − m2a.
Подставляем в это уравнение выражение для Т из (5) и после несложных преобразований находим величину ускорения.
а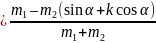 g.
g.
Тогда из (5) находим величину силы натяжения нити. После простых преобразований имеем:
Т
=
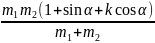 g.
g.
С учетом числовых значений а = 4 м/с2, Т = 6 Н.
Ответ: а = 4 м/с2, Т = 6 Н.
Задача 10. Невесомый блок укреплен на вершине двух наклонных плоскостей, образующих с горизонтом углы α = 300 и β = 450. Гири с массами m1 = m2 = 1 кг соединены невесомой нерастяжимой нитью и перекинуты через блок (см. рисунок). Коэффициенты трения гирь о плоскости k1 = k2 = k = 0,1. Найти величину а ускорения, с которым движутся гири, и величину Т силы натяжения нити. Весом блока и трением в нем пренебречь. Показать, что из формул, дающих решение этой задачи, можно получить, как частные случаи, решения задач 12.1.7 – 12.1.9.
Дано: m1 = m2 = 1 кг, k1 = k2 = k = 0,1.
а − ? Т − ?
Решение.
Определим силы, действующие на каждую гирю.
На первую гирю действуют следующие силы: m1g – сила тяжести со стороны Земли,
N1 – сила нормальной реакции плоскости, Fтр1 – сила трения, R1 – сила реакции нити.
На вторую гирю действуют следующие силы:
m2g – сила тяжести со стороны Земли, N2 – сила нормальной реакции плоскости, Fтр2 – сила трения, R1 – сила реакции нити.
Предположим, что гири движутся в направлениях, указанных на рисунке.
Записываем второй закон Ньютона для каждой гири в проекциях на выбранные оси. Оси для каждой гири – свои, так будет легче искать проекции. Направления осей показаны на рисунке.
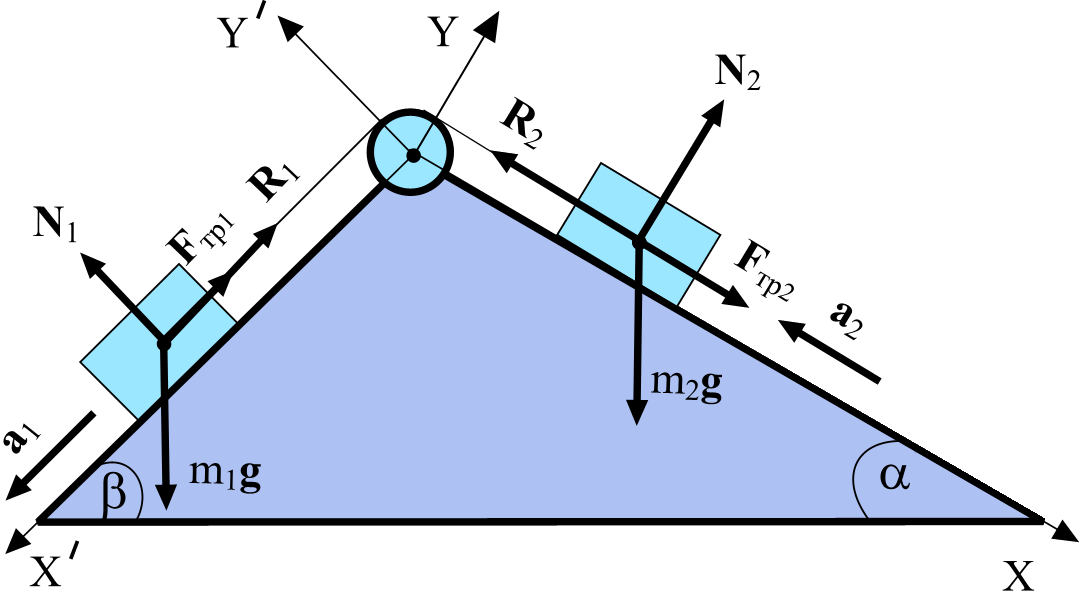
m1gx′ + R1x′ + Fтр1x′ + N1x′ = m1a1x′,
m1gy′ + R1y′ + Fтр1y′ + N1y′ = m1a1y′,
m2gx + R2x + Fтр2x + N2x = m2a2x,
m2gy + R2y + Fтр2y + N2y = m2a2y.
После того, как будут найдены все 20 проекций, у Вас должно получиться следующее:
m1g Sin β− R1 − Fтр1 = m1a1,
− m1g Cos β + N1 = 0,
m2g Sin α − R2 + Fтр2 = − m2a2,
− m2g Cos α + N2 = 0.
Поскольку R1 = R2 = Т, a1 = a2 = а (смотри задачу 12.1.3), то:
m1g Sin β− Т − Fтр1 = m1a, (1)
− m1g Cos β + N1 = 0, (2)
m2g Sin α − Т + Fтр2 = − m2a, (3)
− m2g Cos α + N2 = 0. (4)
Из (2) N1 = m1g Cos β. Поскольку Fтр1 = kN1, то
Fтр1 = km1g Cos β, и уравнение (1) примет вид:
m1g Sin β− Т − km1g Cos β = m1a. (5)
Аналогично, из (4) N2 = m2g Cos α. Поскольку Fтр2 = kN2, то Fтр2 = km2g Cos α, и уравнение (3) примет вид:
m2g Sin α − Т + km2g Cos α = − m2a. (6)
Решая совместно уравнения (5) и (6), найдем а и Т. В результате решения получим:
а
=
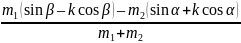 g,
g,
T
=
 g.
g.
Подставив числа, получим: а = 0,2 м/с2, Т = 6 Н.
Чтобы показать, что из формул, дающих решение этой задачи, можно получить как частные случаи решения задач 12.1.7 – 12.1.9, надо в конечных формулах данной задачи положить: α = 900, β = 900 (для задачи 12.1.7); α = 00, β = 900 (для задачи 2.1.8); β = 900 (для задачи 2.1.9).
Ответ: а = 0,2 м/с2, Т = 6 Н.
Задача 11. К оси подвижного блока прикреплен груз массой m. С какой по величине силой F нужно тянуть конец невесомой нерастяжимой нити, перекинутой через второй неподвижный блок, чтобы груз двигался вверх: 1) с ускорением, величина которого равна а; 2) чтобы груз покоился? Массами блоков и трением в них пренебречь.
Дано: m, а.
F − ?
Решение.
Рассмотрим силы, действующие на подвижный блок и груз.
Подвижный блок взаимодействует с двумя ветвями нити, идущими вверх от блока, и с нитью, идущей от центра блока вниз к грузу. Нити являются связями, поэтому на подвижный блок будут действовать силы реакций 2R1 (R1 + R1 от верхних ветвей) и R2 (от нити, идущей к грузу). Груз взаимодействует с Землей и нитью, поэтому на него действуют: mg – сила тяжести со стороны Земли и R3 – сила реакции нити.
Записываем второй закон Ньютона для подвижного блока и груза в проекциях на ось Y (см. рисунок).

При этом учтем, что масса блока по условию задачи равна нулю.
2R1y + R2y= 0,
mgy + R3y = may.
После нахождения проекций, получим:
2R1 − R2 = 0,
− mg + R3 = ma.
Поскольку R2 = R3, R1 = F (смотри задачу 12.1.3), то:
2F − R2 = 0,
− mg + R2 = ma.
Решая
эту систему уравнений, получим: F
=
 .
.
Если
груз покоится, то а = 0, тогда F
=
 .
.
Ответ: 1) F = ; 2) F = .
Задача 12. Определить величину ускорения грузов с массами m1, m2, m3, а также натяжения нитей в системе, изображенной на рисунке, если m1 = 8 кг, m2 = 6 кг, m3 = 2 кг. Нити считать невесомыми и нерастяжимыми. Массами блоков и трением в них пренебречь.
Дано: m1 = 8 кг, m2 = 6 кг, m3 = 2 кг.
а1 − ? а2 − ? а3 − ? Т1 − ? Т2 − ? Т3 − ?
Решение.
В общем случае (то есть при произвольных массах грузов) заранее трудно знать направления движения грузов и подвижного блока, поэтому предположим, что эти направления таковы, как показано на рисунке (при данных в условии задачи массах это похоже на правду).
Рассмотрим силы, действующие на грузы и подвижный блок.
Груз с массой m1 взаимодействует с Землей и нитью, поэтому на него действуют: m1g – сила тяжести со стороны Земли и R1 – сила реакции нити. Аналогично, на груз с массой m2 действуют силы m2g и R2, а на груз с массой m3 действуют силы m3g и R3.
Подвижный блок взаимодействует с двумя ветвями нити, идущими вниз от блока (силы реакций F2 и F3), и с нитью, идущей от центра блока вверх к неподвижному блоку (сила реакции F1).
Записываем второй закон Ньютона для грузов и подвижного блока в проекциях на ось Y (см. рисунок). При этом учтем, что масса блока по условию задачи равна нулю.
m 1gy
+ R1y
= m1a1y,
1gy
+ R1y
= m1a1y,
m2gy + R2y = m2a2y,
m3gy + R3y = m3a3y,
F1y + F2y + F3y = 0. После нахождения проекций, получим:
m1g − R1 = m1a1,
m2g − R2 = m2a2,
m3g − R3 = − m3a3,
− F1 + F2 + F3 = 0.
Учтем, что R1 = F1 = Т1, где Т1 – сила натяжения верхней нити; R2 = R3 = Т2 =Т3, где Т2 – сила натяжения той ветви нити, к которой прикреплен груз с массой m2, Т3 – сила натяжения той ветви нити, к которой прикреплен груз с массой m3;
F2 + F3 = R2 + R3 = Т3 + Т2 = 2Т2 (смотри задачу 12.1.3). Тогда
m1g − Т1 = m1a1, (1)
m2g − Т2 = m2a2, (2)
m3g – Т2 = − m3a3. (3)
− Т1
+ 2Т2
= 0 или Т2
=
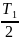 .
Подставим это выражение для Т2
в (2) и (3). Кроме того, m1,
m2,
m3,
g
заменим их числовыми значениями, что
заметно упростит решение. В результате
будем иметь:
.
Подставим это выражение для Т2
в (2) и (3). Кроме того, m1,
m2,
m3,
g
заменим их числовыми значениями, что
заметно упростит решение. В результате
будем иметь:
80 − Т1 = 8a1,
60 − = 6a2,
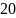 –
=
− 2a3.
–
=
− 2a3.
Мы получили три уравнения с четырьмя неизвестными (Т1, а1, а2, а3). Очевидно, что необходимое для решения системы четвертое уравнение должно выражать связь между а1, а2, а3. В общем-то, в нахождении этой связи и состоит основная трудность решения данной задачи.
Скорее всего, в этом вопросе нам поможет кинематика. Обратим внимание на то, что все три ускорения представлены в неподвижной системе отсчета Земли (или неподвижного блока). При этом ускорения а2 и а3 будут связаны с ускорениями соответствующих тел в движущейся системе отсчета (связанной с подвижным блоком) кинематическим законом сложения ускорений. Если обозначить ускорения тел с массами m2 и m3 в подвижной системе отсчета как а2от и а3от соответственно, а ускорение самой подвижной системы как апер, то а2 = а2от + апер, а3 = а3от + апер. Спроектировав эти последние два уравнения на ось Y, предположив, что апер направлено вверх, и, найдя проекции, получим:
а2 = а2от − апер, − а3 = − а3от − апер. В то же время, апер, то есть величина ускорения подвижного блока равна а1 (по причине нерастяжимости нити).
Тогда а2 = а2от − апер, − а3 = − а3от − апер. Кроме того, а2от = а3от (по той же причине). Пусть а2от = а3от = = аот. Тогда закон сложения ускорений будет выглядеть так:
а2 = аот – а1, − а3 = − аот – а1.
Сложив
последние два уравнения, будем иметь:
а2
− а3
= − 2а1
или а1
=
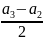 .
.
Вот мы и получили недостающее четвертое уравнение. Тогда:
80 − Т1 = 4(а3 – а2), (4)
120 − Т1 = 12a2, (5)
40 – Т1 = − 4a3. (6)
Решим полученную систему уравнений. Вычтем (6) из (5):
80 = 12a2 + 4a3. Выразим отсюда a2 и подставим в (4):
a2
=
 .
Тогда (4) примет вид: 80 − Т1
= 4
.
Тогда (4) примет вид: 80 − Т1
= 4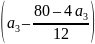 .
Решив это уравнение относительно Т1,
получим: Т1
=
.
Решив это уравнение относительно Т1,
получим: Т1
=
 .
Подставим это выражение в (6) и решим
полученное уравнение относительно a3.
В результате получим: a3
≈ 7 м/с2.
Тогда Т1
≈ 69 Н. Поскольку Т2
= Т3
=
,
то Т2
= Т3
≈ 35 Н.
.
Подставим это выражение в (6) и решим
полученное уравнение относительно a3.
В результате получим: a3
≈ 7 м/с2.
Тогда Т1
≈ 69 Н. Поскольку Т2
= Т3
=
,
то Т2
= Т3
≈ 35 Н.
Подставив
числовое значение a3,
в выражение для a2,
найдем: a2
≈ 4 м/с2.
Ранее мы нашли, что а1
=
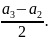 С учетом числовых значений а1
≈ 1,5 м/с2.
С учетом числовых значений а1
≈ 1,5 м/с2.
В заключение надо заметить, что направления движения и грузов и подвижного блока мы выбрали произвольно и даже угадали (что было нетрудно при данных в задаче числовых значениях). Однако при других конкретных значениях m1, m2, m3 некоторые объекты могут двигаться совсем не в ту сторону, как предположили мы, а в прямо противоположную. В этом случае какой-то из найденных модулей векторных величин примет отрицательное значение. А поскольку модуль вектора должен быть всегда только положительной величиной, то по возникшему минусу мы сможем сделать вывод о том, где мы ошиблись с направлением.
Ответ: а1 ≈ 1,5 м/с2, a2 ≈ 4 м/с2, a3 ≈ 7 м/с2, Т1 ≈ 69 Н, Т2 = Т3 ≈ 35 Н.
Задача 13. Через два неподвижных блока перекинута невесомая и нерастяжимая нить, к концам которой подвешены грузы. Масса первого груза m1, масса второго груза m2. Нить между блоками разрезали и присоединили к динамометру (см. рисунок). Что покажет динамометр, если m1 = m2 = m = 3 кг? Что покажет динамометр, если массу второго груза уменьшить на Δm1 = 1 кг? На какую величину Δm2 надо увеличить массу первого груза, чтобы динамометр вернулся к прежнему показанию? Массами блоков и трением в них пренебречь.
Дано: m1 = m2 = m = 3 кг, Δm1 = 1 кг.
Т1 − ? Т2 − ? Δm2 − ?
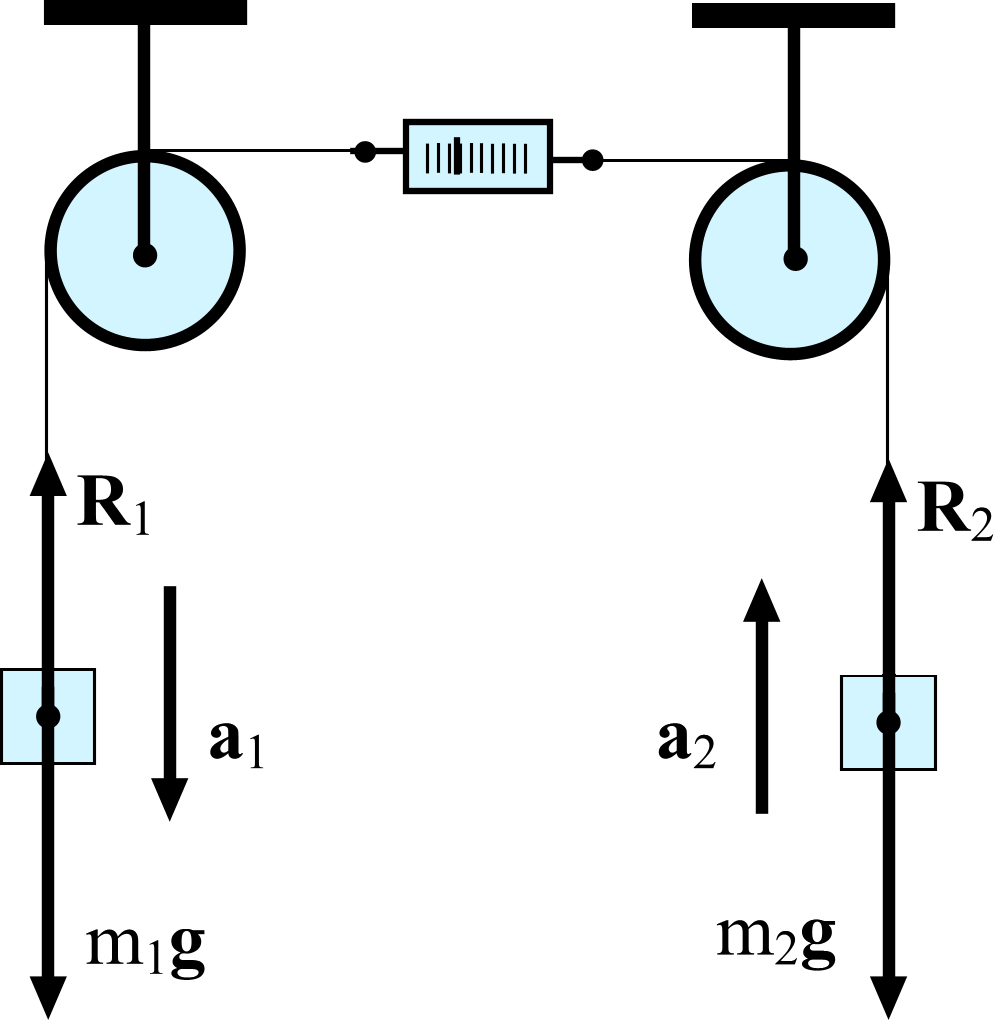
Решение.
При решении этой задачи следует иметь в виду, что динамометр показывает величину силы натяжения нити.
Пожалуй, уже не следует подробно рассматривать силы, действующие на грузы и очередной раз отправлять Вас к решению задачи 12.1.3, поскольку Вы уже накопили приличный опыт решения задач и, надеюсь, не будете возражать, если я сразу напишу:
m1g − Т = m1a, (1)
m2g − Т = m2a, (2)
где Т – величина силы натяжения нити, а – величина ускорения грузов.
Решим эту систему уравнений относительно Т. Для этого, например, выразим а из первого уравнения и полученное выражение подставим во второе. После простых преобразований Вы должны получить: Т = g.
Это – общее выражение для силы натяжения нити, то есть для любых значений m1 и m2. Перейдем к частным случаям.
Пусть
m1
= m2
= m.
Тогда Т = Т1
=
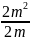 g
= mg.
g
= mg.
Так как по условию задачи m = 3 кг, то Т1 = 30 Н.
Во втором частном случае массу второго груза уменьшили на Δm1, тогда
Т
= Т2
=
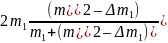 g
=
g
=
 g.
Подставив числа, получим: Т2
= 24 Н, что и покажет динамометр.
g.
Подставив числа, получим: Т2
= 24 Н, что и покажет динамометр.
И, наконец, чтобы вернуться к прежнему показанию динамометра, решили увеличить массу первого груза на Δm2, оставив при этом второй груз уменьшенным на Δm1. Тогда
Т1
=
 g,
или
g,
или
mg = g.
Решив последнее уравнение относительно Δm2, получим:
Δm2
=
 .
Подставив числа, получим: Δm2
= 3 кг.
.
Подставив числа, получим: Δm2
= 3 кг.
Ответ: Т1 = 30 Н, Т2 = 24 Н, Δm2 = 3 кг.
Задача 14. Через два неподвижных блока перекинута нить с грузами на ее концах. Масса первого груза m1, масса второго груза m2. На нити расположен подвижный блок с грузом массой m3, который соединен с подвижным блоком тоже с помощью нити (см. рисунок). Определить, с какими по величине ускорениями движутся грузы и величины сил натяжения нитей. Массами блоков и трением в них пренебречь. Нити считать невесомыми и нерастяжимыми.
Дано: m1, m2, m3.
а1 − ? а2 − ? а3 − ? Т − ? Т′ − ?
Р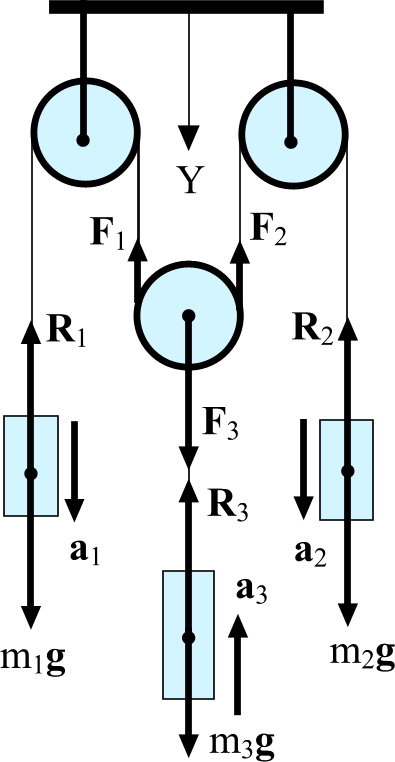 ешение.
ешение.
Заведомо мы не можем знать направления движения тел, поскольку это определяется их массами. Будем считать, что грузы с массами m1 и m2 опускаются, а груз с массой m3 поднимается, как показано на рисунке.
На рисунке также обозначены силы тяжести, действующие на грузы и силы реакции нитей, действующие на грузы и подвижный блок (m1g, m2g, m3g, R1, R2, R3, F1, F2, F3).
Запишем второй закон Ньютона для грузов и подвижного блока в проекциях на ось Y, направленную вертикально вниз (при составлении уравнения для блока не забывайте, что его массой мы пренебрегаем). Думаю, что для такого простого случая Вы легко найдете проекции сил и ускорений в уме. Итак,
m1g – R1 = m1a1
m2g – R2 = m2a2,
m3g – R3 = − m3a3,
F3 – (F1 + F2) = 0.
Поскольку нить невесома, то R1 = F1 = F2 = R2 = Т, R3 = F3 = Т′. Здесь, Т – сила натяжения нити с грузами m1 и m2 и подвижным блоком, Т′ − сила натяжения нити, соединяющей груз m3 с подвижным блоком. Тогда из последнего уравнения системы следует, что Т′ = 2Т, и первые три уравнения системы примут вид:
m1g – Т = m1a1 (1)
m2g – Т = m2a2, (2)
m3g – 2Т = − m3a3. (3)
Мы получили систему трех уравнений с четырьмя неизвестными (а1, а2, а3, Т). Для решения системы необходимо еще одно уравнение. Очевидно, это уравнение должно как-то связывать величины трех ускорений. Как найти эту связь? Наверно, в этом и заключена «изюминка» данной задачи. Все не так сложно, в этом вопросе нам помогут знания по кинематике.
Пусть
в начальный момент времени грузы, и
подвижный блок находятся в покое. Спустя
время t,
первый груз опустился на расстояние
ℓ1,
а второй – на расстояние ℓ2.
При этом подвижный блок поднимется на
расстояние ℓ3.
И вот здесь нужно сообразить, что 2ℓ3
= ℓ1
+ ℓ2.
Чтобы это понять, посмотрите внимательно
на рисунок и допустите, что блок поднялся
до уровня неподвижных блоков. Когда он
при этом прошел свое расстояние ℓ3,
то две ветви нити по обе стороны от блока
исчезнут. Причем каждая ветвь имела
длину ℓ3.
Куда подевалась часть нити длиной 2ℓ3?
Она ушла вниз на перемещения первого и
второго грузов. Вот и получается, что
2ℓ3
= ℓ1
+ ℓ2.
В то же время ℓ1
=
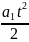 ,
ℓ2
=
,
ℓ2
=
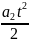 ,
ℓ3
=
,
ℓ3
=
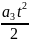 .
Тогда получается, что 2а3
= а1
+ а2.
Вот мы и нашли недостающее четвертое
уравнение. Осталось только решить
систему, состоящую из уравнений (1) –
(3) и того, что мы только что нашли. Это
«удовольствие» я предлагаю испытать
Вам самим. «Насладившись» решением, Вы
должны получить следующее:
.
Тогда получается, что 2а3
= а1
+ а2.
Вот мы и нашли недостающее четвертое
уравнение. Осталось только решить
систему, состоящую из уравнений (1) –
(3) и того, что мы только что нашли. Это
«удовольствие» я предлагаю испытать
Вам самим. «Насладившись» решением, Вы
должны получить следующее:
а1
=
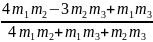 g,
g,
а2
=
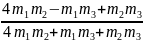 g,
g,
а3
=
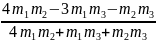 g,
g,
Т
=
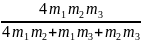 g.
g.
Учитывая,
что Т′ = 2Т, имеем: Т′ =
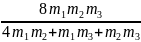 g.
g.
В какую сторону реально будут двигаться объекты с конкретными массами, мы можем узнать по знаку, который появится после подстановки чисел в формулы для ускорений.
Задача 15. К концам невесомой и нерастяжимой нити, перекинутой через невесомый и неподвижный блок, подвешены два груза массой по 100 г каждый. На один из грузов положен перегрузок массой 10 г. Найти силу, с которой перегрузок давит на груз.
Дано: m1 = m2 = 100 г, m = 10 г.
F − ?
Решение.
Рассмотрим силы, действующие на каждый из грузов и на перегрузок.
На первый груз действуют: сила тяжести m1g, сила реакции нити R1, сила давления перегрузка F.
На второй груз действуют: сила тяжести m2g и сила реакции нити R2.
На перегрузок действуют: сила тяжести mg и сила нормальной реакции N со стороны первого груза.
Н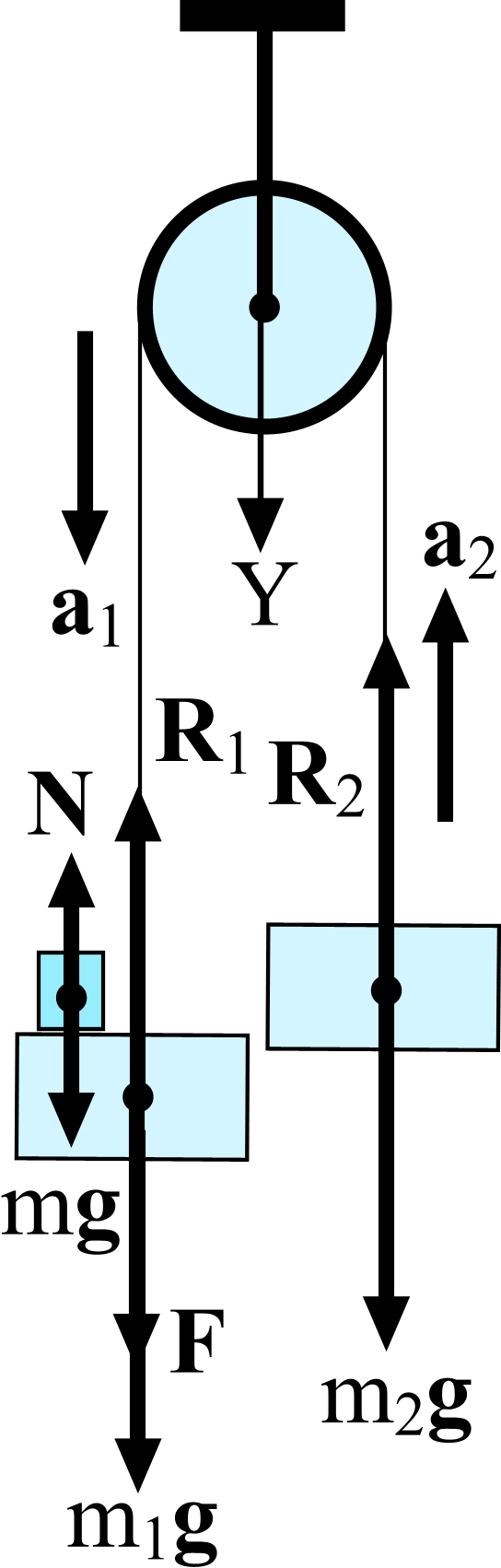 аправления
движения грузов очевидно, оно показано
на рисунке.
аправления
движения грузов очевидно, оно показано
на рисунке.
Запишем второй закон Ньютона для грузов и перегрузка в проекциях на ось Y, направленную вертикально вниз. При этом учтем, что R1 = R2 = T, а1 = а2 = а, где Т – сила натяжения нити, а – ускорение грузов и перегрузка. Итак,
m1g + F – Т = m1a, (1)
m2g – Т = − m2a, (2)
mg – N = ma. (3)
Выражаем Т из уравнения (1): Т = m1g + F − m1a. Подставляем это выражение в (2) вместо Т:
m2g – m1g −F + m1a = − m2a. Находим отсюда F:
F = m2g – m1g + m1a + m2a = m1a + m2a, поскольку m2g = m1g. Обозначим m1 + m2 как М, тогда F = Ма. Записываем это выражение вместо N в уравнении (3) на том основании, что по третьему закону Ньютона N = F: mg – Ма = ma. Из этого уравнения находим ускорение:
а
=
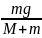 .
.
Из
(3): N
= F
= mg
– ma
= mg
– m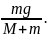 Выполнив действия, получим: F
=
Выполнив действия, получим: F
=
 .
.
С учетом числовых значений F ≈ 0,1 Н.
Ответ: F ≈ 0,1 Н.
