Уфимский Государственный Авиационный Технический Университет

Отчет к лабораторной работе № 1

«Точка в 3d пространстве»

Выполнила:

Студентка группы

МО-327

Меренкова Юлия

Уфа 2012

Содержание:

Постановка задачи…………………………………………………………………………………..3

Теория………………………………………………………………………………………………..4

Структура решения (этапы решения и их взаимосвязь)………………………………………….7

Обзор и анализ методов решений………………………………………………………………….8

Описание реализации применяемых методов…………………………………………………...11

Описание программного обеспечения (руководство программиста)………………………….12

Описание интерфейса с пользователем (руководство пользователя)………………………….15

Постановка задачи.

Формальная постановка задачи.

Написать программу, отображающую на экране пространственный макет точки А, а также комплексный чертеж этой точки. Реализовать возможность динамического изменения координат данной точки А, а также изменение угла между отрицательным направлением оси OX и положительным направлением OY.

Содержательная постановка задачи.

Экран должен содержать:

1. ортогональную систему плоскостей с изображением точки А, ее проекций А₁, А₂, А₃ и линий проекционной связи (в виде параллелепипеда);

2. комплексный чертеж с изображением проекций А₁, А₂, А₃ и линий связи;

3. ползунковые переключатели для интерактивного изменения координат (x,y,z) точки А и угла между осями OX и OY.

Динамика:

1. при изменении координат точки А должны изменяться соответствующие проекции и сама точка А на "пространственном" и комплексном чертежах;

2. при изменении угла между плоскостями OX и OY “пространственный” чертеж должен перерисовываться.

Теория.

Ортогональная система трех плоскостей проекций

В основу построения любого изображения положена операция проецирования.

Сущность метода ортогонального проецирования заключается в том, что предмет проецируется на две взаимно перпендикулярные плоскости лучами, ортогональными (перпендикулярными) к этим осям.

Одну из плоскостей проекций П₁ располагают горизонтально, а вторую П₂ - вертикально. Плоскость П₁ называют горизонтальной плоскостью проекций, П₂ - фронтальной. Плоскости П₁ и П₂ бесконечны и непрозрачны.

При построении проекций необходимо помнить, что проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость. Проекцию точки А на горизонтальную плоскость называют горизонтальной проекцией и обозначают А₁, проекцию точки А на фронтальную плоскость - фронтальной проекцией и обозначают А₂. Каждая из них является основанием перпендикуляра, опущенного из данной точки А соответственно на плоскости П₁ и П₂. Две проекции точки определяют ее положение в пространстве. Так как каждая фигура или тело представляет собой совокупность точек, то можно утверждать, что две ортогональные проекции предмета (при наличии буквенных обозначений) вполне определяют его форму.

Однако в практике изображения строительных конструкций, машин и различных инженерных сооружений возникает необходимость в создании дополнительных проекций. Чтобы сделать проекционный чертеж более ясным и удобочитаемым, используют третью плоскость, перпендикулярную П₁ и П₂. Эта плоскость обозначается буквой П₃ и называется профильной.

Проекции точек на плоскость П₃ называются профильными и обозначают А₃.

Плоскости проекций, попарно пересекаясь, определяют три оси: Ox, Oy и Oz, которые можно рассматривать как систему прямоугольных декартовых координат в пространстве с началом в точке O. Система знаков, соответствующая “правой системе” координат, показана на Рис.

Три плоскости проекций делят пространство на восемь трехгранных углов - это так называемые октанты.

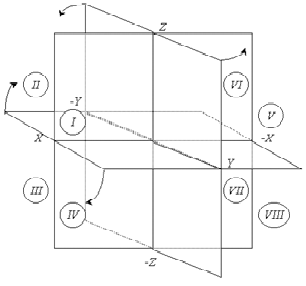
Рис. 1. – Нумерация октантов.

Рассматривая ортогональные проекции, предполагают, что наблюдатель находится в первом октанте. Проекционный чертеж, на котором плоскости проекций со всем тем, что на них изображено, совмещены определенным образом одна с другой, называется эпюром. Для получения эпюра плоскости П₁ и П₃ вращают как показано на Рис., до совмещения с плоскостью П₂. В результате вращения передняя полуплоскость П₁ оказывается совмещенной с нижней полуплоскостью П₂, а задняя полуплоскость П₁ - с верхней полуплоскостью П₂. Окончательный вид всех совмещенных плоскостей проекций дан на рисунке.

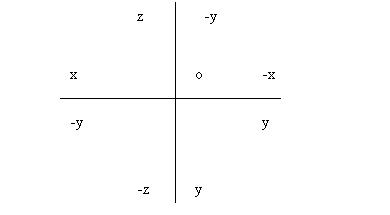
Рис. 2. – Эпюр Монжа.