5.2. Абсолютно черное тело. Закон Кирхгофа.
Е
сли
поглощательная способность тела
,
а его отражательная способность
,
то тело называется абсолютно
черным.
Абсолютно черное тело при любой
температуре полностью поглощает всю
энергию падающих на него электромагнитных
волн независимо от их частоты, поляризации
и направления распространения, ничего
не отражая и не пропуская. Испускательную
способность абсолютно черного тела
будем обозначать через
.
Она зависит только от частоты излучения
и абсолютной температуры Т
тела.
Все реальные тела не являются абсолютно черными. Однако некоторые из них в определенных интервалах частот близки по своим свойствам к абсолютно черному телу. Например, в области частот видимого света поглощательные способности сажи, платиновой черни и черного бархата мало отличаются от единицы. Наиболее совершенной моделью абсолютно черного тела может служить небольшое отверстие в непрозрачной стенке замкнутой полости (рис. 5.2.1). Луч света, попадающий внутрь полости через отверстие, претерпевает многократные отражения от стенок полости, прежде чем он выйдет из полости обратно. При каждом отражении происходит частичное поглощение энергии света стенками. Поэтому независимо от материала стенок интенсивность луча света, выходящего из полости через отверстие, во много раз меньше интенсивности падающего извне первичного пуча. Очевидно, что отверстие тем ближе по своим свойствам к абсолютно черному телу, чем больше отношение площади поверхности полости к площади отверстия. Рассмотренная модель абсолютно черного тела позволяет понять, почему узкий вход в пещеру или открытые окна домов снаружи кажутся черными, хотя внутри пещеры около входа или внутри комнат дома достаточно светло из-за отражения дневного света от стен. По той же причине шероховатые ткани с большим ворсом обладают большей поглощательной способностью, чем гладкие.
Тело,
для которого поглощательная способность
не зависит от частоты и меньше единицы
(
),
называется серым.
М
ежду
испускательной
и поглощательной
способностью любого тела существует
взаимосвязь. Ее можно установить,
проделав следующий мысленный эксперимент.
Пусть внутри замкнутой оболочки, в
которой создан высокий вакуум (для
исключения теплопроводности между
телами), стенки которой поддерживаются
при определенной температуре Т,
находится несколько разных тел
(рис. 5.2.2).
Поскольку в внутри оболочки создан высокий вакуум, то тела могут обмениваться энергией между собой и стенками полости, лишь испуская и поглощая электромагнитные волны. Опыт показывает, что такая система через некоторое время приходит в термодинамическое равновесие, и тела системы будут иметь температуру Т, равную температуре оболочки. Отсюда следует, что тело, обладающее большей испускательной способностью, должно поглощать больше энергии (правило Прево). Если какое-то тело будет больше поглощать, чем испускать, то оно будет нагреваться, если наоборот – то остывать. А это противоречит условию термодинамического равновесия. Оказывается, что для рассмотренной системы тел должно выполняться следующее соотношение:
.
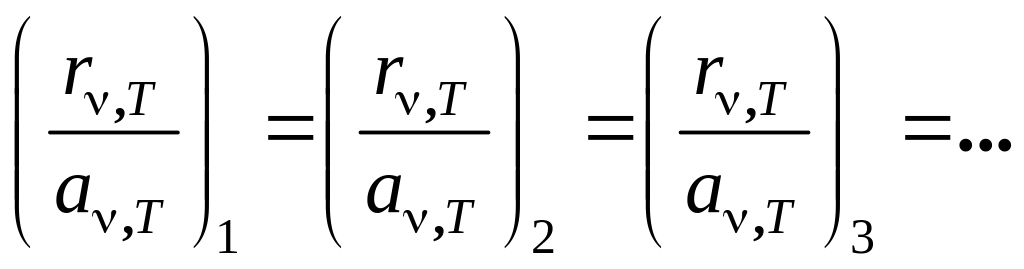(5.2.1)
Так все тела системы могут различными, то из (5.2.1) следует, что отношение испускательной способности тела к его поглощательной способности не зависит от природы тела и является универсальной функцией температуры и частоты
.
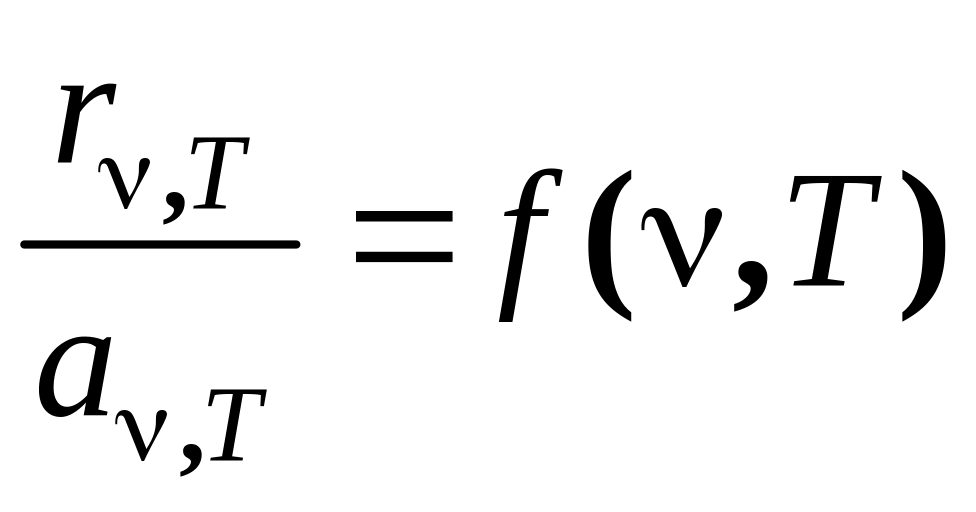(5.2.2)
Выражение
(5.2.2) получило название закон
Кирхгофа.
Этот закон теплового излучения был
установлен в 1859 г. немецким физиком
Густавом Кирхгофом. Функция
получила название универсальной
функции Кирхгофа.
Так
как поглощательная способность абсолютно
черного тела
,
то из уравнения (5.2.1) следует, что
универсальная функция Кирхгофа равна
излучательной способностью абсолютно
черного тела:
.
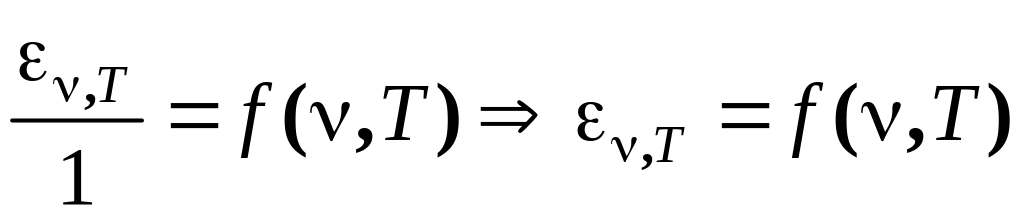(5.2.3)
С учетом выражения (5.2.3) закон Кирхгофа можно записать в виде:
,
(5.2.4)
– отношение испускательной способности тела к его поглощательной способности не зависит от материала тела и равно испускательной способности абсолютно черного тела, являющейся функцией только температуры и частоты.
Используя закон Кирхгофа и выражение (5.1.7) энергетическую светимость R любого тела можно записать в виде:
.
(5.2.5)
Если тело серое, то его энергетическая светимость равна:
.
(5.2.6)