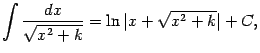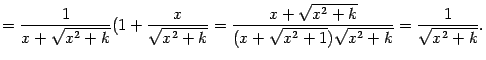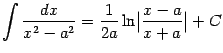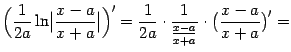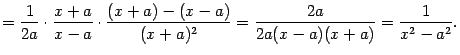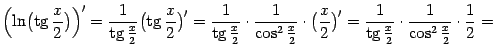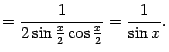- •Неопределенный интеграл
- •2. Свойства интегралов (неопределённых и определённых) Свойства неопределенного интеграла
- •Свойства определенного интеграла
- •8. Необходимое и достаточное условие интегрируемости функции
- •Интегрируемость монотонных функций
- •Интегрируемость непрерывных функций
- •9. Ормула Ньютона-Лейбница.
1.
Функция ![]() называется первообразной для
функции
называется первообразной для
функции ![]() на
промежутке
на
промежутке ![]() ,
конечном или бесконечном, если
функция
дифференцируема в
каждой точке этого промежутка и ее
производная удовлетворяет следующему
равенству:
,
конечном или бесконечном, если
функция
дифференцируема в
каждой точке этого промежутка и ее
производная удовлетворяет следующему
равенству:
![]()
Последнее равенство можно записать через дифференциалы:
![]() или
или ![]()
Пример
Функция ![]() является
первообразной для функции
является
первообразной для функции ![]() ,
так как
,
так как
![]()
Больше примеров решенийРешение интегралов онлайн
Первообразная имеет конечную производную, а, следовательно, является непрерывной функцией.
Теорема
(О бесконечном множестве первообразных для функции)
Если
функция
является
первообразной для функции
на
некотором промежутке, то и функция ![]() ,
где
,
где ![]() -
произвольная постоянная, также будет
первообразной для функции
-
произвольная постоянная, также будет
первообразной для функции![]() на
рассматриваемом промежутке.
на
рассматриваемом промежутке.
Пример
Известно,
что для функции
первообразной
является функция
,
а, следовательно, и все функции вида ![]() также
будут первообразными, так как выполняется
равенство
также
будут первообразными, так как выполняется
равенство ![]() :
:
![]()
Больше примеров решенийРешение интегралов онлайн
Таким образом, если функция имеет первообразную, то она имеет бесконечное множество первообразных.
Теорема
(Об общем виде первообразной для функции)
Если
функции
и ![]() -
две любые первообразные функции
,
то их разность равна некоторой постоянной,
то есть
-
две любые первообразные функции
,
то их разность равна некоторой постоянной,
то есть
![]()
Последнюю
теорему можно сформулировать иначе:
каждая функция, которая является
первообразной для функции
,
может быть представлена в виде ![]() .
.
Неопределенный интеграл
Определение
Совокупность
всех первообразных функции
,
определенных на заданном промежутке,
называется неопределенным
интегралом от функции
и
обозначается символом ![]() .
То есть
.
То есть
![]()
Знак ![]() называется интегралом,
называется интегралом, ![]() - подынтегральным
выражением,
- подынтегральной
функцией,
а
- подынтегральным
выражением,
- подынтегральной
функцией,
а ![]() - переменной
интегрирования.
- переменной
интегрирования.
Операция нахождения первообразной или неопределенного интеграла от функции называетсяинтегрированием функции . Интегрирование представляет собой операцию, обратнуюдифференцированию.
2. Свойства интегралов (неопределённых и определённых) Свойства неопределенного интеграла
Вычисление многих интегралов сводится к табличным, если использовать свойства неопределенных интегралов, вытекающие из соответствующих свойств дифференциалов. Рассмотрим некоторые из них:
а) Постоянный множитель можно вынести за знак неопределенного интеграла:
![]()
(1) |
Доказательство. Продифференцировав правую часть равенства, получаем:
Таким образом, дифференциал правой части доказываемой формулы равен подынтегральному выражению левой части, а это и означает справедливость формулы (1).
б) Если
существуют интегралы ![]() и
и ![]() ,
то не определенный интеграл суммы
,
то не определенный интеграл суммы ![]() равен
сумме неопределенных интегралов от
этих функций:
равен
сумме неопределенных интегралов от
этих функций:
![]()
(2) |
Доказательство. Продифференцируем правую часть равенства (2):
Мы получили подынтегральное выражение неопределенного интеграла, стоящего в левой части равенства (2), откуда и следует справедливость утверждения.

Пример
4. Вычислим
неопределенный интеграл ![]() .
.
Решение. Разделив почленно числитель на знаменатель и использовав свойство б), получаем табличные интегралы:
Замечание. Каждый
из трех неопределенных интегралов
содержит свою произвольную постоянную.
В окончательном ответе через ![]() обозначают
их сумму, которая также является
произвольной постоянной.
обозначают
их сумму, которая также является
произвольной постоянной.
Пример
5. Вычислим
интеграл от тригонометрической функции ![]() .
.
Решение. Записав
единицу, стоящую в числителе ![]() ,
в тригонометрическом виде
,
в тригонометрическом виде ![]() ,
разделим числитель почленно на
знаменатель. Применив затем свойство
б), получим:
,
разделим числитель почленно на
знаменатель. Применив затем свойство
б), получим:
Пример
6. Вычислим
интеграл от иррациональной функции ![]() .
.
Решение. Раскроем
скобки по формуле куба суммы ![]() ,
перейдем к дробным показателям, а затем
применим правила интегрирования:
,
перейдем к дробным показателям, а затем
применим правила интегрирования:
Свойства определенного интеграла
Так как определенный интеграл равен разности значений первообразной, та его свойства выводятся из свойств неопределенного интеграла.
а) Если
существует  и
и ![]() —
любое число, то
—
любое число, то  .
.
Доказательство. Из
соответствующего свойства неопределенных
интегралов следует, что если ![]() —
первообразная для
—
первообразная для ![]() ,
то
,
то ![]() —
первообразная для
—
первообразная для ![]() .
Значит,
.
Значит,
б) Если
функции ![]() и
и ![]() имеют
первообразные на отрезке
имеют
первообразные на отрезке ![]() ,
то
,
то
Доказательство. Из
соответствующего свойства неопределенных
интегралов следует, что если ![]() —
первообразная для
—
первообразная для ![]() ,
a
,
a ![]() —
первообразная для
—
первообразная для ![]() на
отрезке
,
то
на
отрезке
,
то ![]() —
первообразная для
.
Значит,
—
первообразная для
.
Значит,
в) Если
функция
имеет
первообразную на отрезке
и
если ![]() ,
то (аддитивное свойство определенного
интеграла)
,
то (аддитивное свойство определенного
интеграла)
Доказательство. Пусть — первообразная для . Тогда
Но ![]() .
Значит,
.
Значит,
что и требовалось доказать.
Доказанное свойство имеет простой геометрический смысл: оно выражает аддитивность площади криволинейной трапеции. Так, на рисунке 5
.
Тогда ![]() .
.
г) Если
функция ![]() имеет
первообразную на отрезке
,
то справедливо равенство
имеет
первообразную на отрезке
,
то справедливо равенство
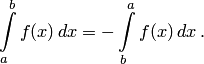
Доказательство. Пусть — первообразная для . Тогда

Но ![]() ,
откуда и следует доказываемое утверждение.
,
откуда и следует доказываемое утверждение.
д)  .
Доказательство:
.
Доказательство:  .
.
3.
Определение 1.1
Пусть ![]() --
функция, заданная на объединении
интервалов вещественной оси. Набор всех
первообразных для
называется неопределённым
интегралом от
и
обозначается
--
функция, заданная на объединении
интервалов вещественной оси. Набор всех
первообразных для
называется неопределённым
интегралом от
и
обозначается ![]() .
Операция нахождения неопределённого
интеграла по заданной
функции
называется интегрированием этой
функции; найти неопределённый интеграл
означаетпроинтегрировать данную
функцию. Функция
,
записанная после знака интеграла (или,
как часто говорят, под знаком
интеграла), называется подынтегральной
функцией.
.
Операция нахождения неопределённого
интеграла по заданной
функции
называется интегрированием этой
функции; найти неопределённый интеграл
означаетпроинтегрировать данную
функцию. Функция
,
записанная после знака интеграла (или,
как часто говорят, под знаком
интеграла), называется подынтегральной
функцией.
Согласно
доказанным выше теоремам о виде
первообразных, неопределённый интеграл
от функции
состоит
из функций вида ![]() ,
где
,
где ![]() --
какая-либо фиксированная первообразная
для
,
а
--
какая-либо фиксированная первообразная
для
,
а ![]() --
величина, постоянная на каждом из
непересекающихся интервалов, на которых
задана функция
.
Поэтому можно написать такую формулу:
--
величина, постоянная на каждом из
непересекающихся интервалов, на которых
задана функция
.
Поэтому можно написать такую формулу:
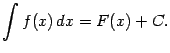
(Точнее
было бы ![]() ,
но фигурные скобки, обозначающие
множество всех функций вида
,
писать в данной ситуации не принято.)
,
но фигурные скобки, обозначающие
множество всех функций вида
,
писать в данной ситуации не принято.)
Итак,
для того чтобы доказать равенство ![]() ,
достаточно проверить, что
--
первообразная для
,
то есть что
,
достаточно проверить, что
--
первообразная для
,
то есть что ![]() .
Поэтому таблица неопределённых интегралов
для многих часто встречающихся функций
сразу следует из таблицы производных,
которую мы получили в первом семестре.
.
Поэтому таблица неопределённых интегралов
для многих часто встречающихся функций
сразу следует из таблицы производных,
которую мы получили в первом семестре.
1)
Поскольку ![]() ,
то при
,
то при ![]()
![]() и
и ![]() ,
если взять
,
если взять ![]() .
Поэтому при
.
Поэтому при ![]()
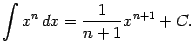
В
частности, получаем при ![]() (заметим,
что
(заметим,
что ![]() ):
):
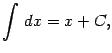
при ![]() (тогда
(тогда ![]() ):
):
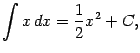
при ![]() :
:
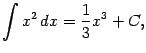
при ![]() (тогда
(тогда ![]() ):
):
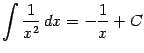
(заметим,
что здесь
--
кусочно постоянная величина, принимающая
постоянные значения ![]() при
при ![]() и
и ![]() при
при ![]() ),
при
),
при ![]() (тогда
(тогда ![]() ):
):
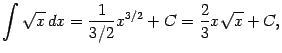
при ![]() (тогда
(тогда ![]() ):
):
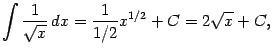
при ![]() (тогда
(тогда ![]() ):
):
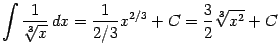
(здесь
--
кусочно постоянная, поскольку
подынтегральная функция задана на
объединении двух интервалов ![]() ),
и т. п.
),
и т. п.
2)
Пусть ![]() .
Тогда
.
Тогда ![]() не
задаётся формулой предыдущего пункта.
Однако, согласно таблице производных,
при
мы
имеем
не
задаётся формулой предыдущего пункта.
Однако, согласно таблице производных,
при
мы
имеем ![]() ,
следовательно,
,
следовательно, ![]() --
первообразная для
--
первообразная для ![]() на
интервале
на
интервале ![]() .
Проверим, что при
функция
.
Проверим, что при
функция ![]() --
первообразная для
--
первообразная для ![]() на
интервале
на
интервале ![]() .
Действительно, по правилу дифференцирования
сложной функции получаем
.
Действительно, по правилу дифференцирования
сложной функции получаем

Итак,
на объединении интервалов
)
функция ![]() служит
первообразной для
,
то есть
служит
первообразной для
,
то есть
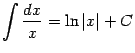
(здесь -- кусочно постоянная величина).
3)
Поскольку, согласно таблице производных,
при ![]()
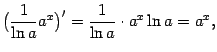
то
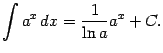
В
частности, при ![]() получаем:
получаем:
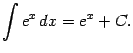
4)
Поскольку ![]() ,
получаем
,
получаем
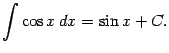
5)
Поскольку ![]() ,
получаем
,
получаем
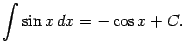
6)
Так как ![]() ,
то
,
то
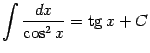
(здесь -- кусочно постоянная функция; см. пример в замечании 1.1).
7)
Аналогично, поскольку ![]() ,
получаем
,
получаем
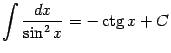
(здесь
--
кусочно постоянная функция на интервалах
вида ![]() ,
где
,
где ![]() ).
).
8)
Табличная формула ![]() означает,
что
означает,
что ![]() --
первообразная для
--
первообразная для ![]() на
интервале
на
интервале ![]() .
Значит,
.
Значит,
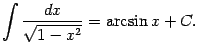
Заметим, что в соответствии с примером 1.3 мы можем также написать:

(Значения в двух последних формулах означают разные постоянные.)
Докажем
также обобщение полученной формулы:
если ![]() ,
то на интервале
,
то на интервале ![]() имеем
имеем
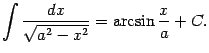
Для доказательства достаточно показать, что производная правой части равна подынтегральной функции:
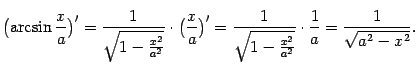
Разумеется, верна и формула
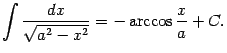
9)
Из табличной формулы ![]() (при
(при ![]() )
получаем, что
)
получаем, что
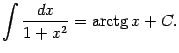
Поскольку ![]() при
любом
при
любом ![]() ,
то функция
,
то функция ![]() так
же, как и
так
же, как и ![]() ,
служит первообразной для
,
служит первообразной для ![]() .
Значит, мы можем также написать
.
Значит, мы можем также написать
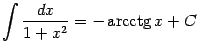
(с другим, однако, значением постоянной , нежели в предыдущей формуле).
Докажем также следующее обобщение полученной формулы: если , то
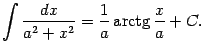
Для доказательства найдём производную правой части:
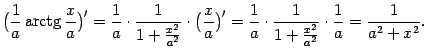
Получили подынтегральную функцию, что и доказывает формулу.
Ясно, что имеет место также формула
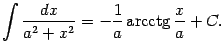
10) Докажем формулу
|
(1.1) |
где ![]() --
произвольное постоянное число. (Заметим,
что при
--
произвольное постоянное число. (Заметим,
что при ![]() формула
имеет смысл для всех
формула
имеет смысл для всех ![]() ,
а при
,
а при ![]() --
для
--
для ![]() ,
так что во втором случае величина
--
кусочно постоянная.) Для доказательства
надо рассмотреть два случая:
,
так что во втором случае величина
--
кусочно постоянная.) Для доказательства
надо рассмотреть два случая: ![]() (при
возможен
только этот случай; это неравенство
имеет место также при
и
(при
возможен
только этот случай; это неравенство
имеет место также при
и ![]() )
и
)
и ![]() (при
и
(при
и ![]() ;
поскольку
,
случай равенства нулю невозможен). В
первом случае имеем:
;
поскольку
,
случай равенства нулю невозможен). В
первом случае имеем:
|
|
|
|
|
|
Поскольку
получили подынтегральную функцию,
формула в этом случае доказана. Второй
случай, когда ![]() ,
рассматривается аналогично.
,
рассматривается аналогично.
Заметим, что функцию в правой части формулы (1.1) часто называют кдлинным логарифмом", в отличие от правой части формулы следующего пункта, тоже содержащей логарифм.
11)
Пусть
и ![]() ,
то есть
,
то есть ![]() .
Тогда
.
Тогда
|
(1.2) |
(здесь -- кусочно постоянная величина, которая на трёх интервалах изменения может принимать три разных значения).
Рассмотрим
два случая: ![]() (это
неравенство выполняется при
(это
неравенство выполняется при ![]() )
и
)
и ![]() (это
неравенство выполняется при
(это
неравенство выполняется при ![]() ).
В первом случае имеем
).
В первом случае имеем
|
|
|
|
Получили подынтегральную функцию, так что формула (1.2) в этом случае доказана. Случай рассматривается аналогично.
Функцию, стоящую в правой части формулы (1.2), часто называют квысоким логарифмом".
12) Докажем формулу
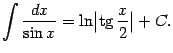
(Здесь
постоянна
на каждом из интервалов
,
,
из которых состоит область определения
подынтегральной функции ![]() .)
.)
Подсчитаем
производную правой части в случае,
когда ![]() .
Получаем:
.
Получаем:
|
|
|
|
Случай ![]() разбирается
аналогично.
разбирается
аналогично.
13) Имеет место также формула
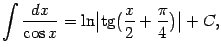
доказательство которой предоставляется читателю в качестве упражнения.
4-6. Непосредственное интегрирование[править | править викитекст]
Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. См. Таблица интегралов.
Подведение под знак дифференциала[править | править викитекст]
Данный метод эквивалентен методу замены переменной (см. далее):
![]()
Метод замены переменной (метод подстановки)[править | править викитекст]
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть
требуется вычислить интеграл ![]() Сделаем
подстановку
Сделаем
подстановку ![]() где
где ![]() —
функция, имеющая непрерывную производную.
—
функция, имеющая непрерывную производную.
Тогда ![]() и
на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой:
и
на основании свойства инвариантности
формулы интегрирования неопределенного
интеграла получаем формулу
интегрирования подстановкой:
![]()
Интегрирование
выражений вида ![]() [править | править
викитекст]
[править | править
викитекст]
Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.
Примеры[править | править викитекст]
Вычислить: ![]() Пусть
Пусть ![]() тогда
тогда ![]() и
и ![]()
Интегрирование по частям[править | править викитекст]
Основная статья: Интегрирование по частям
Интегрирование по частям — применение следующей формулы для интегрирования:
![]()
Или:
![]()
В частности, с помощью n-кратного применения этой формулы находится интеграл
![]()
где ![]() —
многочлен
—
многочлен ![]() -й
степени.
-й
степени.
Интегрирование рациональных дробей[править | править викитекст]
Основная статья: Разложение дробей при интегрировании
Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.
Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.
Всякую
правильную рациональную дробь ![]() ,
знаменатель которой разложен на множители
,
знаменатель которой разложен на множители
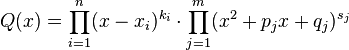
можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:
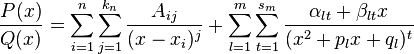
где ![]() —
некоторые действительные коэффициенты,
обычно вычисляемые с помощью метода
неопределённых коэффициентов.
—
некоторые действительные коэффициенты,
обычно вычисляемые с помощью метода
неопределённых коэффициентов.
Примеры[править | править викитекст]
Вычислить: ![]()
Разложим подынтегральное выражение на простейшие дроби:
![]()
Сгруппируем слагаемые и приравняем коэффициенты при членах с одинаковыми степенями:
![]()
![]()
Следовательно 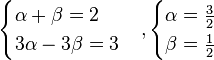
Тогда
![]()
Теперь
легко вычислить исходный интеграл ![]()
Интегрирование элементарных функций[править | править викитекст]
Основная статья: Алгоритм Риша
Для нахождения первообразной от элементарной функций в виде элементарной функции (или определения того, что первообразная не является элементарной) был разработан алгоритм Риша. Он полностью или частично реализован во многих системах компьютерной алгебры.
7. II. Задача о площади криволинейной трапеции
Рассмотрим плоскую фигуру, ограниченную линиями y = 0, x = a, x = b и y = f(x), где f(x) есть непрерывная положительная функция, заданная при a ≤ x ≤ b (см. рис. 3). Такая фигура называется криволинейной трапецией. Поставим вопрос о площади F этой трапеции.
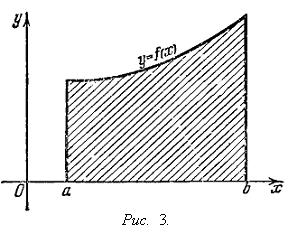
Отметим, что здесь, а отличие от двух рассмотренных выше задач, речь должна идти прежде всего о самом определении того, что такое площадь, и лишь затем - о нахождении ее численного значения. Нижеприводимое рассуждение освещает оба эти момента.
Разделим [a, b] точками a = x0 < x1 < x2 < ... < xn-1 < xn = b и пусть λ = max(xk+1 - xk). Прямые x = xk разбивают нашу трапецию на n узких полос. Так как функция f(x) непрерывна, то она мало меняется при xk ≤ x ≤ xk+1 и без большой погрешности ее можно считать на промежутке [xk, xk+1] постоянной и равной f(ξk), где ξk есть произвольно взятая точка промежутка [xk, xk+1]. Легко видеть, что сделанное допущение равносильно тому, что мы принимаем вышеупомянутые полосы за прямоугольники, а всю нашу трапецию - за ступенчатую фигуру, изображенную на рис. 4.
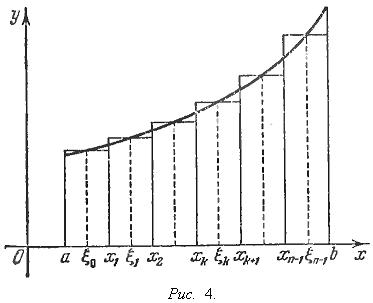
Площадь этой ступенчатой фигуры, очевидно, равна
![]()
![]()
![]()
Естественно считать, что эта площадь при малом λ является приближенным значением интересующей нас площади F. Поэтому по определению будем называть площадью нашей криволинейной трапеции предел
![]()
![]()
![]() (3)
(3)
причем, однако, здесь подлежит доказательству существование этого предела (в предыдущих двух случаях существование этого предела считали очевидным, т. к. масса m и путь s - это заведомо существующие физические величины).
Сравнивая выражения (1), (2) и (3), полученные в процессе решения рассмотренных задач, замечаем, что с чисто аналитической точки зрения все эти выражения совершенно одинаковы. Поэтому займемся изучением этих выражений, называемых определенными интегралами, уже не интересуясь их конкретным истолкованием.
Определенный интеграл
Дадим теперь точное определение понятия определенного интеграла.
Пусть на замкнутом промежутке [a, b] задана функция f(x). Проделаем следующие операции:
1) Раздробим [a, b] на части точками
x0 = a < x1 < x2 < ... < xn-1 < xn = b,
причем наибольшую из разностей xk+1 - xk обозначим через λ.
2) В каждом частичном промежутке [xk, xk+1] выберем по точке ξk и вычислим f(ξk).
3) Умножим f(ξk) на длину (xk+1 - xk) соответствующего промежутка [xk, xk+1].
4) Сложим все найденные произведения. Сумму
![]()
![]()
![]()
будем называть интегральной суммой.
5) Будем изменять произведённое дробление [a, b] так, чтобы величина λ стремилась к нулю.
Если при этом существует конечный предел
![]()
![]() (4)
(4)
не зависящий от выбора точек ξk, то этот предел называется определенным интегралом от функции f(x) по промежутку [a, b] и обозначается через
![]()
![]()
Точный смысл соотношения (4) таков: всякому ε > 0 отвечает такое δ > 0, что при любом способе дробления, у которого λ < δ, будет
| σ - I | < ε,
как
бы при этом ни были выбраны точки ![]()
![]() .
.
Предельное соотношение (4) имеет довольно своеобразный характер.
Отдадим себе отчет в том, для каких функций введенное понятие оказывается достаточно естественным.
Если у функции f(x) существует интеграл (в этом случае говорят, что f(x) интегрируема), то это означает, что суммы σ, отвечающие дроблениям с достаточно малым λ, будут близки к некоторому постоянному числу, как бы ни выбирать точки ξk. Поэтому, меняя точки ξk, не будем существенно изменять величины суммы σ. Но это возможно лишь за счет того, что изменение точек ξk не вызывает заметного изменения чиселf(ξk) (по крайней мере в большинстве слагаемых суммы σ). Для функций непрерывных указанное обстоятельство и в самом деле имеет место, т. к. точки ξk могут изменяться лишь в коротких промежутках [xk, xk+1], а у непрерывных функций близким значениям аргумента отвечают близкие же значения функции. Поэтому естественно ожидать, что у непрерывной функции определенный интеграл существует. Если же функция f(x) разрывна, то, вообще говоря, нет оснований ожидать у нее существования интеграла. Изложенные соображения подтверждаются следующей теоремой:
Теорема. Если функция f(x) непрерывна на [a, b], то интеграл
![]()
![]()
существует.
Доказательство этой теоремы довольно сложно, и мы предпошлем ему некоторые вспомогательные соображения.
Пусть на [a, b] задана непрерывная функция f(x). Разобъем [a, b] на части точками
a = x0 < x1 < x2 < ... < xn-1 < xn = b
и обозначим через Mk и mk наибольшее и наименьшее значения f(x) на частичном промежутке [xk, xk+1]. Суммы
![]()
![]()
![]()
![]()
называются соответственно верхней и нижней интегральными суммами (отвечающими выбранному способу дробления).