
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ»
ИНСТИТУТ УПРАВЛЕНИЯ ФИНАНСАМИ И НАЛОГОВОГО АДМИНИСТРИРОВАНИЯ
Кафедра математических методов в управлении:
Практическое задание
по дисциплине Эконометрика
вариант (тема) 15
Выполнил студент очной формы обучения
1 Курса магистратуры группы «Экономика»
Проверили:
Аксюк Светлана Андреевна – ассистент кафедры
Писарева Ольга Михайловна – к.э.н. доцент
Москва – 2014г.
Предварительный анализ данных.
Для анализа разброса переменных воспользуемся процедурой «Multiple Variable Analysis».
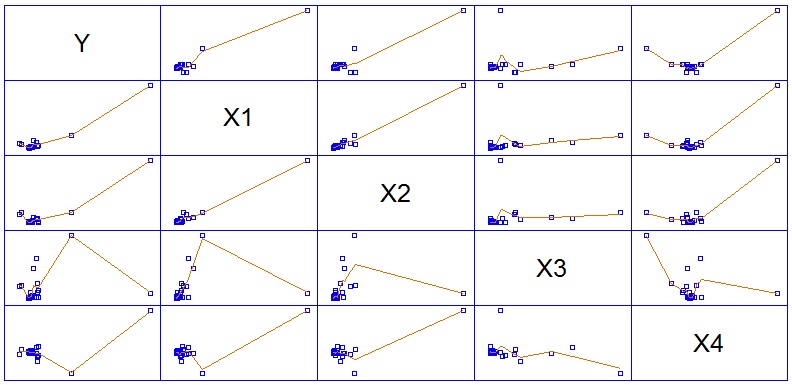
Рис. 1. Графики разброса показателей с линиями локально взвешенной регрессии до исключения аномальных наблюдений.
Таблица 1. Корреляционная матрица переменных.
|
Y |
X1 |
X2 |
X3 |
X4 |
Y |
|
0,9640 |
0,9323 |
0,2757 |
0,6647 |
|
|
(53) |
(53) |
(53) |
(53) |
|
|
0,0000 |
0,0000 |
0,0457 |
0,0000 |
X1 |
0,9640 |
|
0,9873 |
0,2419 |
0,7638 |
|
(53) |
|
(53) |
(53) |
(53) |
|
0,0000 |
|
0,0000 |
0,0809 |
0,0000 |
X2 |
0,9323 |
0,9873 |
|
0,2105 |
0,7750 |
|
(53) |
(53) |
|
(53) |
(53) |
|
0,0000 |
0,0000 |
|
0,1303 |
0,0000 |
X3 |
0,2757 |
0,2419 |
0,2105 |
|
-0,2968 |
|
(53) |
(53) |
(53) |
|
(53) |
|
0,0457 |
0,0809 |
0,1303 |
|
0,0309 |
X4 |
0,6647 |
0,7638 |
0,7750 |
-0,2968 |
|
|
(53) |
(53) |
(53) |
(53) |
|
|
0,0000 |
0,0000 |
0,0000 |
0,0309 |
|
Поиск и исключение аномальных наблюдений.
График «Outlier Plot» показывает, как далеко отстоят наблюдения от среднего значения показателя. Последовательно удаляем точки за границами плюс-минус 4 стандартных отклонения до тех пор, пока параметр P-Value для теста Граббса превысит 0,05 оставшиеся наблюдения с вероятностью 0,95 будут не аномальны.
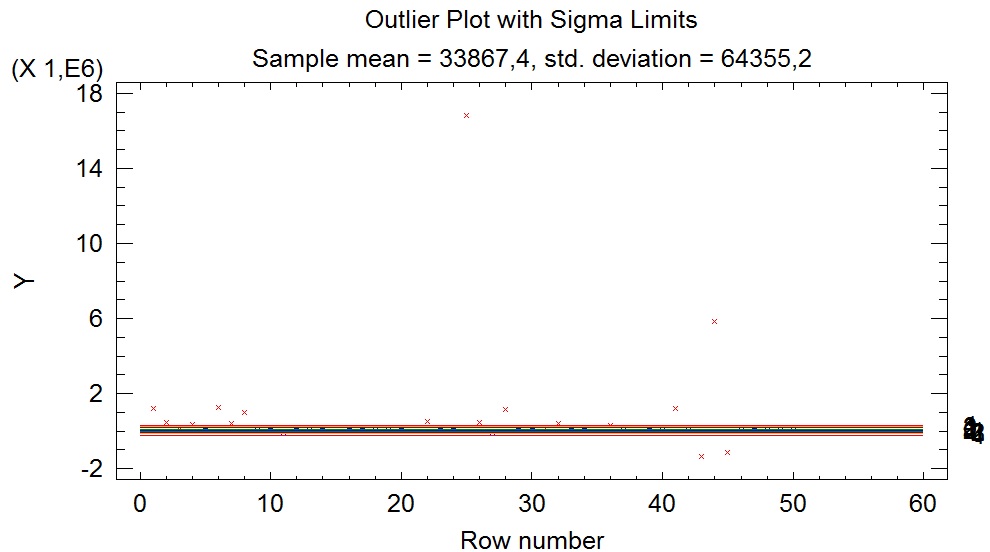
Рис. 1. Разброс наблюдений для Y (исключённые аномальные наблюдения отмечены красными крестиками)
После исключения 16 наблюдений по Y статистика теста Граббса 2,8789, а соответствующее значение P-Value=0,0608 > 0,05. Результат сохраним в виде переменной-флага SELECTED_Y.
Нормирование переменных.
Чтобы устранить влияние разных единиц измерения и облегчить интерпретацию моделей, нормируем значения переменных, разделив их на стандартные отклонения.
Хi_norm=Xi/δx
Наблюдения, признанные аномальными при расчете стандартного отклонения не учитываем.
Пронормируем переменные по следующим формулам:
Y_norm=SELECT(Y;SELECTED)/SD(SELECT(Y;SELECTED))
X1_norm= SELECT(X1;SELECTED)/SD(SELECT(X1;SELECTED))
X2_norm= SELECT(X2;SELECTED)/SD(SELECT(X2;SELECTED))
X3_norm= SELECT(X3;SELECTED)/SD(SELECT(X3;SELECTED))
X4_norm= SELECT(X4;SELECTED)/SD(SELECT(X4;SELECTED))
Результат сохраним в новых столбцах.
Обновим процедуру корреляционного анализа: посчитаем без учета аномальных наблюдений.
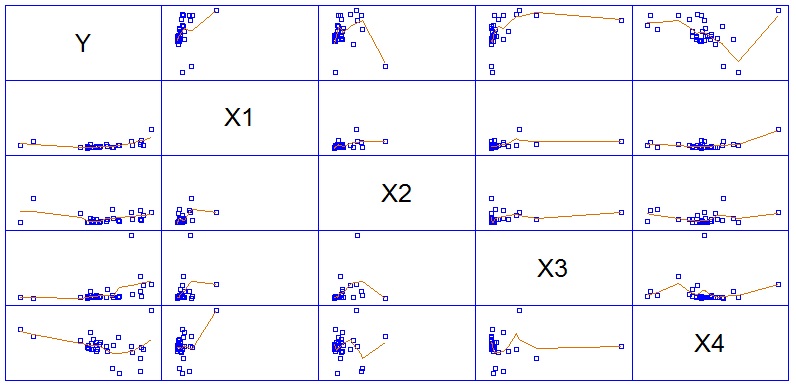
Рис. 2. Графики разброса показателей с линиями локально взвешенной регрессии после исключения аномальных наблюдений
Таблица 2. Корреляционная матрица переменных после исключения аномальных наблюдений
|
Y |
X1 |
X2 |
X3 |
X4 |
Y |
|
0,3866 |
0,0075 |
0,3966 |
-0,2800 |
|
|
(31) |
(31) |
(31) |
(31) |
|
|
0,0317 |
0,9682 |
0,0272 |
0,1271 |
X1 |
0,3866 |
|
0,5004 |
0,3563 |
0,4495 |
|
(31) |
|
(31) |
(31) |
(31) |
|
0,0317 |
|
0,0041 |
0,0492 |
0,0112 |
X2 |
0,0075 |
0,5004 |
|
0,2838 |
0,0377 |
|
(31) |
(31) |
|
(31) |
(31) |
|
0,9682 |
0,0041 |
|
0,1219 |
0,8405 |
X3 |
0,3966 |
0,3563 |
0,2838 |
|
0,0117 |
|
(31) |
(31) |
(31) |
|
(31) |
|
0,0272 |
0,0492 |
0,1219 |
|
0,9502 |
X4 |
-0,2800 |
0,4495 |
0,0377 |
0,0117 |
|
|
(31) |
(31) |
(31) |
(31) |
|
|
0,1271 |
0,0112 |
0,8405 |
0,9502 |
|
