Как возвести матрицу в квадрат?

Операция определена только для квадратных матриц – «два на два», «три на три» и т.д.

Возвести квадратную матрицу   в квадрат – это значит, умножить её саму на себя:

Пример 3

Возвести в квадрат матрицу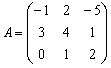 

Решение: пример рутинный, и чтобы извлечь максимальную пользу, давайте закрепим очень распространённый случай умножения двух матриц «три на три»:

Строки первой матрицы – это столы в ресторане, а цветные столбцы второй матрицы – официанты. Сначала столы обслуживает красный официант, затем зелёный официант, и под конец застолья – синий официант. Тааак, хватит прикалываться, он не голубой =)

Это действительно удобный мысленный приём, который можно использовать на практике – последовательно (слева направо) перебираем столбцы второй матрицы  и «пристраиваем» их к каждой строке первой матрицы.

Ответ: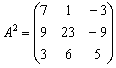 

Возведение матрицы в куб и более высокие степени разберём позже.

Немного о некоммутативности матричного умножения и единичной матрице

Материал, по меньшей мере, частично вам знаком. Для тех, кто не знает термина:  Коммутативность = Перестановочность.

Обычные числа переставлять можно:  , а матрицы в общем случае не перестановочны:  . Собственно, подробная иллюстрация с конкретными примерами уже была дана в статье Действия с матрицами.

Рассмотрим некоторые исключения из правила, которые потребуются для выполнения практических задач.

Если у квадратной матрицы   существует обратная матрица  , то их умножение коммутативно: 

Чтобы проверить, правильно ли найдена обратная матрица, нужно вычислить произведение   либо произведение   и убедиться в том, что получится единичная матрица  . Конкретные примеры можно посмотреть в статье Как найти обратную матрицу?

Единичной матрицей называется квадратная матрица, у которой на главной диагоналирасположены единицы, а остальные элементы равны нулю. Например:  ,  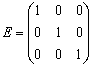 и т.д.

При этом справедливо следующее свойство: если произвольную матрицу   умножитьслева или справа на единичную матрицу подходящих размеров, то в результате получится исходная матрица:

Как видите, здесь также имеет место коммутативность матричного умножения.

Возьмём какую-нибудь матрицу, ну, скажем, матрицу из предыдущей задачи:  .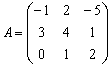

Желающие могут провести проверку и убедиться, что:

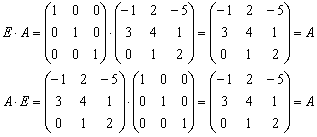
Единичная матрица для матриц – это аналог числовой единицы для чисел, что особенно хорошо видно из только что рассмотренных примеров.

Коммутативность числового множителя относительно умножения матриц

Для матриц   и действительного числа   справедливо следующее свойство:

То есть числовой множитель можно (и нужно) вынести вперёд, чтобы он «не мешал» умножить матрицы.

Примечание: вообще говоря, формулировка свойства неполная – «лямбду» можно разместить в любом месте между матрицами, хоть в конце. Правило остаётся справедливым, если перемножаются три либо бОльшее количество матриц.

Пример 4

Вычислить произведение

Решение: 

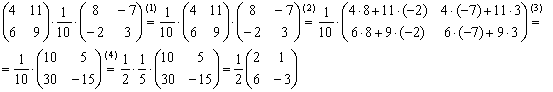
(1) Согласно свойству   перемещаем числовой множитель вперёд. Сами матрицы переставлять нельзя!

(2) – (3) Выполняем матричное умножение.

(4) Здесь можно поделить каждое число 10, но тогда среди элементов матрицы появятся десятичные дроби, что не есть хорошо. Однако замечаем, что все числа матрицы делятся на 5, поэтому умножаем каждый элемент на   .

Окончательный ответ лучше оставить в виде  , хотя, в принципе, годится и внесение дроби: 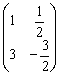 . На технических тонкостях умножения матрицы на число я подробно останавливался на уроке Действия с матрицами.

Ответ: 

Маленькая шарада для самостоятельного решения:

Пример 5

Вычислить  , если  

Решение и ответ в конце урока.

Какой технический приём важен в ходе решения подобных примеров? С числом разбираемся в последнюю очередь.

Прицепим к локомотиву ещё один вагон: