Как можно отблагодарить автора?

Некоторые свойства операций над матрицами. Матричные выражения

На базовых уроках Действия с матрицами, Как найти обратную матрицу? мы познакомились с понятием матрицы и основными операциями над матрицами. При этом основные акценты были подробно расставлены на технических приёмах вычисления, чтобы совершенно неподготовленный человек смог быстро научиться решать матрицы. Поэтому чайникам следует начать с первых двух статей и лягушатника с определителем матрицы. Из инструментальных средств рекомендую запастись матричным калькулятором, который позволит контролировать весь процесс решения и не допустить ошибок. Найти его можно, например, на складе математических формул и таблиц.

А сейчас последует продолжение темы, в котором мы рассмотрим не только новый материал, но и отработаем действия с матрицами.

Некоторые свойства операций над матрицами

Существует достаточно много свойств, которые касаются действий с матрицами, в той же Википедии можно полюбоваться стройными шеренгами соответствующих правил. Однако на практике многие свойства в известном смысле «мертвЫ», поскольку в ходе решения реальных задач используются лишь некоторые из них. Моя цель – рассмотреть прикладное применение свойств на конкретных примерах, и если вам необходима строгая теория, пожалуйста, воспользуйтесь другим источником информации.

Но сначала вернёмся к действиям с матрицами (к слову, в той статье мы уже неявно затронули ряд свойств). Начну с небольшого вопроса, который вызвал трудности у некоторых посетителей сайта:

Можно ли к матрице прибавить число?

Например:  . Ну, или наоборот: 

Нет. К матрице можно прибавить только другую матрицу, причём точно такого же размера.

Матрицу можно умножить на число. Но сложить их нельзя. Таковы правила игры.

Следует отметить, что допустимо сложение определителя матрицы с числом:

Результат вычисления определителя – число, а два числа суммируются без всяких проблем.

Вышесказанное, естественно, справедливо и для разности, ведь вычитание – это частный случай сложения.

Как на счёт того, чтобы плотно зависнуть у меня сегодня вечером? =) Практика показывает, что наибольшие трудности у студентов вызывает умножение матриц. Так наполним же кружки соответствующей информацией.

Повторим само правило. В статье Действия с матрицами я рассказал о том, какие матрицы можно умножать и привёл ряд наиболее распространённых примеров. Давайте рассмотрим операцию чуть подробнее и выделим два существенных пункта: 

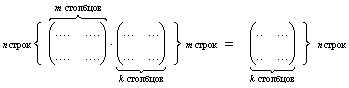
1) Смотрим на левую часть. Из первого урока нам известно, что матричное умножение возможно в том и только в том случае, если  количество столбцов первой матрицыравно количеству строк второй матрицы.

2) Смотрим на правую часть и обращаем внимание на размерность результата –СКОЛЬКО строк и столбцов должно быть у итоговой матрицы.

Пример 1

Умножить матрицы

Решение: произведение существует, причём итоговая матрица состоит из 1-ой строки и 2-х столбцов:

Ответ: 

Пример 2

Умножить матрицы

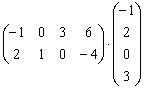
Это пример для самостоятельного решения.

Предложенные примеры не случайны. Они вроде бы просты, но у начинающих здесь нередко возникает путаница с размерами матрицы-результата. Поэтому читателям с небольшим опытом целесообразно переписать вышеприведённую формулу и особенно серьёзно отнестись к практическим примерам.

А по каким принципам составляются начинка (суммы произведений чисел), думаю, все уже поняли. Дополнительно возьмём на вооружение образную ассоциацию, которая поможет хорошо запомнить действие. Читаем следующий параграф: