
- •Действия с матрицами
- •Как можно отблагодарить автора?
- •Как вычислить определитель?
- •Как можно отблагодарить автора?
- •Свойства определителя. Понижение порядка определителя
- •Эффективные методы вычисления определителя
- •Определитель выгоднее раскрывать по той строке (столбцу), где:
- •Свойства определителя
- •При транспонировании матрицы величина её определителя не меняется
- •Если две строки (или два столбца) определителя поменять местами, то определитель сменит знак
- •Из строки (столбца) определителя можно вынести общий множитель
- •Если две строки (столбца) определителя пропорциональны (как частный случай – одинаковы), то данный определитель равен нулю
- •Определитель с нулевой строкой (столбцом) равен нулю
- •Какие свойства определителей полезно знать?
- •Понижение порядка определителя
- •К строке определителя можно прибавить другую строку, умноженную на ненулевое число. При этом величина определителя не изменится
- •К столбцу определителя можно прибавить другой столбец, умноженный на ненулевое число. При этом величина определителя не изменится
- •Как можно отблагодарить автора?
- •Как найти обратную матрицу?
- •Как можно отблагодарить автора?
- •Некоторые свойства операций над матрицами. Матричные выражения
- •Некоторые свойства операций над матрицами
- •Можно ли к матрице прибавить число?
- •Как возвести матрицу в квадрат?
- •Немного о некоммутативности матричного умножения и единичной матрице
- •Коммутативность числового множителя относительно умножения матриц
- •Как умножить три матрицы?
- •Как возвести матрицу в куб и более высокие степени?
- •Матричные выражения
- •Как можно отблагодарить автора?
- •Матричные уравнения. Примеры решений
- •Общие принципы решения матричных уравнений
- •Как решить матричное уравнение?
- •Как выполнить проверку?
- •Распространённый алгоритм решения матричного уравнения
- •Решение матричного уравнения вида
- •Решение матричного уравнения вида
- •Как можно отблагодарить автора?
- •Как решить систему линейных уравнений?
- •Решение системы линейных уравнений методом подстановки
- •Решение системы методом почленного сложения (вычитания) уравнений системы
- •Как можно отблагодарить автора?
- •Как решить систему линейных уравнений?
- •Решение системы линейных уравнений методом подстановки
- •Решение системы методом почленного сложения (вычитания) уравнений системы
- •Как можно отблагодарить автора?
- •Правило Крамера. Метод обратной матрицы
- •Решение системы по формулам Крамера
- •Решение системы с помощью обратной матрицы
- •Как можно отблагодарить автора?
- •Метод Гаусса (последовательного исключения неизвестных). Примеры решений для чайников
- •Как можно отблагодарить автора?
- •Решение систем линейных уравнений. Несовместные системы. Системы с общим решением. Частные решения
- •Как можно отблагодарить автора?
- •Как найти ранг матрицы?
- •Что такое ранг матрицы?
- •Как найти ранг матрицы с помощью миноров?
- •Алгоритм нахождения ранга матрицы с помощью миноров
- •Метод окаймляющих миноров
- •Как найти ранг матрицы с помощью метода Гаусса?
- •Какой метод использовать для нахождения ранга матрицы?
- •Как исследовать систему линейных уравнений на совместность?
- •Как можно отблагодарить автора?
- •Однородные системы линейных алгебраических уравнений
- •Что такое однородная система линейных уравнений?
- •Фундаментальная система решений однородной системы уравнений
- •Взаимосвязь решений неоднородной и соответствующей однородной системы уравнений
- •Как можно отблагодарить автора?
- •Метод Жордано-Гаусса. Как найти обратную матрицу с помощью элементарных преобразований?
- •Как найти обратную матрицу методом Гаусса?
- •Как можно отблагодарить автора?
- •Решение системы при различных способах выбора базиса
- •Как можно отблагодарить автора?
- •Собственные значения (числа) и собственные векторы. Примеры решений
- •Сколько у матрицы собственных чисел и собственных векторов?
- •Как найти собственные значения и собственные векторы матрицы?
- •Найти матрицу в базисе из собственных векторов
- •Как решать задачу в случае кратных собственных чисел?
- •Собственные векторы – это в точности векторы фундаментальной системы решений
- •Как можно отблагодарить автора?
- •Комплексные числа для чайников
- •Понятие комплексного числа
- •Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел
- •Тригонометрическая и показательная форма комплексного числа
- •Возведение комплексных чисел в степень
- •Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
- •Как можно отблагодарить автора?
Как решать задачу в случае кратных собственных чисел?
Общий алгоритм остаётся прежним, но здесь есть свои особенности, и некоторые участки решения целесообразно выдержать в более строгом академичном стиле:
Пример 6
Найти собственные числа и собственные
векторы
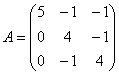
Решение: составим и решим
характеристическое уравнение:
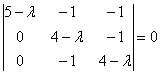
Конечно же, оприходуем сказочный первый
столбец:
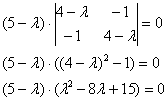
И, после разложения квадратного трёхчлена
на множители:
![]()
В результате получены собственные
числа ![]() ,
два из которых кратны.
,
два из которых кратны.
Найдем собственные векторы:
1) С одиноким солдатом ![]() разделаемся
по «упрощённой» схеме:
разделаемся
по «упрощённой» схеме:
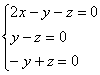
Из последних двух уравнений четко
просматривается равенство ![]() ,
которое, очевидно, следует подставить
в 1-ое уравнение системы:
,
которое, очевидно, следует подставить
в 1-ое уравнение системы:
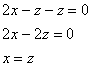
Лучшей комбинации не найти: ![]() Собственный
вектор:
Собственный
вектор: 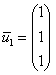
2-3) Теперь снимаем пару часовых. В случае
двух совпавших собственных чисел может
получиться либо два, либо
один собственный вектор. Невзирая
на кратность корней, подставим значение ![]() в
определитель
в
определитель 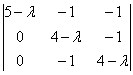 ,
который приносит нам следующую однородную
систему линейных уравнений:
,
который приносит нам следующую однородную
систему линейных уравнений:
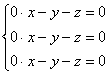
Собственные векторы – это в точности векторы фундаментальной системы решений
Собственно, на протяжении всего урока мы только и занимались тем, что находили векторы фундаментальной системы. Просто до поры до времени данный термин особо не требовался. Кстати, те ловкие студенты, которые в маскхалатах проскочили тему однородных уравнений, будут вынуждены вкурить её сейчас.
Запишем матрицу системы и с помощью
элементарных преобразований приведём
её к ступенчатому виду:
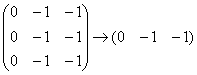
Единственное действие состояло в
удалении лишних строк. В результате
получена матрица «один на три» с
формальной «ступенькой» посередине.
–
базисная переменная, ![]() –
свободные переменные. Свободных
переменных две, следовательно, векторов
фундаментальной системы тоже два.
–
свободные переменные. Свободных
переменных две, следовательно, векторов
фундаментальной системы тоже два.
Выразим базисную переменную через
свободные переменные: ![]() .
Нулевой множитель перед «иксом» позволяет
принимать ему совершенно любые значения
(что хорошо видно и из системы уравнений).
.
Нулевой множитель перед «иксом» позволяет
принимать ему совершенно любые значения
(что хорошо видно и из системы уравнений).
В контексте данной задачи общее решение
удобнее записать не в строку, а в
столбец:
![]()
Паре ![]() соответствует
собственный вектор:
соответствует
собственный вектор: 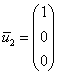 Паре
Паре ![]() соответствует
собственный вектор:
соответствует
собственный вектор: 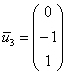
Примечание: искушенные
читатели могут подобрать данные векторы
и устно – просто анализируя систему
,
но тут нужны некоторые знания: переменных
– три, ранг
матрицы системы –
единица, значит, фундаментальная
система решений состоит
из 3 – 1 = 2 векторов. Впрочем, найдённые
векторы отлично просматриваются и без
этих знаний чисто на интуитивном уровне.
При этом даже «красивее» запишется
третий вектор: 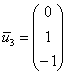 .
Однако предостерегаю, в другом примере
простого подбора может и не оказаться,
именно поэтому оговорка предназначена
для опытных людей. Кроме того, а почему
бы не взять в качестве третьего вектора,
скажем,
.
Однако предостерегаю, в другом примере
простого подбора может и не оказаться,
именно поэтому оговорка предназначена
для опытных людей. Кроме того, а почему
бы не взять в качестве третьего вектора,
скажем, 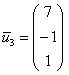 ?
Ведь его координаты тоже удовлетворяют
каждому уравнение системы, и
векторы
?
Ведь его координаты тоже удовлетворяют
каждому уравнение системы, и
векторы 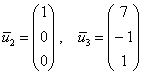 линейно
независимы. Такой вариант, в принципе,
годен, но «кривоват», поскольку «другой»
вектор
представляет
собой линейную комбинацию
линейно
независимы. Такой вариант, в принципе,
годен, но «кривоват», поскольку «другой»
вектор
представляет
собой линейную комбинацию 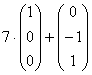 векторов
фундаментальной системы.
векторов
фундаментальной системы.
Ответ: собственные числа:
,
собственные векторы: 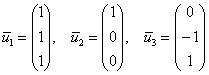
Аналогичный пример для самостоятельного решения:
Пример 7
Найти собственные числа и собственные
векторы
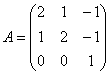
Примерный образец чистового оформления в конце урока.
Следует отметить, что и в 6-ом и в 7-ом примере получается тройка линейно независимых векторов, поэтому исходная матрица представима в каноническом виде . Но такая малина бывает далеко не во всех случаях:
Пример 8
Найти собственные числа и собственные
векторы матрицы
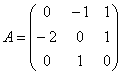
Решение: составим и решим
характеристическое уравнение:
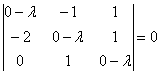
Определитель раскроем по первому
столбцу:
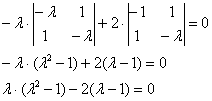
Дальнейшие упрощения проводим согласно
рассмотренной методике, избегая
многочлена 3-ей степени:
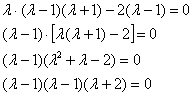
![]() –
собственные значения.
–
собственные значения.
Найдем собственные векторы:
1) С корнем
затруднений
не возникает:
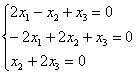
Не удивляйтесь, помимо комплекта в ходу также переменные – разницы тут никакой.
Из 3-го уравнения выразим ![]() –
подставим в 1-ое и 2-ое уравнения:
–
подставим в 1-ое и 2-ое уравнения:
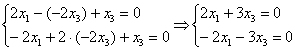
Из обоих уравнений следует: ![]()
Пусть ![]() ,
тогда:
,
тогда:
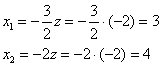
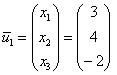
2-3) Для кратных значений ![]() получаем
систему
получаем
систему 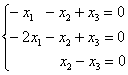 .
.
Запишем матрицу системы и с помощью
элементарных преобразований приведём
её к ступенчатому виду:
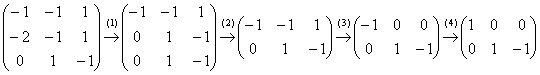
(1) Ко второй строке прибавили первую строку, умноженную на –2.
(2) Последние две строки одинаковы, одну из них удалили.
(3) Дальше пошла уместная доводка матрицы методом Жордано-Гаусса: к первой строке прибавили вторую строку.
(4) У первой строки сменили знак.
Переменные
–
базисные, переменная
–
свободная. Так как свободная переменная
одна, то фундаментальная система решений
состоит из одного вектора. И мы счастливые
наблюдатели случая, когда кратным
собственным числам соответствует
единственный собственный вектор.
Записываем в столбец общее решение
системы: ![]() ,
и, задавая свободной переменной
значение
,
получаем нашего героя:
,
и, задавая свободной переменной
значение
,
получаем нашего героя:
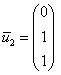
Ответ: собственные числа:
,
собственные векторы: 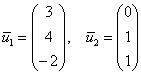 .
.
Исходную матрицу нельзя представить в базисе из собственных векторов по той простой причине, что такого базиса не существует – хоть трёхмерные векторы-столбцы и линейно независимы, но самих-то их всего лишь два. Недобор.
Шестое чувство мне подсказывает, что многие воодушевились на задание повышенной сложности:
Пример 9
Найти собственные числа и собственные
значения матрицы
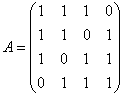 Можно
ли записать данную матрицу в канонической
форме?
Можно
ли записать данную матрицу в канонической
форме?
Не беда, если дело застопорилось, в психотерапевтических целях отложите тетрадь с решением на чёрный день. Когда заест скука – самое то =)
Успехов!
Решения и ответы:
Пример 2: Решение:
Найдем собственные значения. Составим
и решим характеристическое уравнение:
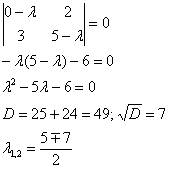
![]() –
собственные значения.
Найдем
собственные векторы:
1)
–
собственные значения.
Найдем
собственные векторы:
1) ![]()
![]() Пусть
Пусть
![]() –
собственный вектор.
2)
–
собственный вектор.
2) ![]()
![]() Пусть
Пусть ![]()
![]() –
собственный вектор.
Ответ:
собственные значения:
,
собственные векторы:
–
собственный вектор.
Ответ:
собственные значения:
,
собственные векторы: ![]() .
.
Пример 5: Решение:
сначала найдем собственные числа.
Составим и решим характеристическое
уравнение:
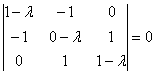 Определитель
раскроем по первой строке:
Определитель
раскроем по первой строке:

![]() –
собственные значения.
Найдем
собственные
векторы:
1)
–
собственные значения.
Найдем
собственные
векторы:
1)
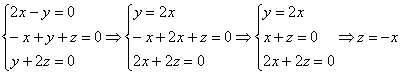 Пусть
Пусть ![]()
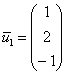 2)
2) ![]()
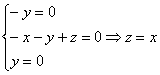 Пусть
Пусть ![]()
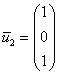 3)
3) ![]()
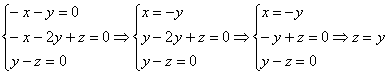 Пусть
Пусть ![]()
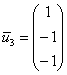 Ответ:
собственные векторы:
Ответ:
собственные векторы: 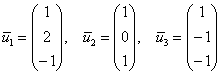
Пример 7: Решение:
составим и решим характеристическое
уравнение:

![]() –
собственные значения.
Найдем
собственные векторы:
1-2)
–
собственные значения.
Найдем
собственные векторы:
1-2) ![]()
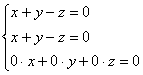 Запишем
матрицу системы и с помощью элементарных
преобразований приведём её к ступенчатому
виду:
Запишем
матрицу системы и с помощью элементарных
преобразований приведём её к ступенчатому
виду:
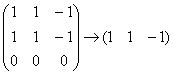 Выразим
базисную переменную
через
свободные переменные:
Выразим
базисную переменную
через
свободные переменные: ![]() и
запишем общее решение:
и
запишем общее решение: 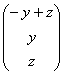 .
Найдём векторы фундаментальной системы,
которые в данной задаче являются
собственными векторами
матрицы:
Паре
.
Найдём векторы фундаментальной системы,
которые в данной задаче являются
собственными векторами
матрицы:
Паре ![]() соответствует
собственный вектор:
соответствует
собственный вектор: 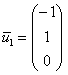 Паре
Паре ![]() соответствует
собственный вектор:
соответствует
собственный вектор: 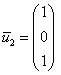 Примечание:
в качестве решения системы линейных
уравнений данного пункта напрашивается
тройка
Примечание:
в качестве решения системы линейных
уравнений данного пункта напрашивается
тройка ![]() ,
но столбец
,
но столбец ![]() линейно
выражается через векторы фундаментальной
системы. Использование такого и подобных
ему решений в качестве одного из
собственных векторов корректно, но
нестандартно.
3)
линейно
выражается через векторы фундаментальной
системы. Использование такого и подобных
ему решений в качестве одного из
собственных векторов корректно, но
нестандартно.
3) ![]()
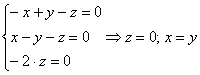 Пусть
Пусть ![]()
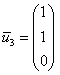 Ответ:
собственные числа:
,
собственные векторы:
Ответ:
собственные числа:
,
собственные векторы:
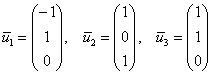
Пример 9: Решение:
Составим и решим характеристическое
уравнение:
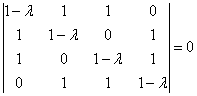
Определитель вычислим понижением
порядка. К третьей
строке прибавим вторую строку, умноженную
на –1. К четвёртой строке прибавим вторую
строку, умноженную на ![]() :
:
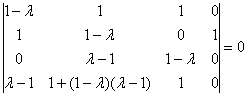 Разложим
определитель по 4-му столбцу:
Разложим
определитель по 4-му столбцу:
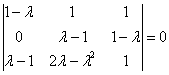 К
третьей строке прибавим первую
строку:
К
третьей строке прибавим первую
строку:
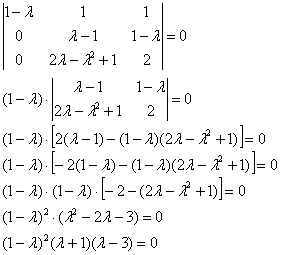
![]() Собственные
значения:
Собственные
значения: ![]()
Найдем собственные векторы:
1)
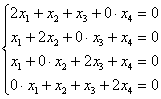 Запишем
матрицу системы и с помощью элементарных
преобразований приведём её к ступенчатому
виду:
Запишем
матрицу системы и с помощью элементарных
преобразований приведём её к ступенчатому
виду:
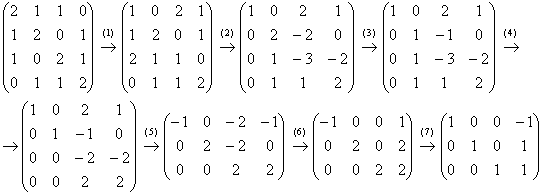 (1)
Первую и третью строку поменяли
местами.
(2) Ко 2-ой и 3-ей строкам
прибавили первую строку, умноженную на
–1 и –2 соответственно.
(3) Вторую
строку разделили на 2.
(4) К 3-ей и
4-ой строкам прибавили вторую строку,
умноженную на –1.
(5) Последние
две строки пропорциональны, третью
строку удалили. У первой строки сменили
знак, вторую строку умножили на 2.
(6)
К первой и второй строкам прибавили
третью строку.
(7) У первой строки
сменили знак, последние две строки
разделили на 2.
Выразив базисные
переменные через свободную, запишем
общее решение:
(1)
Первую и третью строку поменяли
местами.
(2) Ко 2-ой и 3-ей строкам
прибавили первую строку, умноженную на
–1 и –2 соответственно.
(3) Вторую
строку разделили на 2.
(4) К 3-ей и
4-ой строкам прибавили вторую строку,
умноженную на –1.
(5) Последние
две строки пропорциональны, третью
строку удалили. У первой строки сменили
знак, вторую строку умножили на 2.
(6)
К первой и второй строкам прибавили
третью строку.
(7) У первой строки
сменили знак, последние две строки
разделили на 2.
Выразив базисные
переменные через свободную, запишем
общее решение: ![]() .
Придаём свободной переменной значение
и
получаем собственный вектор
.
Придаём свободной переменной значение
и
получаем собственный вектор 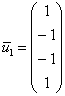 2-3)
2-3) ![]()
 Запишем
матрицу системы и с помощью элементарных
преобразований приведём её к ступенчатому
виду:
Запишем
матрицу системы и с помощью элементарных
преобразований приведём её к ступенчатому
виду:
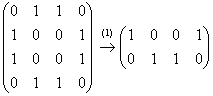 (1)
Первая и четвёртая строки одинаковы.
Вторая и третья строки одинаковы. Первую
и вторую строку удалили из матрицы.
Выразим
базисные переменные
через
свободные переменные
:
(1)
Первая и четвёртая строки одинаковы.
Вторая и третья строки одинаковы. Первую
и вторую строку удалили из матрицы.
Выразим
базисные переменные
через
свободные переменные
:
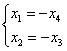 Таким
образом, общее решение:
Таким
образом, общее решение: ![]() .
Фундаментальная
система состоит из двух
векторов:
при
.
Фундаментальная
система состоит из двух
векторов:
при ![]() получаем
получаем 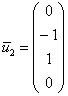 ;
при
получаем
;
при
получаем 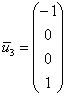 .
.
4)
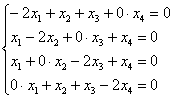 Запишем
матрицу системы и с помощью элементарных
преобразований приведём её к ступенчатому
виду:
Запишем
матрицу системы и с помощью элементарных
преобразований приведём её к ступенчатому
виду:
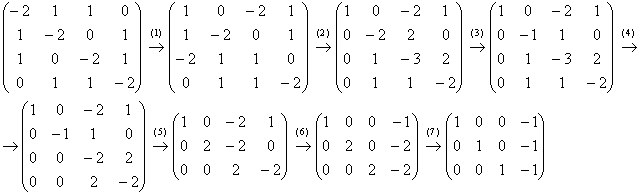 (1)
Первую и третью строку поменяли
местами.
(2) Ко 2-ой и 3-ей строкам
прибавили первую строку, умноженную на
–1 и 2 соответственно.
(3) Вторую
строку разделили на 2.
(4) К 3-ей и
4-ой строкам прибавили вторую строку.
(5)
Последние две строки пропорциональны,
третью строку удалили. Вторую строку
умножили на –2.
(6) К первой и
второй строкам прибавили третью
строку.
(7) Последние две строки
разделили на 2.
Общее решение:
(1)
Первую и третью строку поменяли
местами.
(2) Ко 2-ой и 3-ей строкам
прибавили первую строку, умноженную на
–1 и 2 соответственно.
(3) Вторую
строку разделили на 2.
(4) К 3-ей и
4-ой строкам прибавили вторую строку.
(5)
Последние две строки пропорциональны,
третью строку удалили. Вторую строку
умножили на –2.
(6) К первой и
второй строкам прибавили третью
строку.
(7) Последние две строки
разделили на 2.
Общее решение: ![]() .
Придаём свободной переменной значение
и
получаем собственный вектор
.
Придаём свободной переменной значение
и
получаем собственный вектор 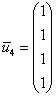 .
.
Ответ: собственные значения:
,
собственные векторы:
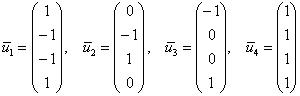 .
Перечисленные четыре четырехмерных
вектора линейно независимы, поэтому
матрицу можно записать в канонической
форме
.
Но лучше не надо =)
.
Перечисленные четыре четырехмерных
вектора линейно независимы, поэтому
матрицу можно записать в канонической
форме
.
Но лучше не надо =)
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
