Как найти собственные значения и собственные векторы матрицы?
Проведём исследование и получим алгоритм, по которому нужно решать данную задачу. Люди, которые не очень хорошо разбираются в математике (да и которые хорошо) обычно в страхе или отвращении захлопывают учебник, когда речь заходит о каком-либо доказательстве или выводе какой-нибудь формулы. Но это не тот случай – всё будет понятно даже полному чайнику:
Пример 1
Найти собственные числа и собственные векторы матрицы
Перед вами старая знакомая матрица, у которой я уже выдал одно собственное значение и один собственный вектор. Давайте научимся добывать их самостоятельно!
Обозначим через 
неизвестный
собственный вектор. Тогда матричное
уравнение 
запишется
следующим образом:
В левой части по обычному правилу
проведём матричное
умножение, в правой части
– внесём «лямбду»:
Две матрицы равны, если равны их
соответствующие элементы. Приравниваем
соответствующие элементы векторов-столбцов и
получаем однородную
систему линейных уравнений:
Перенесём всё налево:
В первом уравнении за скобки вынесем
«икс», во втором уравнении – «игрек»:
По определению, собственный вектор не
может быть нулевым 
,
поэтому нас не устраивает тривиальное
решение 
системы.
Следовательно, уравнения линейно
зависимы и определитель матрицы
системы равен нулю:
Это так называемое характеристическое уравнение матрицы , корни которого являются собственными числами данной матрицы.
Решение: на практике, как правило, не нужно расписывать подробный вывод формулы – вполне достаточно руководствоваться формальным алгоритмом.
Сначала найдём собственные значения
Составим характеристическое уравнение. Смотрим на исходную матрицу и записываем её определитель, вычитая при этом «лямбду» из чисел главной диагонали:
Раскроем определитель и решим квадратное
уравнение:
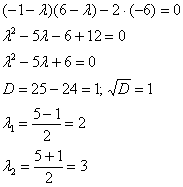
Таким образом, собственные значения: 
Желательно располагать их в порядке возрастания, хотя это не принципиально.
Теперь найдём собственные векторы
В данном примере получены различные собственные числа и каждому из них соответствует свой собственный вектор.
1) Рассмотрим собственное число
и
подставим значение 
в однородную
систему уравнений
:
Для записи системы целесообразно
запомнить формальный приём: мысленно
либо на черновике подставляем
в
определитель 
:
–
это и есть коэффициенты системы.
Из обоих уравнений следует:
Если в ходе решения выяснилось, что
линейной зависимости нет (т.е. получается
только тривиальное решение 
)
– ищите ошибку! Этот признак
касается всех задач рассматриваемого
типа.
Итак, в нашем распоряжении есть
выражение 
,
и координаты собственного вектора
определены
не однозначно. Стараемся подобрать
значение «игрек» так, чтобы первая
(«иксовая») координата собственного
вектора была целой, положительной
и минимальной.
Пусть 
,
тогда: 
Обязательно проверяем, что
частное решение
удовлетворяет
каждому уравнению системы:
Таким образом: 
2) Найдём второй собственный вектор. Для
этого мысленно либо на черновике
подставим 
в
определитель
и
запишем вторую однородную
систему:
Из обоих уравнений следует, что 
.
Положим 
,
тогда: 
В результате, собственный вектор: 
.
Повторим важные моменты решения: – полученная система непременно имеет общее решение (уравнения линейно зависимы);
– «игрек» подбираем таким образом, чтобы первая «иксовая» координата была целой, положительной и как можно меньше.
– проверяем, что частное решение 
удовлетворяет
каждому уравнению системы.
Ответ: собственные числа:
,
собственные векторы: 
.
Промежуточных «контрольных точек» было
вполне достаточно, поэтому проверка
равенств 
,
в принципе, дело излишнее.
В различных источниках информации
довольно часто собственные векторы
записывают не в столбцы, а в строки,
например: 
(и,
если честно, я сам привык записывать их
строками). Такой вариант вполне приемлем,
но всё-таки «идеологически правильнее»
использовать векторы-столбцы.
Возможно, решение показалась вам очень большим по объёму, но это только потому, что я очень подробно прокомментировал первый пример. На самом деле случай «два на два» – одно из самых простых и коротких заданий, которое только может встретиться в контрольной работе.
Пример 2
Найти собственные числа и собственные
векторы матрицы
Примерный образец чистового оформления в конце урока.
Иногда требуется выполнить дополнительное задание, а именно: