Как можно отблагодарить автора?

Собственные значения (числа) и собственные векторы. Примеры решений

Будь собой

Рассмотрим произвольную квадратную матрицу, например,  . И умножим данную матрицу справа на какой-нибудь подходящий столбец. Мне пришёл в голову вектор  :

Вроде ничего примечательного – умножили матрицу   на вектор-столбец   и получили другой вектор-столбец  . Обычная векторная жизнь. Но в обществе таких векторов существуют особые представители, которые обладают внутренним стержнем и не желают изменять себе в трудные минуты.

Умножим ту же матрицу на  :

На последнем шаге вынесли константу. Что произошло? В результате умножения матрицы    на вектор  , данный вектор птицей Феникс возродился с числовым коэффициентом  :

Определение: ненулевой вектор  , который при умножении на некоторую квадратную матрицу   превращается в самого же себя с числовым коэффициентом  , называетсясобственным вектором матрицы  . Число   называют собственным значением илисобственным числом данной матрицы. 

В первых абзацах статьи я выставил собственный вектор «главным действующим лицом», но на самом деле всё немного не так: говорят, что собственный вектор   соответствует собственному значению  . И, немного забегая вперёд, сообщу, что в практических заданиях сначала разыскиваются собственные значения и только потом собственные векторы.

Помимо собственных значений и собственных векторов матрицы, часто говорят о собственных значениях и собственных векторах линейного преобразования, заданного матрицей. В Википедии есть очень удачная геометрическая интерпретация понятия – на репродукции Джоконды синий вектор не меняется в результате перекоса плоскости, а значит, является собственным вектором данного линейного преобразования. Я скуп на внешние ссылки, но здесь не удержался, пожалуйста, сообщите, если данную иллюстрацию вдруг удалят.

Однако про геометрию немножко позабудем, поскольку сейчас в термины вектор, базис и др.вкладывается, прежде всего, алгебраический смысл. Собственные векторы и собственные значения используются во многих математических задачах, моделях, и сегодня мы освоим техническую сторону вопроса.

Сколько у матрицы собственных чисел и собственных векторов?

У квадратной матрицы размером   существует ровно   собственных значений, причём некоторые из них (или даже все) могут быть кратными (совпавшими).

Так, у демонстрационной квадратной матрицы   ровно два собственных значения, причём одно из них нам уже известно:  . Второе собственное число   гипотетически тоже может равняться «двойке» (но чаще всего, и здесь – в частности, собственные значения различны).

Могут ли собственные числа быть комплексными? Да, некоторые или все собственные значения могут быть комплексными. При этом алгоритм решения типовой задачи будет точно таким же. Однако на практике мне таких заданий не встречалось, поэтому в примерах данной статьи я ограничусь действительными собственными числами.

Что касается количества собственных векторов, то с ними ситуация занятнее. Любой вектор, который коллинеарен вектору   тоже будет собственным вектором. Действительно, если взять пропорциональные столбцы, скажем,   или  , то совсем несложно убедиться в равенствах:

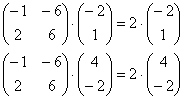
И с этой точки зрения у матрицы   бесконечно много собственных векторов. Но ходить туда-сюда по одной и той же тропинке скучно и уныло, поэтому под рассматриваемым вопросом всегда подразумевают количество линейно независимых (неколлинеарных) собственных векторов.

У квадратной матрицы размером   существует не более чем   собственных векторов.

Например, матрица «два на два» обладает, как максимум, двумя собственными векторами. Однако стойкий оловянный солдатик  может быть и в единственном экземпляре.

Каждому собственному значению соответствует хотя бы один собственный вектор, и из этого следует важное утверждение: если все собственные числа матрицы размером  различны, то она имеет ровно   собственных векторов. И в первых примерах мы как раз угостимся этим винегретом: