
- •Действия с матрицами
- •Как можно отблагодарить автора?
- •Как вычислить определитель?
- •Как можно отблагодарить автора?
- •Свойства определителя. Понижение порядка определителя
- •Эффективные методы вычисления определителя
- •Определитель выгоднее раскрывать по той строке (столбцу), где:
- •Свойства определителя
- •При транспонировании матрицы величина её определителя не меняется
- •Если две строки (или два столбца) определителя поменять местами, то определитель сменит знак
- •Из строки (столбца) определителя можно вынести общий множитель
- •Если две строки (столбца) определителя пропорциональны (как частный случай – одинаковы), то данный определитель равен нулю
- •Определитель с нулевой строкой (столбцом) равен нулю
- •Какие свойства определителей полезно знать?
- •Понижение порядка определителя
- •К строке определителя можно прибавить другую строку, умноженную на ненулевое число. При этом величина определителя не изменится
- •К столбцу определителя можно прибавить другой столбец, умноженный на ненулевое число. При этом величина определителя не изменится
- •Как можно отблагодарить автора?
- •Как найти обратную матрицу?
- •Как можно отблагодарить автора?
- •Некоторые свойства операций над матрицами. Матричные выражения
- •Некоторые свойства операций над матрицами
- •Можно ли к матрице прибавить число?
- •Как возвести матрицу в квадрат?
- •Немного о некоммутативности матричного умножения и единичной матрице
- •Коммутативность числового множителя относительно умножения матриц
- •Как умножить три матрицы?
- •Как возвести матрицу в куб и более высокие степени?
- •Матричные выражения
- •Как можно отблагодарить автора?
- •Матричные уравнения. Примеры решений
- •Общие принципы решения матричных уравнений
- •Как решить матричное уравнение?
- •Как выполнить проверку?
- •Распространённый алгоритм решения матричного уравнения
- •Решение матричного уравнения вида
- •Решение матричного уравнения вида
- •Как можно отблагодарить автора?
- •Как решить систему линейных уравнений?
- •Решение системы линейных уравнений методом подстановки
- •Решение системы методом почленного сложения (вычитания) уравнений системы
- •Как можно отблагодарить автора?
- •Как решить систему линейных уравнений?
- •Решение системы линейных уравнений методом подстановки
- •Решение системы методом почленного сложения (вычитания) уравнений системы
- •Как можно отблагодарить автора?
- •Правило Крамера. Метод обратной матрицы
- •Решение системы по формулам Крамера
- •Решение системы с помощью обратной матрицы
- •Как можно отблагодарить автора?
- •Метод Гаусса (последовательного исключения неизвестных). Примеры решений для чайников
- •Как можно отблагодарить автора?
- •Решение систем линейных уравнений. Несовместные системы. Системы с общим решением. Частные решения
- •Как можно отблагодарить автора?
- •Как найти ранг матрицы?
- •Что такое ранг матрицы?
- •Как найти ранг матрицы с помощью миноров?
- •Алгоритм нахождения ранга матрицы с помощью миноров
- •Метод окаймляющих миноров
- •Как найти ранг матрицы с помощью метода Гаусса?
- •Какой метод использовать для нахождения ранга матрицы?
- •Как исследовать систему линейных уравнений на совместность?
- •Как можно отблагодарить автора?
- •Однородные системы линейных алгебраических уравнений
- •Что такое однородная система линейных уравнений?
- •Фундаментальная система решений однородной системы уравнений
- •Взаимосвязь решений неоднородной и соответствующей однородной системы уравнений
- •Как можно отблагодарить автора?
- •Метод Жордано-Гаусса. Как найти обратную матрицу с помощью элементарных преобразований?
- •Как найти обратную матрицу методом Гаусса?
- •Как можно отблагодарить автора?
- •Решение системы при различных способах выбора базиса
- •Как можно отблагодарить автора?
- •Собственные значения (числа) и собственные векторы. Примеры решений
- •Сколько у матрицы собственных чисел и собственных векторов?
- •Как найти собственные значения и собственные векторы матрицы?
- •Найти матрицу в базисе из собственных векторов
- •Как решать задачу в случае кратных собственных чисел?
- •Собственные векторы – это в точности векторы фундаментальной системы решений
- •Как можно отблагодарить автора?
- •Комплексные числа для чайников
- •Понятие комплексного числа
- •Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел
- •Тригонометрическая и показательная форма комплексного числа
- •Возведение комплексных чисел в степень
- •Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями
- •Как можно отблагодарить автора?
Как можно отблагодарить автора?
|
Решение системы при различных способах выбора базиса
Представляю вашему вниманию заключительную статью по теме решения систем линейных уравнений. Материал предназначен для читателей, владеющих техникойэлементарных преобразований на среднем и высоком уровне. Чайникам рекомендую начать с урока метод Гаусса для чайников =), ну а остальным, как людям опытным, предлагаю непосредственно перейти к обсуждению задачи.
Рассмотрим некоторую систему
линейных уравнений с пятью неизвестными ![]() .
Можно было взять мЕньшее количество
переменных, можно бОльшее, суть не в
этом. Предположим, данная система
совместна и имеет общее
решение, в котором
базисные переменные
.
Можно было взять мЕньшее количество
переменных, можно бОльшее, суть не в
этом. Предположим, данная система
совместна и имеет общее
решение, в котором
базисные переменные ![]() выражаются
через свободные переменные
выражаются
через свободные переменные ![]() .
.
Ответим на вопрос, который зародился ещё на уроке Несовместные системы/системы с общим решением и окончательно созрел к занятию Метод Жордано-Гаусса:
А почему, собственно, в роли
базисных переменных должны выступать
именно
?
Нельзя ли в качестве базиса выбрать,
например, набор ![]() ?
Действительно, чем
хуже
«обычных»
?
?
Действительно, чем
хуже
«обычных»
?
Примечание: здесь и далее термин «базис» используется в общем алгебраическом смысле, пожалуйста, не ассоциируйте его с аффинным базисом плоскости или пространства.
В данном примере любые три переменные из списка могут выступать в качестве базисных переменных.
И сегодня мы узнаем, как находить решение системы в различных базисах:
Пример 1
Исследовать систему линейных
уравнений на совместность. В случае
совместности найти её решение при
различных способах выбора базиса.
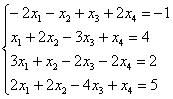
Решение: надо сказать, задачка не внушает оптимизма, велика вероятность, что система совместна и нам придётся ворочать базисы. Ещё бы – вряд ли в таком контексте условия студент отделается несовместностью системы или единственным решением =)
Но, так или иначе, первая часть предполагает исследование на совместность, которое проводится по типовой схеме с использованием теоремы Кронекера-Капелли. Спросите, зачем тут втиснулось исследование? Я взял пример из конкретной контрольной работы и решил не убирать первую часть (хотя мог бы), поскольку реализм на данном сайте ценится очень высоко.
Запишем расширенную матрицу
системы и с помощью элементарных
преобразований приведем ее к ступенчатому
виду:
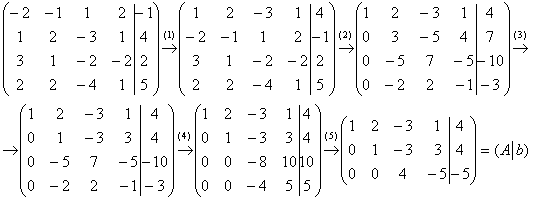
(1) Первую и вторую строки поменяли местами.
(2) Ко второй, третьей, четвертой строкам прибавили первую строку, умноженную на 2, –3 и –2 соответственно.
(3) Ко второй строке прибавили четвертую строку.
(4) К третьей и четвертой строкам прибавили вторую строку, умноженную на 5 и 2 соответственно.
(5) Третья и четвертая строки пропорциональны, третью строку удаляем. У последней строки меняем знак.
Если не очень понятны какие-нибудь моменты в преобразованиях, то, пожалуйста, отработайте метод Гаусса, благо, примеров я разобрал достаточно много.
Проверка системы на совместность оформляется по шаблону, рассмотренному в последнем параграфе статьи о ранге матрицы:
В результате элементарных преобразований получены эквивалентная исходным матрица системы и расширенная матрица системы .
Максимальный порядок ненулевого
минора матрицы системы равен 3, например 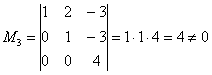 ,
следовательно,
.
,
следовательно,
.
По этой же причине .
Вывод: , значит, по теореме Кронекера-Капелли система совместна.
Элементарные образования приблизили нас к наиболее традиционному выбору: – базисные переменные; – свободная переменная.
Обратный ход метода Гаусса
работает без всяких чудес. Из третьего
уравнения:
![]() –
подставим во второе уравнение:
–
подставим во второе уравнение:
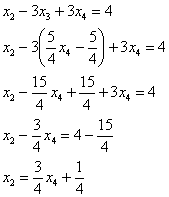
Подставим ![]() и
и ![]() в
первое уравнение:
в
первое уравнение:
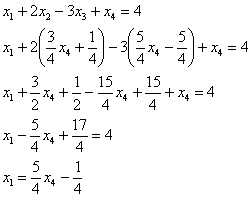
Общее решение системы в
базисе ![]() можно
записать в привычном виде
можно
записать в привычном виде ![]() ,
но в целях выполнения дальнейших действий
его удобнее оформить так:
,
но в целях выполнения дальнейших действий
его удобнее оформить так:
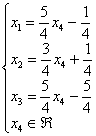
Запись ![]() обозначает,
что свободная переменная принимает
произвольные действительные значения,
порождая тем самым бесконечно много
частных решений.
обозначает,
что свободная переменная принимает
произвольные действительные значения,
порождая тем самым бесконечно много
частных решений.
Выполним стандартную проверку
– подставим результат в левую часть
каждого уравнения исходной системы:
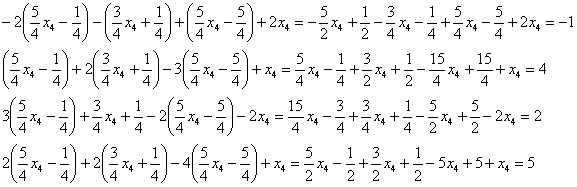
Получены правые части соответствующих уравнений, таким образом, общее решение найдено верно. Саму систему лучше переписать в тетрадь или распечатать – чтобы посматривать на неё в ходе последующих проверок.
По условию задачи требуется
найти решение системы при различных (читай
– при всех!)способах
выбора базисных переменных. Помимо
набора
возможны
следующие варианты:
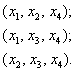 Других
сочетаний нет.
Других
сочетаний нет.
Не сказать, что задание сильно короткое, но с другой стороны в депрессию тоже не загонит. Начинаем путешествие:
В построенном базисе
переведём
неизвестную
в
разряд свободных
(
соответственно
станет базисной).
Переменная
содержится
в третьей строке полученного решения 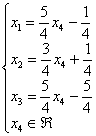 ,
поэтому нужно взять эту строку и
выразить
через
:
,
поэтому нужно взять эту строку и
выразить
через
:
![]()
Подставим ![]() в
оставшиеся выражения:
в
оставшиеся выражения:
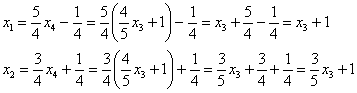
И, соблюдая порядок переменных,
запишем решение системы в базисе ![]()
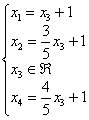
Для самоконтроля удостоверимся,
что в правых частях
находятся только свободные переменные
(в нашем случае
)
и константы.
Запись ![]() обозначает,
что свободная переменная принимает
произвольные действительные значения.
обозначает,
что свободная переменная принимает
произвольные действительные значения.
Общее решение также можно
оформить и в обычном виде:
![]() .
.
Понимаю, что неохота, но проходим таможенный контроль:
Проверка:
подставим найдённое решение в левую
часть каждого уравнения системы:
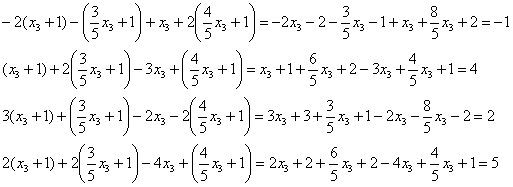
Получены соответствующие правые части уравнений, что и требовалось проверить.
Осуществим переход к следующему
базисному решению:
![]()
Поскольку переменная становится свободной, то из второй строчки текущего решения нужно выразить:
![]() –
и подставить в оставшиеся
выражения (первую и четвертую строки):
–
и подставить в оставшиеся
выражения (первую и четвертую строки):
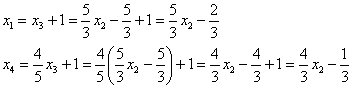
Таким образом, решение системы
в базисе ![]() :
:
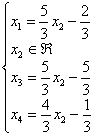
И снова окидываем результат взглядом – справа у нас должна находиться только свободная переменная и константы.
Проверка:
подставим результат в левую часть
каждого уравнения системы:
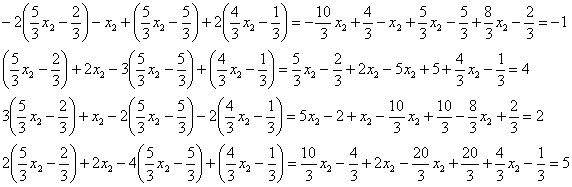 Получены
правые части соответствующих уравнений,
значит, решение найдено верно.
Получены
правые части соответствующих уравнений,
значит, решение найдено верно.
Каждый раз проверку, конечно, можете и не выполнять, но тут есть одно большое и жирноеНО В рассматриваемом задании часто ошибаются по невнимательности, поэтому настоятельно рекомендую проверять решение на каждом шаге – ведь если пропустить ошибку, всё остальное тоже будет неправильно. Ещё одним аргументом выступает сам естественнонаучный принцип: любое утверждение должно быть обосновано и/или доказано. Проверка реальна? Обязательно проверяем! Кстати, не такой плохой принцип и во многих жизненных ситуациях.
Завершая задание, найдём
решение системы в 4-ом базисе. Осуществим
переход:
![]()
Переменные и меняются ролями, а значит, из первой строки текущего решения следует выразить:
![]() –
подставим в оставшиеся
выражения (3-ю и 4-ю строки):
–
подставим в оставшиеся
выражения (3-ю и 4-ю строки):
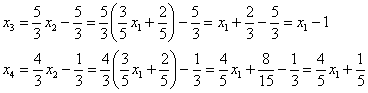
Записываем общее решение
системы в базисе ![]() :
:
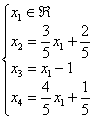
Проверка:
подставим найденное решение в левую
часть каждого уравнения системы:
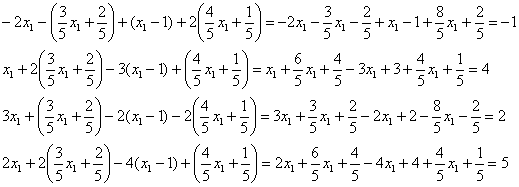
ОК.
Желающие могут замкнуть
кругосветный круиз переходом ![]() ,
получив тем самым первоначальное
решение.
,
получив тем самым первоначальное
решение.
В соответствии с условием задачи оформляем резюме:
Ответ:
система совместна, решение системы при
различных способах выбора базиса: 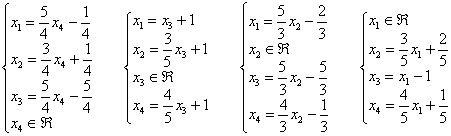
Если в системе с четырьмя
неизвестными ![]() базис
состоит из двух переменных (например,
базис
состоит из двух переменных (например, ![]() –
базисные переменные,
–
базисные переменные, ![]() –
свободные переменные), то переход от
одного решения к другому решению следует
осуществлять по тому же алгоритму, и он
даже запишется несколько компактнее,
чем в разобранной задаче. Правда, самих
базисов будет больше:
–
свободные переменные), то переход от
одного решения к другому решению следует
осуществлять по тому же алгоритму, и он
даже запишется несколько компактнее,
чем в разобранной задаче. Правда, самих
базисов будет больше:
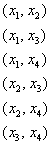
Количество базисов системы
с
переменными,
из
которых образуют базис, можно подсчитать
с помощью комбинаторной
формулы сочетаний ![]() .
.
Так, в условном примере начала урока с системой, содержащей пять неизвестных , три из которых образуют базис, будет уже 10 различных базисных решений.
Однако на практике я не встречал ни того, ни другого случая, видимо, связка 4 переменные – 3 базисные переменные является наиболее разумной с точки зрения объёма работы.
Такое тоже не встречалось,
но на всякий пожарный: что делать, если
по условию требуется найти конкретный
базис, например, решение
с базисными переменными ![]() и
свободной переменной
?
и
свободной переменной
?
При необходимости найти этот
базис сразу выручит
только метод
Жордано-Гаусса,
и ваша цель – привести расширенную
матрицу системы к виду 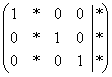 .
Если же автор задачи не торопит вас с
ответом, то кроме первого способа,
годится и второй, более длинный путь:
получаем «традиционное» решение и «без
посредников» осуществляем переход к
нужному базису:
.
Если же автор задачи не торопит вас с
ответом, то кроме первого способа,
годится и второй, более длинный путь:
получаем «традиционное» решение и «без
посредников» осуществляем переход к
нужному базису: ![]() .
.
Очевидно, что путешествовать от базиса к базису можно по разным маршрутам и решение следующей системы служит наглядной иллюстрацией данного факта:
Пример 2
Найти решение системы линейных
уравнений при различных способах выбора
базиса
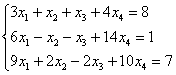
В образце первое базисное решение получено методом Жордано-Гаусса, который здесь более выгоден, чем обратный ход метода Гаусса.
В предложенной системе перебор
базисных решений проведён в следующем
порядке:
![]()
Более стандартна последовательность первого примера, но данный вопрос не принципиален, и для закрепления алгоритма рекомендую попытаться провести решение по альтернативному маршруту, который Птицей счастья завтрашнего дня появляется на экранах ваших мониторов.
Постарайтесь выполнить задание самостоятельно!
Решение: запишем
расширенную матрицу системы и с помощью
элементарных преобразований приведем
ее к ступенчатому виду:
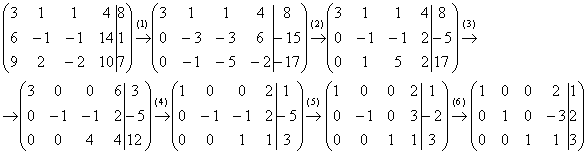 (1)
Ко второй и третьей строкам прибавили
первую строку, умноженную на –2 и –3
соответственно.
(2)
Вторую строку разделили на 3, у третьей
строки сменили знак.
(3)
К первой и третьей строкам прибавили
вторую строку.
(4)
Первую строку разделили на 3, третью
строку разделили на 4.
(5)
Ко второй строке прибавили третью
строку
(6)
У второй строки сменили знак.
Таким
образом, решение системы в
базисе
(1)
Ко второй и третьей строкам прибавили
первую строку, умноженную на –2 и –3
соответственно.
(2)
Вторую строку разделили на 3, у третьей
строки сменили знак.
(3)
К первой и третьей строкам прибавили
вторую строку.
(4)
Первую строку разделили на 3, третью
строку разделили на 4.
(5)
Ко второй строке прибавили третью
строку
(6)
У второй строки сменили знак.
Таким
образом, решение системы в
базисе ![]() :
:
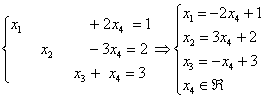 Проверка:
подставим данное решение в левую часть
каждого уравнения системы:
Проверка:
подставим данное решение в левую часть
каждого уравнения системы:
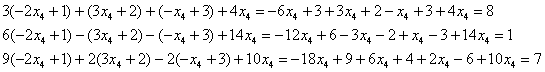 Получены
правые части соответствующих уравнений,
что и требовалось проверить.
Получены
правые части соответствующих уравнений,
что и требовалось проверить.
Найдем решение в базисе
.
Переменная
переходит
в разряд свободных, поэтому из первой
строки текущего решения выразим:
![]() –
подставим во вторую и третью строки:
–
подставим во вторую и третью строки:
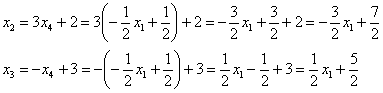 В
результате, решение в базисе
:
В
результате, решение в базисе
:
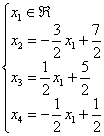 Проверка:
подставим данное решение в левую часть
каждого уравнения системы:
Проверка:
подставим данное решение в левую часть
каждого уравнения системы:
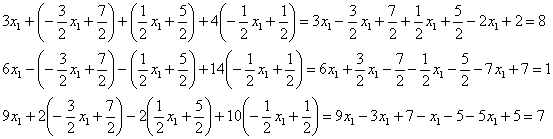 Получены
правые части соответствующих уравнений,
значит, решение найдено правильно.
Получены
правые части соответствующих уравнений,
значит, решение найдено правильно.
Осуществим переход к
базису
.
Переменная
перейдёт
в разряд свободных, поэтому из 2-ой строки
текущего решения выразим:
![]() –
подставим в третью и четвертую
строки:
–
подставим в третью и четвертую
строки:
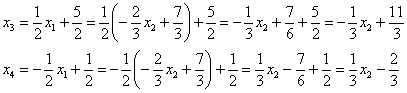 Таким
образом, решение в базисе
Таким
образом, решение в базисе ![]() :
:
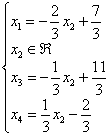 Проверка:
Подставим данное решение в левую часть
каждого уравнения системы:
Проверка:
Подставим данное решение в левую часть
каждого уравнения системы:
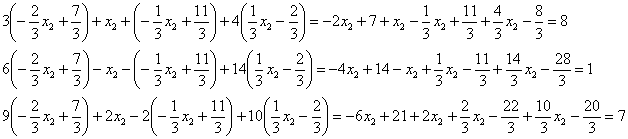 Найденное
решение удовлетворяет каждому уравнению
системы.
Найденное
решение удовлетворяет каждому уравнению
системы.
Перейдём к базису
.
Переменная
уходит
в разряд свободных, поэтому из 3-ей строки
текущего решения выразим:
![]() –
подставим в 1-ую и 4-ую строки:
–
подставим в 1-ую и 4-ую строки:
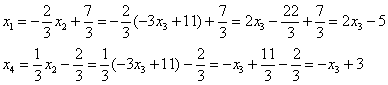 Решение
в базисе
:
Решение
в базисе
:
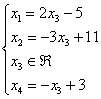 Проверка:
Подставим данное решение в левую часть
каждого уравнения системы:
Проверка:
Подставим данное решение в левую часть
каждого уравнения системы:
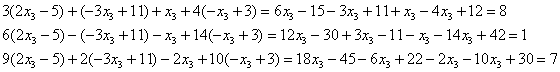 Полученное
решение удовлетворяет каждому
уравнению системы.
Полученное
решение удовлетворяет каждому
уравнению системы.
Ответ:
решение системы при различных способах
выбора базиса:
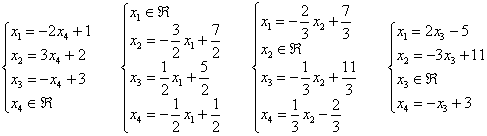
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
