Как найти обратную матрицу методом Гаусса?

Обычно условие формулируют сокращённо, но, по существу, здесь также работает алгоритм Жордано-Гаусса. Более простой метод нахождения обратной матрицы   для квадратной матрицы   мы давным-давно рассмотрели на соответствующем уроке, и суровой поздней осенью тёртые студенты осваивают мастерский способ решения.

Краткое содержание предстоящих действий таково: сначала следует записать квадратную матрицу   в тандеме с единичной матрицей:  . Затем с помощью элементарных преобразований необходимо получить единичную матрицу слева, при этом (не вдаваясь в теоретические подробности) справа нарисуется обратная матрица. Схематически решение выглядит следующим образом:

(Понятно, что обратная матрица должна существовать)

Не хочу показаться категоричным или придирчивым, но в подавляющем большинстве источников информации, которые я видел, данная задача рассмотрена крайне плохо – нужно обладать семью пядями во лбу и потратить массу времени/нервов на тяжёлое неуклюжее решение. За годы практики мне удалось отшлифовать, не скажу, что самую лучшую, но рациональную и достаточно лёгкую методику, которая доступна всем, кто владеет арифметическими действиями!

Демо-пример: найдём обратную матрицу для матрицы   с помощью элементарных преобразований. Для этого запишем её в одной упряжке с единичной матрицей:  .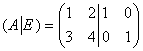

А теперь об одном принципиальном моменте. По цитате известного юмориста, для русского человека есть несколько градаций запрета: «запрещено», «строго запрещено» и «категорически запрещено». Так вот, в рассматриваемой задаче КАТЕГОРИЧЕСКИ ЗАПРЕЩЕНО переставлять строки. Если в ходе решения систем мы могли выполнять данное преобразование, то здесь его полное отсутствие заметно огранивает наши возможности.

Однако не всё так плохо:

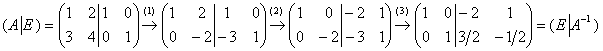
(1) Ко второй строке прибавили первую строку, умноженную на –3.

(2) К первой строке прибавили вторую строку.

(3) Вторую строку разделили на –2.

Таким образом:  . Желающие могут свериться с ответом первого примера урока Как найти обратную матрицу?

Но то была очередная заманивающая задачка – в действительности решение гораздо более длительно и кропотливо. Отработаем на реальных примерах алгоритм, который я считаю наиболее выгодным. Как правило, вам будет предложена матрица «три на три»:

Пример 4

Найти обратную матрицу с помощью элементарных преобразований

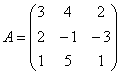
Решение: присоединяем единичную матрицу и думаем над первым действием. Чтобы получить слева вверху «единицу» хочется поменять местами первую и третью строки, однако беда в том, что ПЕРЕСТАВЛЯТЬ НИЧЕГО НЕЛЬЗЯ. Поэтому используем уже знакомый по предыдущему параграфу мотив: находим наименьшее общее кратное чисел первого столбца (3, 2 и 1): 6. В этой связи:

(1) Первую строку умножаем на –2, вторую строку умножаем на 3, третью строку – на 6:

(2) Ко 2-ой и 3-ей строкам прибавили первую строку.

(3) Первую строку разделили «обратно» на –2.  Третью строку разделили на 2.

(4) Что скажешь, тут немного повезло: к третьей строке прибавили вторую строку.

(5) У второй строки сменили знак, третью строку разделили на –3.

Первая половина пути пройдена.

Далее смотрим на числа третьего столбца (2, 13, 4) и находим их наименьшее общее кратное(НОК): 52. Существует строгий алгоритм нахождения НОК, но здесь обычно хватает подбора. Ничего страшного, если взять бОльшее число, которое делится и на 2, и на 13, и на 4, например, 104. Отличие будет в более громоздких вычислениях. 

Кстати, про вычисления. Для решения данной задачи совсем не зазорно вооружиться микрокалькулятором – числа фигурируют немалые, и будет очень обидно допустить вычислительную ошибку.

Итак, на нижнем этаже получаем –52, а на двух верхних 52. Для этого:

(6) Первую строку умножаем на 26, вторую строку умножаем на 4, третью строку – на –13:

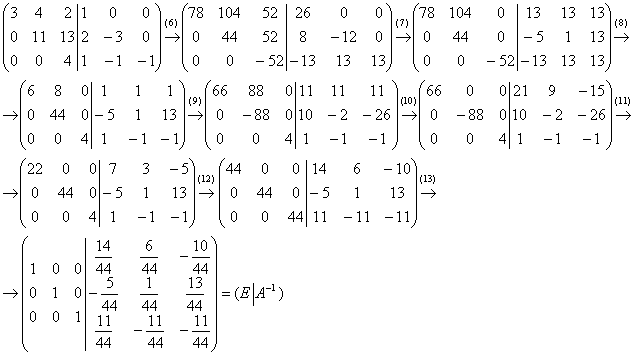
(7) К первой и второй строкам прибавили третью строку.

(8) Первую строку разделили на 13. Третью строку разделили «обратно» на –13.

(9) Наименьшее общее кратное ненулевых чисел второго столбца (8 и 44) равно 88. Первую строку умножили на 11, вторую строку умножили на –2.

(10) К первой строке прибавили вторую строку.

(11) Первую строку разделили на 3, вторую строку разделили «обратно» на –2.

(12) Теперь на главной диагонали левой матрицы целесообразно получитьнаименьшее общее кратное чисел диагонали (22, 44 и 4-х). Это число 44. Первую строку умножили на 2, третью строку умножили на 11.

(13) Каждую строку матрицы делим на 44. Данное действие выполняется в последнюю очередь!

Таким образом, обратная матрица:

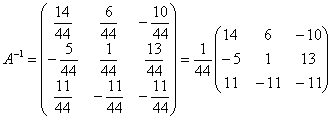
Внесение и вынесение  -ой, в принципе, лишние действия, но того требует протокол оформления задачи.

Ответ: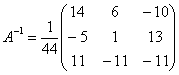 

Проверка выполняется по обычной схеме, рассмотренной на уроке об обратной матрице.

Продвинутые люди могут сократить и несколько видоизменить решение, но должен предупредить, отклонение от курса чревато повышенным риском допустить ошибку. По моему мнению, предложенная схема если и не самая, то одна из самых надёжных.

Аналогичное задание для самостоятельного решения:

Пример 5

Найти обратную матрицу методом Жордано-Гаусса.

Примерный образец оформления внизу страницы.

Иногда бывает удобно более короткое «модернистское» решение, которое заключается в следующем: на первом шаге всё как обычно:  .

На втором шаге накатанным приёмом (через НОК чисел 2-го столбца) организуются сразу два нуля во втором столбце: 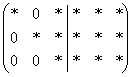 . Перед данным действием особенно трудно устоять, если во 2-ом столбце нарисовались одинаковые по модулю числа, например, «единицы».

И, наконец, на третьем шаге точно так же получаем нужные нули в третьем столбце:  .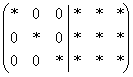

Живой пример авангарда можно посмотреть во втором задании урока о решении системы в различных базисах.

Что касается размерности, то в 98-99% случаев приходится разруливать матрицу «три на три». Пару раз в пятилетку попадается лайт-версия задачи с матрицей «два на два». Алгоритм, как вы догадываетесь, аналогичный. В самом тяжелом случае через НОК чисел 1-го столбца получаем ноль слева внизу, а затем с помощью НОК чисел 2-го столбца организуем ноль вверху данного столбца. Матрица «четыре на четыре» мне встречалась всего один раз – много-много лет назад в собственной вузовской контрольной. К слову, для неё использование метода Жордано-Гаусса куда менее трудозатратно, нежели обычное решение через алгебраические дополнения.

И заключительный совет – после таких примеров очень полезна гимнастика для глаз и какая-нибудь хорошая музыка для релаксации =)

Желаю успехов!

Решения и ответы:

Пример 3: Решение: запишем расширенную матрицу системы и с помощью элементарных преобразований получим базисное решение: 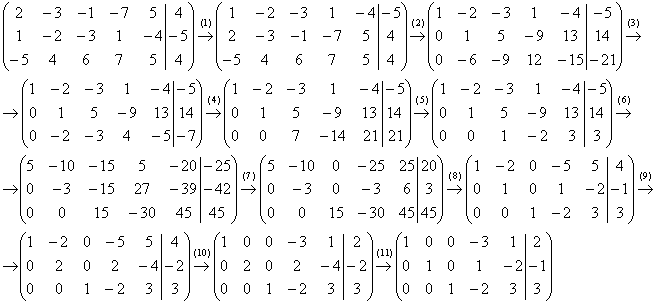  (1) Первую и вторую строки поменяли местами. (2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на 5. (3) Третью строку разделили на 3. (4) К третьей строке прибавили вторую строку, умноженную на 2. (5) Третью строку разделили на 7. (6) Наименьшее кратное чисел 3-го столбца (–3, 5, 1) равно 15-ти. Первую строку умножили на 5, вторую строку умножили на –3, третью строку умножили на 15. (7) К первой строке прибавили 3-ю строку. Ко второй строке прибавили 3-ю строку. (8) Первую строку разделили на 5, вторую строку разделили на –3, третью строку разделили на 15. (9) Наименьшее кратное ненулевых чисел 2-го столбца (–2 и 1) равно: 2. Вторую строку умножили на 2 (10) К первой строке прибавили вторую строку. (11) Вторую строку разделили на 2. Выразим базисные переменные   через свободные переменные  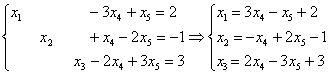: Ответ: общее решение: 

Пример 5: Решение: обратную матрицу найдём с помощью элементарных преобразований: 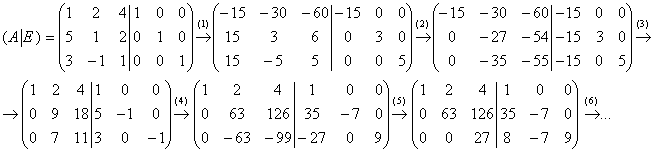(1) Первую строку умножили на –15, вторую строку умножили на 3, третью строку умножили на 5. (2) Ко 2-ой и 3-ей строкам прибавили первую строку. (3) Первую строку разделили на –15, вторую строку разделили на –3, третью строку разделили на –5. (4) Вторую строку умножили на 7, третью строку умножили на –9. (5) К третьей строке прибавили вторую строку. (6) Вторую строку разделили на 7. (7) Первую строку умножили на 27, вторую строку умножили на 6, третью строку умножили на –4. (8) К первой и второй строкам прибавили третью строку. (9) Третью строку разделили на –4. К первой строке прибавили вторую строку, умноженную на –1. (10) Вторую строку разделили на 2. (11) Каждую строку разделили на 27. В результате: 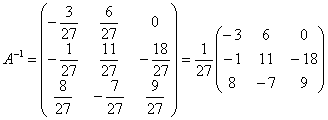 Ответ: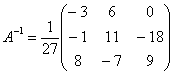 

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)